不同波形电压刺激下单晶LiNbO3薄膜忆阻器的电阻可塑性研究

颜 昊,潘忻强,,谢 琴,罗文博,,吴传贵,

(1.重庆邮电大学 光电工程学院,重庆 400065;2.电子科技大学重庆微电子产业技术研究院,重庆 401332;3.电子科技大学 电子科学与工程学院,四川 成都 611731)

随着物联网(IoT)的发展,传感器数量的急剧增加导致了数据量的急剧增加。在现有的架构之下,传感器采集到的所有原始数据都需要传送到中央计算单元进行处理和计算,无法在传感器端进行处理,这导致数据中心计算负荷大、数据传输延时长、能耗高[1]。近年来,人工智能被用于赋能物联网,形成人工智能物联网(AIoT),从提升物联网的智能化水平。但是这样,一方面,会进一步增加数据量;另一方面,人工智能中的神经网络计算对于算力提出了更高的要求。这导致数据量和中央计算单元的计算负荷进一步增大,从而进一步加剧了计算负荷大、传输时延长和能耗高的问题[2]。为了解决上述问题,亟需将计算任务下放到传感器端,通过在传感器端进行神经网络的边缘计算,以大幅降低中央计算单元的计算负荷和数据传输量。

传感器端的边缘计算面临能耗限制以及对高计算速度的要求[3]。然而,目前基于冯·诺依曼架构的计算硬件中,内存和计算是分离的,这导致了存储单元和计算单元之间数据不断移动带来的高能耗和延迟(又被称为冯·诺依曼瓶颈)[4],已无法满足传感器端神经网络边缘计算的要求。

忆阻器作为一种新型的器件,可将计算和存储统一到一个器件上,可以从根本上突破冯·诺依曼瓶颈[5]。并且,由忆阻单元构成的忆阻交叉阵列器件具有高度的计算并行性,可在一次运算中直接实现向量与矩阵的乘法运算,这是神经网络计算的基础[6]。此外,基于忆阻器件的神经网络计算是在模拟域,可直接对传感单元的模拟信号进行处理,无需数字信号与模拟信号之间的来回转换,消除了数模转换的硬件开销,进一步降低能耗和延迟[7]。因此,忆阻器被认为是传感器端神经网络边缘计算应用中最具潜力的核心器件。

在基于忆阻器的传感端神经网络边缘计算中,实现传感器与忆阻器的耦合至关重要。但是,不同的传感器端输出的信号具有不同的波形,例如,磁感应式传感器和霍尔式传感器输出方波信号,光电式传感器输出正弦波信号,位移传感器输出三角波信号。因此,需要研究不同信号刺激下的电阻可塑性。

在前期的研究中,研究人员基于单晶LiNbO3(LN)薄膜成功实现了忆阻器的制备[8]。后续针对其基本忆阻特性开展了研究,由于单晶LN 薄膜中没有传统多晶薄膜的晶界和晶粒,薄膜各处微观结构的一致性好,且可以为忆阻特性的调控提供良好的微观结构环境。通过忆阻特性调控研究,基于单晶LN 薄膜的忆阻器展现出高一致性、高稳定性、稳定的多级阻态以及良好的数据保持特性[9-10],这为忆阻器在神经网络计算中的应用奠定了基础。在此基础之上,已有研究人员进一步对其电阻可塑性进行了研究,但是研究中都是使用方波电压作为激励[11],尚未对不同波形电压刺激下的电阻可塑性进行研究。因此,本文针对忆阻器在传感端神经网络边缘计算中应用的需求,研究单晶LN 薄膜忆阻器在不同波形(三角波、正弦波、方波)电压刺激下的电阻可塑性。

本文主要研究了在不同波形电压的刺激下忆阻器件的电阻可塑性变化规律,并对其机制进行了分析。通过波形的优化抑制了电阻可塑性变化过程中的电阻突变现象。本文的研究工作将为未来基于忆阻器的传感端神经网络计算的实现搭桥铺路。

1 实验

本文采用离子注入-键合-剥离技术制备了基于单晶LN 薄膜的忆阻器件。具体过程如下: 先将He+注入到单晶LN 块材中的一定深度,并在注入后的单晶LN块材表面沉积Pt 金属。然后,通过等离子体增强化学气相沉积(PECVD)在Pt 电极表面和LN 衬底表面分别生长厚度为1 μm 的SiO2键合层。然后利用亲水性键合技术将已注入的单晶LN 块材与LN 衬底进行键合。注入的单晶LN 在300 ℃下退火3 h 后发生剥离,单晶LN 薄膜成功转移至LN 衬底上。再利用化学机械抛光技术对单晶LN 薄膜进行减薄和抛光。接着,采用低能Ar+轰击技术对单晶薄膜表面进行后处理,Ar+轰击时间为18 min,能量为100 eV,得到厚度约100 nm 的单晶LN 薄膜。最后,利用磁控溅射技术将直径为200 μm 的圆形Au 电极沉积在LN 薄膜表面。最终得到结构为Au/LN/Pt 的忆阻器,如图1 所示,其中Au 电极作为上电极,Pt 电极作为下电极。

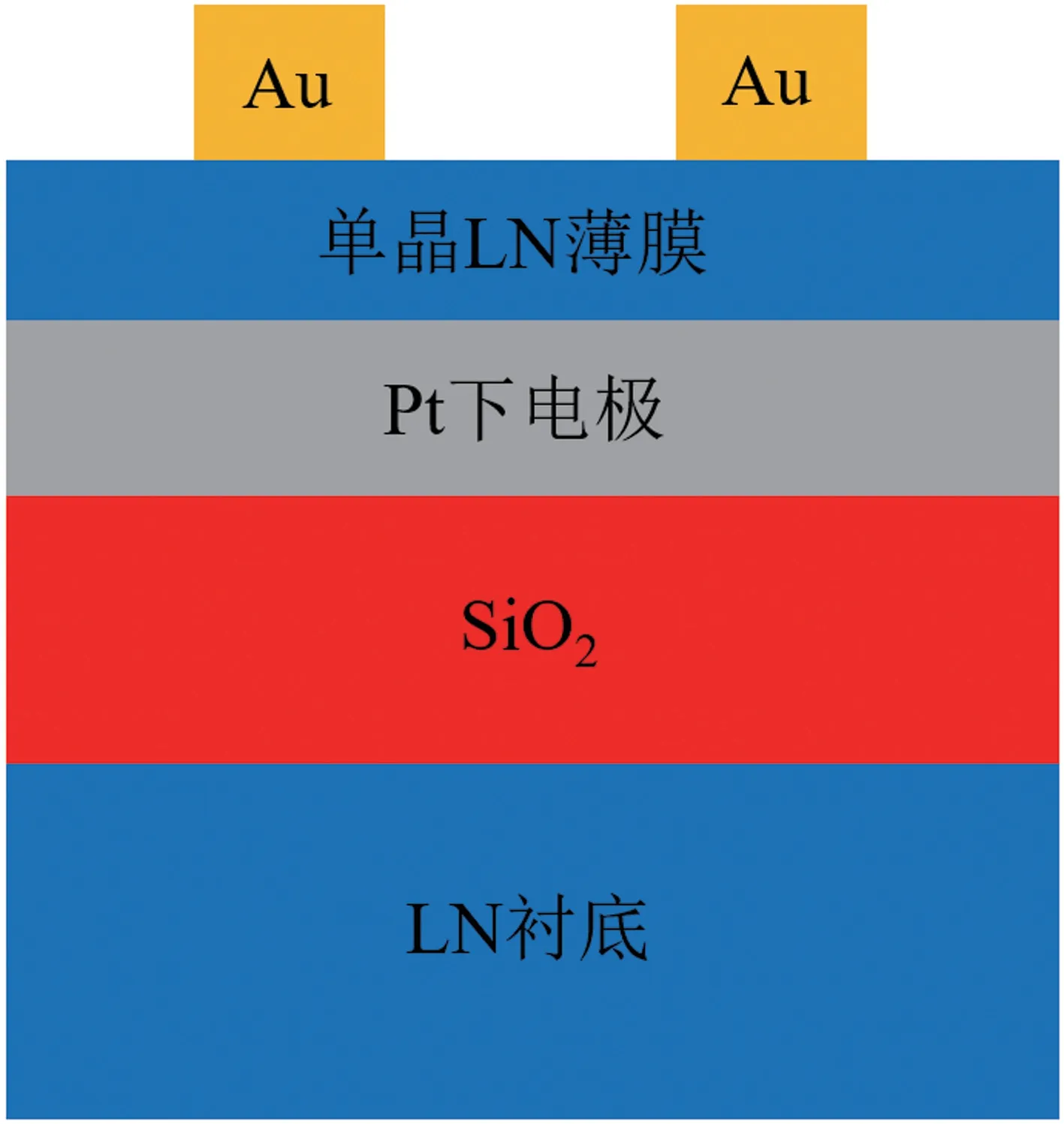
图1 基于单晶LN 薄膜的忆阻器结构示意图Fig.1 Schematic diagram of the memristor based on single-crystalline LiNbO3 thin film

本实验使用了Keithley 4200 源表和探针台搭建的测试平台,主要对包括电阻可塑性在内的忆阻器的电学特性进行了测试。测试时将样品上电极(Au 电极)与Keithley 4200 源表的正极相连,样品下电极(Pt 电极)与Keithley 4200 源表的负极相连并接地,如图2所示。

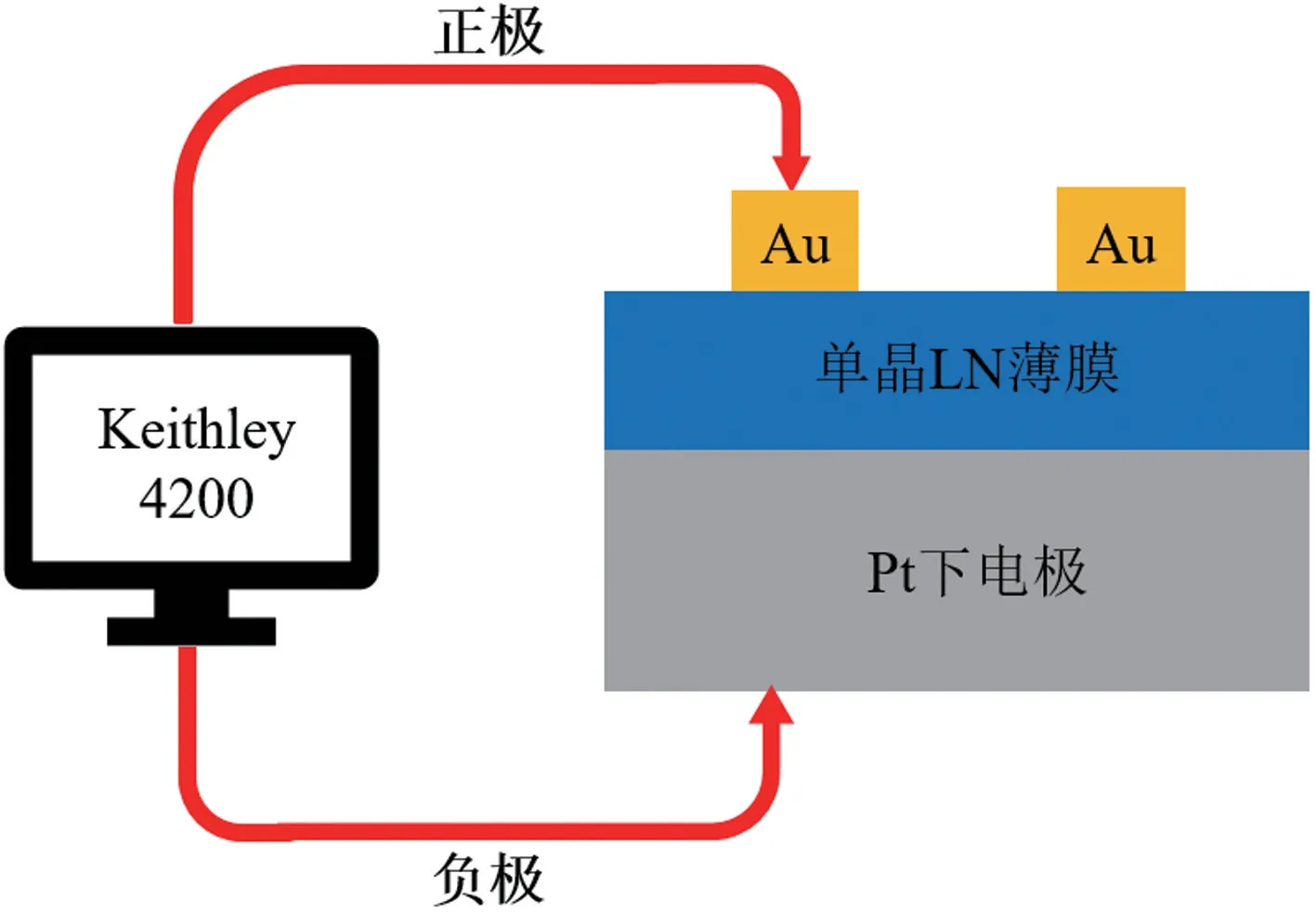
图2 测试平台连接示意图Fig.2 Schematic diagram of the test platform

实验中测试了三种电压刺激下的电阻可塑性,电压刺激分别是方波、正弦波和三角波,如图3 所示。为了控制变量,保持三种波形的电压幅值相同,且积分面积都相等。例如,设置三种波形幅值都为6 V,积分面积都为0.6 V·s,方波脉宽为100 ms,三角波脉宽为200 ms,正弦波脉宽为50π ms。测试电阻可塑性时,在增强过程(Potentiation Process)和抑制过程(Depression Process)中分别施加50 次写电压脉冲,在每一次写电压刺激后就采用幅值为1 V 的读电压去读取忆阻器的电导值。

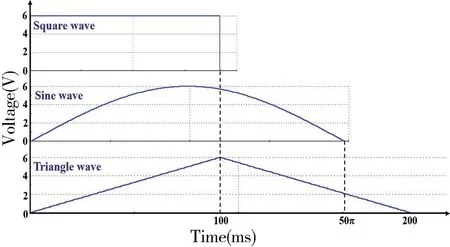
图3 三种电压的波形图Fig.3 The diagram of three kinds of voltage stimuli with different waveforms

2 结果与讨论

2.1 忆阻器件的基本忆阻特性

基于所制备的单晶LN 薄膜忆阻器进行研究,首先进行了I-V特性测试,测试时,限制电流设置为1×10-4A,扫描电压的施加顺序为: 0 V→正电压最大值→0 V→负电压最大值→0 V。如图4(a)所示,当施加电压在13 V 时,观察到了电形成过程,在电形成之后,测试了6 V 电压下的I-V特性曲线,可以观察到明显的阻变现象,具有较大的阻变窗口,如图4(b)所示。

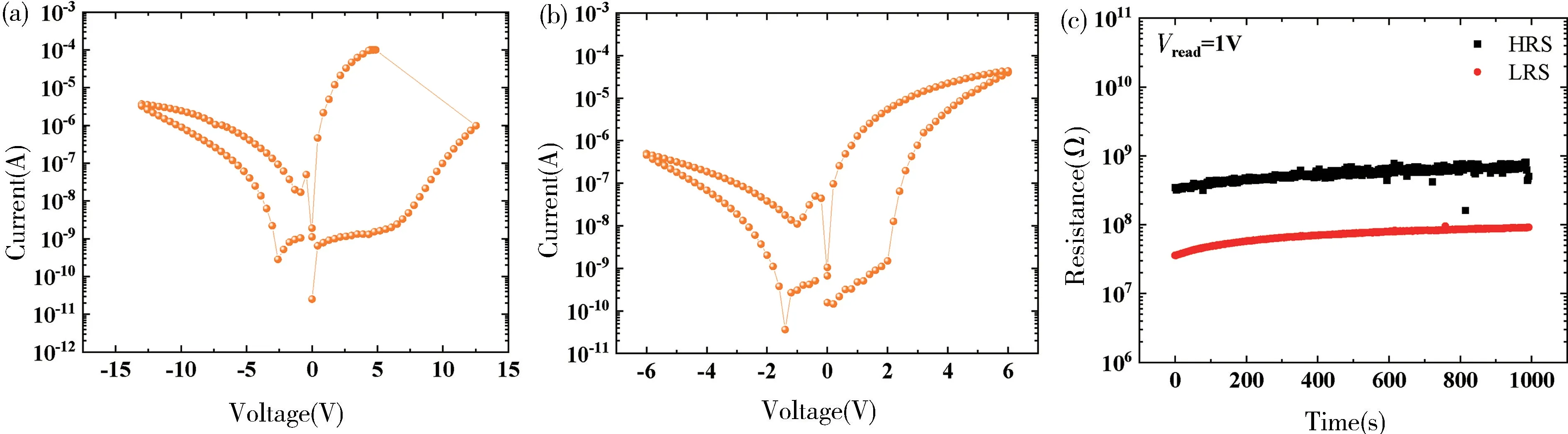
图4 电学特性。(a)电形成过程;(b)6 V 电压下的I-V 曲线;(c)高/低阻状态的数据保持特性Fig.4 Electrical characteristics.(a) Electro-forming process;(b) I-V curve at 6 V;(c) Retention characteristics of HRS/LRS

之后测试了数据保持特性,通过施加极性相反的写脉冲,将测试单元切换到高/低阻状态,然后每间隔2000 ms 施加一次读脉冲,读取其电阻状态,共读500次,测试结果如图4(c)所示,经过1000 s 后,电阻状态未发生明显变化,展现出良好的数据保持特性。

2.2 不同波形的电压刺激对电阻可塑性的影响规律

2.2.1 对电阻可塑性中增强过程的影响规律

在本部分的研究中,首先研究不同波形的电压刺激对电阻可塑性中增强过程的影响规律。在增强过程中,控制初始电导相同并均施加50 次脉冲刺激,在每一次脉冲刺激之后,采用幅值为1 V 的读电压读取电导状态。如图5 所示,在增强过程中,在三种不同波形的电压脉冲刺激下,忆阻器的电导均展现出缓慢渐变的特性。Burr 等在实验中证明,对于神经网络计算来说,温和渐变的响应(即忆阻器的电阻/电导在电压刺激下展现出缓慢渐变的特性)与陡峭的响应相比是有利的,可以让权重值更有规律地分布,进而为基于忆阻器件的神经网络计算提供较高的分类精度[12]。因此,该忆阻器件在三种不同波形的电压刺激下展现出的增强特性是有利于后续的神经网络计算的,有望满足传感器端神经网络边缘计算的要求。

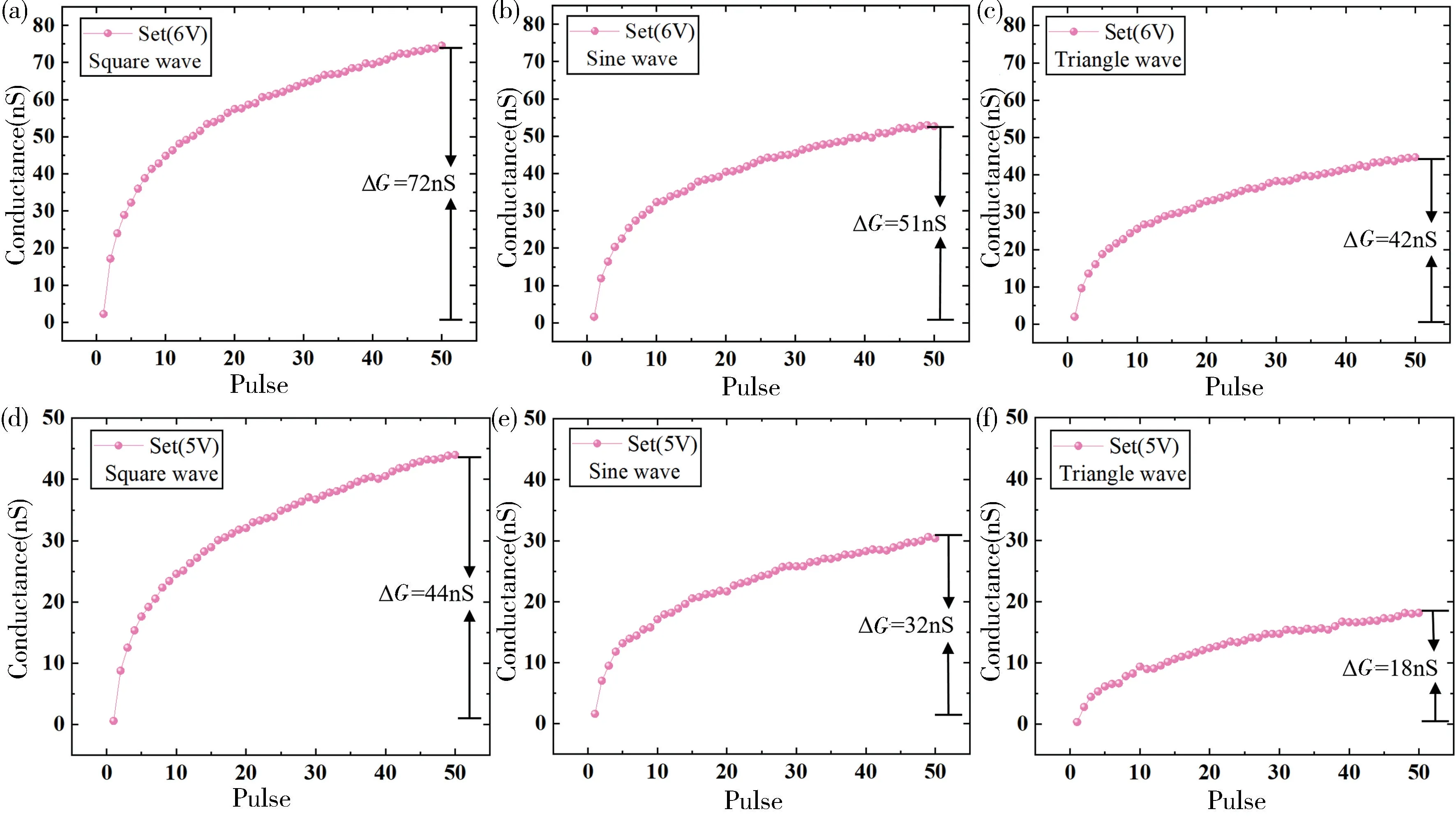
图5 不同电压刺激下的电阻可塑性。(a)幅值为6 V 的方波;(b)幅值为6 V 的正弦波;(c)幅值为6 V 的三角波;(d)幅值为5 V 的方波;(e)幅值为5 V 的正弦波;(f)幅值为5 V 的三角波Fig.5 Resistance plasticity under different voltage stimuli.(a) Square wave with amplitude of 6 V;(b) Sine wave with amplitude of 6 V;(c) Triangle wave with amplitude of 6 V;(d) Square wave with amplitude of 5 V;(e) Sine wave with amplitude of 5 V;(f) Triangle wave with amplitude of 5 V

当电压幅值均为6 V 时,测试结果如图5(a)～(c)所示。经过50 次刺激之后,方波刺激下电导变化幅度(ΔG)为72 nS,正弦波刺激下的ΔG为51 nS,三角波刺激下ΔG为42 nS。结果表明,方波刺激下电导变化幅度最大,正弦波其次,三角波刺激下的电导变化幅度最小。还测试了电压幅值均为5 V 时,三种波形电压刺激的影响如图5(d)～(f),仍然是方波刺激下的电导变化幅度最大,正弦波次之,三角波的最小。

为了厘清产生上述变化规律的原因,分别测试了50 次幅值为2,3,4 V 的方波刺激下的电导变化ΔG。如图6(a)～(c),幅值为2 V 和3 V 时,ΔG分别为1 nS 和2 nS,ΔG变化很小,几乎没有变化,而当幅值增大到4 V,ΔG为8 nS,变化较为显著,这说明只有超过一定幅度的电压脉冲才能够有效改变忆阻器的电导值,即存在一个可有效改变忆阻器电导的电压幅值的阈值。如图6(d)～(f),当上述电压幅值的阈值一定时,例如,设3 V 为阈值电压时,方波中超过阈值电压部分的占比为50%,正弦波中超过阈值电压部分的占比为34%,三角波中超过阈值电压部分的占比为25%,因此,幅值相同且积分面积相同的三种波形的电压刺激中,方波中高于阈值电压的部分占比最多,正弦波次之,三角波占比最少,这也就解释了为何方波刺激下的电导变化幅度最大,正弦波次之,三角波的最小[13]。

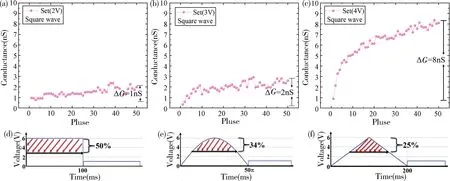
图6 不同幅值方波电压刺激下的电阻可塑性。(a)2 V;(b)3 V;(c)4 V;不同波形电压超过阈值部分的积分面积占比。(d)方波;(e)正弦波;(f)三角波Fig.6 Resistance plasticity under different square wave stimuli with different amplitudes.(a) 2 V;(b) 3 V;(c) 4 V;Proportion of integral area of different waveforms exceeding the threshold value.(d) Square wave;(e) Sine wave;(f) Triangle wave

之后,对图5(a)～(c)中所示的电阻可塑性的增强过程进行了线性度的分析。根据Tang 等提出的关于非线性度的计算方法[14],分别计算了这三种波形电压刺激下增强过程的非线性度值,其值分别为4.01,3.95 和3.42,如图7 所示。研究发现,线性度的高低主要取决于增强过程中初始阶段与后期电导变化的差异。由于初始阶段在三角波刺激下的电导变化最小,正弦波次之,方波最大,故在三角波刺激下,电导在初始阶段和后期的变化差异最小,正弦波次之,方波最大。因此,三角波刺激下的线性度最高,正弦波次之,方波的最低。而Chen 等的研究表明,基于非线性度值小于6 的忆阻器件,神经网络计算学习精度即可达到92%,所以本研究中三种波形电压刺激下的电阻可塑性线性度已经可以满足神经网络计算要求[15]。

由前文的分析可知,因为方波中高于阈值电压的部分占比最多,正弦波次之,三角波占比最少,所以在波形为方波的初次电压刺激下的电导变化最大,在波形为正弦波的初次电压刺激下的电导变化次之,在波形为三角波的初次电压刺激下的电导变化最小。因此,增强过程线性度由低至高依次为: 在方波刺激下的增强过程、在正弦波刺激下的增强过程、在三角波刺激下的增强过程。

2.2.2 对电阻可塑性中抑制过程的影响规律

在增强过程后,也对电阻可塑性中的抑制过程进行了测试,测试结果如图8(a)～(c)所示。由图可知,在波形分别为方波、正弦波、三角波的三组等幅电压刺激下,抑制过程的第一个点都呈现出电导突变现象,即在第一个电压刺激下,忆阻器就从低电阻状态跳变至较高的电阻状态,第一次电压刺激后的电导变化量在整个抑制过程中电导变化总量中的占比分别为91.2%,89.6%,87.5%。换言之,在抑制过程中,第一次刺激后,电导的变化量显著高于后续刺激下电导的变化量。

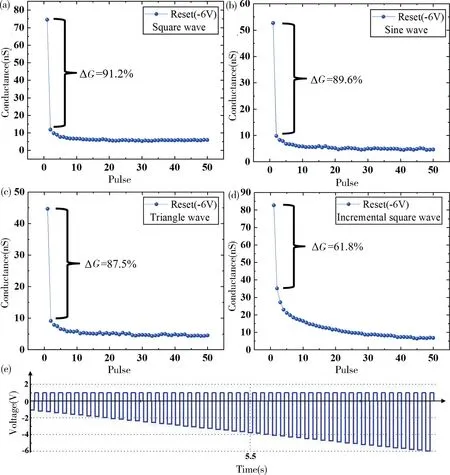
图8 抑制过程中不同电压刺激下的第一个点电导变化量占总变化量的比例。(a)方波;(b)正弦波;(c)三角波;(d)递增方波刺激下的抑制过程;(e)幅值从-1.1 V 逐渐增加到-6 V 的递增方波示意图Fig.8 The proportion of the conductivity change at the first point to the total change under different voltage stimuli during the depression process.(a)Square wave;(b) Sine wave;(c) Triangle wave;(d) The depression process under the square waves in (e);(e) Schematic diagram of the sequence of square wave with gradual increase amplitude from -1.1 V to -6 V

为了调节抑制过程的突变,就需要降低第一次刺激导致的电导变化量,同时增加后续电导刺激下的电导变化量。在Sridhar 等的研究中,证明了可通过改变电压脉冲组合调控电阻可塑性[16]。在本文中,通过调整电压刺激的幅值来实现,设计了另外一种电压方案,将50 次电压脉冲设置成递增的方波,从-1.1 V 增加到-6 V,每次增加-0.1 V,初始阶段通过降低幅值,减少初期的电导变化量,后续逐渐增加幅值,增加后续的电导变化量。每施加一次电压脉冲后,均采用幅值为1 V 的读电压读取电导值。如图8(d)～(e)所示,第一次电压刺激后的电导变化量占整个抑制过程中电导变化总量的61.8%,显著低于在之前的三个不同波形的电压刺激下抑制过程中第一次刺激后变化量的占比,电导突变现象得到明显改善,相应的整个电阻可塑性过程的对称性也显著提升,如图9 所示。

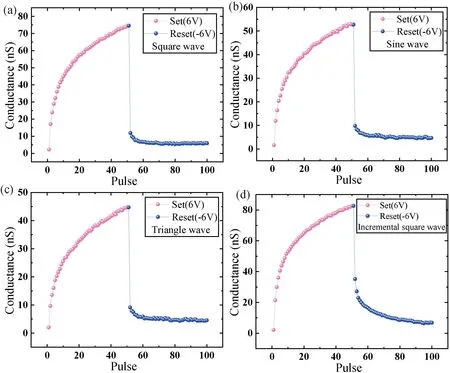
图9 不同电压波形刺激下的电阻可塑性曲线。(a)方波;(b)正弦波;(c)三角波;(d)幅值从-1.1 V 逐渐增加到-6 V 的递增方波Fig.9 Resistance plasticity curves under different voltage stimuli with different waveforms.(a) Square wave;(b) Sine wave;(c) Triangle wave;(d) The sequence of square wave with the gradual increase amplitude from -1.1 V to -6 V

3 结论

本文研究了单晶LN 薄膜忆阻器在方波、正弦波、三角波刺激下的电阻可塑性变化规律。在电压幅值和积分面积相同的情况下,在方波刺激下的电导变化幅度最大,正弦波次之,三角波最小,在电压刺激的幅值为6 V 时,方波刺激下电导变化可达72 nS,正弦波为51 nS,三角波为42 nS。经过测试与分析,在电压幅值和积分面积相同的条件下,电导变化幅度的差异主要由不同波形中超过特定阈值部分的面积的差异引起。在增强过程中,三角波刺激下的线性度最高,正弦波其次,方波最低。而在抑制过程中,在三种不同的波形电压刺激下,均观察到电阻突变的现象。基于对电阻突变过程原因的分析,本文通过使用幅值渐变电压脉冲序列来抑制该突变过程。本文的工作为未来实现传感器端基于忆阻器的神经网络边缘计算奠定了基础。