一人多机模式下考虑相似学习效应的车间调度问题
张维存 顾洪羽
河北工业大学经济管理学院,天津,300401
0 引言
随着我国制造装备的升级,刀具生产企业的多品种、小批量甚至定制化订单不断攀升,生产成本不断增加。刀具生产中,虽然自动化的生产设备扩大了工件的加工范围,提高了工件的质量和精度,但仍需工人进行装载、卸载、质量检查和状态监控等辅助作业,因此,“一人多机”的并行工作方式得到了重视和应用。
刀具的种类、材料、工装卡具,以及工人学习能力的差异影响着工人的作业效率和实际的作业调度。为贴近刀具企业“一人多机”的生产环境,笔者将传统车间调度中的工序作业细化为装载、卸载和机器加工,考虑作业相似性和工人学习效应使装卸时间具有的弹性,将有限的工人合理分配到装卸任务中,通过对装卸和加工任务的调度,尽可能缩短工时、节约人力、平衡工作负荷。
现实中,工人会因不断重复生产而积累工作经验的现象称为学习效应[1-2]。线性模型[1]反映了产品数量与时间的关系,但难以反映实际工时的变化趋势。为更真实地反映不同应用场景下的学习效应,后续又提出了Stanford-B模型、Plateau模型[3]、S-曲线模型和DeJong模型[4]。DeJong模型[4]认为学习效应一直存在于生产过程中,且随着生产作业的累积,学习曲线逐渐趋于稳定,符合本文研究的情景,为人-机的合理分配提供了依据。
近年来,学习效应在调度问题的求解中得到越来越多的关注。LI[5]研究了学习效应受随机处理时间和随机作业位置影响的单机调度问题,以最小化预期的总流程时间和最大化持续制造时间。JI等[4]建立了具有同质并行机的调度模型,应用DeJong学习效应函数计算了实际的作业时间。LIN[6]研究了具有可控加工时间和作业相关学习效应的并行机调度问题。LIANG等[7]基于对数处理时间的学习效应,解决了多目标流水车间调度问题。WANG等[8]研究了基于位置学习效应的置换流水车间调度问题。在更复杂的作业车间中,董君等[9]提出了受加工时间与加工位置共同影响的学习效应模型,并将其用于半导体晶圆制造的调度问题。ZOU等[10]研究了考虑学习效应的三机两阶段装配调度,在作业次数的基础上扩充了累计加工时间对学习效应的影响。胡金昌等[11]研究了基于工件位置学习效应的作业车间调度问题,并建立了多目标数学模型。显然,对复杂调度环境下学习效应的研究更贴近实际和便于应用,但更多研究还局限于单人单机的调度问题,多人多机且处理多工序的研究有待进一步扩充和完善。
在考虑学习效应的调度问题研究中,部分学者意识到相似的零件和工艺对各工序加工转换时间的影响。PARGAR等[12]研究了具有学习效应的混合流水车间调度问题,将工人能力的提高建模为重复类似任务的模型,通过相似工具共享和相似工序紧邻缩短转换时间。CHENG等[13]研究了位置加权学习效应下的调度问题,工人通过处理一组类似作业来获得工作经验、提升学习能力,进而得到更好的调度结果。此类研究更多关注作业相似对加工转换时间的影响,忽略了对装卸作业时间的影响。
在多目标优化问题中,随着目标数的增加,Pareto解的数量呈指数增长,为求解算法的选择和解集的维护增加了巨大的压力。目前,国内外学者对连续多目标优化算法进行了大量研究。CAI等[14]给出了基于网格加权和的支配关系,并将其用于Pareto解的局部搜索,对非支配解的筛选获得了明显效果。KHALILPOURAZARI等[15]提出了多目标随机分形搜索(MOSFS)方法,并利用外部档案、优势规则和网格机制,精确逼近真正的Pareto锋面。虽然离散多目标问题在实践中随处可见,但由于离散多目标优化问题的可行域是断开或割裂的,因此算法难以实现。构建近似Pareto前沿具有挑战性,实验效果难以验证,对其研究也相对较少。YU等[16]提出一种基于离散的通用多目标粒子群优化方法,采用分解策略,根据一组权向量将问题转化为多个单目标子问题。MANSON等[17]将高斯过程作为代理,结合基于高斯相似性的距离度量,提出一种能有效处理连续变量和离散变量的多目标算法。离散多目标优化算法存在计算量大、结构重分析次数多、不同量纲目标值协调难、搜索效率偏低等问题,所求解集的多样性难以保证。
综上,“一人多机”生产模式下考虑学习效应的作业车间调度问题,及该模式下相似学习效应对装卸作业时间的影响没有得到充分研究,同时也缺少相应高效的离散多目标求解算法。本文在“一人多机”生产模式下,考虑作业相似性和学习效应对装卸时间的影响,满足资源独占、工艺和作业顺序约束,体现工人多机作业特征,构建了多目标调度模型。采用两阶段解码方式,并利用改进的N6邻域搜索和启发式规则高效生成多目标的非支配调度方案。设计了基于网格筛选外部档案的遗传算法(grid filter external archive genetic algorithm,GFEAGA),利用网格技术对外部档案中的非支配解进行评价和选择,促进生成多样化的非支配解。
1 数学模型的建立
1.1 问题描述
“一人多机”模式下,考虑相似学习效应的作业车间调度问题可描述为:工件Ji(i∈{1,2,…,n})的m个工序分别在m台不同的自动化设备上加工,Oij(j∈{1,2,…,m})为工件i的第j个工序。每道工序依次可分为三个作业(装载、加工、卸载),并由设备k(k=1,2,...,m)完成。每个装卸作业需在w个工人中选择一人执行。不同的装卸作业具有相似性,且工人具备不同的学习能力,因此,执行装卸作业的实际时间有所不同。工人可在装卸作业(设备)之间自由行走。调度过程可描述为:考虑工人在设备间的行走时间和学习效应,选择装卸执行人员,并安排工人和设备执行装卸及加工作业的次序,使每道工序完成装载、加工、卸载;在满足生产约束的条件下,实现最大完工时间、工人总负荷、工人最大负荷和工人数量的最小化。模型中所涉及的参数符号定义如表1所示,涉及的变量符号定义如表2所示。

表1 参数符号定义

表2 变量符号定义
假设:①工人和设备同时只能处理一个工件;②不考虑搬运时间;③不考虑设备故障;④加工过程不允许中断;⑤工件间无优先级;⑥所有工人和设备零时刻可用;⑦设备缓存区足够大。
1.2 模型建立
模型中决策变量符号定义如表3所示。

表3 决策变量符号定义
DeJong函数[4]在设定学习效应模型时考虑了自动化程度M,DeJong的学习曲线模型为

(1)
实际生产中,工人的学习效应受主观因素和客观因素的影响。主观因素表现为工作经验、学习能力等,客观因素表现为作业相似性、现场秩序、作业指导等。调度问题中,现场秩序和作业指导等属于背景因素,不可调度或改变;工人的学习能力差异和作业相似性可通过工人选派和作业次序调整进行优化,这样可使调度方案更加贴合实际生产。因此,本文在DeJong学习曲线模型的基础上进行改进。改进后的学习曲线模型

(2)
既能体现工人学习效应,又能体现作业相似性对作业时间的影响。所有作业均相同即θijτ,hgρ=1时,则式(2)转换为式(1);当所有作业均不同即θijτ,hgρ=0时,则式(2)退化为Rijτ=tijτ。如图1所示,改进后的学习曲线在原DeJong学习曲线上方,且作业相似性越高,改进曲线越贴近原学习曲线。

图1 学习曲线模型对比
据此建立本研究模型如下:
(1)目标函数为
F1=min(maxEij3)
(3)
(4)

ya,ijτ,hgρvijτ,hgρ))
(5)
F4=minw
(6)
(2)约束条件为
(7)
Eijτ=Sijτ+Rijττ=1,2,3
(8)

(9)
λa,hgρ=λa,ijτ+∑xa,ijτxa,hgρya,ijτ,hgρ
(10)
i=1,2,…,nj=1,2,…,mτ=1,3
Shg1≥max(xa,qpρxa,hg1ya,qpρ,hg1(Eqpρ+vqpρ,hg1),
Eh(g-1)3,zij3, hg1Eij3)ρ=1,3
(11)
Sij2≥Eij1
(12)
Shg3≥max(Ehg2,ya,qpτ,hg3(Eqpρ+vqpρ,hg3))ρ=1,3
(13)
模型中,式(3)~式(6)分别表示最大完工时间、工人总负荷、最大工人负荷和作业人数;式(7)表示每项装卸作业仅由一人执行;式(8)表示装卸及加工作业的开始与结束时间的关系;式(9)表示工人实际装卸时间与标准时间的关系;式(10)表示工人a执行到作业ijτ时累计的作业数量;式(11)~式(13)分别表示装载、加工和卸载作业的开始时间计算关系。
2 算法设计
2.1 问题与算法分析
本研究将每个工序细分为装载、加工和卸载三项作业,需要选择装卸作业的执行人员,并对装卸及加工作业进行排序。由于设备的独占性,即设备只能同时处理单个工件的装载、加工、卸载,因此,可将工件的装载、加工、卸载视为一个整体,在设备上进行排产。本文采用两阶段的求解策略:第一阶段,将工序的装载、加工、卸载作一个整体进行排产,通过邻域搜索获得初始调度方案集;第二阶段,在初始调度方案基础上,对装载和卸载作业进行人员选派,形成完整调度方案。
2.2 个体编码与进化操作
2.2.1个体编码
采用两段式编码方法:前段编码由一个基因构成,代表决策变量w的取值;后段编码采用基于工序编码方式,编码长度为mn(代表所有工序编号),个体总编码长度为mn+1。
如图2所示:首位3表示由3个工人参与作业分配,后段2×4个基因表示工序,工件J1、J2分别用数字1和2表示。后段编码21221112中,第2次出现的数字1表示工件J1第2道工序即O12。

图2 两段式编码方式
根据基因位的工件号及编码规则,可以推出该工序的装卸及加工作业编号。解码过程中,通过作业编号并关联其加工信息,可对整个染色体进行解码。
2.2.2进化操作
为提高求解质量,除针对前段基因采用等位交叉及随机变异外,针对后段编码,通过实验选取了5种比较有效的交叉算子:基于顺序的交叉(order-based crossover,OBX)、基于位置的交叉(position-based crossover,PBX)、次序交叉(order crossover,OX)、集合分割的交叉(set-partition crossover,SPX)、优先操作交叉(precedence operation crossover,POX)。选取3种比较有效的变异算子:交换变异(swap mutation)、反转变异(inversion mutation)、移码变异(shift mutation)。
2.3 解码过程
完整的调度方案要通过两个阶段解码过程获得。第一阶段(步骤(1)、(2)将装载、加工、卸载作为一个整体进行解码,并对调度方案进行邻域搜索;第二阶段(步骤(3)~(8)),对整体调度方案中的装卸作业进行人员选择。具体解码过程(步骤)如下:
(1)采用插入式贪婪解码方式,得到完工时间最小的整体方案,再采用改进的N6邻域搜索方法,得到该调度方案的邻域解集Ω。
(2)计算邻域解集Ω中调度方案各工序的最晚开工时间Lijτ。
(3)重置各项作业的开始和完成时间,令Sijτ=Eijτ=-1(τ=1,2,3)。
(4)构建选派作业集合φ,选定装载或卸载作业,并确定该作业的操作人员。
(5)根据式(11)、式(13)计算装卸作业ijτ的开始时间Sijτ,如作业ijτ为装载作业,则根据式(12)计算其后续加工作业的开始时间;之后,再根据式(8)计算作业ijτ的完工时间Eijτ。
(6)判断可解码集合φ是否为空,若为空,则进入步骤(7),若不为空,转入步骤(4)。
(7)依据式(3)~式(6)计算该方案的目标值,并更新外部档案P。
(8)若邻域解集Ω均已进行人员选派,则解码过程结束,否则转入步骤(3)。
2.4 改进的N6邻域搜索方法
采用N6邻域搜索方法对第一阶段解码形成的整体调度方案进行邻域搜索。该邻域搜索方法将关键路径块内的工序移至块首工序前或块尾工序后,创造出更多邻域解,为探索更大的有效解空间提供可能。N6邻域解不能保证最大完工时间最小化,如图3所示,将M2的关键路径中的工序O12移至块首工序O22前,O24后移,使整体调度方案的完成时间延长。因此,本文对N6邻域搜索方法进行完善,使其更加高效地生成多种邻域解。

图3 N6邻域可行性分析
设块首工序为Ouv和块尾工序为Oxy,Obc是Ouv的设备紧前工序,Ode是Oxy的设备紧后工序,现将块内工序Oij移至块首工序Ouv前或块尾工序Oxy后,Aij为工序Oij的加工时间,其中,u、x、b、d为工件编号,u,x,b,d∈{1,2,…,n};v、y、c、e为工序编号,v,y,c,e∈{1,2,…,m}。
首先,为保证块首工序Ouv前和块尾工序Oxy后的设备有空闲时间,使Oij移动后的关键路径块可以整体前移,缩短完成时间,则将Oij移至Ouv前,需满足
Suv>max(Ebc,Eij-1)
(14)
将Oij移至Oxy后,需满足
Exy (15) 其次,为使Oij移动后不产生更长的关键路径,则将Oij移至Ouv前,此时需满足 Aij-(Suv-max(Ebc,Eij-1))< min(Li′j′-Si′j′|i′,j′∈Φ1) (16) 将Oij移至Oxy后,此时需满足 Aij-(min(Sde,Sde+1)-Exy)< min(Si′j′+1-Ei′j′|i′j′∈Φ2) (17) 式中,Φ2为工序Oij与Oxy间的所有工序i′j′组成的集合;i′为工件编号,i′∈{1,2,…,n};j′为工序编号,j′∈{1,2,…,m}。 以式(16)为例,公式左边表示Oij移至Ouv前会使Ouv至Oij前的所有工序i′j′(由集合Φ1表示)后移(延迟)的时间,公式右边表示集合Φ1中工序最晚开始时间与最早开始时间之差的最小值。 2.5.1非支配解集更新 对于新解α,若满足∀k∈{1,2,3,4},Fk(α)≤Fk(β)∧∃k∈{1,2,3,4},Fk(α) 2.5.2基于网格的非支配解排序与选择 利用网格对外部档案中的非支配解集进行划分,并按非支配解在网格中的多样性指标进行排序,再采用锦标赛方法选择非支配解参与种群进化,提高种群的多样性。具体的网格排序与选择过程如下。 首先,计算第k维网格的宽度: (18) 其次,计算非支配解α在第k维目标上的网格坐标: (19) 然后,依据下式计算外部档案中非支配解的多样性排序指标: (20) 图4 基于网格的非支配解排序 最后,按G(α)对非支配解进行降序排序,采用锦标赛法随机确定参与交叉操作的非支配解。 第二阶段解码中,针对装卸作业的人员选择过程和启发式信息设计的步骤如下: (1)将紧前作业已经调度而本作业未调度的装卸作业放入可调度作业集合φ。 (2)选取调度作业集合φ中最晚开始时间Lijτ与最早可开始时间Sijτ差值最小的作业作为下一个选派作业ijτ*。 (3)针对作业ijτ*,采用赌轮法,依据 (21) μa=|max(xa,hgρxa,ijτya,hgρ,ijτEhgρ)-max(xa,ijτSijτ)| (22) 式中,μa为等待操作人员a的时间。 选定操作人员a*。式(21)可以使等待时间短和作业效率高的人员获得更大的选择概率。 为便于应用,本算法仅需设定种群规模N和算法终止条件(进化代数PS)。算法的实现步骤如下: (1)设定算法参数,并令迭代标识ω=0。 (2)种群初始化。依据编码规则,随机生成N个个体作为初始种群,并对其进行解码,计算个体目标函数值,更新外部档案。 (3)种群进化。对于种群中的个体i:首先,从外部档案选取个体j,构成双亲;其次,随机选择交叉算子,交叉生成子代个体i′、j′;再次,任选子代个体,随机选择变异算子,变异生成新个体i″;最后,对子代个体i″进行解码,更新个体i和外部档案。 (4)终止条件判断。ω 以Intel CPU 2.7GHz、RAM 8G为硬件环境,以Windows 10+ Visual Studio Code 1.74.2为软件平台,以作业车间调度测试集LA1~LA40[18]为测试对象,设计了3种对比实验:①基于IBM CPLEX 12.6.3求解器开发了CPLEX_CP(以下简称C-CP)求解模型,并将其与简化的GFEAGA进行对比实验,以验证GFEAGA求解的高效性;②与多目标优化算法NSGA-Ⅱ[19]和MOEA[20]进行对比实验,以验证GFEAGA对多目标问题的求解能力;③通过相似性与学习率的交叉实验,对比分析不同相似性与学习率对调度方案和人员作业的影响,以验证本研究问题的应用效果。 由于本研究问题涉及人员和设备的多种因素,所以需对LA1~LA40测试数据进行相应的完善。其中,设备间行走时间、作业相似性和装卸时间分别取[0.1,0.4]、[0,1]和[1,4]内均匀分布的随机数,并要求任意3个设备间的行走时间满足三角不等式,测试集中,原加工时间扣除装卸时间后作为设备加工时间。与测例集中设备对应,随机生成相应人员的学习因子如表4所示。 表4 人员学习因子对应表 C-CP采用约束满足问题的求解方法,在以最大完工时间为目标的车间调度问题上表现出良好性能,因此通过与其对比来了解GFEAGA的求解性能。 3.1.1参数调整 3.1.2结果分析 设GFEAGA算法种群N为50,将相同求解时间的条件下10次运行的平均结果与C-CP算法的求解结果进行对比。各测例对比详见表5,其中,Cmax为最大完工时间,T为运行时间。 表5 GFEAGA与C-CP实验结果 LA1~LA40测试数据按次序每5个为一组,分别代表了不同的问题规模(n×m)。8组测例(测例1-5、测例6-10、…、测例36-40)的具体规模分别为10×5、15×5、20×5、10×10、15×10、20×10、30×10、15×15。表5中,加粗部分为相对优解。从求解效果分析:①对中小规模问题(LA1~LA14),C-CP与GFEAGA没有明显差异;②较大规模问题(LA15~LA40)上,GFEAGA明显优于C-CP;③从求解均值看,GFEAGA比C-CP的求解效果更好。改进的N6邻域搜索方法使GFEAGA在保持较高求解效率的情况下,获得相对更好的求解效果。 3.2.1参数设置 为验证网格技术对外部档案中非支配解的保留、评价与选择方法的有效性,以多目标求解算法NSGA-Ⅱ和MOEA为对比对象,采用非支配解比例(ratio of nondominated solutions,R-NDS)[21]与超体积(hypervolume,HV)[22]进行算法有效性评价。R-NDS反映算法求得非支配解数量的占优性,R-NDS值越大,算法求得的非支配解越多。HV反映非支配解集空间分布的多样性,HV越大,非支配解集的空间分布越好。将LA1~LA40作为测试数据集,种群规模和进化代数均设置为50,取10次运行的平均结果进行比较。 R-NDS和HV的计算过程如下:①对3种算法的非支配解集进行合并,模拟近似Pareto前沿;②以近似Pareto前沿为参照,计算各算法相应的指标。由表6可见:①从R-NDS看,所有测例中的 GFEAGA较NSGA-Ⅱ和MOEA优势明显,R-NDS的平均胜出率分别为557%和608%,表明GFEAGA能求解数量更多的非支配解;②从HV看,GFEAGA在绝大多数测例中的表现优于NSGA-Ⅱ和MOEA,HV的平均胜出率为9%,表明GFEAGA求得Pareto解集分布的多样性方面更有优势。为更好展示3种算法非支配解集空间分布性,以LA3为例,给出了3种算法在4个目标解集的平行坐标图(图5)。图5中标注了3中算法求得的Pareto解数,展示各目标最小值及解集分布情况。 (a)GFEAGA(250个解) 表6 多目标实验结果指标 3.2.2运行结果分析 GFEAGA能输出更多有效解,在各目标上分布较均匀且均可以达到最优值。根据以上结果分析GFEAGA优于MOEA与NSGA-Ⅱ的原因:①改进的邻域搜索方法提高了领域解集的质量,为生成多样化Pareto解奠定了基础;②人员选派的启发式信息均衡了人员负荷,减少了人员的等待浪费,有助于相关人员优化目标的实现;③外部档案有利于保留更多的非支配个体,保证了非支配解集的多样性;④采用网格技术进行非支配解集的划分及个体选择提高了优良父代的选择率。 3.3.1实验设置 为验证相似性和学习率对本研究问题目标值及人员利用率的影响,以LA1为实验案例,分别将相似性的取值区间[-1,0]和学习率的取值区间[0,1]做10等分后进行交叉实验。每组实验10次,通过目标F1~F3的最小下界分析相似性和学习率对本研究问题求解影响及规律。 3.3.2结果分析 图6反映相似性和学习率变化时,F1~F3的最小下界的变化情况。其中,图6a、图6b反映了相似性和学习率对F1、F2下界有明显且规律的影响,表明在优化总完工时间和人员总负荷时,相似性和学习率应得到重视;图6c反映了相似性和学习率与F3的下界变化具有相关性,表明在优化最大人员负荷时,相似性和学习率也是不可忽视的因素。 (a)F1的下界变化 因此:①“一人多机”模式下,相似性和学习率使制造系统在压缩工期、平衡工作负荷等方面具备更灵活的资源配置能力;②该生产模式下,重视作业相似性并加强人员的选派,是制定精确的生产计划、合理利用人力资源、平衡人员工作负荷的重要基础;③该生产模式下,GFEAGA可以兼顾作业相似性和人员学习差异,为决策者提供更多调度方案选择。 为满足多样化市场需求,在“一人多机”生产模式下,提出了考虑相似学习效应的多目标作业车间调度模型和求解效率高且综合性能好的基于网格筛选外部档案的遗传算法。研究表明:作业相似性和学习效应对人员操作时间均有明显影响,应成为提高生产效率、节约人力资源值得关注的因素;对于该类复杂性更高的调度问题,基于网格筛选外部档案的遗传算法具有很好的局部搜索能力和离散多目标问题搜索能力,可以为企业提供更多灵活实用的调度方案。2.5 基于网格的非支配解选择
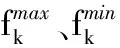




2.6 人员选派
2.7 GFEAGA实现过程
3 实验分析

3.1 与C-CP算法的对比实验及分析


3.2 多目标求解的有效性分析
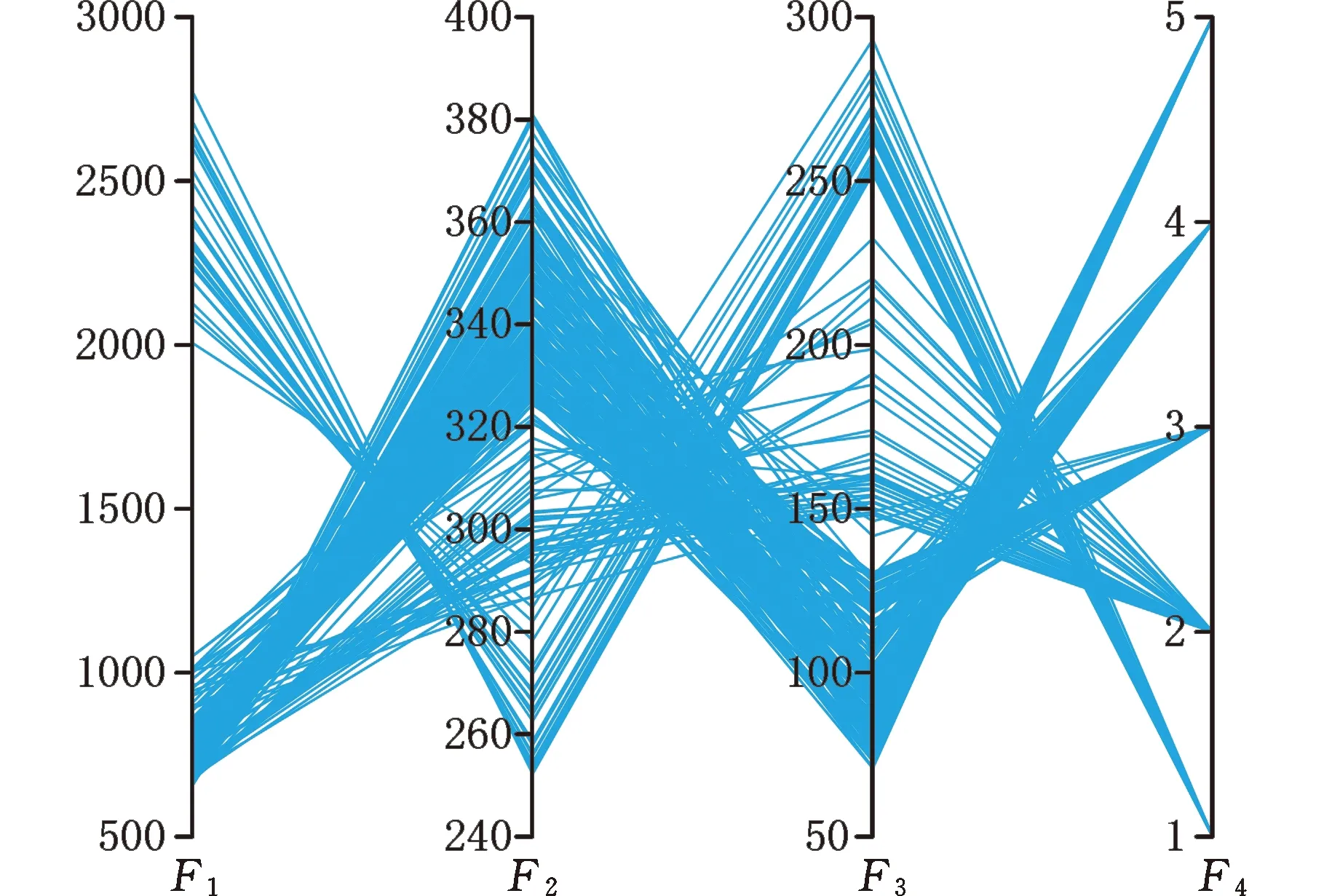
3.3 相似性和学习率对调度效果的影响分析

4 结论

