基于ARIO的灾后区域经济模拟与重建资金分配研究——以湖北省2016年洪灾为例

刘高峰,宁思雨,王慧敏

(1. 河海大学商学院,江苏 南京 211100; 2. 河海大学管理科学研究所,江苏 南京 211100)

受全球气候变化和人类活动的影响,暴雨、洪涝、飓风、高温等极端天气事件发生频次和强度明显增大。重大自然灾害的发生不仅会造成房屋、基础设施、自然资源等有形资产的直接损失,还将通过供给中断和需求减少引起产业密切关联的经济系统发生连锁反应,带来更大的间接损失[1-2]。2016年,我国发生全国大范围洪涝灾害,多地爆发山洪、泥石流、滑坡、塌方、溃堤等险情,其中湖北省受灾最为严重,因洪涝停产工矿企业1977个,工业直接经济损失达17.69亿元,间接经济损失为4.54亿元,严重影响区域经济发展。2021年河南“7·20”特大暴雨灾害,造成全省16市150个县(市、区)1478.6万人受灾,因灾死亡、失踪398人,直接经济损失高达1200.6亿元,灾害导致的交通停运、企业停工停产等间接经济损失更是难以估量。灾后快速恢复重建是确保灾区未来社会经济全面发展、和谐稳定的强有力措施[3]。一般来说,产业经济系统关联性越高,灾害损失就越大[4],灾后经济恢复时间也越长[5]。而重建资金的投入,将影响产业部门获得的超额生产能力,从而缩短经济恢复时间[6-7]。由于不同产业部门经济贡献度不一样,获得不同的灾后重建资金后对经济恢复的推动效果也不一样,因此,灾后重建资金如何在各产业间合理分配,即重建资金“怎么投”可使灾后经济恢复时间最短、恢复效率最高,是亟待解决的难题。

目前对灾后重建资金投入和经济恢复的研究主要以投入产出(input-output,IO)模型和可计算的一般均衡(computable general equilibrium,CGE)模型为主。IO模型是一个静态经济模型,借助产业经济系统的关联结构,将各生产要素的消耗和使用转化为具有一定经济效益的价值产出,已被广泛应用于包括经济、环境、信息等在内的诸多领域,真实反映了各关联主体的经济联系[8],适用于短期的经济动态变化。已有学者利用IO模型的产业关联结构,分析了灾害产生的间接经济损失在产业间的扩散影响及其经济损失变化规律[9-11]。CGE模型是一种动态评估宏观经济政策变化对生产水平影响效果的模拟方法[8],适用于长期经济变化。吴先华等[12]利用CGE模型分析了灾后投入水平对提高经济恢复效率的影响,Hallegatte[13-14]在传统IO模型基础上,考虑生产能力变化并结合区域经济系统特点,提出了区域适应性投入产出(adaptive regional input output,ARIO)模型,可以将灾后生产的动态变化纳入灾后经济模拟中。目前该模型已被应用于评估地震、台风等灾害的灾后社会经济损失及恢复[7,15-16]。还有学者从灾后响应情景出发,模拟不同资源投入对灾后经济恢复时间长短的影响[17-18]。

虽然已有不少学者利用IO模型探究重建资金对灾后经济恢复水平和恢复时间的影响[19-22],解决了灾后经济恢复所需的“投多少”问题,但现有研究一般假设灾后重建资金应按照各部门的生产规模进行均衡投入,忽略了产业部门的经济属性和对灾后经济恢复贡献水平的差异性。本文结合产业经济系统理论及投入产出方法,构建基于ARIO的灾后区域经济模拟模型,设计不同重建资金分配方案,并以湖北省2016年洪灾为例,探讨不同重建资金分配方案对灾后经济恢复的影响。

1 模型构建与方案设定

1.1 基于ARIO的灾后区域经济模拟模型

1.1.1基本原理

为准确计算灾害对区域产业经济系统的影响,利用ARIO模型,在传统投入产出表基础上建立当地投入产出(local input-output,LIO)表,假设生产所需的中间消耗和最终产品可以从受灾区外引入,将灾害冲击造成的直接经济损失以各产业部门生产能力的下降来表示,并根据投入产出基本公式计算初始总产出,直到经济生产达到新的供需平衡状态。各产业部门的生产量可通过下式计算:

(1)

式中:Yi、Yj分别为第i个部门、第j个部门的产出;Ai,j为第i个部门生产过程对第j个部门的产品消耗系数;Dlf,i为对第i个部门的当地最终需求;Ei为第i个部门的出口需求;Dh,i、Dj,i分别为家庭重建、第j个部门重建对第i个部门的需求。当生产量等于总需求时,经济系统达到平衡状态。

1.1.2生产模拟

a.初始生产量。第i个产业部门的初始产量Y0,i可通过下式计算:

Y0,i=(1-A)-1Dtf,i

(2)

式中:A为第i个部门的产品消耗系数;Dtf,i为第i个部门的总最终需求,包括当地最终需求、出口需求和重建需求。

b.生产容量。遭受灾害冲击后,各部门生产能力下降,部门i的灾后生产容量Ycap,i可通过下式计算:

Ycap,i=Y0,i(1-Δi)αi

(3)

式中:Δi为产业部门i的生产资本的损失比例;αi为第i个产业部门的生产能力。如果没有库存的限制,部门i受灾后的生产量Yopt,i等于总需求DT,i和生产容量Ycap,i的最小值,即Yopt,i=min{Ycap,i,DT,i}。

重建资金的投入将为产业经济系统的灾后恢复带来超额的生产能力,假设超额生产能力γ等于重建投入资金(RF)占当年国内生产总值(GDP)的比值,则在重建资金的支持下,最大生产能力αmax=γ+1。当灾区生产能力不足,引入区外新生产量,将使得灾区自身的生产能力出现超额生产的情况,生产能力将持续增加并达到最大。灾后第i个产业部门t+1时段的生产能力αi,t+1可通过下式计算:

(4)

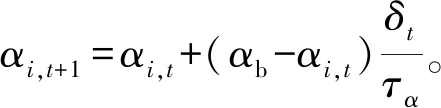
c.库存的影响。在灾后恢复过程中,生产性资产、基础设施等受到灾害冲击,部门生产更依赖于库存。假设现有库存S为产业部门i拥有的部门j的产品库存,Sm为产业部门j的目标库存,Ycap,i(或者总需求DT,i)为一定时间内的最大生产容量。目标库存等于在给定的目标库存补给时间nij内,满足部门i生产所需的部门j的产品量,即Sm=nijmin{Ycap,i,DT,i}Ai,j。假设现有库存低于实际需求库存,生产出现瓶颈,产业部门i的生产就会受到供应其原料的产业部门j的约束,实际需求库存Sr可通过下式计算:

Sr=nijYiAi,j

(5)

目标库存Sm和实际需求库存Sr不一样,前者是保证最大生产所需的量,后者是实际生产所需投入的量,后者将直接影响部门的实际生产。生产部门i的实际最大生产能力Ymax,ij受生产部门j的产品库存限制,计算公式为

(6)

式中ψ为库存不足时生产降低的系数,受经济系统规模和产业部门内企业异质程度影响。受库存影响,产业部门i的实际生产量等于受所有部门限制影响下的产能最小值。

1.1.3需求模拟

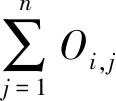
(7)

式中:τist为部门i目标库存恢复的适应性时间参数,假设所有部门相同。最终需求Dtf,i包含当地最终需求Dlf,i、出口需求Ei和重建需求Ri。

重建需求表示灾后修复和重置家庭部门和产业部门破坏产生的需求,每一阶段获取的总重建量ΔRi、家庭重建量ΔDh,i和产业部门重建量ΔDj,i可通过下式计算:

(8)

式中:Oi、O0,i分别为产业部门i的实际需求和初始需求。灾后生产增加有效减少了灾害破坏造成的经济影响,因此重建需求会不断减少。综上,可以得到:

(9)

重复上述迭代过程,当总需求DT,i与实际生产量Yi相等时,产业部门i能恢复到灾前的供给状态,迭代结束。

1.2 重建资金在不同产业间的分配方案设定

为探究重建资金在不同产业部门的分配方案对灾后经济恢复的影响,本文根据产业部门的经济属性和实际灾损情况,将重建资金投入分配方案分为3种:均衡投入、高贡献产业优先、灾损弥补与高贡献产业优先相结合。根据上述灾后区域经济模拟框架,计算不同重建资金分配方案下的灾后经济恢复变化。

1.2.1均衡投入方案

将灾后重建资金按照各产业部门的生产规模(各产业部门GDP占国民经济总值的比)进行分配。假设均衡投入方案灾后重建资金总额为Ftr,则产业部门i按生产规模大小获得灾后重建资金Fire:

(10)

式中:Gi为产业部门i的GDP;n为产业部门数。均衡投入方案各产业部门新的生产能力即为Fire/Gi。不断迭代生产和需求过程,当生产水平满足灾后需求时,得到该方案下的灾后经济恢复时间te。

1.2.2高贡献产业优先方案

产业部门对国民经济的贡献一般是通过资源投入、经济关联等方式带动产业部门生产、消费水平的变化,从而引起总产值的变化[23-24]。基于区域适应性投入产出方法,计算不同产业对区域经济的贡献率,按照贡献率对重建资金进行分配。各产业部门对国民经济发展的贡献Et等于直接经济贡献Ez和间接经济贡献Ej(包含前向产业推动贡献Eq、后向产业拉动贡献Eh和消费波及贡献Ex)之和。各产业部门对国民经济发展的贡献Et可通过下式计算:

Et=Ez+Ej=Ez+Eq+Eh+Ex

(11)

其中Ez=ZTΔXEq=WZΔXEh=ZTBΔX

Z=(zj)zj=gj/Qj

式中:Z为各产业部门的增加值系数向量;gj为产业部门j的GDP增加值;Qj为产业部门j的总产出;ΔX为各产业部门的投入增加值向量;W为完全分配系数;B为完全消耗系数;c为消费乘数。

高贡献产业优先方案各产业部门获得的灾后重建资金Firf可用下式表示:

(12)

此时,各部门新的生产能力即为Firf/Gi。不断迭代生产和需求过程,当生产水平满足灾后需求时,得到该方案下灾后经济恢复时间tf。

1.2.3灾损弥补与高贡献产业优先相结合方案

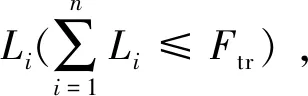
(13)

该方案各部门新的生产能力即为Firc/Gi,不断迭代生产和需求过程,当生产水平满足灾后需求时,得到该方案下灾后经济恢复时间tc。

2 数据来源与模型参数设定

2.1 数据来源

考虑灾害对社会经济间接影响和灾后恢复重建的典型性及相关数据的可得性,本文选取湖北省2016年6—7月间的暴雨洪涝灾害为实证研究对象。湖北省是长江经济带最重要省份之一,地处亚热带,受每年梅雨季节和东亚季风气候的影响,地区强降雨多且频繁,易发生洪涝灾害,严重制约了当地经济的发展。2016年6月18日至7月21日梅雨期间,湖北省连续遭受6场大范围强降雨,全省受灾严重,共造成直接经济损失750.60亿元。由于投入产出表一般以省为单位编制,且湖北省全省均遭受严重洪灾,因此本文将利用投入产出表描述湖北省国民经济各部门间的投入和产出,运用ARIO模型模拟该省灾后经济恢复过程。

社会经济数据来源于《湖北省统计年鉴2017》《2012年湖北省投入产出表》《2016年湖北省国民经济和社会发展统计公报》,洪涝灾害数据来源于《2016中国水旱灾害公报》、水利部2016年统计数据以及2016年湖北省政府发布的《湖北省灾后恢复重建总体方案》。本文基于湖北省2012年的传统投入产出表,将原42部门合并为国民经济核算中的15大产业类型[9],其固定资产及直接损失见表1。国家和湖北省共投资698亿元用于灾后恢复重建,占湖北省当年GDP的2.14%[25],根据式(4),其最大生产能力为102.14%。

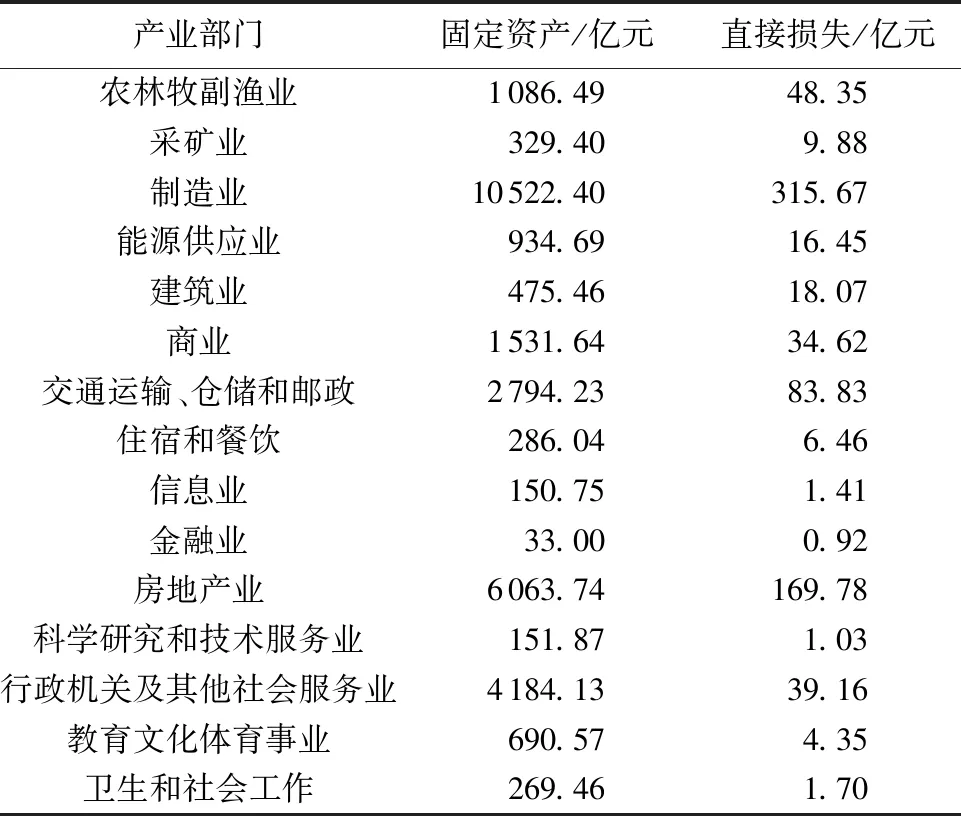
表1 湖北省2016年15个部门固定资产及直接损失

2.2 模型参数设定

根据已有研究[6,13-14,18]和湖北省实际情况,对适应性时间参数、目标库存补给时间、时间模拟步长等参数进行设定。①生产能力的适应性时间参数τα表示获得的重建资金投入在一段时间τα内使生产能力达到最大,假定τα=360d,所有部门都相同;库存恢复的适应性时间参数τist表示库存将在一段时间τist内恢复,假定τist=30d,所有部门也相同。②目标库存补给时间nij为部门i对部门j商品的库存补给所需要的时间,假设nij=60d。③假定模拟时间步长δt=1d。

3 结果与分析

3.1 产业部门生产增加值随时间变化的关系

根据2012年当地投入产出和2016年洪涝灾害后各产业的直接损失数据,模拟了湖北省灾后区域经济的生产与需求变化,计算在实际投入698亿元情况下(此时αmax=102.14%)灾后区域经济恢复变化情况。图1为湖北省洪灾后经济恢复期间生产增加值的变化率,生产增加值变化率呈现先骤减后快速恢复并缓慢趋于平稳的特点。

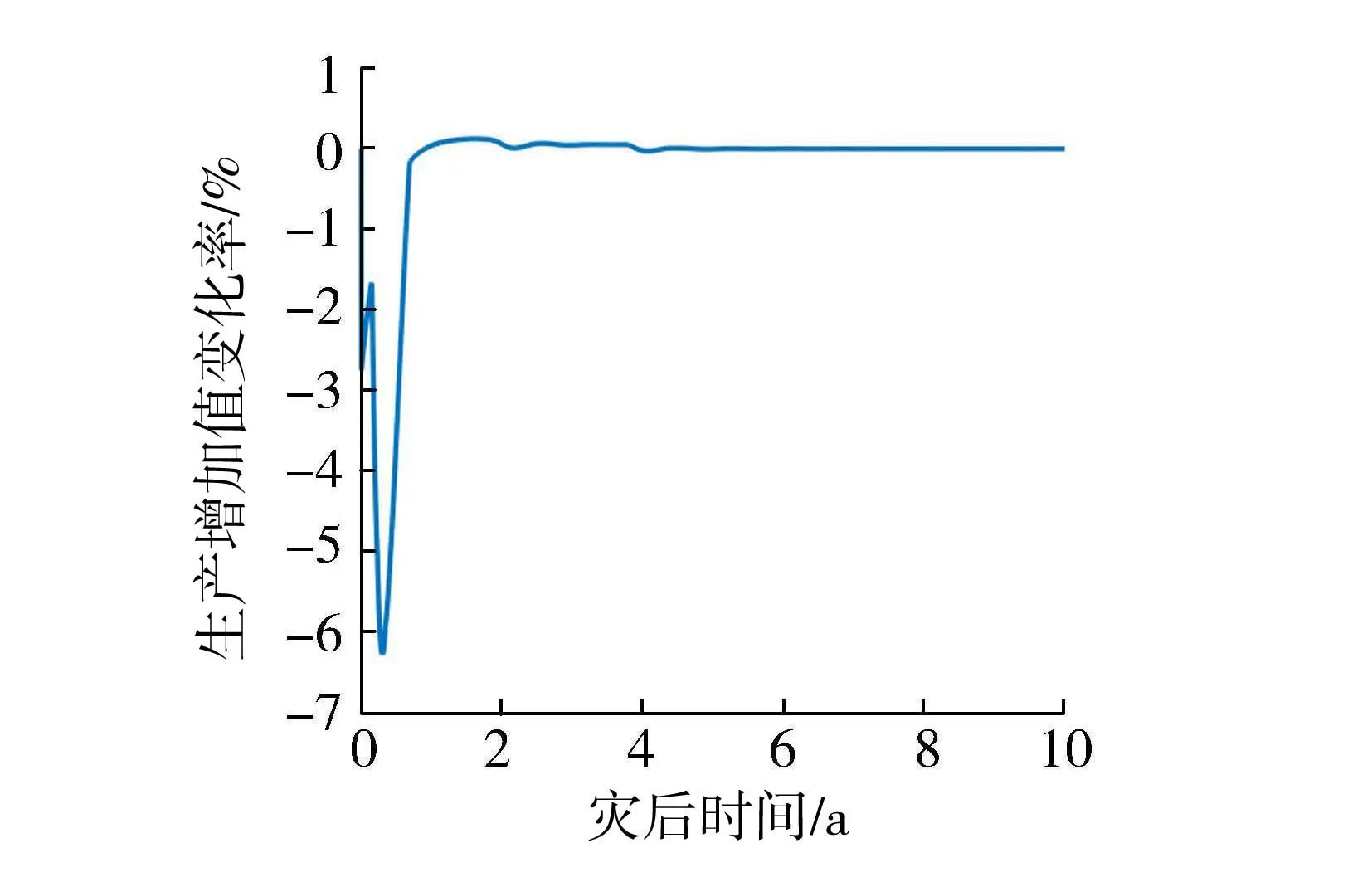
图1 湖北省洪灾后经济恢复期间生产增加值变化率

一般认为,灾后经济恢复是指从开始受到灾害冲击到区域经济重新恢复到灾前水平,并满足正常生产生活需要所经历的阶段。但是,从灾后重建的角度出发,区域经济能满足重建需求和生产所需就预示着灾后重建结束。因此,灾后重建恢复视角下的区域经济恢复时间,是指受到灾害冲击开始到灾后重建结束所经历的时间。产业部门生产增加值在灾后经历了4个阶段(表2)。在T1阶段,灾害直接破坏厂房设备等生产性资产,在短时间内导致生产骤减。而后,由于产业间的关联性,区域经济系统内其他产业的生产水平持续下降,下降幅度最大为6.28%。在T2阶段,由于灾后重建资金的投入,灾后生产在一定时间内获得了极大的超额生产能力,生产水平不断提升,在重建工作进行11月左右,恢复至灾前水平。但是,由于灾后重建带来了更高的需求,拉动生产持续增加,直至第19个月后生产增加值达到最高。在T3和T4阶段,由于重建需求的减少会产生产量过剩,最终生产和需求减少并逐步趋于稳定,直至洪涝灾后第98月,经济回到灾前水平。本文所指的区域经济恢复时间是0～T3时间段,即从灾害发生到重建结束所经历的时间。2016年湖北省政府实际投入698亿元的重建资金,模拟得到湖北省洪灾后经济恢复期约为598d。根据湖北省政府公布的《2017年湖北政府工作报告》《2018年湖北政府工作报告》,截至2018年2月,湖北省2016年暴雨洪灾后经济恢复重建工作基本完成,共历时20月,与本文模拟值598d非常接近。因此,本文建立的灾后经济恢复时间模拟模型能反映湖北省2016年洪灾后区域经济的变化。

表2 灾后经济恢复中生产增加值变化阶段

3.2 不同重建投入资金与灾后经济恢复时间关系

灾后一定时间内能达到的αmax在100%、102.14%、110%、120%、150%情景下灾后经济恢复的变化与恢复时间见表3(后3种情况均超出正常生产能力)。随着αmax的提升,生产增加值的下降幅度不断减小,从下降6.44%减小到下降3.69%。由于生产能力的提升幅度变大,且产业间关联扩散导致的间接损失也不断下降,在无超额生产能力的情况下,间接损失达588.61亿元,超额生产能力提升10%,间接损失下降30%左右。生产增加值变化率最大值也随着αmax的提高而变大。在无超额生产能力的情况下,生产缓慢恢复,在灾后3203d回到灾前水平,生产增加值与灾前相比无增加;最大生产能力为110%时,生产增加值上升0.52%,重建结束时间为445d;但当最大生产能力提升到150%时,生产增加值上升1.98%,与最大生产能力110%时相比,重建恢复时间仅缩短了137d。

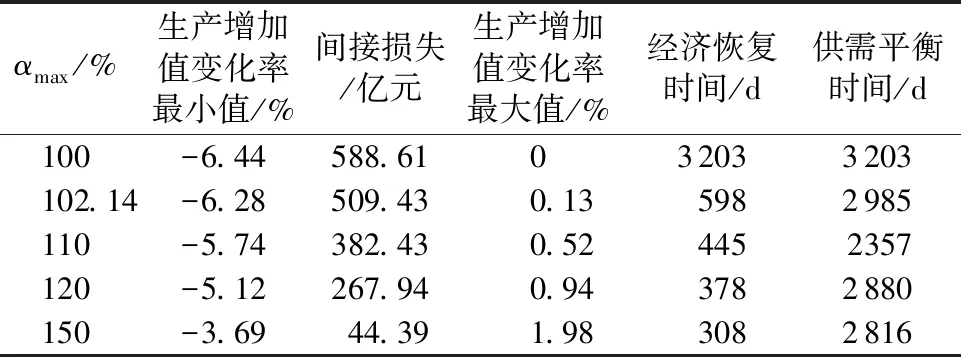
表3 不同最大生产能力下生产增加值变化、间接损失与经济恢复时间

分析表3发现,最大生产能力越高,间接损失越小,重建恢复时间越短。同时也发现,最大生产能力越高,其最大生产增加值越高,由于区域经济需要一定适应过程,在其恢复平衡过程中,表现出较明显的震荡性,如当最大生产能力提升到150%时,在恢复初期出现较明显的震荡,随后逐步趋于平稳。由于最大超额能力是由重建投入资金的大小决定的,洪灾后经济恢复时间随着灾后重建投入资金的增加而不断缩短,重建资金与灾后恢复时间呈指数关系(图2)。当重建投入资金为6453亿元,即占2016年湖北省GDP的20%时,灾后经济恢复时间为378d,比实际投入698亿元的经济恢复时间缩短半年多,如果重建资金继续增加至GDP的50%时,灾后经济恢复时间为308d,仅缩短了70d。

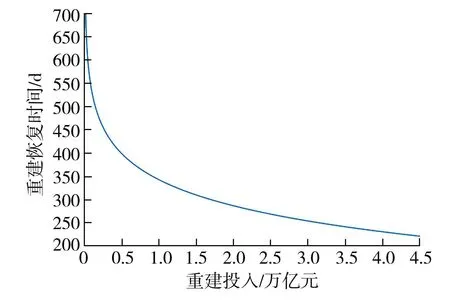
图2 重建资金变化对灾后经济恢复时间的影响

3.3 不同重建资金分配方案下灾后经济恢复时间

为分析重建资金分配对重建时间的影响,设定重建投入资金达到2016年湖北省GDP的20%,即重建投入资金为6453亿元(此时αmax=120%),模拟均衡投入(方案1)、高贡献产业优先(方案2)、 灾损弥补与高贡献产业优先相结合(方案3)3种重建资金分配方案下的灾后经济恢复时间(表4)。由于仅能获取农业、工业、建筑业、批发和零售、交通运输和仓储、住宿和餐饮、金融业、房地产业、其他等9部门的数据,因此将采矿业、制造业、能源供应业合并为工业,假设这3个产业能达到的最大生产能力相同;将信息业、科学研究和技术服务业、行政机关及其他社会服务业、教育文化体育事业、卫生和社会工作合并为其他产业,假设这5个产业能达到的最大生产能力也相同。

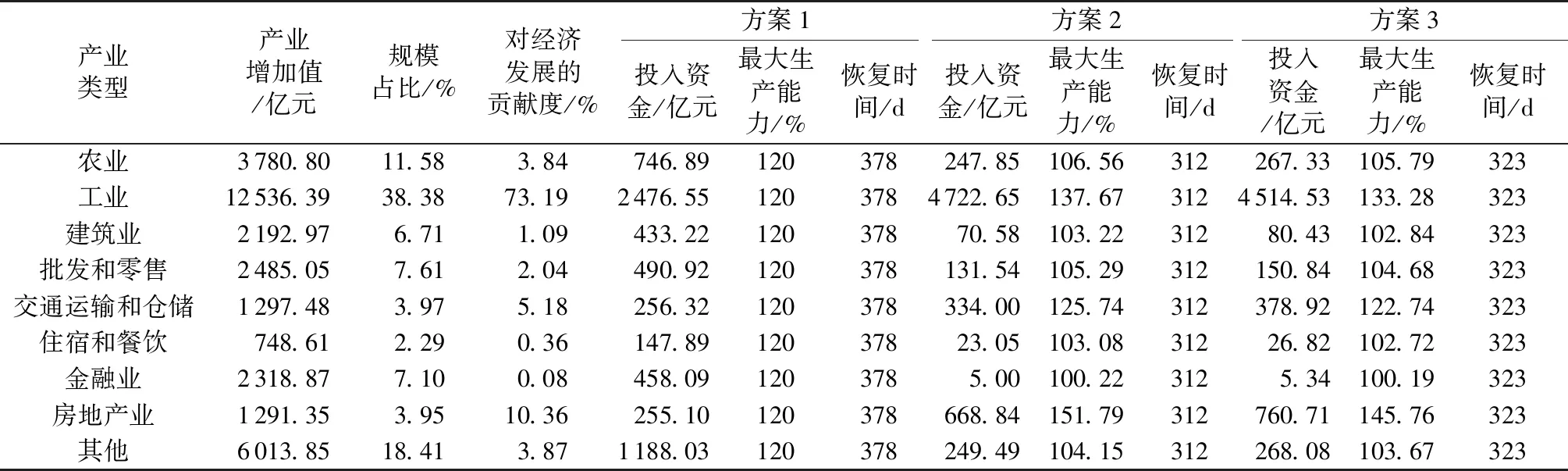
表4 3种情景下的资金分配方案、最大生产能力及经济恢复时间

3种重建资金分配方案下灾后经济恢复时间差异显著。按恢复期从短到长的方案顺序是:方案2(312d)、方案3(323d)、方案1(378d)。在方案1下,重建资金根据各产业增加值占GDP比例进行分配,得到各产业的最大生产能力相同,均为120%;在方案2下,重建资金根据各产业对国民经济发展贡献率的比例进行分配,工业、房地产业、交通运输和仓储产业获取重建资金较多。由于这3个产业的大力拉动,区域经济恢复时间为312d,比方案1缩短66d。因此,将重建资金分配在对国民经济贡献较大的产业能有效缩短经济恢复时间;方案3将一部分资金用于弥补损失、保障民生,各产业能获取的重建资金较方案2少,各产业能达到的最大生产能力也较低。因此,方案3下经济恢复时间较方案2长11d。

4 结 语

区域经济从受到灾害冲击到恢复灾前平衡状态历经4个阶段:生产骤减损失不断扩大、生产快速回到灾前生产水平、生产持续增加、生产回到灾前平衡状态。从湖北省2016年洪灾后经济恢复过程发现,灾后111d内生产增加值一直下降,表明损失不断加大,这也是灾害防控的关键时期。生产增加值快速下降是由于产业关联带来的间接损失直接影响区域经济的恢复。因此,要完善自然灾害损失统计制度,重视灾害扩散引起的间接经济损失,建立科学、全面的灾害损失评估体系,开展自然灾害间接经济损失及宏观经济影响、灾害对贫困与区域发展影响等方面的研究,为灾区灾后恢复重建提供决策支撑。

洪灾后经济恢复时间与重建资金呈指数关系。随着重建资金投入的增加,区域灾后经济恢复时间不断减少。当湖北省重建资金投入为GDP的20%时,灾后经济恢复时间为378d,比实际投入698亿元时经济恢复时间缩短半年多。可见,加大重建资金投入力度、健全灾后重建资金筹措机制非常重要。积极争取中央支持,加大地方各级投入力度,建立健全政府主导、社会多元化投入的资金筹措机制,建立多渠道的社会资金动员和参与机制,积极运用市场机制动员企业参与灾后重建,有助于减少灾后重建时间,增强区域经济恢复能力。

在“以保障安全和改善民生为核心”的国家灾后重建理念指导下,灾损弥补与高贡献产业优先相结合方案比高贡献产业优先方案更优。从湖北省2016年洪灾后重建实证分析过程发现,高贡献产业优先方案下灾后经济恢复时间比均衡投入方案缩短66d,但比灾损弥补与高贡献产业优先相结合方案仅缩短11d。因此,可以优先考虑灾损弥补与高贡献产业优先相结合方案,先将一部分重建资金用于弥补灾害损失来保障民生和基本生产生活,然后将剩下的资金分配在对国民经济贡献较大的产业,从而进一步建立健全洪涝灾害后重建资金分配使用制度,提高灾后重建效率。