陀螺全站仪在合肥轨道交通定向测量中的应用分析

付先国 （合肥市测绘设计研究院有限公司，安徽 合肥 230061）

1 引言

目前国内很多大中型城市都在开展城市轨道交通建设，城市轨道交通工程施工一般采用单向掘进，在单向掘进中如何保证轨道工程顺利贯通是一大重点。而方位控制是保证轨道交通工程顺利贯通的前提条件。由于受到轨道交通工程场地条件的限制，地下平面控制网只能布设成狭长带状网形，且一般只能采用导线法进行布设。但是在测量过程中，随着测站数的增加，测量精度会逐步降低。为确保轨道工程顺利贯通，《城市轨道交通工程测量规范》（GB/T 50308-2017）规定，“当隧道单向贯通距离大于1500 m 时，应采用高精度联系测量或增加联系测量次数等方法，提高定向测量精度。”

2 GYROMAT-3000型陀螺全站仪简介

GYROMAT-3000 全自动精密陀螺全站仪是德国DMT 公司的产品，标称精度为3″，实际认定一次定向中误差为5″，是当今精度最高、稳定性最好的通用陀螺全站仪。在仪器内部，悬挂一个绝缘、高速旋转的陀螺，轴在陀螺自身运动、地球引力及地球旋转的联合作用下绕北方向摆动。因此，仪器内特制的光电扫描系统能全自动并及高精度确认出北方向。此外，仪器运行速度快，完成一次定向测量只需10min，测量精度为1/1000gon，相当于每千米仅有15mm 误差。

图1 GYROMAT-3000型陀螺全站仪

3 陀螺全站仪的定向原理

3.1 定向原理

陀螺全站仪定向主要利用陀螺全站仪自动寻北的原理。陀螺全站仪的工作原理是用吊丝悬挂重心下移的陀螺灵敏部敏感地球自转角速度的水平分量，在重力的作用下，产生一个北向进动的力矩，使陀螺敏感部主轴围绕子午面往复摆动，通过光电传感器将陀螺敏感部往复摆动的光信号，转换为电信号，传送给控制系统，控制系统自动跟踪陀螺灵敏部的方位摆动，并对灵敏部进行加矩控制，算出被测目标的真北向方位角。

3.2 陀螺定向中坐标方位角计算

地面任意一点有三个基准方向，即坐标北、真北、磁北方向，通常称为“三北方向”。三北方向之间的夹角称为偏角，偏角有子午线收敛角、磁偏角。在高斯平面直角坐标系中，纵坐标轴所指的方向称为坐标北方向，以坐标纵轴方向为基准方向的方位角称为坐标方位角；地球上某点的真子午线的切线方向为该点的真北方向，以真北方向为基准方向的方位角称为真方位角；真方位角与坐标方位角之间的差值称为子午线收敛角。若坐标北方向在真北方向东侧时，子午线收敛角为正；若坐标北方向在真北方向西侧时，子午线收敛角为负。陀螺全站仪轴的稳定位置通常情况下不与地理子午线重合，二者之间的夹角称为陀螺仪的仪器常数。若陀螺全站仪稳定位置位于地理子午线的东侧，则陀螺全站仪的仪器常数为正；若陀螺全站仪稳定位置位于地理子午线的西侧，则陀螺全站仪的仪器常数为负。相关研究表明，陀螺全站仪的仪器常数是一个随地点和时间的变化而变化的量，因此一般规定陀螺定向的整个过程应在三昼夜内完成，避免时间过长造成仪器常数发生变化。

在高斯平面直角坐标系中，真方位角与坐标方位角关系公式为：

真方位角与陀螺方位角关系公式为：

以上两式中：A为测线的真方位角；α为测线的坐标方位角；γ为测站点的子午线收敛角，T为陀螺定向测量值；Δ 为仪器常数值。

由式（1）、式（2）可以得出：

将上式（3）带入式（4）可以得出：

可得：

δγ表示地上已知点测站和地下隧道内未知点测站的子午线收敛角的差值，δγ可按式（7）求得。

式中：δγ的单位为秒；μ= 32.23tanϕ（此公式在地面和隧道定向点的距离不超过10 km，纬度小于60°时采用），ϕ为当地纬度；y已知边和y隧道内为地上定向边已知测站点和地下定向边测站点的横坐标（以km为单位）。

利用坐标值反算的坐标方位角由式（8）计算获得。

4 工程实例

本文以合肥市轨道交通1 号线三期工程物流大道站-瑶海公园站地下区间的陀螺定向为例进行分析。合肥市轨道交通1 号线三期工程线路全长4.530 km，共设三个车站和一个停车场，分别为天水路站、物流大道站、瑶海公园站和天水路停车场。物流大道站-瑶海公园站区间左线起点里程为左K14+366.680，终点里程为左K15+898.879，短链18.428 m，区间长度为1513.771 m；右线起点里程为右K14+366.680，终点里程为右K15+898.879，区间长度为1532.199 m。左右线间距为11.800～15.000 m，平面曲线最小曲线半径为350.000 m。本区间线路的最低点位于里程左K15+324.113 附近，在此位置设置一座区间联络通道及泵站，并在里程左K14+830.613 设置一座区间联络通道，均采用矿山法施工。

为了提高轨道工程区间内导线的定向精度，确保轨道工程顺利贯通，采用GYROMAT3000 型陀螺全站仪。在盾构机掘进至约750 m 节点时，在物流大道站-瑶海公园站区间左右线分别选择了两条导线边进行陀螺定向，并与全站仪导线法所测得坐标方位角进行比较，确定是否需要进行陀螺定向改正。

4.1 陀螺全站仪的定向测量

根据《城市轨道交通工程测量规范》（GB/T 50308-2017），地下定向边陀螺方位角测量采用“3（地上）—3（地下）—3（回到地上）”的测量流程，即在地面已知边上先观测3 个测回，然后在隧道内待测边上观测3 个测回（左线和右线分别观测），最后再回到已知边观测3 个测回。

陀螺全站仪定向的作业过程如下所示。

①地上已知边测量。在盾构机掘进至约750m 节点时，选择地上已知边GPS4-GPS5 进行陀螺全站仪定向测量，设站点为GPS4，目标方向点为GPS5。观测3 个测回，3 个测回的测回间较差应小于20″。

②地下待定边测量。选择左线WYZ510→WYZ685、右线WYY516→WYY704 为地下定向边，设站点分别为WYZ510 和WYY516，目标方向点分别为WYZ685 和WYY704。左、右线定向测量分别观测3个测回，3个测回的测回间较差应小于20″。

③测后地上已知边测量。在完成轨道区间左右线的定向测量后，再次回到地面进行地面已知边定向测量。回到地面再次测定仪器常数的目的，一是检验陀螺全站仪的仪器常数是否存在漂移，二是提高仪器常数值的精度。当测前、测后两次测定的仪器常数的较差值不超过规范规定的要求时，取其平均值作为最终的仪器常数值。按照与①同样的作业过程，设站点为GPS4，目标方向点为GPS5。观测3 个测回，3 个测回的测回间较差同样应小于20″。

4.2 数据分析与处理

陀螺全站仪所测地上、地下控制边的数据见表2-表4所示。

通过表2-表4 可知，边GPS4→GPS5 测前陀螺方位角测回间最大互差为4.7″、测后陀螺方位角测回间最大互差为5.5″ ，左线定向边WYZ510→WYZ685 陀螺方位角测回间最大互差为7.3″，右线定向边WYY516→WYY704陀螺方位角测回间最大互差为2.0″，满足规范中“测回间陀螺方位角较差应小于20″”的要求；边GPS4→GPS5 测前、测后陀螺方位角平均值较差为0.7″，满足规范中“测前、测后陀螺仪仪器常数平均值的较差应小于15″”的要求。

根据表1 中地面已知边控制点坐标，利用式（8）计算得到GPS4→GPS5的坐标方位角αGPS4→GPS5=106°10'18.2″。

表1 已知点及定向点坐标成果表

表2 测前地上已知边实测数据表

表3 测后地上已知边实测数据表

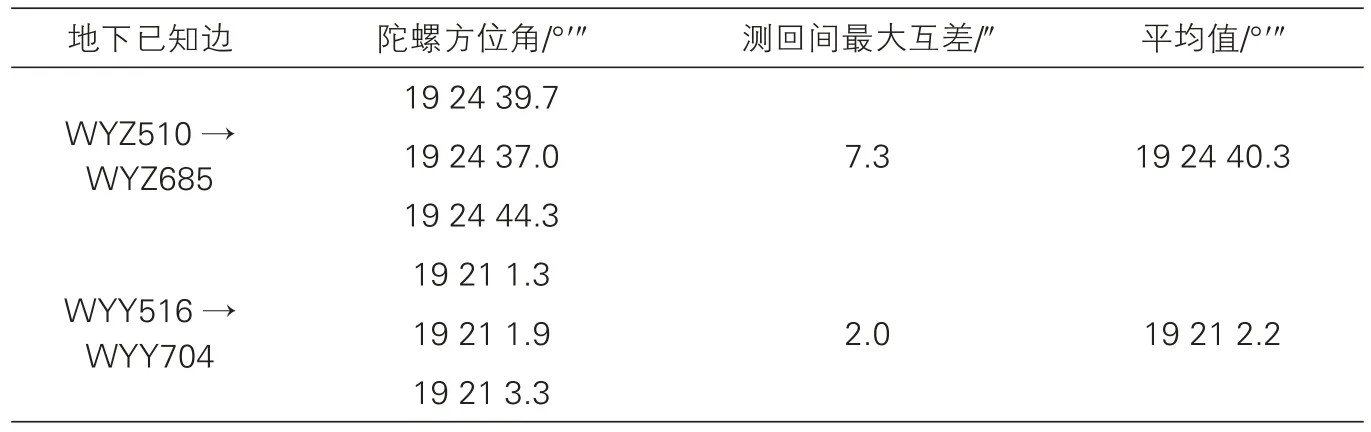
表4 地下定向边实测数据表

根据式（6）、式（7）和表1 中已知点、定向点的坐标，可计算地上已知边测站点与轨道区间内定向边测站点之间子午线收敛角的差值，如表5所示。

表5 子午线收敛角差值表

根据式（5）和上面的计算结果，可得陀螺定向中定向边的坐标方位角。计算结果见表6。

表6 陀螺定向坐标方位角成果表

根据表1 中的坐标值和式（8）可计算得到导线测量法的坐标方位角，陀螺定向的坐标方位角与导线法的坐标方位角比较如表7所示。

表7 坐标方位角差值比较表

根据表7 可知，本次陀螺全站仪测量得到的坐标方位角与导线法坐标反算的坐标方位角的较差分别为-3.4″、4.4″，较差值均满足规范要求，说明该区间导线精度高，成果可指导该区间正常施工。

4.3 精度评定

陀螺全站仪的定向精度是以观测值的中误差作为评定指标。观测值的中误差指在相同的观测条件下，对某一目标进行多次观测，通过得到的观测值的改正值计算观测值的中误差。其计算公式如式（9）所示：

式中：n 为总观测次数；V 为该次定向观测值与该组定向测量平均值的差。

根据式（9），结合本次定向测量共4组观测目标、12 个观测数据，可计算得到该台陀螺全站仪的观测中误差为±2.4″。

5 结束语

本文介绍了陀螺全站仪的定向原理和陀螺定向中坐标方位角的计算方法，并以合肥市轨道交通1 号线三期工程物流大道站-瑶海公园站中定向测量为例，阐述了定向测量具体的实施过程，并对定向测量结果进行了分析和精度评定。根据定向测量结果表明，用陀螺全站仪进行定向测量可以有效地检核轨道工程区间内导线法获取的坐标方位角的可靠性，提高轨道定向精度。