修圆角形过渡阶梯对阶梯溢流坝消能特性的影响

陈卫星 熊长鑫 杨具瑞

(1.庐江县水务局,安徽 合肥 231500;2.昆明理工大学现代农业工程学院,云南 昆明 650500;3.长江勘测规划设计研究有限责任公司,湖北 武汉 430019)

自20世纪以来,在中、小单宽流量的泄水建筑物中,阶梯溢流坝在消能方面表现出非常重要的作用。而大单宽流量的泄水建筑物采用阶梯溢流坝消能会受到限制,阶梯溢流坝面可能会出现空蚀、空化破坏,严重危害水工建筑物的稳定运行,比如在1973年,丹江口水库泄洪的单宽流量达到120m3/(s·m)时,阶梯面上出现了大面积的空蚀现象[1]。基于以上问题,我国提出了“宽尾墩+阶梯溢流坝+消力池”一体化消能工的消能方式,此种消能方式分三步消能:第一步消能主要依靠在阶梯溢流坝上游设置的宽尾墩,目的是将水体破碎,通过增大与空气接触、碰撞的面积消能;第二步消能是通过阶梯溢流坝消能,水流滑过阶梯溢流坝,在阶梯内形成横向的旋滚水流,产生的剪切水流与上方主流存在动量和能量的交换[2],在交换的过程中消耗能量;第三步消能是依靠水流在消力池的水跃及壅水作用消能。这种“宽尾墩+阶梯溢流坝+消力池”的一体化消能方式极大地提高了高坝的消能效率。但是,近些年一些高坝在运行过程中出现空蚀空化破坏,如阿海水电站在运行不到半年的时间内,阶梯面出现了大大小小的空蚀坑[3],水东水电站也遇到了同样的破坏[4],说明当今高坝一体化消能面临的主要问题是阶梯空蚀破坏。因此,在高效率消能的前提下,阶梯面发生空蚀空化破坏这一问题亟须解决。

为了解决以上问题,前人在避免阶梯发生空蚀空化破坏方面做了大量研究。如:后小霞等通过数值模拟,发现当宽尾墩的收缩比较小时,其空腔长度较长,掺气较为充分,虽然负压分布较广,但是最大负压值较小,对阶梯空蚀破坏的影响较小[5];刘善均等发现,在宽尾墩与阶梯溢流坝的衔接处增设掺气坎,可以消除前几级阶梯存在的底部清水区,整个阶梯底面和竖直面均有足够的掺气效果[6];此外,适当地改变掺气坎的高度[7]与宽度[8],可以有效地改善掺气空腔的长度,掺气更加充分,可有效地保护阶梯免受空蚀空化破坏;张勤等通过水工模型试验发现,不仅仅掺气坎能改变水流的流态,增大掺气空腔,适当地改变阶梯溢流坝段的首级阶梯台面角,亦可以增大阶梯面的无水区范围,提高掺气能力[9];陈卫星等通过水工模型试验对过渡阶梯段的组合型式阶梯进行正交分析,发现改变组合型式阶梯的阶梯数量与阶梯尺寸,坝面的掺气空腔、掺气浓度及负压也均会发生变化,且阶梯数量对坝面掺气的影响程度较大[10]。上述研究表明,掺气坎、溢流坝面阶梯的形状,尤其是过渡阶梯段的阶梯形状,有助于改善阶梯溢流坝消能的效果。因此,本文以阿海水电站的一体化消能工为原型,在传统型式阶梯溢流坝的基础上,将前六级阶梯设计为不同圆角半径的修圆角形阶梯,按照1000年一遇的标准,以1∶60的模型比尺对原型进行缩放,通过k-ε模型联合VOF的数值模拟方法,对阶梯溢流坝面的压力及紊动动能等水力特性变化进行研究,探究不同圆角半径的修圆角形过渡阶梯的消能影响,对完善高坝阶梯消能形式具有重要的意义。

1 数学模型

1.1 控制方程

本文采用RNGk-ε双方程紊流数学模型[11],对流场进行数值模拟,方程如下:

连续方程:

(1)

动量方程:

(2)

k方程:

(3)

ε方程:

(4)

式中:ρ为混合流体的密度,kg/m3;t为时间,s;xi、xj分别为坐标分量,i、j分别为1,2,3;ui为xi方向的瞬时速度分量,m/s;μ为分子黏性系数,Pa·s;μt为紊流黏滞系数,Pa·s;p为修正压力,Pa;k为紊动动能,J;ε为紊动耗散率;G为平均梯度产生的湍动能生成项;σk、σε分别为k和ε的紊流普朗特数,σk=1.0,σε=1.3;C1ε、C2ε为ε方程的常数,分别为1.44、1.92。

1.2 模拟自由表面的VOF方法

VOF方法,指通过单元网格内水流占单元网格体积的比例F(x,y,z,t)确定自由面,进而追踪水流运动状态的一种方法。当F(x,y,z,t)=0时,表明该单元区域内无水;当F(x,y,z,t)=1时,表明该单元区域内充满水体;当F(x,y,z,t)介于0到1之间时,表明该单元区域内水气混合。因此可以说明每个单元中,水和气的总体积分数为1。这与单相流相比,多出一个体积分数变量。水的体积分数与气的体积分数之间的关系如下:

αw=1-αa

(5)

式中:αw为水的体积分数;αa为气的体积分数。

VOF方法中的密度ρ和黏性系数μ可由下式得出:

ρ=αwρw+(1-αw)ρa

(6)

μ=αwμw+(1-αw)μa

(7)

式中:αw为水的体积分数;ρw、ρa分别为水和气的密度,kg/m3;μw、μa分别为水和气的分子黏性系数,Pa·s。

2 几何模型及数值模拟验证

2.1 几何模型

将阿海水电站一体化消能工按照1∶60的比尺缩放,对其模型进行数值模拟试验。数值模拟的阶梯溢流坝高度为29m,宽度为18m。阶梯溢流坝前与WES曲面相连接,在阶梯溢流坝与WES曲面的衔接处增设一个角度10°、高度1m的掺气坎。在坡度为1V∶0.75H的溢流坝面设置29级阶梯,依次编号为1号,2号,……,29号,其中前6级阶梯为过渡阶梯,后23级阶梯为均匀阶梯,均匀阶梯的尺寸为1m×0.75m(高×宽)。

本数值模拟试验在上述阶梯溢流坝的基础上,将过渡阶梯段的阶梯外直角设计为圆角半径分别为0.188m、0.219m、0.250m的修圆角,形成修圆角形阶梯,圆角半径范围为阶梯水平面的1/4～1/3之间。探究不同半径修圆角形的过渡阶梯对阶梯溢流坝面消能特性的影响。

2.2 网格划分

本次数值模拟试验利用UG、Fluent等商业软件完成。由于本文研究的流场较为复杂,整个流场采用结构化网格离散,同时灵活地处理复杂的计算区域,从而提高准确度。由于对不同的计算区域要求精度不同,所以采用分区域划分方法对整个模型进行网格划分,根据网格疏密适当的原则,对宽尾墩、阶梯溢流坝面等形状复杂区域进行网格加密,结构规则的区域采用正方体结构网格进行填充。方程采用有限体积法离散,方程的对流扩散项采用一阶迎风格式离散,其精度较高。VOF模型的压力与速度采用PISO算法耦合,其可以通过邻值修正和扭曲率修正加快收敛的迭代次数,从而提高计算效率。具体网格划分见图1。

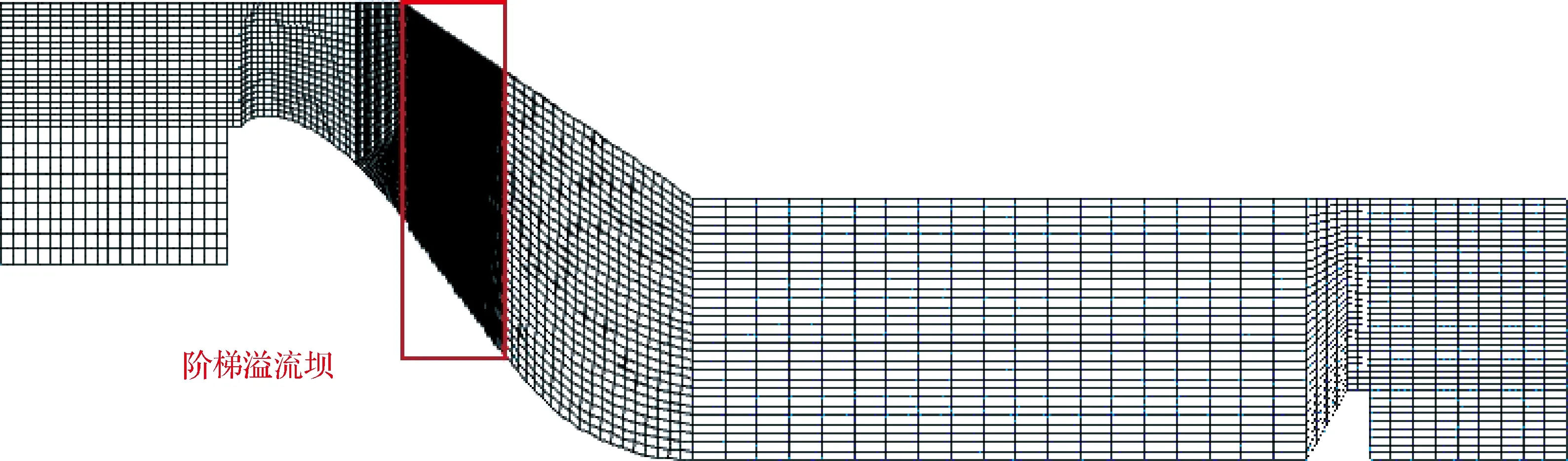
图1 全流场网格划分分布

2.3 边界条件

上游进口边界分为空气进口边界和水流进口边界两部分,空气进口边界条件设置为压力进口,水流进口边界条件设置为速度进口,进口水流流速的模拟值vin=0.406m/s;下游出口边界亦分为空气出口边界和水流出口边界两部分,空气出口边界条件设置为压力出口,水流出口边界条件设置为自由出流,出口水深给定的模拟值hout=0.635m。固壁面均自定义为无滑移边界条件。

2.4 数值模拟验证

为了验证数值模拟的可靠性,对i=10°、h=1m的掺气坎+均匀阶梯的一体化消能工分别进行水工模型试验和数值模拟试验,对比其消力池水深水力指标进行验证。从表1中发现:水深实测值和计算值在消力池的变化规律基本一致,沿程逐渐增加,在桩号0+241.00处,水深达到最大,后有所降低。沿程水深的实测值与计算值的最大误差为6.51%,最小误差为0.32%,平均误差为1.92%,两者数据吻合度高,说明采用该数学方法对模型模拟出的消力池水面线具有较高的准确性。

表1 消力池水深分布

3 计算结果及分析

3.1 压力场

为了分析水流对阶梯溢流坝面的压力分布情况,采用时均压强作为衡量压力的标准,时均压强在阶梯溢流坝面上的沿程分布结果见图2,图2中的压强为水流在14号、17号、20号、23号、26号和29号阶梯内产生的最大时均压强。

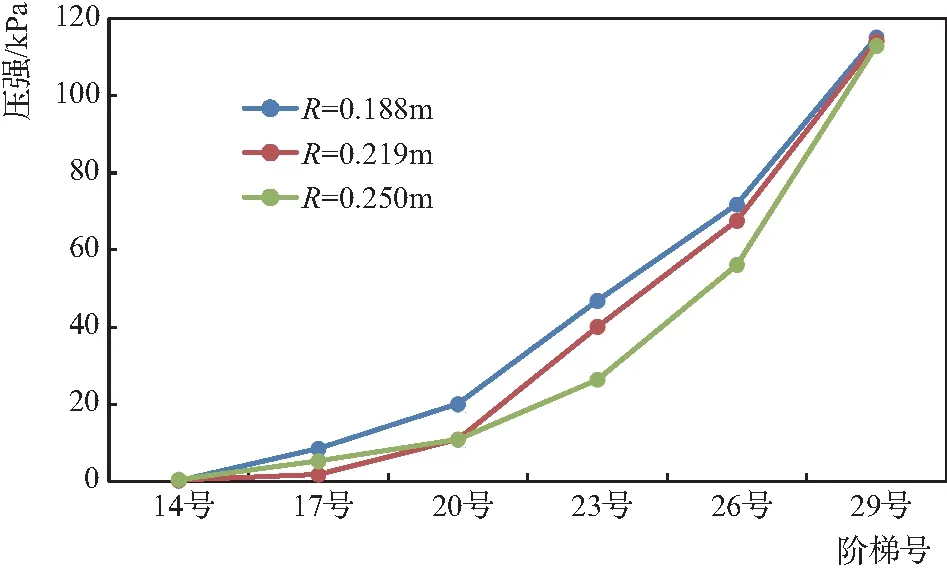
图2 阶梯溢流坝时均压强沿程分布

从图2中发现:三种修圆角形过渡阶梯在阶梯溢流坝面上的时均压强变化基本一致,沿阶梯溢流坝面向下,时均压强逐渐增加,在29号阶梯处,时均压强达到最大。主要是由于水流在跌落至阶梯溢流坝面后,由本级阶梯流向下一级阶梯,势能转化为动能,时均压强逐渐增大。其中,圆角半径为0.188m的方案在阶梯溢流坝面上的最大压强为115.183kPa,当圆角半径增加到0.219m时,最大压强降低到114.182kPa,降低了0.877%;圆角半径继续增加至0.250m,最大压强依然呈现下降的趋势,降低至112.985kPa,相比圆角半径为0.219m的方案降低了1.059%。可见,随着修圆角阶梯的圆角半径增加,时均压强逐渐减小。分析其原因,修圆角形阶梯的圆角半径较大,水流受到的离心力增大,影响了水流的流态,使其更加远离阶梯溢流坝面,使水流更为集中地跌落至下游,从而使水流在阶梯面上产生了较厚的“水垫”,对水流具有缓冲作用,减小了水流对阶梯面的压力,时均压强有所减小。因此,修圆角形过渡阶梯的圆角半径越大,水流对阶梯面的压力越小,时均压强越小,消能效果较好;反之,水流对阶梯溢流坝的压力越大,压强越大,消能效果越差。

3.2 紊动动能分布

紊动动能表征湍流紊动的强弱,是反映水流能量和能量损失的重要因素之一。图3显示的是不同圆角半径的修圆角形过渡阶梯的紊动动能在阶梯溢流坝面上的分布情况。从图3可以看出,各方案的紊动动能在阶梯溢流坝面上的分布规律基本一致,沿阶梯溢流坝向下,水流的紊动动能逐渐增加,在阶梯溢流坝的中下游附近,水流的紊动动能达到最大,这主要是水流沿阶梯溢流坝下泄时的势能转化为动能所致。

为了更进一步分析水流在阶梯内产生的紊动动能分布情况,对不同圆角半径的修圆角形过渡阶梯溢流坝上的第14号、20号、26号阶梯水平面的紊动动能进行对比,图4为各方案在各个阶梯内紊动动能的分布情况,其横坐标为各个阶梯水平面对应的x坐标值,x坐标值越大,说明测点越接近阶梯外侧,测点位于各阶梯水平面以上2mm处。从图4可以看出,在14号阶梯内,随着x坐标值的增加,各方案的紊动动能均增加,且均在阶梯凸角边缘产生的紊动动能最大,20号阶梯、26号阶梯也呈现相同的趋势。与20号阶梯、26号阶梯相比,水流在14号阶梯内产生的紊动动能较大,主要是因为14号阶梯附近为下缘水流在阶梯溢流坝面的跌落区,水流下跌到阶梯溢流坝面,带入较多的气体进入水体,气体与水体接触、碰撞,使紊动动能较大。从14号阶梯到20号阶梯,由于水流与阶梯面碰撞改变了水流的运动状态,在惯性的驱动下,紊动动能有所减小。从20号阶梯到26号阶梯,水流重新达到稳定后向下游展开,紊动动能增大。在14号阶梯内,R=0.188m方案的最大紊动动能为7.266m2/s2,当修圆角形过渡阶梯的圆角半径增大到0.219m时,紊动动能增加到8.048m2/s2;圆角半径继续增大至0.250m,紊动动能继续增加至9.090m2/s2。可见,随着修圆角形过渡阶梯的圆角半径的增加,紊动动能逐渐增大。

分析其原因,圆角半径越大,受圆角半径离心力的影响,在阶梯溢流坝面形成的可掺气空腔容积越大,有利于阶梯面吸卷空气,被吸卷的空气越多,对水流的扰动作用越大,气体与水体之间相互碰撞的次数越多,在此过程中消耗的能量也就越多,因此紊动动能越大,消能效果越好。

4 结 论

a.随着修圆角形过渡阶梯的圆角半径增加,时均压强逐渐减小。

b.修圆角形过渡阶梯的圆角半径越大,紊动动能越大。

c.圆角半径为0.188～0.250m时,增大修圆角形过渡阶梯的圆角半径,有助于提高阶梯溢流坝的消能效果。