自相似流量的长短期记忆网络预测模型研究

李佳男 李琳琳

(1.沈阳理工大学 辽宁沈阳 110159; 2.沈阳开放大学辽宁沈阳 110003)

随着时代的进步，人们对通信网络的需求越来越大，对通信质量的要求也越来越高。在为通信网络设计自适应拥塞控制和主动管理方案上，预测网络流量的行为尤其重要[1]。预测通常依赖于构建随机模型来预测给定历史值的后续时间序列值。传统上，这是通过使用线性模型来实现的。用于时间序列预测的经典线性模型包括自回归（Autoregressive，AR）和自回归滑动平均（Auto-Regressive Moving Average，ARMA）模型等[2-3]。这些模型在大多数报告的情况下适用于平稳时间序列，即统计特性不随时间变化的序列。而通信网络会受到许多外界因素的影响,显示出非线性趋势。这种趋势以及包含的非特定随机因素，很可能会妨碍线性模型的准确预测，所以选择非线性模型更为适合此方面研究。因此，非线性模型的对比选择也成为预测网络流量[4-5]的关键。

1 自相似流量特性与模型选择

测量研究表明：网络流量具有自相似等一系列特性[6]。显著特征就是网络流量中同时存在长程依赖和短程依赖。因此，需要模型来预测具有长期和短期依赖性的流量。而循环神经网络（Recurrent Neural Network，RNN）的记忆功能恰恰符合这一特征,作为非线性模型的同时，RNN 在神经元之间建立联系，与流量相关性特点十分切合，但传统RNN也存在十分严重的问题，即在处理长时间序列时，其梯度在迭代过程中存在趋于0或越来越大[7]的情况，导致网络无法继续训练下去。因此，作为RNN 的一种进化形式，长短期记忆神经网络（Long Short-Term Memory，LSTM）[8-9]更适合网络流量的预测研究。

2 预测模型介绍

2.1 循环神经网络（RNN）

RNN 作为一种经常用来处理时间序列问题的神经网络从结构上如图1所示。

图1 循环神经网络（RNN）结构图

X为输入变量；U、W、V为层间权值矩阵，分别为：输入到隐含层、隐含层到隐含层、隐含层到输出层；St可以看作一种“记忆体”，用来记忆之前时刻的信息；O则为序列的输出。输出0t由当下输入与上一刻记忆共同作用得到。不同于卷积神经网络（Convolutional Neural Networks，CNN）[10]，RNN 中的（U、V、W）固定不变,这在很大程度上减少了训练难度与预估难度。不过，矩阵St 维度容量有限，导致长期记忆受限，即梯度消失，与自相似性不符，进而导致预测效果并不理想[11-12]。

2.2 长短期记忆网络（LSTM）

作为RNN 的变体形式，LSTM 有效地解决了RNN长期记忆的梯度问题，为预测带来了实质性的帮助，更符合自相似流量实际情况，其记忆单元如图2所示。

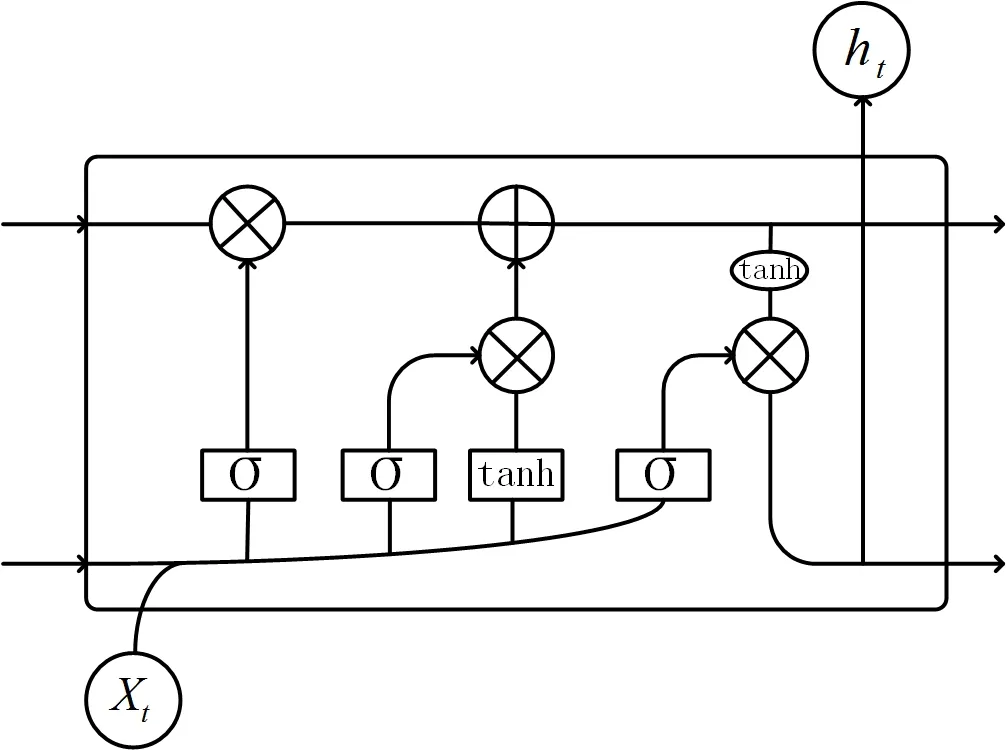
图2 长短期记忆神经网络(LSTM)记忆单元

LSTM 在RNN 上引入了一个细胞状态（cell state）的概念，用来保存长期状态。从图2可以看出，单元间的连接由一条变为两条，短期记忆和长期记忆分别进行记忆。从图中可以看出，记忆单元主要由3 个部分组成，分别为遗忘门、输入门、输出门，这3种门限作用各不相同。遗忘门作用是对是否丢弃之前的隐藏细胞状态h(t-1)给以控制，其计算公式如式（1）所示。

输入门作用是负责处理当前序列的输入问题。其计算公式如式（2）、式（3）所示。

输出门作用是输出t-1 时刻的隐含状态h(t-1)和t时刻的单元状态c(t)。其计算公式如式（4）、式（5）所示。

σ和tanh的数学表达式如式（6）、式（7）所示。

上述所有公式中，Wf、Wi、Wc、Wo、Uf、Ui、Uc、Uo为权值矩阵，bf、bi、bc、bo为偏移量。

3 仿真过程与结果分析

3.1 仿真过程

第一，将ON/OFF 物理模型模拟出的网络。流量作为仿真数据，由于长相关流量具有突发性，故需进行多次模拟，对比后得出较为合适的数据进行训练和测试。

第二，用LSTM针对数据各方面特性进行建模，设置好各部分参数。

第三，将得到的训练集数据输入模型当中，反复模拟，并时刻调整各方面参数，缩小误差，直至达到预测要求，完成训练模型。

第四，将得到的测试集数据输入改进后最终模型中，反复模拟，获取最优结果，并与原数据进行对比，分析预测结果。选用可以反映预测误差实际情况的绝对误差平均值（MAE）进行模型预测精确度评判。

MAE计算公式如式（8）所示。

3.2 参数设置及结果分析

该文数据集由ON/OFF 物理模型模拟产生。通过Matlab 软件设置各项参数进行仿真，主要包括三大分布，设置参数如下：Poisson 分布λ=0.5，指数分布μ=2，Pareto 分布X=0.01，K=1.5,σ=θ=1,速率R=45（p/s）。得到如图3的200 s自相似流量仿真图，图4则为LSTM预测仿真图，图5为预测效果对比图。从图像角度看，仿真图形状几乎一致，反映出的效果达到预期。

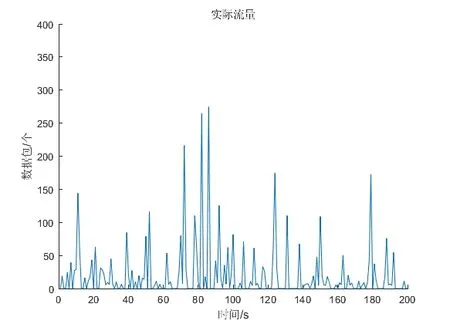
图3 200 s自相似流量仿真图

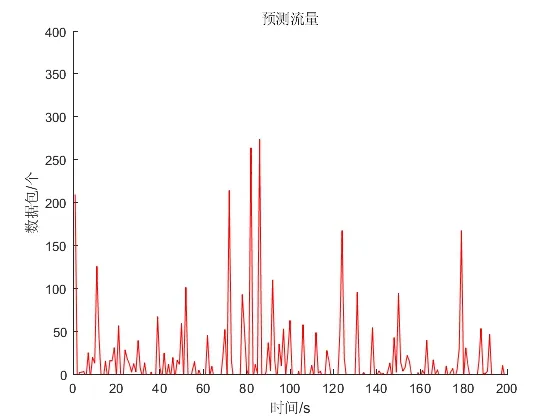
图4 LSTM模型流量预测仿真图

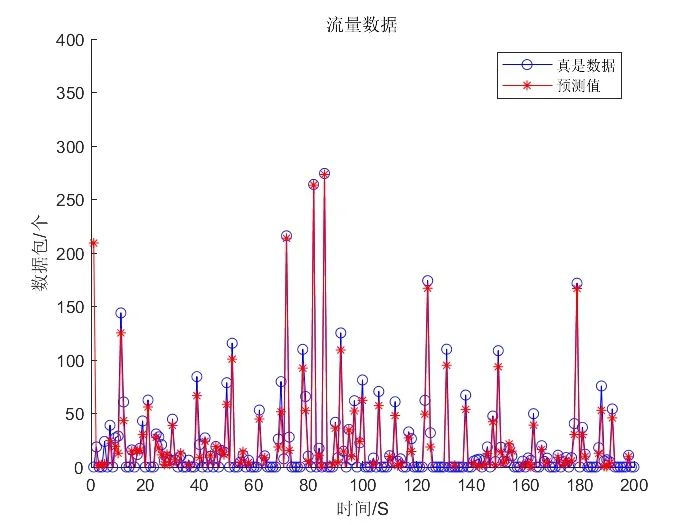
图5 预测结果对比图

通过软件在实际流量仿真图和预测流量仿真图中随机抽取5 组数据进行对比，在横坐标（时间）分别为15 s、42 s、72 s、86 s、179 s 处取其纵坐标（数据包个数），ON/OFF模型产出真实数据包分别为15个、27个、216 个、274 个、171 个。由LSTM 预测模型产出数据包分别对应为14 个、24 个、213 个、272 个、166 个。相对误差分别为6.7%、11.1%、1.3%、0.7%、2.9%，表面上看，在15 s、42 s 时刻误差较高，其原因是因为此时刻原始数据包数较小，此两点误差实际仅有1、3，故用相对误差直接进行评判并不十分准确。故前文提出该文数据方面将由绝对误差平均值进行评判，其函数表达式如式（8）所示，得出预测数据的绝对误差平均值为2.8，远小于实验预设的目标值5。而从图5 中看出的个别时刻误差相对而言大一些，是由于自相似流量本身就具有不确定性、突变性，因而图中起伏看起来较为明显。综上所述，运用长短期记忆网络预测模型对自相似流量进行预测是完全可行的。

4 结语

文章根据网络流量特性选择产生过程较为一致的ON/OFF 物理模型产生自相似流量，并分析其性质特点，对比选择LSTM预测模型对网络流量进行预测，反复实验，不断优化数据。虽然与传统循环神经网络（RNN）相比，LSTM 神经网络作为变体，在结构上相对复杂，但却实实在在解决了RNN梯度以及无法长期等方面的问题，十分契合流量场相关特性，在精确度上也有很大提升。仿真软件选择了MATLAB 平台，结果也证明网络流量的可预测性。下一步计划将其与队列管理进行融合，在可以预测未来流量进入队列的情况下，可以提前做出准备，相信这对网络拥塞控制可以起到重要的作用。