“传球”问题纵横谈

山东省桓台第一中学 苏同安

对于数学问题,不能仅满足于会做或是用了几种方法解出;对于课堂教学容量也不能只是用“题量”或内容的多少,甚至是交流的多少来体现.课堂教学更重要的是在注重过程的基础上产生了多少有价值的“思维量”,是否进行了或“追根求源”或“横纵拓展”的探究活动.下面通过在教学中对一个数学问题的思考和探究来说明这一点.

1 问题呈现

问题甲、乙、丙三人传球,由甲开始发球,并作为第一次传球,经过5次传球后,球仍回到甲手中,则不同的传球方式共有多少种?

下面阐述在课堂教学中,如何引领学生从对问题的各种解决方法入手,由特殊到一般、横向到纵向来进行思考、探究和总结.希望对探究和解决其他数学问题带来一些启迪作用,帮助学生更加深刻地认识数学问题的本质,体悟数学思想方法的价值.

2 几种解法

以下是上述问题的几种解决方法.

方法一：树图列举法.

甲第一次传球是给乙的传球方式(如图1所示), 共5种情况.

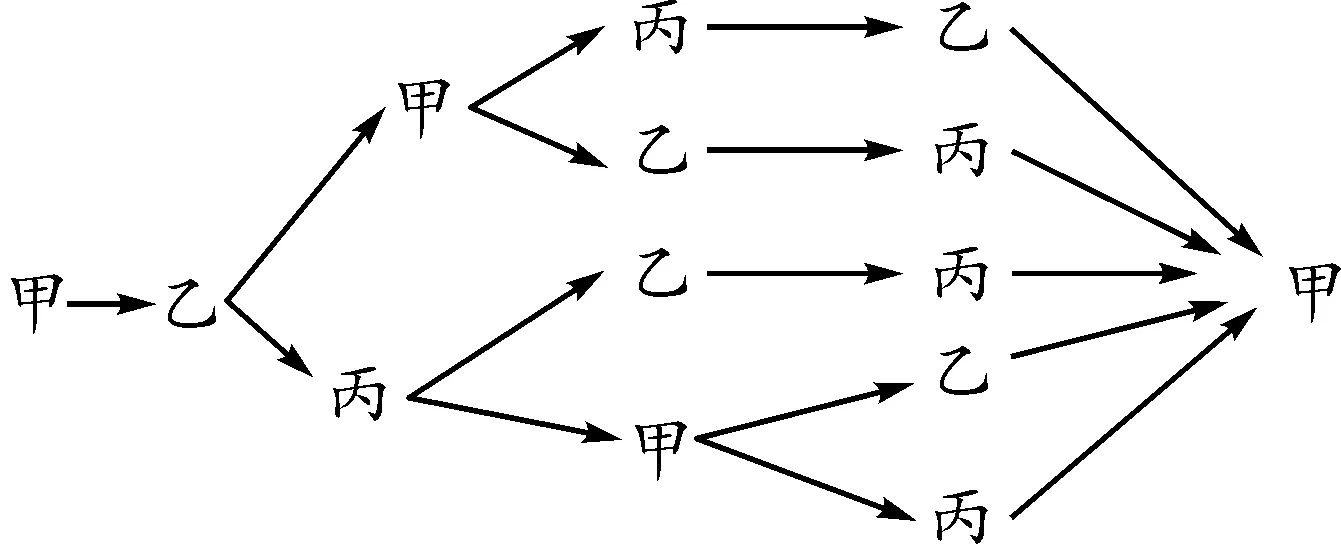
图1

同理,甲若第一次传球是给丙,则同样有5种方式.故所有传球方式共10种.

方法二：分类图解法.

甲、乙、丙三人按图2所示位置站立.

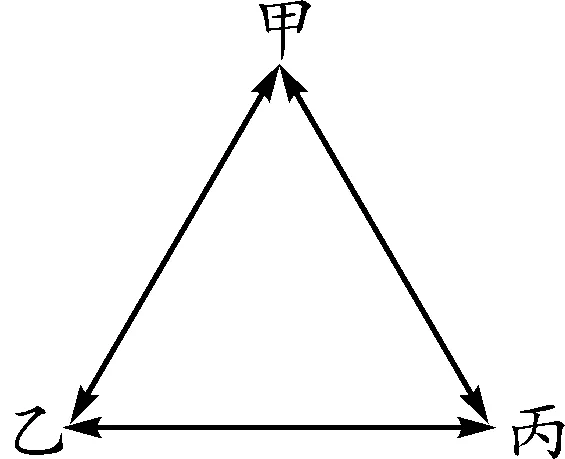
图2

下面列出甲第一次传球是给乙的传球方式,共5种情况,如图3-1,3-2,3-3,3-4,3-5所示.

图3-1

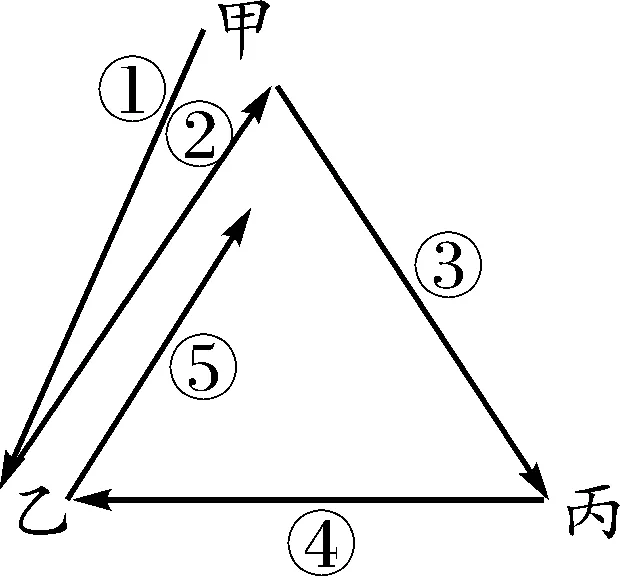
图3-2

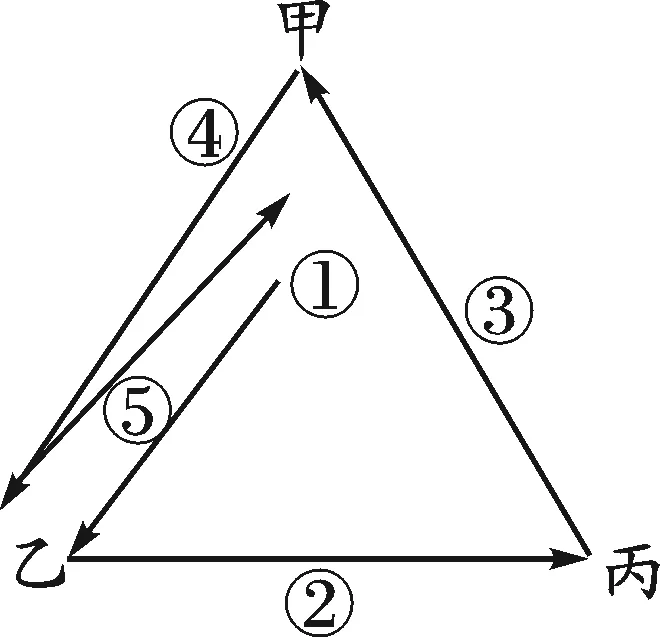
图3-3

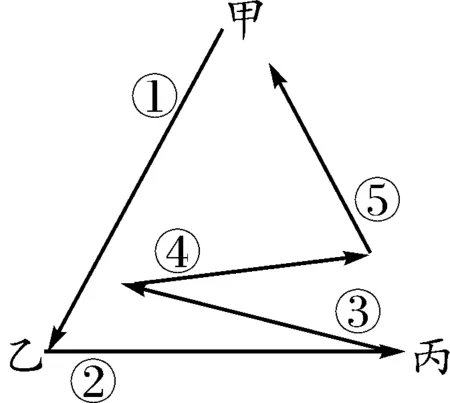
图3-4

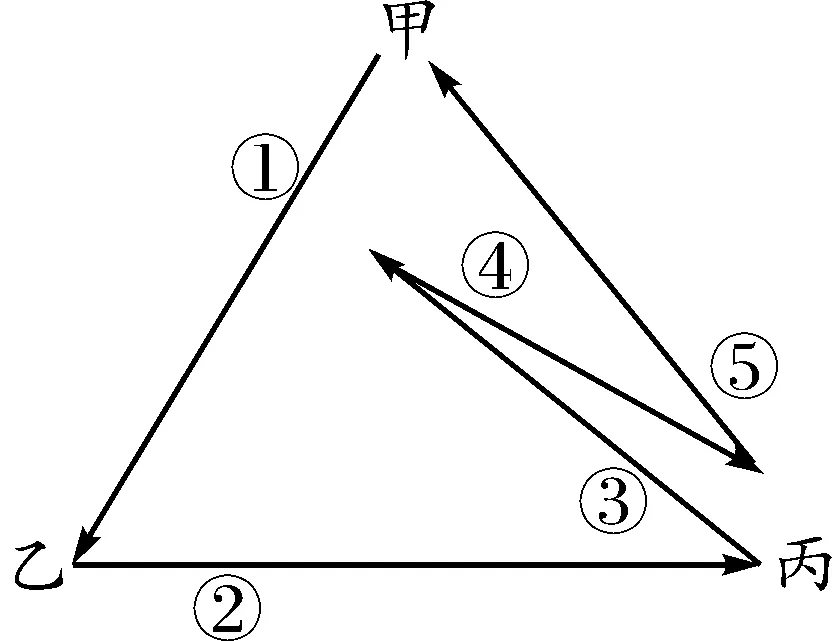
图3-5

同理,甲若第一次传球是给丙,则同样有5种方式.故所有传球方式共10种.

方法三：排列组合法

记“乙”与“丙”为“非甲”,则甲开始传球,经过五次传球,共有六个位置,如图4所示.

图4

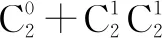
3 横向联系

排列组合问题的“实际背景”可能会多种多样,但很多问题的本质是一样的.关注和探究数学问题的本质,会大大促进数学思维能力、抽象概括能力以及解决问题能力的提高.因此,可利用某些典型问题,引领学生“适当”地进行横向联系,探究一些背景不同但本质相同的数学问题.

涂色问题在如图5所示的六个方格里涂上红、黄、蓝三种颜色,要求相邻两个方格不同色,第1与第6两格均为红色,则涂色方法有多少种?(“第1与第6两格均为红色”与“球回到甲手中”本质相同.)

图5

排数问题用1,2,3这三个数字排成六位整数,要求首位和末位排1,且任意相邻的两个数字不相同,则可以得到多少个不同的六位整数?(“首位和末位排1”与“球回到甲手中”本质相同.)

安排问题甲、乙、丙三人值班六天,每天一人值班,每个人值两天班.其中,第一天和最后一天由甲值班,且相邻两天不能是同一人.则共有多少种不同的值班方式?

(“第一天和最后一天由甲值班”与“球回到甲手中”本质相同.)

对于上述问题,既可运用传球问题中的解法来解决,又可根据此题的情境,生成贴近问题实际的解法.比如涂色问题,可有如下解法:

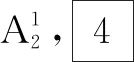
综上可知,共有4+4+2=10种涂色方案.

其他问题,本质相同,就不做详细解答了.

点评：上述给出的几类问题中,有的问题可引导学生编制.这样做不只是为了解几个题,更重要的是让学生通过这个过程,利用不同的背景进一步认识数学知识和数学思想方法的本质,提高数学思维能力、抽象概括能力以及解决问题的能力.

当然，在科研上光是“异想天开”是万万不行的。“异想天开”只是提供一个设想，而设想只是对问题的一个超前、大胆的预测，必须靠实事求是的科学态度和严谨的科学手段加以证明。实现创新突破的覃重军也一再强调自己的“大胆猜想”，是经过了一系列严谨的科学实验才最终得以成功实现的。

4 纵向拓展

上述传球问题中只有3人,传球也只有5次,还应根据学生的实际情况,引领学生将问题“逐步”推广到一般情况,首先将“5次”传球推广到“n次”传球.

拓展问题1甲、乙、丙三人开始传球,由甲开始发球,并作为第一次传球,经过n次传球后,球仍回到甲手中,则不同的传球方式共有多少种?

解析：设经过n次传球后,球在甲手中的不同方法有an种,不在甲手中的方法有bn种.

显然a1=0 , 并且an+bn=2n.

经过n次传球后,球在甲手中,此时有an种方法.这说明第n-1次传球后球没在甲手中,此时有bn-1种方法,再从不在甲手中传到甲手中只有一种途径,即1种方法.

所以bn-1×1=an,即an=bn-1.

又因为an-1+bn-1=2n-1,所以an+an-1=2n-1.

又a1=0 ,则问题转化为求数列的通项公式.

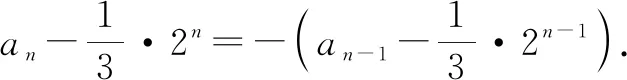
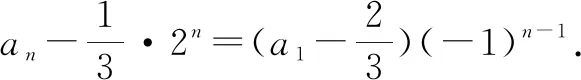
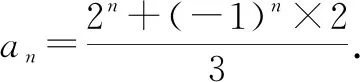
再把问题中的“3人”推广到“m人”,就可把问题纵向推广到更为一般的情况.

拓展问题2有m个人做传球游戏,每个人可将球传给任何一人,由甲开始发球,并作为第一次传球,经过n次传球后,球仍回到甲手中,则不同的传球方式共有多少种?

解析：设经过n次传球后,球在甲手中的不同方法有an种,不在甲手中的方法有bn种.

显然a1=0 , 并且an+bn=(m-1)n.

经过n次传球后,球在甲手中,此时有an种方法.这说明第n-1次传球后球没在甲手中,此时有bn-1种方法,再从不在甲手中传到甲手中只有一种途径,即1种方法.

所以bn-1×1=an,即an=bn-1.

又因为an-1+bn-1=(m-1)n-1,所以

an+an-1=(m-1)n-1.

又a1=0,则问题转化为求数列的通项公式.

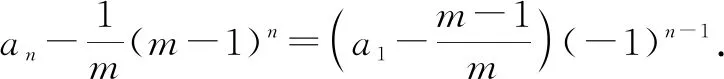
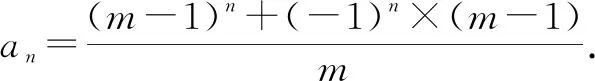
通过对三人传球问题的横向和纵向的思考和探究,既初步认识到了此类数学问题的本质,又感受到了数学知识之间的广泛联系.这对学习数学知识和解决数学问题有较好的启发作用,同时让学生进一步认识到——对待数学“问题”不能只是孤立地去解决,而应该用“联系”和“运动”的眼光去研究它.退,能得到问题的“本源”;进,可拓展出其“一般性”,从而通过“追根求源”或“横纵拓展”的探究活动,来体现思维过程和思想方法的“全景”.从这样的过程中方可体悟出数学的真谛,从而进入神奇的数学世界中——听数与式奏响的神奇韵律,看图与形编织的美丽彩虹.