基于潜在表示的自适应权重多视图子空间聚类算法

刘云祥，王一宾,2

(1.安庆师范大学计算机与信息学院，安徽安庆 246133；2.安庆师范大学智能感知与计算安徽省高校重点实验室，安徽安庆 246133）

0 引言

在处理现实数据的机器学习研究中，研究对象往往由不同方向来源的数据组成，这决定了数据集具有多源性[1]。比如，人类指纹可以由光学指纹仪、热红外采集仪和电容式指纹仪等多种方式途径获取。无监督学习形式的多视图聚类作为多视图学习的一个重要领域，其思想旨在寻找单个视图数据中的底层结构，再学习一个新的统一视图表示，然后在这个视图表示上使用聚类算法，得到最终聚类结果[2]。

子空间聚类假设高维数据集的数据点是由多个低维子空间共同表示，也就是不同数据匹配不同且相应的低维子空间，其作为一种有效的降维方式，在许多聚类问题中起到了关键的作用[3]。因此，研究者们提出了诸多子空间聚类方法来探寻底层子空间。多视图数据中，多个视图特征信息丰富了每个数据点，聚类效果得到提升。Gao 等人[4]提出多视图子空间聚类，对不同视图的子空间表示进行聚类，同时使用一个共同聚类结构确保不同视图之间的一致性。多视图数据的多样性和互补性原则作为处理多视图信息的关键因素，潜在表示能更全面地描述数据本身，充分体现出多视图互补性信息[5]。研究者们引入潜在表示来探索多视图数据存在的互补关系，在此基础上改进了子空间聚类。Zhang 等人[7]提出潜在多视图子空间聚类算法[6]和广义潜在多视图子空间聚类算法，两个算法均假设多个视图有一个统一子空间潜在表示，利用潜在表示学习邻接矩阵并进行谱聚类得到最终聚类结果。低秩约束和稀疏约束可以更好地获得数据的全局和局部结构，Wang等人[8]联合低秩表示和稀疏表示到子空间自表示矩阵中，通过谱聚类算法进行最终聚类。即便如此，仍忽略了视图之间存在的差异性以及视图质量的参差不齐。不同视图分配合理权重能提高聚类效果，利用视图自表示矩阵与统一表示矩阵之间距离的反比关系，为每个视图分配合理的权重[9-10]。Kang 等人[11]利用反距离加权法融合多视图信息，并利用谱聚类进行最终聚类。Xia 等人[12]在此基础上为视图表示添加低秩稀疏约束，进一步提高聚类效果。

结合以上论述内容，本文提出潜在低秩稀疏表示的自适应权重多视图子空间聚类的算法。其主要贡献是：学习多视图信息的潜在表示，并施加低秩稀疏约束，尽可能获取多视图数据的互补信息及全局、局部结构；同时引入自适应权重方法，在构建统一邻接矩阵过程中为不同视图分配合理的权重，也可以降低视图噪声对于聚类结果的影响，并在一个框架内共同优化。在6个不同数据集中的对比实验结果证明，该算法具有一定的有效性。

1 模型与方法

1.1 低秩稀疏约束的多视图子空间聚类

其中，α1和α2分别作为低秩约束和稀疏约束的平衡系数。通过式(1)计算相似度矩阵，并通过谱聚类[13]获得最终聚类效果。

1.2 潜在低秩稀疏表示的多视图子空间聚类

假设不同的视图都来自一个共享的潜在表示h。具体地，不同视图下的数据点可以由共享的潜在表示通过对应的映射{P(1),P(2),…,P(v)}来描述。对子空间结构添加低秩约束和稀疏约束。并且考虑到数据集广泛存在噪声和子空间重构的误差。同时为降低目标函数优化复杂度，将潜在表示和子空间表示对应的误差列垂直连接在一个矩阵，它将强制Eh和Er的列具有共同一致的幅度值，即减少一个平衡参数。统一目标函数改写为：

式(2)中，λ1＞0,λ2＞0，Eh、Er分别代表潜在表示的构造误差和潜在表示中存在的噪声，X=[X(1),X(2),…,X(v)]T代表相对应的多视图数据点，P=[P(1),P(2),…,P(v)]T代表重构模型。第一项用于确保学习到的潜在表示形式H 和与不同视图相关联的重构模型P(v)有利于重构观测结果；第二项用于惩罚多视图子空间潜在表示中的重构误差。其次，前两项上的l2,1范数是一个矩阵块范数，它比F 范数更具有鲁棒性。

1.3 潜在低秩稀疏表示的自适应权重多视图子空间聚类

自适应权重方法可以很好解决数据集中存在低质量、有噪声的视图问题。方法基于两种直观的假设[11]：1)每个视图的自表示矩阵Z(v)均对共享表示矩阵Z产生扰动；2)接近共享表示矩阵Z的视图应该被赋予一个较大的权重。使用一组有意义的不同权重来衡量每个视图的重要性。基于上述，共识图Z可以表示为：

其中，图拉普拉斯矩阵为L=D-W，对角矩阵D是dii=度矩阵，W为邻接矩阵，W=(Z+ZT)/2。ωv是各视图的自适应权重，可以反映出视图的重要度，这里采用反距离加权法求解[6]：

其中，F是聚类指示矩阵，γ为谱聚类的平衡参数，当γ足够大使秩约束rank(L)=n-c得到满足。

结合式(2)和式(5)结合最终得到最终目标函数为：

2 模型求解

对于式(6)的联合优化问题，因最终模型中各变量相互影响，多变量问题求解难度大。所以这里利用增广拉格朗日乘子交替方向最小化(ALM-ADM)进行有效分步优化。

在目标函数中引入辅助变量J1、J2、J3，于是有以下等价的问题：

定义L(P,H,Eh,Er,Z,J1,J2,J3)为式(7)的增广拉格朗日函数,可得：

其中，Y1、Y2、Y3、Y4、Y5是拉格朗日乘子，，μ是正的惩罚标量。基于此，有以下几个子问题：

1)固定其他变量，关于P的函数表示为：

2)固定其他变量，关于H的函数表示为：

求关于H的导数，并设置导数为0，有：

方程(17)是一个西尔维斯特方程，可以直接通过巴特尔斯·斯图尔特算法求出H的闭式解[16]。

3)固定其他变量，子空间重构误差矩阵E更新为：

4)固定其他变量，拉格朗日函数J1、J2、J3利用奇异值阈值算子可以有效地解决该子问题：

5)固定其他变量，拉格朗日乘子按比例更新[18]为：

6)固定其他变量，关于Z(v)的项求导并令导数为0，有：

8)固定其他变量，关于F的函数表示为：

F的最优解由L中c个最小特征值相应的c个特征向量得到。

整体目标函数在优化过程中，如果达到最大迭代次数200 或Z的相对变化小于10-3，或‖X -PH-Eh‖∞＜ε,‖H -HZ-Er‖∞＜ε,‖J1-Z(v)‖∞＜ε,‖J2-Z(v)‖∞＜ε,‖J3-Z(v)‖∞＜ε，即达到收敛条件，得到子空间的共享表示矩阵Z可以计算出统一邻接矩阵W，最后进行谱聚类得到聚类结果。

3 实验及结果分析

3.1 数据集

为了评估所提算法的有效性，实验总共选择了6个在多视图聚类中普遍使用到的公开基准数据集。数据集的基本信息如表1所展示。

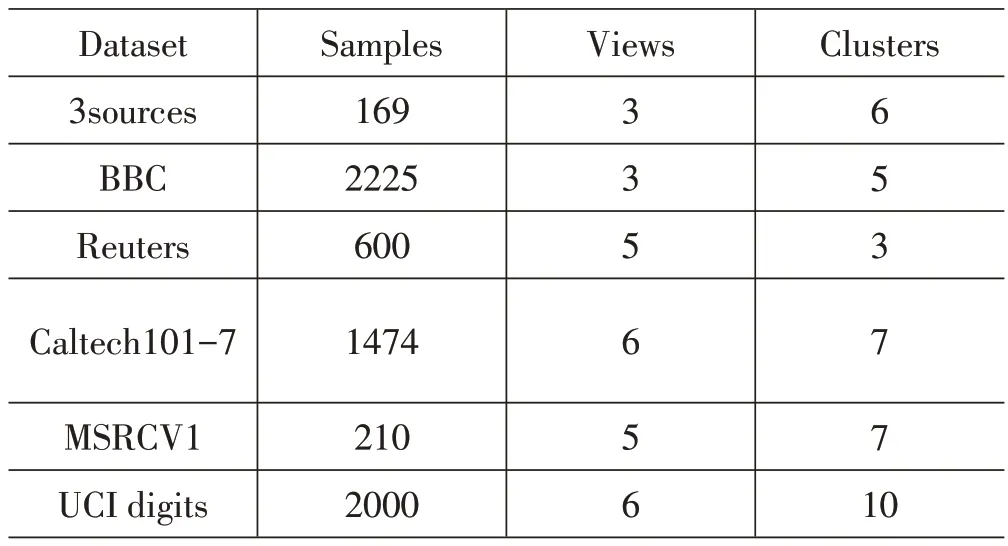
表1 数据集的统计数据

3.2 对比算法与评价指标

为了全面评估所提算法的有效性，实验过程中采用5个经典的单视图聚类和目前多视图聚类领域中的代表性算法作为对比算法。包括：SC (Spectral Clustering)[19]、LRSSC (Low-Rank Sparse Subspace Clustering)[8]、MVSC(Multi View Subspace Clustering)[4]、MGFSC(Multi-Graph Fusion Spectral Clustering)[11]、gLMSC(Generalized Latent Multi-view Subspace Clustering)[7]。

实验选取4项常见的聚类外部评价指标来对所有算法综合对比性能，包括聚类精度(Cluster Accuracy，ACC)，归一化互信息(Normalized Mutual Information，NMI)，F 值(F-measure)和调整兰德系数(Adjusted Rand index，ARI)。指标数值越高，聚类效果越好。

3.3 实验结果与分析

对所有数据集进行归一化处理，并在数据集上取潜在表示矩阵H的维度D固定为100。实验重复10次并计算指标结果的均值和标准差。3sources、BBC、Reuters、Caltech101-7、UCI digits、MSRCV1 的λ1、λ2、β、γ分别取{10,0.1,10,10E-6}、{10,1,10E+7,10E-5}、{0.1,0.01,1000,0.01}、{10,0.1,0.1,10E-7}、{10,0.1,1,10E-4}、{100,0.01,10E+7,10E-5}。表2～表5 给出评价指标结果，用粗体表示最好的结果。

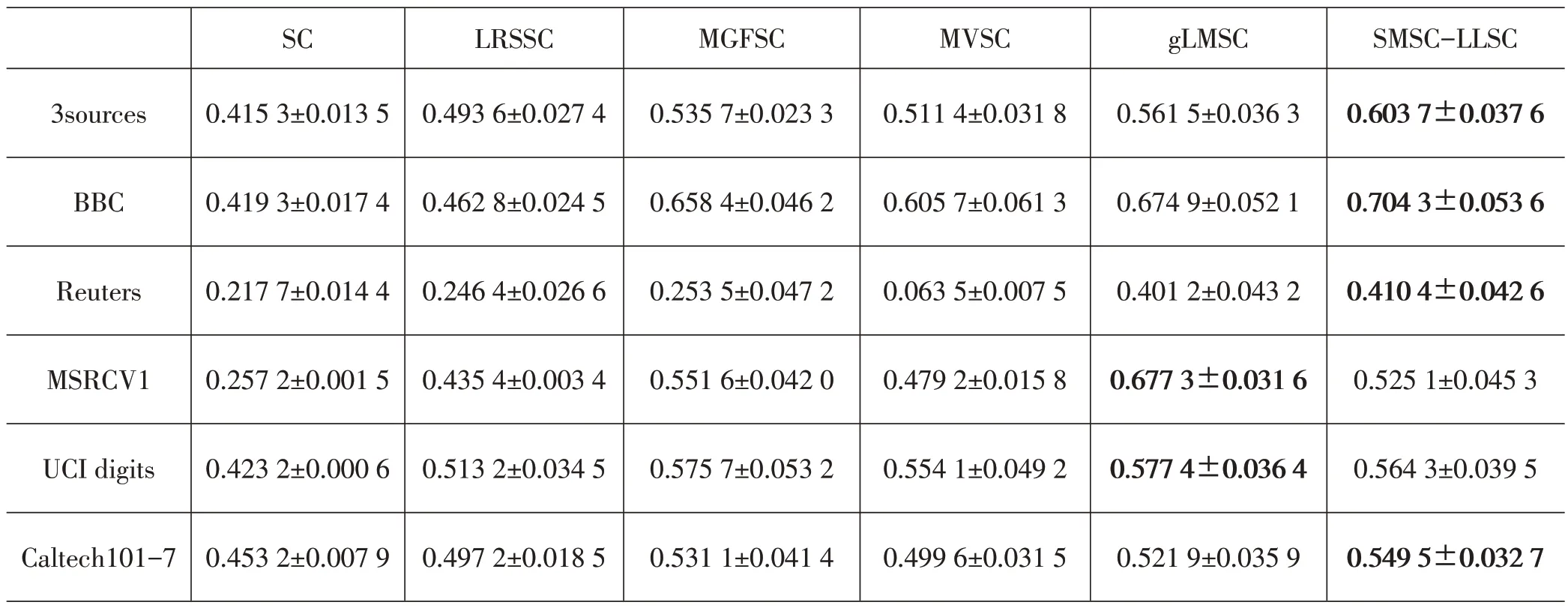
表3 各算法在6个数据集上的NMI指标

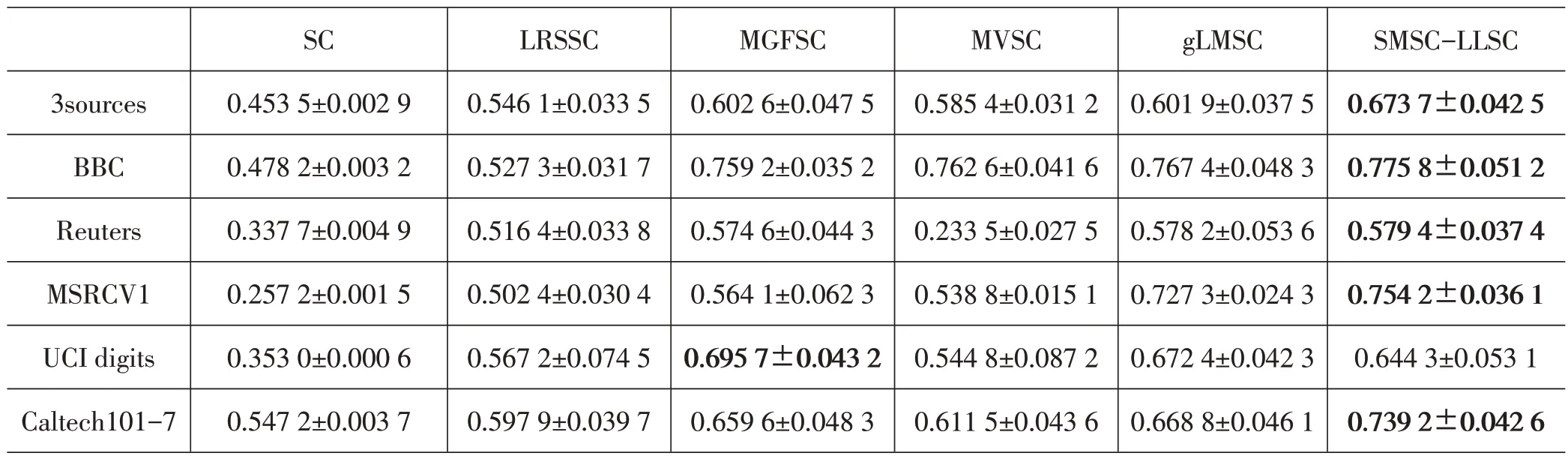
表4 各算法在6个数据集上的F-measure指标

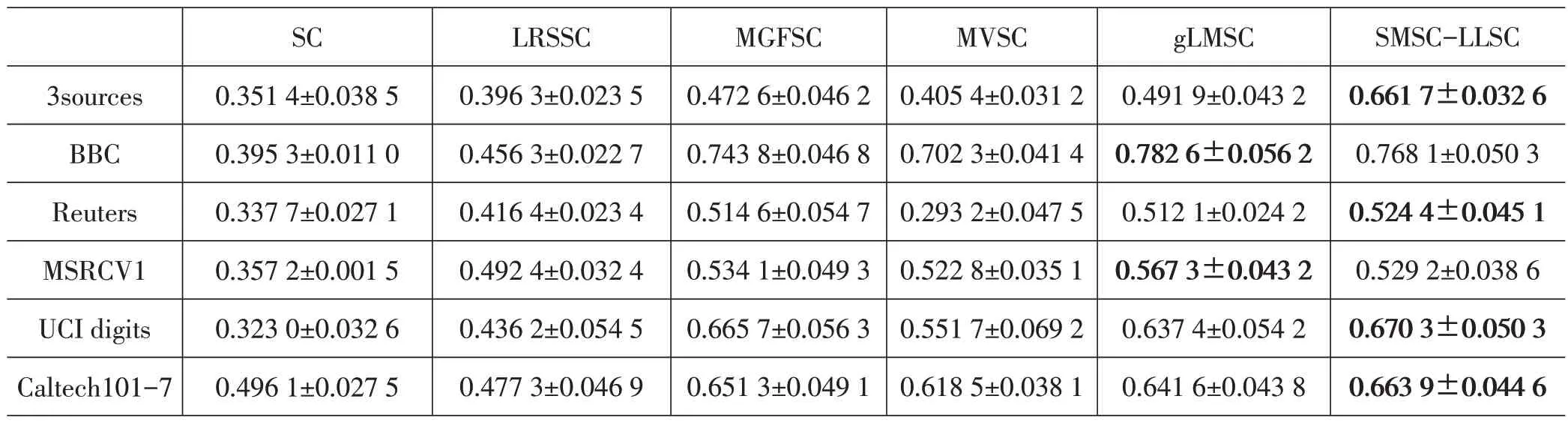
表5 各算法在6个数据集上的ARI指标

由表2～表5可见，算法SMSC-LLSC在6个不同数据集上获得较优结果。相比SC、LRSSC在单一视图上的聚类性能，可以看出，其他基于多视图数据的算法会产生更好的聚类结果。LRSSC 利用了低秩约束和稀疏约束之间的互补，在聚类效果上普遍优于SC，可以看出添加低秩稀疏约束可有利于聚类效果提升。相比于MVSC，SMSC-LLSC在5个数据集中全面占优，这是由于SMSC-LLSC 利用多视图子空间的潜在表示挖掘多视图之间的互补性信息，数据集得以更全面的描述。在3sources 数据集下的实验结果，可以看出，SMSC-LLSC 比先进的次优算法gLMSC 在2 个重要指标ACC 和NMI 上分别提高约1.4%和4.2%，这表明在学习潜在子空间表示的基础上，为视图添加自适应权重，以及对视图子空间的潜在表示添加低秩稀疏约束的操作具有显著意义。

3.4 统计假设检验

为了方便直观展现SMSC-LLSC 算法与其他5 个算法在6个数据集上的聚类性能差异。选用Nemenyi统计假设检验，拿临界值(Critical difference，CD)与对比算法在6个数据集上聚类指标的平均排名作对比，CD值可以通过式(19)计算得出：

其中，α=0.05,K=6,N=6,qα=2.850,CD=3.0784。图1 显示了各算法在4 个指标上的比较。其中，所有算法综合性能从左到右逐渐下降，从图1所示的结果中可以得出结论，SMSC-LLSC 在所有方法中排名第一，算法SMSC-LLSC具有一定的性能优势。

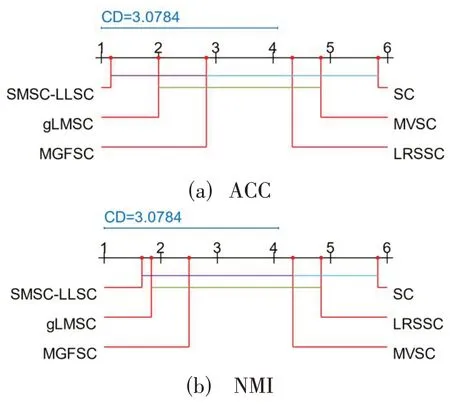
图1 算法的性能比较

4 结束语

针对多视图聚类问题，本文提出潜在低秩稀疏表示的自适应权重多视图子空间聚类算法。算法学习多视图数据子空间的潜在表示以更好地获取多视图数据中一互补性信息，并使潜在表示矩阵具有低秩稀疏特性；同时为不同视图匹配自适应权重，即便低质量视图存在噪声时，也能有效降低对最后聚类结果的负面影响，使聚类结果更准确。并在一个框架内共同优化。在6个不同数据集上的指标结果及统计假设检验均表明本文算法具有一定有效性。