轴压比对混凝土框架结构屈服机制的影响分析

杨 阳

（中铁合肥建筑市政工程设计研究院有限公司，安徽 合肥 230000）

1 模型说明

案例结构模型处于8 度、1 组、Ⅱ类场地，混凝土框架结构二级抗震，规范要求框架柱的轴压比不得大于0.75。因混凝土框架柱的强度等级不得使用低于C25的混凝土，所以模型中设定框架柱的轴压比限值为0.75。

1.1 分析模型

结构设计软件为PKPM，模型结构层高3.6m，共3层，柱之间跨距6m，2×3 跨，框架柱的混凝土强度为C30，截面尺寸为500mm×500mm，框架梁截面尺寸为200mm×500mm，结构板的厚度为110mm。荷载布置如下：二层、三层楼面恒载为5kN/m2，活载为2.0kN/m2，填充墙自重按10.54kN/m 作用在框架梁上；屋面恒荷载为5.8kN/m2，恒荷载为0.5kN/m2，女儿墙自重按3.0kN/m 作用在屋框梁上。对同一模型，更改混凝土强度，得到了M1-M6 模型，最大轴压比如表1 所示。

表1 不同等级混凝土下的最大柱轴压比umax

从表1 中可以发现，在混凝土强度提升的情况下，柱的轴压比不断下降，从C20 的0.75 降到C50 的0.31。通过前人研究可知，轴压比大于0.75 后，无法有效进行强柱弱梁的设计，而小于0.3 时，能有效获得“强柱弱梁”的屈服机制。文章以0.31-0.75的区间为研究对象，分析轴压比达到何种数值后，结构将丧失“强柱弱梁”机制。

1.2 输入地震加速度时程选择

进行分析前，应确定地震动的各项参数，表2 是本次分析中对地震动的参数取值。因模型M1-M6 的周期相近，均为0.65s 左右，考虑到结构在震动过程中会由弹性转化到弹塑性阶段，相应周期也会增加，所以需要地震波反应谱处于结构自重周期的1-1.5 倍区间内，经过多次比较，本次研究选用的地震波为NGA1768-360。

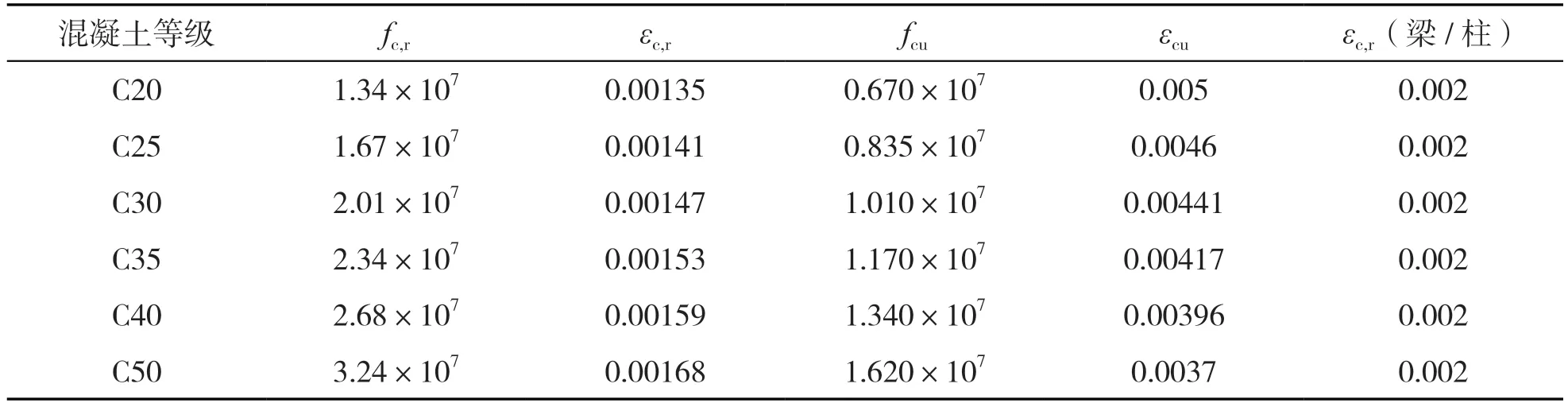
表2 混凝土参数取值

1.3 分析方法

为保证分析的合理性，文章从以下几个方面进行处理：

1.使用不同分析软件分别建模计算，相互校核结果。

2.根据受力特点的差异，对不同构件采用不同的单元进行模拟，并建立合理的本构模型。

3.在对大震作用下的分析时，要求最大弹塑性层间位移不得超过1/50。

2 建立模型

2.1 单元选择

文章所用模型为ABAQUS 和ETABS 两种，以纤维截面单元对梁柱进行模拟，以Shell 单元对结构板进行模拟，以双折线模拟板中的钢筋层。

2.2 材料定义

混凝土参数的设置如下[1-4]：混凝土的轴心受压强度为fc,r、极限受压强度为fcu，峰值压应变为εc,r，极限压应变为εcu，钢筋的屈服应变为εs,y。表2 为混凝土的各种参数取值。

2.3 模型对比

为了校核有限元分析模型的正确性，对比ABAQUS和ETABS 的模态分析结果，在两个程序中分别建立了模型。

3 分析结果

3.1 结构动力特征

以第一个模型为例，分析两种软件的计算结果，包括振型、周期和模型总质量[5-9]，相关结果列入表3进行对比。可以发现，两个软件计算模型的动力特征相近，表明采用任何一个有限元模型计算的结果都是正确的，具有较高的可信度。

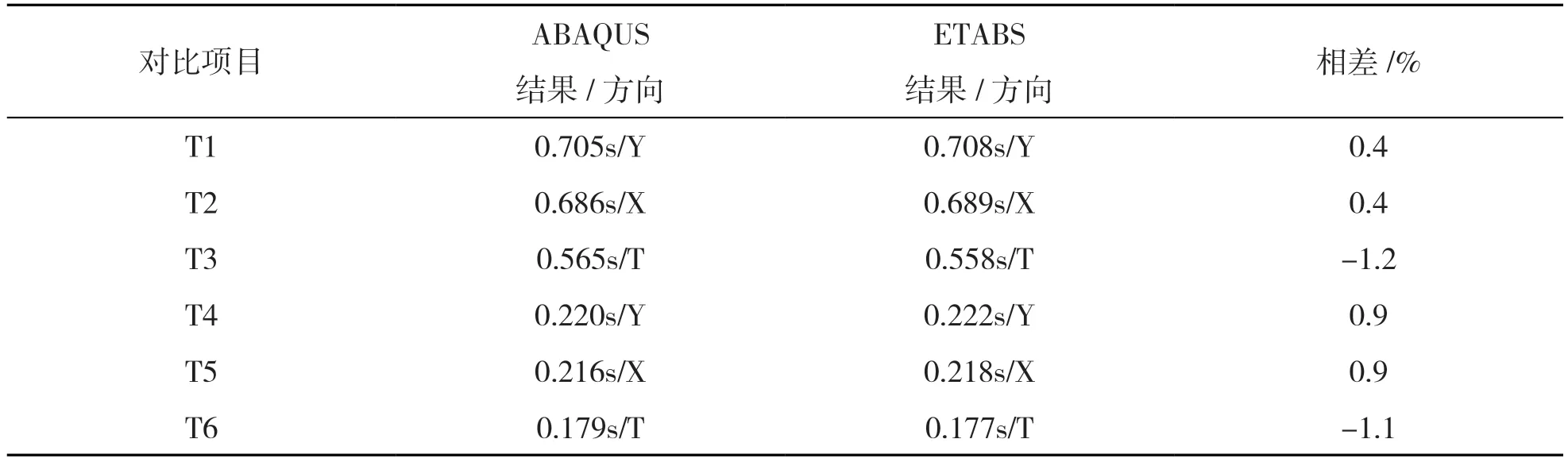
表3 结构动力特征对比

3.2 塑性铰出铰顺序及分布

ABAQUS 计算之后，能够方便快捷查询计算结果。通过设置结果显示，可以查询各个位置塑性铰的发生情况。以模型M1 来做说明，图1 中的圆点即为结构在经过时程分析之后的塑性铰位置图，为方便显示，隐藏了结构中的板单元构件。

图1 塑性铰出现位置

为了分析结构在不同轴压比状况下如何实现“强柱弱梁”的屈服机制，需要得到结构中塑性铰出现的先后顺序，进而分析出梁柱共同作用的机理。因结构中，轴压比最大的两根柱位于B轴，所以取B轴线的框架（简称B 榀框架）作为考查重点进行分析，通过程序中的纤维截面状态变量的时程输出数据查看不同的塑性铰出现的位置，通过与不同塑性铰出现的时间相结合。

图中的数值根据大小分别显示了塑性铰出现时间的先后，其中，数字1 表示在时程分析进行到10s～15s的时候出现的塑性铰；数字2 表示时程分析进行到15s～ 20s 的时候出现的塑性铰；数字3 表示时程分析进行到20s～25s 的时候出现的塑性铰；数字4 表示时程分析进行到25s～30s 的时候出现的塑性铰。可以发现，塑性铰出现的位置和先后顺序，总结起来可以推断出如下结论：

1.轴压比越大的结构塑性铰越多，且塑性铰多易发生在柱子的端部，对结构的抗震效果不利。控制柱的轴压比可减少塑性铰的数量和位置[10-13]。如模型M1和M2 的轴压比较大，柱端产生了较多的塑性铰，而模型5 和6 因轴压比较小，柱端的塑性铰就比较少。

2.在轴压较大的情况下，柱端和梁端的塑性铰出现的概率比较接近，结构容易丧失竖向承载力而发生破坏，但当轴压比变小后，梁端的塑性铰压先于柱端产生，可以有效提高结构的耗能能力，保证竖向构件的安全性，确保结构不会过早发生倒塌现象。

3.因框架柱的轴压比降低，柱端塑性铰出现数量减少显著，且出现时间更加退后，而梁端则多在时程分析开始后就会出现，在时间上先于框架柱进入弹塑性状态，说明较低的轴压比可以更好地实现“强柱弱梁”的机制。

4 结论和建议

通过对同一结构采用不同的混凝土等级，实现柱子的不同轴压比，在分析中可以做到单因素的对比，实现结构的受力状态和受力分配的相同。通过弹塑性动力时程分析，较好地考查整个地震动输入过程中结构梁柱单元的出铰大小、分布及次序来分析“强柱弱梁”机制实现情况。

1.随着轴压比的降低，柱端塑性铰出现的更晚、更少，而梁端塑性铰出现得更早、更多，也就是说框架结构中“强柱弱梁”屈服机制实现得更好。

2.虽然M1 和M2 结构的层间位移角满足规范要求，但是其并不能保证“强柱弱梁”屈服机制的实现。

3.根据本文研究，建议将二级框架柱轴压比适当降低，可以更好地保证“强柱弱梁”屈服机制的实现。