广义后缀树的概念生成算法
林志鸿,王李进,吴清寿
(1.湄洲湾职业技术学院 信息工程系,福建 莆田 351111;2.福建农林大学 计算机与信息学院,福建 福州 350002;3.武夷学院 数学与计算机学院,福建 武夷山 354300;4.智慧农林福建省高校重点实验室(福建农林大学),福建 福州 350002)
形式概念分析 (formal concept analysis,FCA)是Wille[1]提出的用于描述对象与属性之间关系的数学理论,其中概念的生成和概念间的关系构建是热点的研究问题。概念能够反映对象集合和属性集合的最大对应关系,可用于有效表达具有不同属性集合所对应的对象聚合情况。概念的这种特性在不同领域得到较为广泛的应用,如文本挖掘[2],知识表示度量[3],关联规则研究[4]和大规模全局协同进化优化[5]等。
已有的概念生成算法中,经典的算法有Ganter 等[6]提出的基于闭包算子扩展求全部概念的NextClosure算法和Godin 等[7]提出的渐进式概念生成算法等。近几年,研究人员提出一些新的概念格构建方法,如窦林立等[8]提出的利用极大完全子图及其导出子图生成概念格的方法,为概念构造提供新的思路。蔡勇等[9]根据概念外延长度将概念分层,进而实现分层并行搜索概念的父子节点,提高概念构建速度。Zhang 等[10]提出FastAddExtent 算法,其通过减少概念之间的无效比较实现概念格的快速构建。
在离散属性的数据集上,广义后缀树有着广泛的应用,如文本检索、信息聚类、网络社区发现等[11,12]。广义后缀树的构造方法较为成熟,具有线性的时间复杂度[13],可有效提高算法的整体效率。如邹凌君等[11]用广义后缀树提取出完全二分团,基于完全二分团实现二分网络的社区划分,算法具有较好的运行效率。
提出一种基于广义后缀树的概念生成算法(generalized suffix tree based concept generation algorithm,GSTCG),首先利用Ukkonen 算法[13]将对象的属性及其后缀序列构建为广义后缀树,再利用相关规则得到候选的形式概念,经过交叉扩展并删除冗余的候选概念后得到形式背景的全部概念。
1 基础理论
1.1 概念格基础理论
定义1形式背景K 是一个三元组K=(O,A,R),其中O 是对象集合,A 是属性集合,R 是集合O 和A之间的关系,即R⊆O×A。通常,将形式背景简称为背景。对于o∈O,a∈A,(o,a)∈R 表示对象o 具有属性a。背景可以用一个二维表表示,表中第一列和第一行分别是对象集合和属性集合,行列交叉处的“×”表示该行对象具有该列属性。
定义2对于背景K=(O,A,R),若X⊆O,Y⊆A,定义操作为:
其中:f(X)表示X 中所有对象的共同属性集合,g(Y)表示具有Y 中所有属性的对象集合。
定义3对于背景K=(O,A,R),若X⊆O,Y⊆A,且X,Y 满足f(X)=Y,g(Y)=X,则二元组(X,Y)是一个形式概念(简称概念),其中X 称为概念的外延,Y 称为概念的内涵。
一个形式背景的示例如表1 所示,其中对象集合O={1,2,3,4,5}和属性集合A={a,b,c,d}。
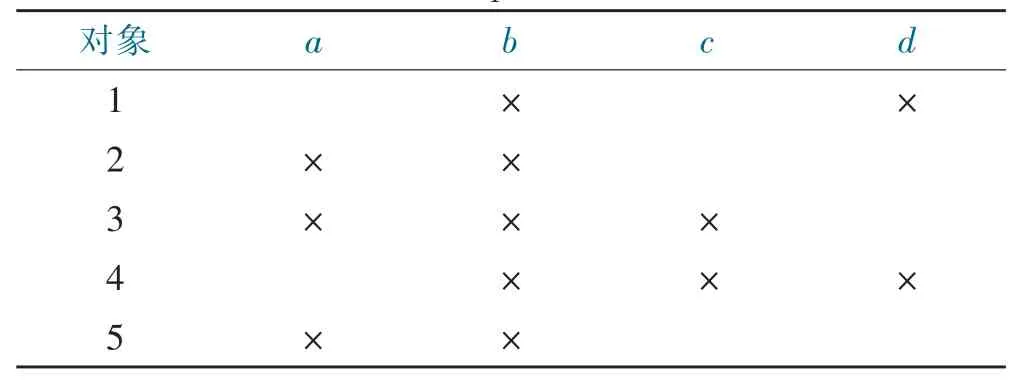
表1 形式背景示例Tab.1 The example of formal context
令X={3,4},则f(X)={b,c},令Y={b,c},则g(Y)={3,4}。因为f(X)=Y,g(Y)=X,所以二元组({3,4},{b,c})是一个概念。令X={2,3},则f(X)={a,b},令Y={a,b},则g(Y)={2,3,5}。因 为f(X)=Y,g(Y)≠X,所以二元组({2,3},{a,b})不是一个概念。
1.2 广义后缀树
表1 所示的形式背景中,对象o3的属性序列为{a,b,c},则其属性序列有以下后缀:{b,c},{c}。利用字典树Trie 对以上属性序列及其所有后缀进行存储,则该树称为后缀树。将一个背景中所有对象的属性序列及其后缀组织为一棵Trie 树,称该树为广义后缀树。本文中广义后缀树上的节点组织形式为二元组(对象集合,属性集合),其表示从根节点出发到达该节点的的对象集合,以及对象集合所对应的属性集合。显然,广义后缀树中的节点的表示形式与形式概念有着极为密切的关系。
2 基于广义后缀树的概念生成算法
形式概念分析中的概念生成任务需要找到全部的概念,提出一种基于广义后缀树的概念生成算法,其主要思想为:利用高效率的后缀树构建算法快速得到候选概念,由候选概念扩展得到全部概念,再对扩展概念中的冗余概念进行处理。
步骤1由形式背景得到所有对象的属性序列及其所有后缀。
以表1 中的形式背景为例,各对象(此处对象用oi表示)对应的属性序列及所有后缀如下。
步骤2根据步骤1 中的所有属性序列及后缀构建广义后缀树,如图1 所示。
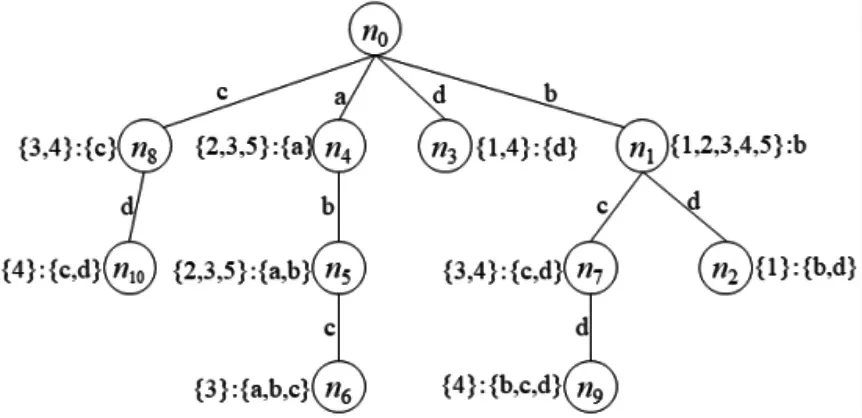
图1 广义后缀树Fig.1 Generalized suffix tree
图1 中广义后缀树的每条边对应一个属性,每个节点表示一个候选概念。候选概念包括两个部分,一个是从根节点到当前节点路径上的所有属性,另一个是包含对应属性集合的对象集合。如节点n7,从根节点n0到n7的路径上有两条边,边所代表的属性分别为{b}和{c},表示n7包含两个属性{b,c}。又因为对象o3中的属性序列的后缀{b,c}和o4中的属性序列{b,c,d}的前缀都是{b,c},所以有n7=({3,4}:{c,d}),其中{3,4}表示对象o3和o4。
另外,由压缩字典树理论和形式概念的定义可知,当具有父子关系的两个节点都只有一个孩子节点且节点所代表的候选概念具有相同的对象集合,则可将这两个节点压缩为一个节点,且边所代表的属性为原来两条边的属性的并集。
如节点n4和n5是父子节点,且都只有一个孩子节点,n4和n5所代表的候选概念的对象集合都是{2,3,5},可将n4和n5两个节点进行合并,合并后的候选概念为({2,3,5}:{a,b})。因图1 中满足节点压缩的只有n4和n5,其他的都不满足条件,所以将图1 中节点压缩后得到如图2 所示的广义后缀树。

图2 压缩后的广义后缀树Fig.2 Compressed generalized suffix tree
图2 中的广义后缀树包含9 个候选概念:n1=({1,2,3,4,5}:{b});n2=({1}:{b,d});n3=({1,4}:{d});n4=({2,3,5}:{a,b});n5=({3}:{a,b,c});n6=({3,4}:{c});n7=({3,4}:{b,c});n8=({4}:{c,d});n9=({4}:{b,c,d})。
由广义后缀树产生的候选概念需要经过系列处理后才能得到最终的概念。
规则1对于ni,nj∈N,i≠j,若f(ni)=f(nj),则将ni与nj进行合并,合并后的候选概念nk=(f(ni),g(ni)|g(nj))。其中,N 是候选概念集合,f(ni)表示候选概念ni的对象集合,g(ni)表示ni的属性集合。
步骤3根据规则1 合并对象集合相同的候选概念。
步骤2 产生的候选概念中,n6与n7的对象集合相同,但其对应的属性集合不相同。根据形式概念的定义,上述候选概念不可能同时存在,所以根据规则1进行合并处理。与上述情况相同的还有n8与n9。
经过步骤3 得到的结果如下:
规则2对于ni,nj∈N,若f(ni)∩f(nj)≠φ,则(f(ni)∩f(nj):g(ni)∪g(nj))也是候选概念。若g(ni)∩g(nj)≠φ,则(f(ni)∪f(nj):g(ni)∩g(nj))也是候选概念。
步骤4根据规则2 扩展候选概念。
扩展后的候选概念集合如下:
规则2对候选概念集合进行扩展,但其中可能产生新的冗余候选概念,所以在扩展后需要利用规则3再次进行处理。
规则3对于ni,nj∈N,i≠j,若f(ni)⊆f(nj)且g(ni)⊆g(nj)记为ni⊆nj,称ni是冗余候选概念,将其从N 中删除。
步骤5根据规则3 删除冗余候选概念。
步骤4 中的候选概念中,n8,n9,n10,n11⊆n1,n2⊆n5,根据规则3,删除n2,n8,n9,n10和n11,得到的概念如下:
步骤6增加最大概念(O∶f(O)和最小概念(g(A)∶A)。
表1 中,O={1,2,3,4,5},f(O)={b},步骤5 中已存在对应的最大概念,所以不用加入。又因为A={a,b,c,d},g (A)=φ,步骤5 中的概念集合不包含(φ,{a,b,c,d}),将其加入概念集合,最终结果如下:
3 实验结果与分析
为评估算法(GSTCG)的时间性能,将其和经典算法NextClosure 算法进行对比仿真实验。实验软硬件:Intel Core i7-8650U CPU,16 GB RAM,Windows 10 操作系统。算法采用Python3 实现。两个算法在所有背景上都分别运行15 次,实验结果取15 次运行时间的平均值。
3.1 数据集
实验数据集采用人工生成的随机数据集,用3 个参数对数据集进行调节,第一个参数是背景中所包含的对象数|O|,第二个参数是背景中属性集合的长度|A|,第三个参数是属性的填充率f,f∈(0,1)。这里规定每个对象实际拥有的属性数量相同,即每个对象有|A|×f 个属性。
实验数据集有两组,第一组(Bg1)的参数设置为|O|=100~600,每次增加100 个对象,|A|=60,f=0.15,Bg1 中共包含6 个背景。第二组(Bg2)的参数设置为|O|=50,|A|=200,f=0.05~0.3,f 的值每次增加0.05,Bg2 中也包含6 个背景。
3.2 实验仿真
GSTCG 算法和NextClosure(简称NC)算法在数据集Bg1 和Bg2 上的实验结果如表2、图3 和图4 所示。其中表2 是两个算法在12 个形式背景上生成的概念数量情况,结果显示两个算法生成的概念数量一致,证明GSTCG 算法的正确性。
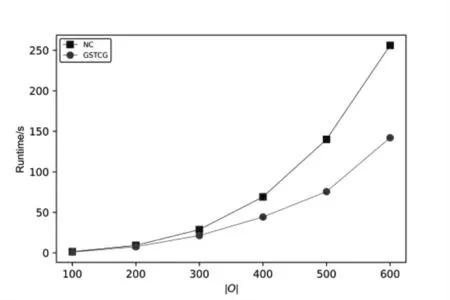
图3 背景1 上的实验结果Fig.3 Results on context 1
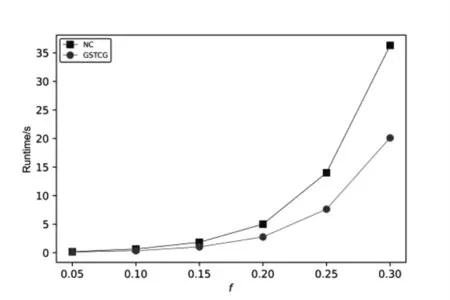
图4 在背景2 上的实验结果Fig.4 Results on context 2
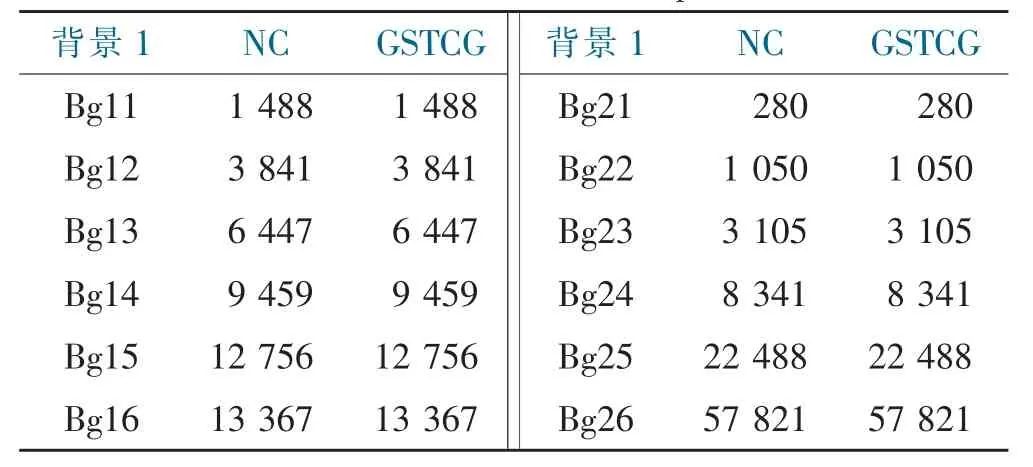
表2 概念数量Tab.2 Number of concepts
图3 是两个算法在Bg1 的6 个背景上的运行时间,图4 是两个算法在Bg2 的6 个背景上的运行时间。
图3 和图4 的结果显示,GSTCG 算法在所有12个背景上的运行时间都少于NextClosure 算法。在Bg1和Bg2 数据集上,GSTCG 算法的平均运行时间分别比NextClosure 算法减少33%和43%。
分析其原因,NextClosure 算法需要逐个生成正规闭包,在查找下一个正规闭包的过程中,重复计算大量无效的闭包,这导致NextClosure 算法运行效率较差。GSTCG 算法中,构建后缀树的时间复杂度是线性的,算法主要的时间开支是步骤4 中的慨念扩展。所以,GSTCG 算法具有比NextClousure 算法更好的时间性能。
4 结语
提出一种新的概念生成算法,其利用广义后缀树生成候选概念,对候选概念进行扩展后删除冗余概念,最终得到形式背景的全部概念。实验结果表明,所提算法能正确生成全部概念,且比经典的NextClosure 算法具有更好的时间性能。下一步的研究中,我们将对广义后缀树生成的候选概念间的关系和候选概念扩展方法进行深入分析,以期更好地提高算法的效率。

