核心素养背景下高中数学教学情境设计的策略

张桂腾

(莆田第十中学,福建 莆田 351100)

深入研究高中数学知识内容不难发现,其部分内容较为抽象,对于学生思维能力要求较高,这时单单依靠教师言传身教显然已难以满足高中生多元化知识能力发展要求.同时核心素养要求学生具备良好的数学知识和实践应用能力,能够灵活地根据实际问题情境进行知识应用,不只是片面地发展个人的理论能力.情境教学法能够构建多样化教学情境,转抽象为直观,化理论为实践,并为师生互动交流创设一个良好的环境氛围,满足高中生多样化的知识能力发展诉求,由此可见情境教学法在教学中的应用对于高中数学实践核心素养有着一定的必要性.

1 高中数学教学情境设计培养学生核心素养的重要意义

1.1 有利于学生知识情境应用能力发展

情境教学法能够强化高中生数学知识情境应用能力.相较于传统课堂教学模式,情境教学法往往会针对不同问题构建对应教学情境,诸如生活化情境、探究性问题情境等等,这些情境无形中为高中生走进特定知识情境创设了一个有利条件,学生得以结合不同情境进行数学知识的应用,并逐步培养知识应用联系问题情境的意识,带动高中生数学知识情境应用能力的发展[1].此外,不同教学情境更容易帮助学生留下深刻的记忆,而当学生再次进行该数学知识的应用时,第一时间想到的便是对应的问题情境,并利用该情境所积累的数学解题经验进行问题的处理,由此看来,情境化教学能够培养学生的情境应用能力.

1.2 有助于拉近数学学习与实际生活联系

基于核心素养下高中数学开展的情境教学模式能够拉近与实际生活的距离.高中数学教学设计应用的情境大都源自于实际生活,或者利用一些生活中的实物来进行教学情境的构建,通过运用高中生所熟悉的生活场景以及一些物品来拉近其与教学情境的距离.这样就实现了数学教学联系实际生活,满足核心素养对于高中生数学知识实际应用能力发展的要求.

1.3 有利于推动数学教学模式创新发展

情境教学法的应用还能够创新课堂教学模式.教学手段会由传统单一的言传身教转变为现代教育技术、实际生活场景以及学生自主探索等多样化课堂教学模式,进而实现教学内容、教学手段以及教学理念等不同维度的创新发展,突破传统课堂教学模式的局限单一,充分发挥情境教学优势,以此来满足高中生抽象思维、实践思维以及数据分析等核心素养的发展诉求,弥补高中传统教学模式所存在的缺陷,最终达到全方位发展学生核心素养目的.

2 高中数学教学融合核心素养开展情境设计策略

2.1 构建实物模型教学情境,促成学生抽象思维能力

立体几何、数轴等数学知识内容较为抽象,学生往往需要借助实物模型辅助他们进行联想和思考,减轻学生掌握这方面抽象知识内容的压力,发展学生抽象思维能力.以“简单几何体的表面积与体积”一课为例,教师在完成基本公式的讲解教学之后,就可以着手实物模型教学情境的构建,例如:一个棱长为b,各个侧面都是等边三角形的四面体S-ABC,请问它的表面积应当如何计算?

学生单单依靠想象以及所给出的图形,很难思考得到求算表面积的具体方法,这时教师就可以进行对应实物模型的投放,让学生近距离观察“四面体S-ABC”的实物模型,发现四面体各个面都是相等的等边三角形,求算其的表面积只需要求出一个面,然后再求算该表面积的四倍即可,这样便可得到四面体S-ABC的表面积,那么解题步骤如下:

过点S作直线SD垂直于直线BC,并交BC于点D.

由题目可知BC=SC=2DC=b

以此来实现实物模型教学情境的构建,让学生学会利用实物模型辅助他们进行抽象知识问题的理解,更加透彻地理解“简单几何体的表面积与体积”的知识概念,实现抽象思维能力的培养.

2.2 联系生活场景搭建情境,培养学生实践思维能力

针对数学核心素养对高中生实践思维能力发展的诉求,往往需要教师密切数学知识学习与实际生活场景联系,为学生创造更多的机会进行数学知识的应用,积累知识应用于实际生活的经验[2].以“随机事件与概率”一课教学为例,教师便可着手生活化教学情境的构建,让学生在生活化情境中尝试知识的实践应用,如下情景:某班同学开展活动游戏,从笔盒五支彩笔中随机抽取任意两支,这五支彩笔分别为红色、黄色、绿色、紫色以及蓝色,外形并无差异,那么请问抽出彩笔有红色的概率是多少?

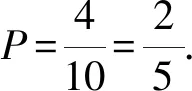
这样学生就能够通过联系他们日常游戏活动情境实现古典概型知识的运用,掌握具体计算方法,实现个人数学实践思维能力的强化.

2.3 创设探究性问题情境,发展学生逻辑推理能力

为弥补高中生知识学习自主性缺失的不足,就需要教师重视探究性问题情境的创设,要求学生围绕教师所投放的问题以及对应问题情境,与同学开展合作交流学习,自主深入探究不同数学问题情境的数学本质内涵,运用自身知识储备解决未知问题,依靠已有条件分析未知因素,最终在思考探索中找到所想要的答案.以“直线与圆、圆与圆的位置”为例,教师可要求学生运用几何法解释圆与圆位置关系,教师提出探究性问题:同学们,已知两个圆分别为O1,O2,其对应的半径分别为r1,r2(r1≠r2),那么这两者的关系分别存在什么位置关系?

学生便会围绕教师所提出的探究性问题情境进行思考,得出以下几种情况:

若圆心O1与O2距离大于r1+r2

那么这两个圆相离;

若圆心O1与O2距离等于r1+r2

那么这两个圆外切;

若圆心O1与O2距离大于|r1-r2|且小于r1+r2

那么这两个圆相交;

若圆心O1与O2距离等于|r1-r2|

那么这两个圆为内切;

若圆心O1与O2距离小于|r1-r2|

那么这两个圆为内含.

这样学生便通过教师所提出的条件以及所构建的探究性问题情境,与小伙伴协作交流推理出两个圆可能存在的位置关系,熟练了几何法应用于圆的位置关系推理,最终达到探究性问题情境提升学生的逻辑推理能力目的,彰显情境教学法对于学生逻辑能力发展效能.

2.4 搭建师生互动教学情境,提升学生数据分析能力

必要的师生互动能够引导学生深度学习,更加精准地掌握知识学习的核心要素,侧重强化个人的核心素养,这也是教师创设教学情境的切入点之一.对此,教师可设置一些互动研究问题,与学生围绕其所设置的互动问题开展交流,潜移默化地灌输知识,引导学生进行数学数据分析,理解不同数据内容的内涵,掌握这些数据在题中的意义,并能够合理利用数据进行问题处理,而教师也达到互动情境引导学生知识学习,辅助学生完成了个人数据分析能力的发展.以“直线的方程”一课教学为例,为发展学生的数据分析能力,教师可进行师生互动问题情境的构建如下:

教师课前提出问题:一条直线需要什么要素才能确定?斜率与直线所对应的关系是什么呢?

学生:两个确定的点可以确定一条直线,一个确定的点和斜率可以确定一条直线,并且每一条直线都有其对应的斜率k.

教师:每条直线并非都有对应的斜率k.

同学:老师,我明白了,当直线倾斜角为90°时,直线不存在斜率k,只有倾斜角不等于90°,直线才有唯一的斜率k.

教师:那么当我们已知直线的斜率k以及直线l所经过的一点P(a,b),应该怎么样求出直线l方程具体表达式呢?

学生陷入沉思,翻找课本寻找答案……

教师:同学们,我们不妨设直线l上的另外一点为P1(x,y),那么就可以尝试运用斜率求算公式进行计算.

学生恍然大悟,运用斜率就算公式得出直线l对应方程式,而教师也通过师生互动情境的构建在师生互动中逐步引导学生理清直线与斜率的关系,实现数据分析能力的发展.

总的来说,情境教学法的应用符合高中数学强化核心素养培养效能的思想理念,亦能够进一步深化其课堂教学改革,为高中生个人核心素养的发展提供更加多样化的教学情境选择,实现知识视野的课外延伸.对此,高中数学教师需围绕本班学生核心素养发展概况,灵活利用多媒体技术、虚拟成像技术、实物投影技术等现代教学设施构建特定教学情境,拉近数学教学与生活实际的联系,帮助学生深层次理解抽象知识概念,构建完整的数学知识体系,最终达到充分发展个人数学核心素养目的.