3D IC-TSV技术的散热特性研究

李丹，刘四平，黄立恒，韩玥鸣，武艺宁

（西安西测测试技术股份有限公司，西安 710000）

引言

自摩尔定律[1,2]提出以来，微电子器件尺寸日益缩小，工艺技术不断改进，电子产品性能得到了极大的改善。但是随着一些工艺技术受到各方面的限制，器件尺寸的进一步减小仍然存在许多难题。3D IC作为一种新生的三维集成电路，已被广泛应用于各种领域，它能够有效解决传统的二维集成电路的性能，并且能够通过三维堆叠的形式，极大地降低系统的功率密度，但是也会面临严重的散热问题，这也是三维集成技术的一个挑战。在这种情况下，如何采取有效的措施来管理和控制三维集成电路的温度，以及解决其中的散热难题，已经成为推动三维集成技术进步的重要因素。

近年来，TSV技术已经成为半导体领域的一项重要突破，其优势显著：既推动了摩尔定律的进一步发展，又拥有极低的尺寸成本，同时还大大增强了3D IC系统的散热效率，使其成为当今半导体领域的主流。3D ICTSV设计采用了一项领先的工艺，它采用在芯片与芯片之间、晶圆与晶圆之间制作垂直导通，以达到芯片之间互联的目的。TSV技术的应用，不仅可以使芯片实现三维方向上的极致集成，而且还具备极少的体积，从而极大地加快了芯片的运行速率，同时也极大地降低了芯片功耗，并且还极大地优化了整个系统的散热特性。

在3D IC热管理研究分析中，一维近似热传导解析模型经常用来预算3D IC热特性。在文献[3]，提出了3D IC温度分布的一维解析模型，并通过模型预测了每层芯片的温度变化情况。文献[4-5]进行了三维集成电路的热分析，并提出了一个分析模型，估算了温度。文献[6]提出了一种用于将3D IC中的功率分布转换为另一温度分布的数值模拟方法。由于TSV通常的填充材料为铜，其导热系数较大，可以有效降低芯片温度，因此温度分析模型加入TSV因子是必要的，而文献[3-6]都未考虑TSV对芯片温度的影响。

本文基于3D IC系统集成为研究对象，依据热力学理论，计算所得TSV的最优直径与间距，应用matlab软件进行仿真，所得结果与Icepak热仿真软件的结果进行对比，说明硅通孔有利于芯片的散热。

1 三维芯片热分析

1.1 不考虑TSV的温度解析模型

根据图1，三维芯片的结构可以分解为由n层芯片堆叠而成，其底部连接热沉或基板，各层芯片之间采用粘合层进行粘合，各层芯片由si衬底和绝缘层构成，热量由每层芯片上有源层产生，假设第n层芯片的热耗为Qn。图2为图1对应的一维热传输模型，芯片内部的热量沿着垂直于芯片的方向上进行传输，最后经过热沉散发出去。其中Rhs、Rpk分别表示为热沉、封装的热阻；Rsi_n、Rglue_n、Rins_n分别表示为第n层的硅衬底、粘合层和绝缘层的电阻；Rn表示为第n层芯片的总热阻。

图1 3D IC的结构示意图

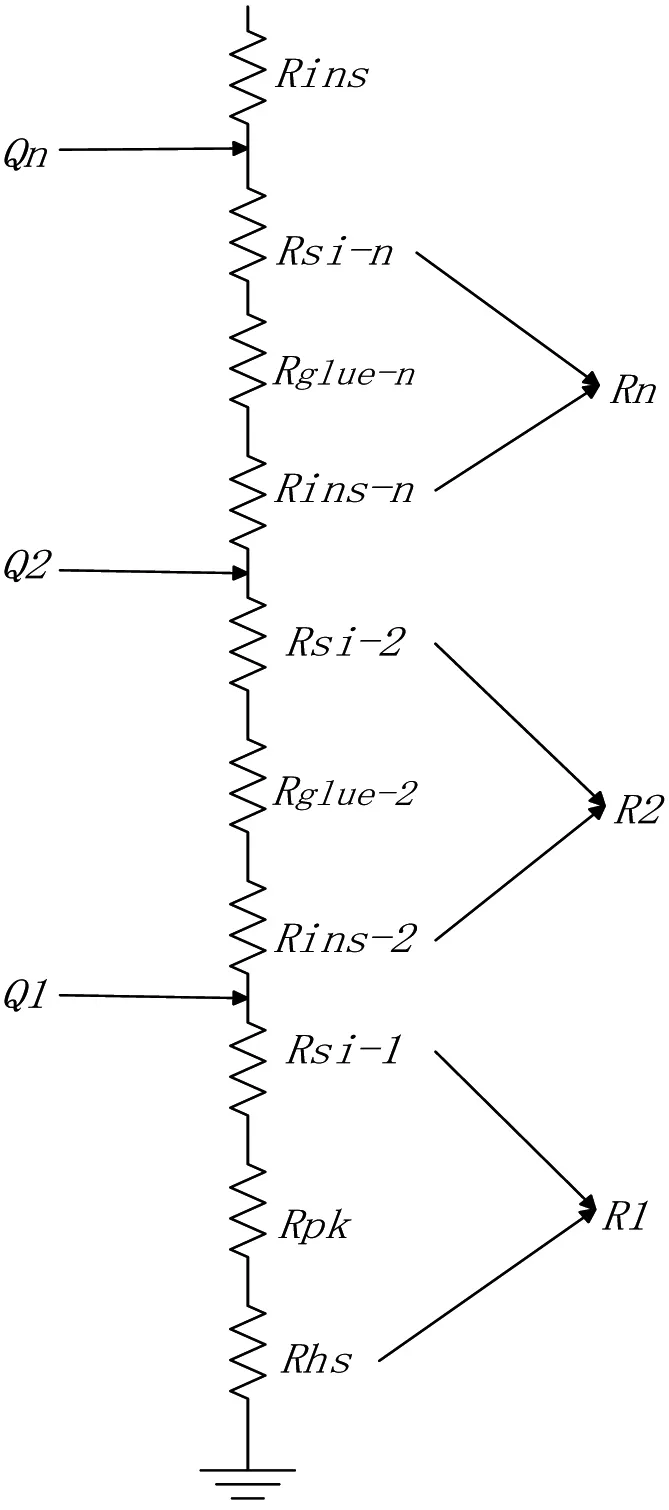
图2 热传输模型

在三维芯片中，由于各层间的粘合层和绝缘层的热导率很低，使得层间的热量传递变得极其缓慢，甚至无法传递下去，每层内部温差相对于各层间的温差可以忽略不计，所以每一层的温度可以定义为每一层的平均温度。三维芯片结构可看成由n层温度不同的二维芯片堆叠而成，依据傅立叶热流分析理论得知，热流可近似为电流I，温度可近似为电压V，热电阻可近似为电阻R。那么第n层温度可表示为：

式中：

Rj—第j层的热阻；

Qm—第m层的功耗；

n—叠层芯片总层数。

假定每层芯片功耗相同，均为Q，第一层芯片热阻为R1，其余层热阻相同，均为R，那么最高层芯片(第n层）温度可表示为：

从图2中可以看出，其余层的热电阻R是si衬底，绝缘层和粘合剂层的总和，第一层热电阻包括si衬底，封装和热沉。由于热阻定义为R=l/KS，l：热流传导的长度，S是热流的横截面积，K是材料的导热系数，Q是芯片功耗 ，n是叠层芯片总层数，所以R和R1可以表示为：

式中：

S—芯片的面积；

Rhs、Rpk—热沉、封装的热阻；

Rsi、Rglue、Rins—si衬底、粘合层、绝缘层的热阻；

lsi、lglue、lins—si衬底、粘合层、绝缘层的厚度；

ksi、kglue、kins—si衬底、粘合层、绝缘层的热传导率。

1.2 考虑TSV后的温度解析模型（适用于matlab)

在三维芯片中，TSV一般填充材料为铜，其热导率大，散热性能强，但是如果忽略考虑TSV，就可能导致芯片温度过高，甚至损坏。因此，在分析三维芯片热特性时，必须充分考虑TSV的影响，以确保芯片的正常运行。

图3为考虑TSV后三维芯片的结构示意图。图4为图3加入TSV后对应的三维芯片的热传输模型，其中RTSV1为第一层通孔的热阻，RTSV为其余各层通孔的热阻。假设每层芯片中通孔的面积总和为STSV，芯片面积总和为S，则可知TSV占芯片面积总和的比例因子为r=STSV/S。

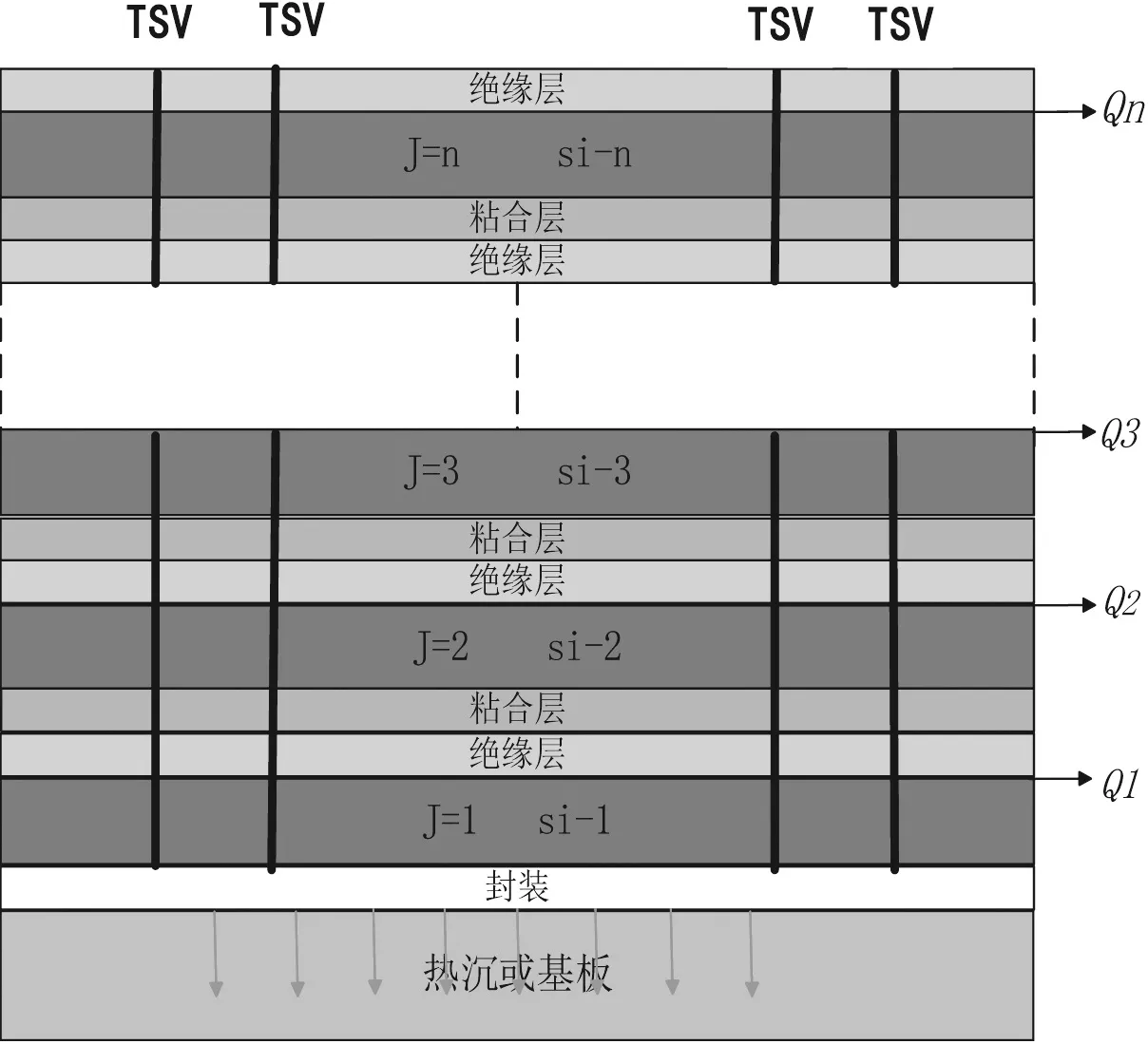
图3 考虑TSV后的3D IC结构示意图

其余各层热阻为：

至此，得到在考虑TSV之后，三维芯片中最高层温度解析模型为：

1.3 考虑TSV后的温度解析模型(适用于ANSYS Icepeak)

由于在 Icepeak建模中，需要输入通孔的直径与数量，所以在1.2节所建立的模型中，通孔占芯片的总面积r已经不适用于该仿真软件。本文需要建立一个关于通孔直径与数量的模型，图5为第i层芯片俯视示意图。其中芯片的面积为10×10 mm2，D为TSV直径，P为两个TSV之间的间距。

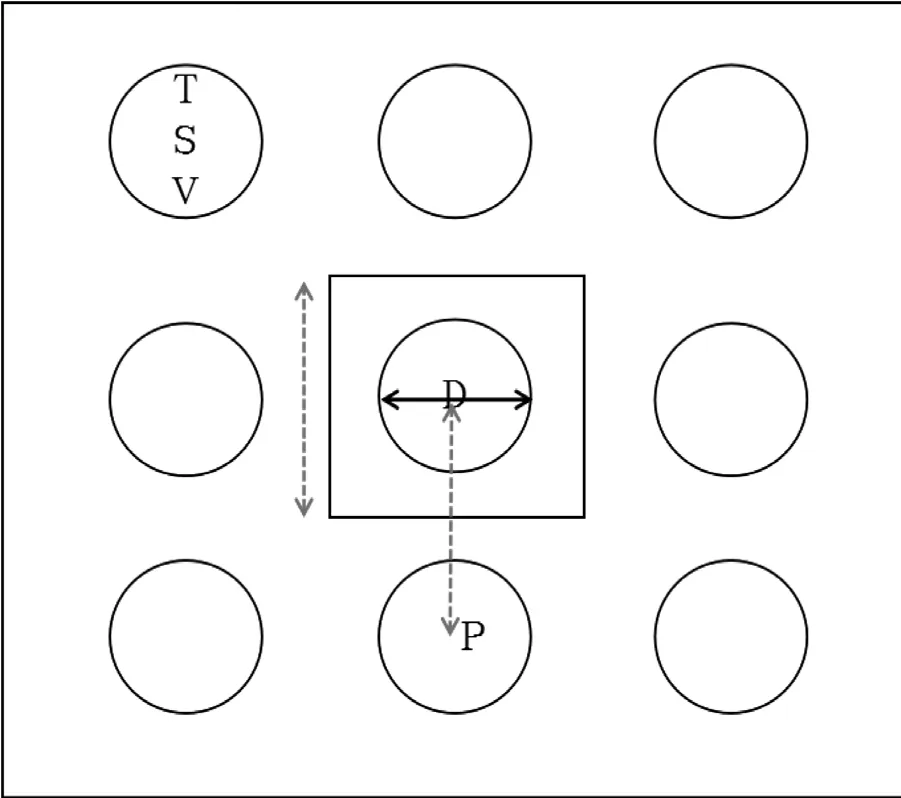
图5 Icepak中的3D IC结构示意图

则根据傅里叶热流分析理论，得到第一层热阻为：

其余各层热阻为：

式中：

P—硅通孔之间的间距；

D—硅通孔的直径，单位为mm；

P2-×D2—除了通孔之外，芯片的其余面积；

3）可以通过搜索引擎，在百度、搜狐上搜索一些熟知的英文新闻网站和英文学习网站，了解最新国内外大事和与四、六级考试相关的资讯。

至此，得到在考虑TSV后，三维芯片中最高层温度解析模型为：

2 matlab进行模型的验证与讨论

在本节中将对建立的3D IC结构模型引用matlab软件进行分析验证，各参数值的典型值见表1。

表1 各参数典型值

2.1 在考虑和不考虑TSV时，最高层芯片温度随芯片层数n变化

通过matlab仿真发现：随着芯片层数n的增加，最高层芯片的温度呈现出明显的上升趋势。当未考虑TSV、n=8时，最高层芯片的温度如图6中黑色曲线所示为150 ℃；当考虑TSV时，图6中的紫色、红色、蓝色三条线对应的通孔占芯片面积的比例因子r值分别为0.000 1、0.001、0.01，可以看出添加通孔时的最高层芯片的温度明显比无通孔时减少了很多。当r=0.000 1、n=8时，最高层芯片温度为147 ℃，比无通孔时降低3 ℃；当r=0.001、n=8时，最高层芯片温度从未考虑通孔时的温度150 ℃降低到136 ℃，降低14 ℃；当r=0.01、n=8时，最高层芯片的温度为126 ℃，比无通孔时降低了24 ℃。这是由于通孔具有散热作用。

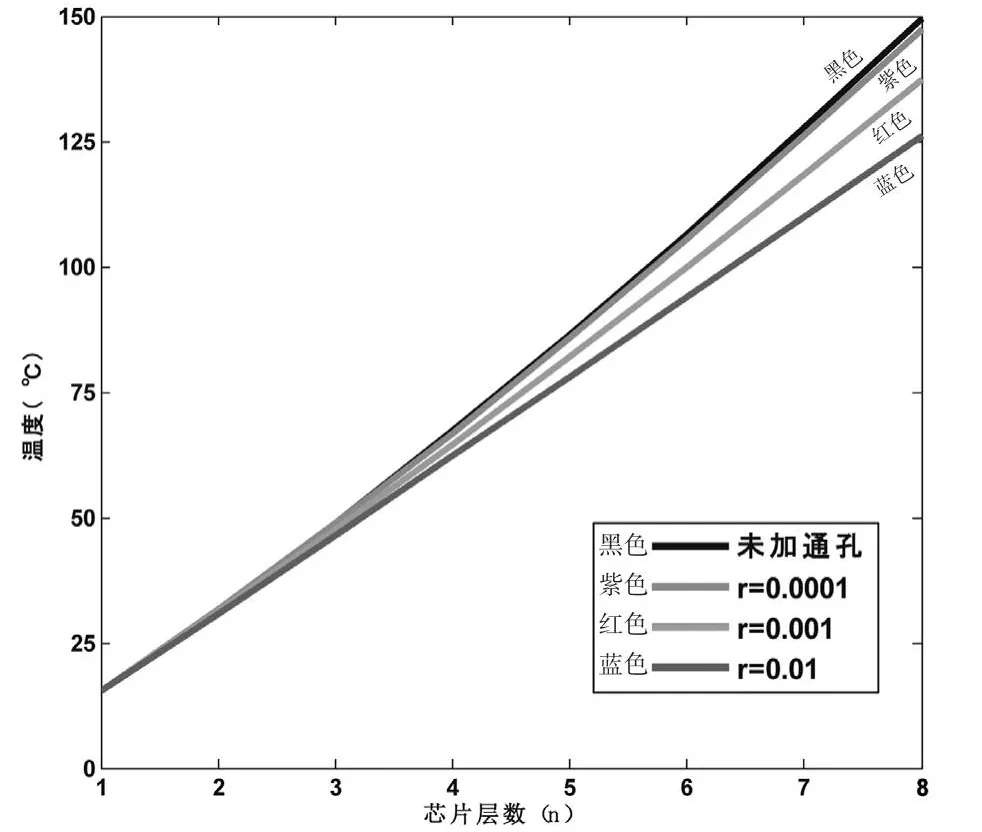
图6 最高层温度随芯片层数n的变化

2.2 讨论芯片层数n=8时，最高层芯片温度随通孔占芯片面积的比例因子r的变化

图7为芯片层数n=8时，最高层芯片温度随通孔占芯片面积的比例因子r的变化曲线。从图7中可以看出，当n=8、r=0.000 1时，最高层芯片温度为150 ℃；当n=8、r=0.005时，最高层芯片温度为128 ℃，比n=8、r=0.000 1时最高层芯片温度下降了22 ℃，下降率为14.7 %；当n=8、r=0.01时，最高层芯片温度为126 ℃，相比n=8、r= 0.005时最高层芯片温度下降了2 ℃，下降率为1.56 %；当n=8、r=0.015时，最高层芯片温度为125 ℃，相比n=8、r= 0.01时最高层芯片温度下降了1 ℃，下降率只有0.79 %，下降幅度很小；随着r的继续增大，最高层芯片温度变化差值十分微小。所以，在进行三维芯片研究设计时，对于芯片层数n =8的情况，最佳通孔占芯片总面积比例因子r的最佳推荐范围在（0.5~1）%之间。

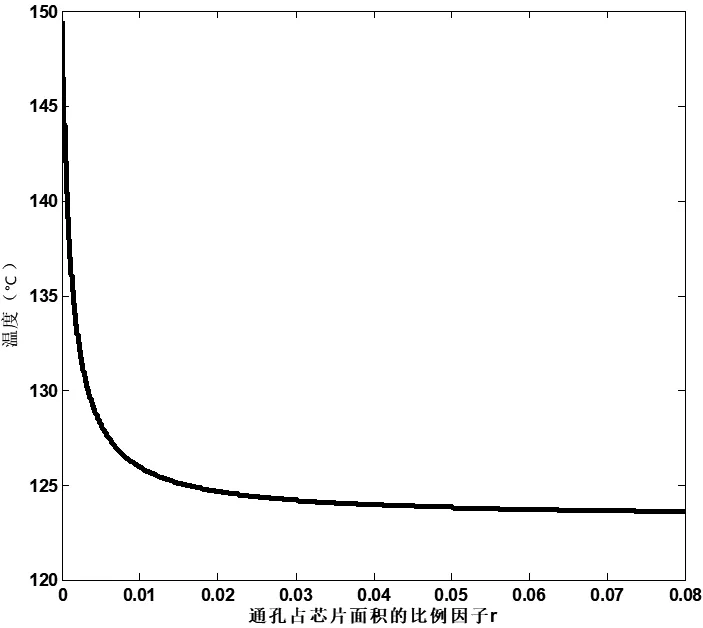
图7 最高层芯片温度随通孔占芯片面积的比例因子r的变化（n=8）

2.3 讨论通孔直径不变的情况下，最高层芯片温度随间距P的变化

图8为当D=0.005 mm、P从（0~0.3）mm变化时，三维芯片中最高层芯片温度随TSV间距P的变化曲线。从图中可以看出，随着TSV间距的增大，最高层芯片的温度不断增加，从123 ℃上升到151 ℃，并无限接近于无TSV时的温度。

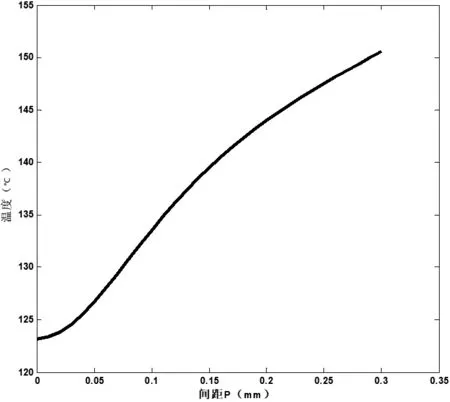
图8 最高层芯片温度随通孔间距P的变化

2.4 讨论通孔间距不变的情况下，最高层芯片温度随通孔直径D的变化

图9为当P=0.2 mm、D从（0~0.02）mm变化时，三维芯片中最高层芯片温度随通孔直径D的变化曲线。从图中可以看出，随着硅通孔直径的减小，最高层芯片的温度不断增大，并无限趋近于无TSV时的温度，这与图6中所得结果相一致。

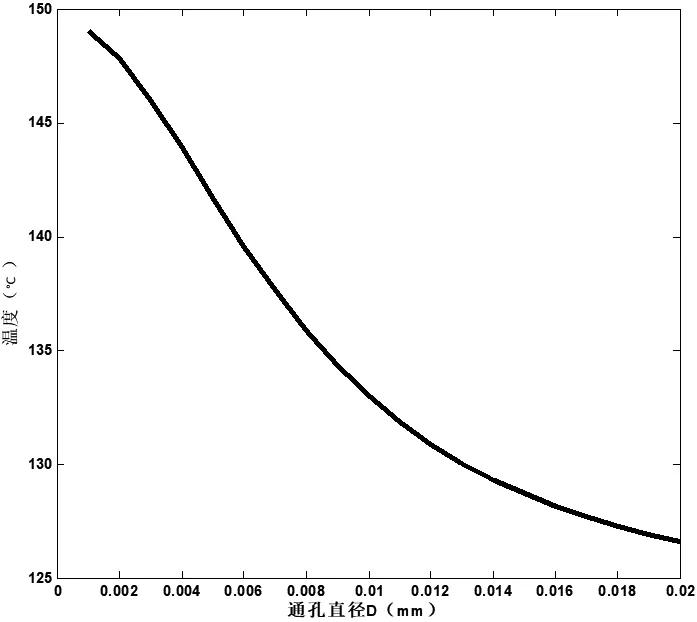
图9 最高层芯片温度随通孔直径D的变化

2.5 讨论9个直径为0.35 mm的通孔时，最高层芯片温度随芯片层数n的变化

如图10所示为9个直径为0.35 mm的通孔（即通孔占用总芯片面积为0.01），最高层芯片温度随芯片层数的变化曲线图。可以看出，当n=8时，最高层芯片温度为127 ℃，其所得结果与图6中r=0.01时的结果相一致。

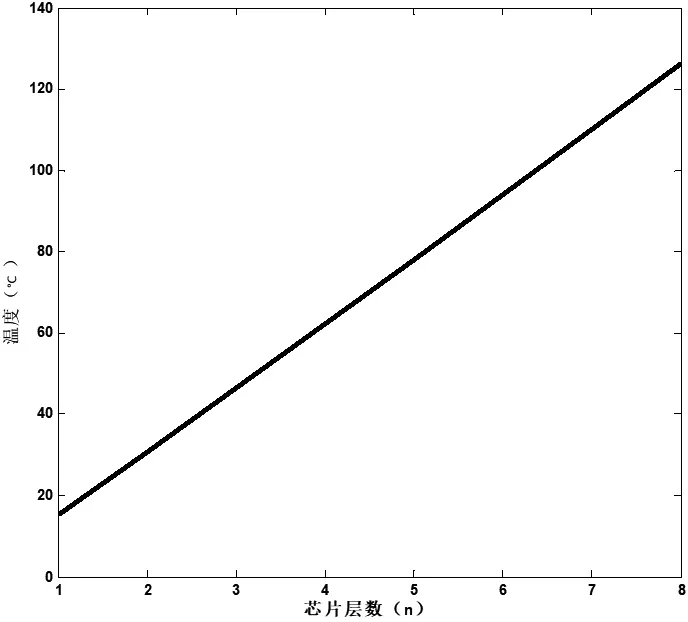
图10 最高层芯片温度随芯片层数n的变化

3 Icepak建模与仿真

为了验证matlab仿真结果的正确性，本文采用Icepak专业热仿真软件，对三维芯片结构进行建模并仿真，所得结果与matlab结果进行对比，并采用适当的散热方式将最高层芯片温度降低到正常的工作范围。

3.1 3D IC模型的设计

本文简化模型尺寸如下，热沉为75 mm×75 mm，芯片的封装尺寸为15 mm×15 mm，裸片的尺寸为10 mm×10 mm，每个芯片的功耗为0.7 W，器件放置在热沉的中心，图11所示为八层芯片堆叠的仿真模型。

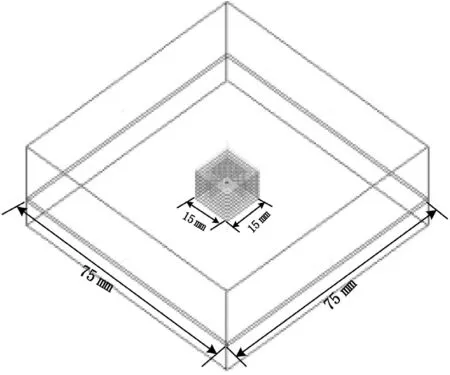
图11 Icepak中的3D IC结构示意图

3.2 仿真及其结果分析

由于在1.3节已给出适用于Icepak的考虑硅通孔的温度解析模型，本节在此基础上进行验证。此简化模型中，八层芯片堆叠，每层芯片面积为10 mm×10 mm，硅通孔数目为9个，通孔直径为0.35 mm，每个芯片功率为0.7 W。该模型求解计算设置为：采用自然冷却散热方式，不考虑流动压力特性和辐射选项，环境温度为20 ℃，得到的未加通孔与考虑通孔后的最高层芯片的温度分别如图12、13所示。

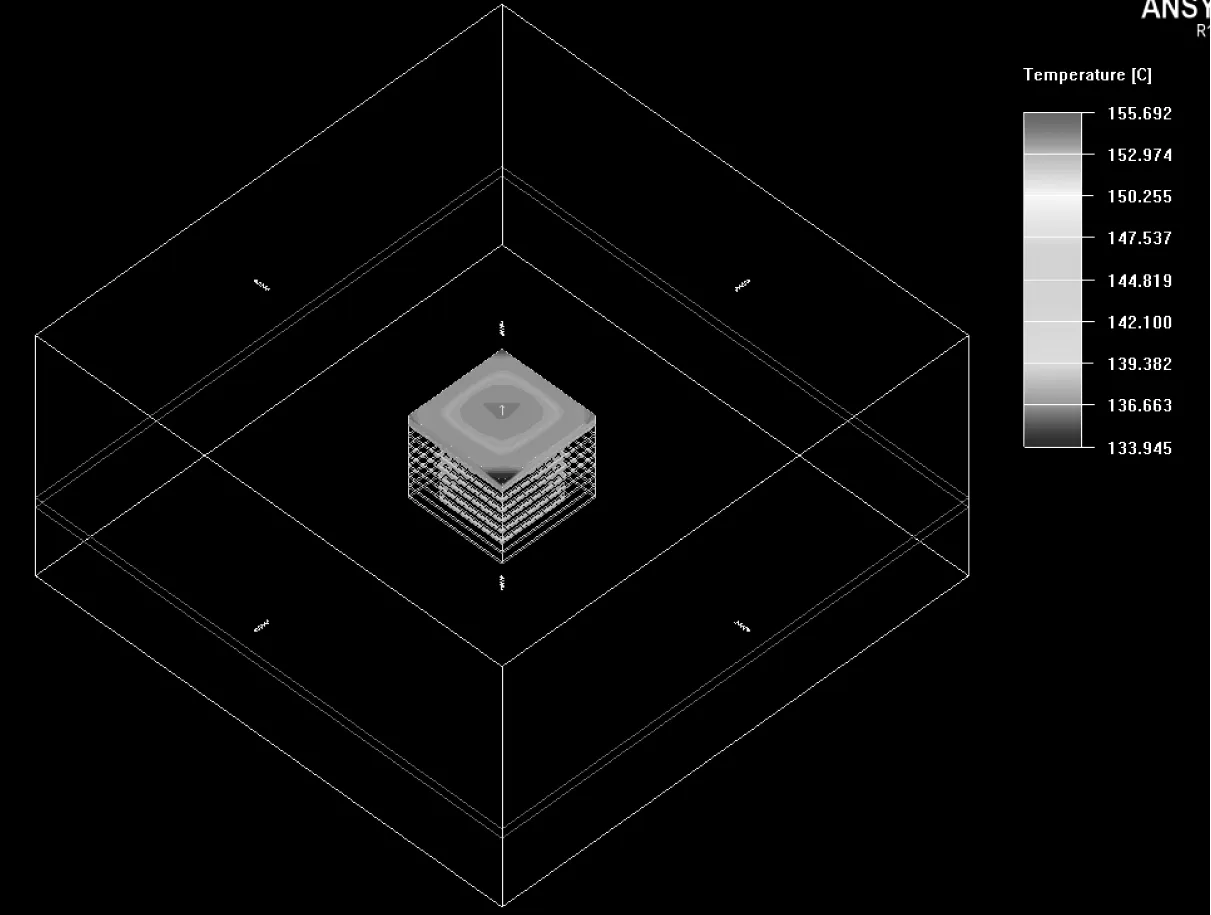
图12 未加通孔时最高层芯片的温度分布图

从图12、图13分别可以看出，当n=8时，未加通孔时最高层芯片的最高温度为155.692 ℃，考虑通孔时最高层芯片的温度为129.879 ℃，此仿真结果与matlab仿真结果150 ℃相差5.692 ℃，127 ℃相差2.879 ℃。由此说明matlab仿真结果与Icepak仿真结果的误差相差甚小，有力地证明了未考虑硅通孔与考虑硅通孔对最高层芯片的温度的影响特性。

4 结论

本文主要研究3D IC—TSV技术，首先提出在无TSV时的n层芯片的温度解析模型，得到其最高层芯片的温度，发现在3D IC中，芯片堆叠层数越高，散热越困难，因而考虑TSV时的n层芯片温度解析模型，基于matlab软件，研究了无硅通孔与有硅通孔（r=0.000 1，r=0.001，r=0.01）时的最高层芯片的温度，从曲线中可以看出：在考虑硅通孔的情况下，且通孔的面积越大时，最高层芯片温度越低，由此说明了TSV有助于芯片散热。相继也讨论了在通孔直径不变的情况下，最高层芯片温度随间距P的增大而增大。在间距P不变的情况下，最高层芯片的温度随通孔直径D的减小而增大。

由于在Icepeak软件中进行分析时，建模需要精确硅通孔的直径大小及数目，所以在考虑TSV的时候需要重新推导公式，考虑通孔直径D和通孔的间距P对于温度的影响因素。基于matlab软件分析发现：在考虑了9个直径为0.35 mm的硅通孔，及r=0.01时的温度解析模型，对于3D IC设计是最佳的工作温度。因此，在Icepeak软件进行建模分析，参数与matlab仿真一致，得到的结果与matlab仿真结果一致，由此说明了考虑硅通孔有助于芯片的散热。