高等数学混合式教学的设计与实践——以离散型第二个重要极限为例

王锋叶，黄元元，李灵晓

（河南科技大学数学与统计学院 河南 洛阳 471000）

高等数学是非数学专业理工科学生的一门必修基础课，它是学生后继专业课的基础，对学生的逻辑思维、演绎思维、归纳思维等数学思维方法的培养以及研究问题能力的提高非常重要。混合式教学是一种将传统教学与网络化教学结合的教学模式，在学习过程中凸显学生的主体性与教师的引导性。第二个重要极限是高等数学中函数、极限和连续这一章非常有用的极限之一[1]，利用它可计算一些特殊未定式的极限，它在实际生活中也有相应的应用，比如银行复利模型、设备折旧问题、元素衰变模型等等。文章以离散型第二个重要极限的讲授为例，结合银行复利模型，给出在高等数学中实施混合式教学的课程设计思路。

1 教学目标和设计思路

教育部印发了《高等学校课程思政建设指导纲要》，要求通过立德树人的根本任务，实现知识传授、能力培养、价值塑造三位一体的教学目标[2]。我们针对第二个重要极限的主要内容制订了如下教学目标：在知识目标上，让学生掌握第二个重要极限的理论推导，知道第二个重要极限的极限结构，会利用第二个重要极限求解一些具有相同结构的数列极限；在能力目标上，通过案例式教学，培养学生应用数学的意识，提高学生分析和解决实际问题的知识迁移能力；在思政目标上，结合数学文化中数学家的事例和教学中的案例，引导学生树立正确的世界观、人生观、价值观。

根据《教育部关于一流本科课程建设的实施意见》，课程设计要求具有高阶性、创新性和挑战度[3]。针对具体教学内容，教学设计思路为：采用混合式教学方式，通过课前、课中和课后的多元教学活动，调动师生、生生互动，实现学生为学习的主体；在教学方法上，采用案例式和启发式教学，融合信息化技术，从易到难，从直观到理论，启发学生进行探究式学习；在案例选择上，采用与学生生活息息相关的实际问题，激发学生学习的欲望，通过解决问题增强学生的成就感；在内容设计上，从简单到复杂，实现教学的高阶性和挑战度，通过课后环节实现课堂内容的创新性迁移。教学设计思路大致概况见图1。

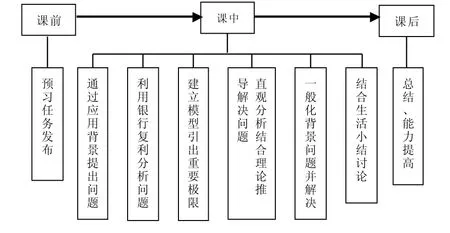
图1 教学设计思路图

2 教学过程

2.1 课前

根据教学目标和教学内容设计课前任务单，目标是让学生具备学习新知识的理论基础，对新知识有大致了解，明确重难点，让学生做到有的放矢。课前任务单为：复习单调有界准则，预习第二个重要极限，观看证明其极限存在的视频；查找资料，了解何为银行单利和复利；结合数学史，谈谈对数学家欧拉的认识。为了让学生对新知识有初步的了解，课前指出课程的重难点：重点是第二个重要极限及其应用，难点是第二个重要极限的应用。

教师通过主题讨论的教学活动检查学生的预习情况。利用学习通后台的学情统计，实时有效地掌握学生课前任务单的完成情况，并通过平台督促提醒学生按时完成课前任务。

2.2 课中

2.2.1 问题引入

首先，教师结合课前关于银行复利的主题讨论，让学生展示个性化学习结果，调动其学习的自信心。提出问题：何为银行复利？银行复利如何计算？教师通过随机选人，让学生总结出复利是一种计息方式，就是把利息计入本金中重复计息，即“钱生钱”“利滚利”。学生具备了理论基础，给出生活实例中的一个简单贷款问题，具体问题为：向借贷公司借了1 万元，年利率是100%，1 年后要还的本息和是多少？抛出问题，让学生觉得所学知识是有用且是有趣，激发其学习欲望。

2.2.2 分析问题，建立模型

利用复利分析以下问题，如借贷公司1 年后结息，1 年后要还的本息和是多少？如借贷公司一年结2 次息，1 年后要还的本息和是多少？如果借贷公司1 年结3 次息，1年后要还的本息和又是多少？如果1 年结4 次、5 次，甚至n 次息，要还的本息和是多少？

教师通过随机选人、学生抢答等方式，让学生从简单到一般、循序渐进地接受以下两点：实例中本息和的表示形式，复利产生的真实效应。比如，如果借贷公司1 年结两次息，1 年后的本息和公式是什么？其中前半年的利息是多少？后半年的利息是多少？让学生能总结出，随着结息次数增多，要还的本息和增多。让学生发问，如果结息次数无限增多，本息和是否也无限增多？

最后，教师引导学生将问题转化，讨论n 趋于无穷大时，数列{xn}的极限是否存在，其中xn=(1+1/n)n，引出第二个重要极限。

2.2.3 解决问题

首先，借助可视化软件呈现随着n 的增大，本息和的数值变化情况。让学生从直观观察到理论推导的过程，引导学生开展探究式学习。通过学生抢答或随机选人等教学活动让学生总结出，数列{xn}是单调递增的，且增长速度前快后慢。分析出实例中要还的钱不会无限增大。

然后，利用可视化软件呈现动点的变化趋势，通过抢答或随机选人的教学方式，引导学生总结出，动点在向一个常数无限逼近，且动点都在直线y=3 的下方，说明数列{xn}有上界，从而分析出实例中要还的钱永远不会超过3万元。引导学生利用复习的单调有界准则，分析并得出数列{xn}的极限存在，从而提高学生的逻辑推理能力。

当学生以为问题已经解决时，教师及时提出，观察不能代替证明，要具有说服力，必须证明。让学生在解决问题的过程中感受数学的抽象性、严谨性和应用的广泛性。

2.2.4 核心知识讲解

首先，结合预习单中视频的观看，通过分组讨论的教学活动完成数列{xn}极限存在的证明。具体讨论的主题是，总结预习单视频中数列{xn}极限存在的证明过程，其中单调性的证明你还有其他方法吗？目的是让学生能理解极限存在性的证明思路。

由于学生的基础知识在目前只能解决第二个重要极限是存在的，还解决不了其极限值就是无理数e，所以，教师结合数学家欧拉的研究介绍该极限值，并将欧拉孜孜不倦、勤奋探索的科学精神融入课程教学，激发学生的学习动力，帮助学生树立正确的人生观和价值观。

然后，分析第二重要极限的极限结构。教师通过课堂抢答或随机选人的教学活动，引导学生分析出第二个重要极限是一个什么形式的未定式？在底上出现的无穷小1/n与指数的无穷大n 形式上有什么联系？通过观察，让学生总结出第二个重要极限是1∞型的未定式，无穷小1/n 与无穷大n 互为倒数。

进一步，教师引导学生思考，当n趋于无穷大时，如果a也是无穷大，那么，数列(1+1/a)a的极限是多少？教师通过变量代换推导出与数列{xn}的极限相等，也等于无理数e。

最后，教师详细解释应用第二个重要极限如何求1∞型的数列极限，并通过随堂练习提高学生对第二个重要极限的应用能力。

2.2.5 学以致用

应用第二个重要极限解决一般贷款问题。教师将引例由易到难，启发学生分析复杂问题。

基于引例中1 年后要还的本息和不会无限增多，教师让学生结合实际思考，是否可以任意贷款，不管贷多少钱，多少年。通过以下问题引导学生进行启发式探讨，如果贷款额为A0元，年利率为r，1 年结n 次息，1 年后要还的本息和是多少？如果其他条件不变，问k年后要还的本息和是多少？如果每时每刻都结息，问k年后要还的本息和是多少？最终问题转化为求趋于无穷大时，数列A0(1+r/n)nk的极限，通过变量代换a=n/r，利用第二个重要极限可知结果为A0erk。

教师总结分析：①k年后连续复利的本息和与n无关，这就说明本息和不会随着计息次数的增多而无限增大，但是它和贷款额、利率和时间都是有关系的。

②当贷款额和利率不变时，利用可视化软件呈现本息和随着时间k 的变化趋势。引导学生观察发现，本息和刚开始增长缓慢，但后面本息和呈爆炸式指数级增长。这就是“利滚利”生成的复利效应，这个模型就是指数增长模型。该模型还可用于细菌繁殖、人口增长等实际问题。

③通过模型分析可知，切勿随意贷款。切入课程思政，提醒学生远离网络贷和校园贷。短期贷款好像还的钱不多，但长期积累特别是还不了利息后，要还的钱是指数级增长，教育学生警惕贷款背后的可怕陷阱，引导学生树立正确的消费观。

2.2.6 小结和讨论

教师总结课堂教学思路，让学生从宏观上掌握课程脉络，并提示学生短期贷款和长期贷款问题都是银行复利问题，再次强调课程的重、难点。

为培养学生在生活中发现数学、应用数学并感悟数学的能力，教师课下通过主题讨论的教学形式引导学生结合生活实际继续探讨连续复利问题。具体讨论主题为：观察复利公式（1+0.01）365≈37.78，1365=1，（1-0.01）365≈0.00255，从每天进步或退步一点的角度，结合生活与学习，谈谈以上式子对你的启发。

2.3 课后

课堂教学结束后，教师利用学习通平台发布教学活动帮助学生总结与提高。通过主题讨论帮助学生自我总结课堂内容，具体内容为，这节课学到了什么？关于这节课学到的极限都知道些什么？怎么应用这节课学到的极限？

为了巩固课堂效果，教师通过题库进行在线测试，提高学生利用第二个重要极限的解题能力，强化学生的解题技巧。

课后拓展指数增长模型，如果r<0，称之为指数衰减模型，该模型可用于元素衰变、设备折旧等问题。讨论区教师引导学生思考问题：已知一种放射性物质，其每年的连续复合衰变率是100%，求10kg 的该物质经过一年衰变后还剩多少？[4]

3 教学总结

本课程采用混合式的教学模式，通过学习通平台的多元化教学活动，师生充分互动，教师时时有效地掌握学生的学习状态，让学生真正成为学习的主体，从而发挥混合式教学模式在高等数学课程中的优势。教师通过有趣、有用的数学应用案例吸引学生的注意力，引导学生分析问题并解决问题，将数学理论与实际应用相结合，培养了学生知识迁移的建模能力，从而让学生通过课程学习感受到能力与素质提高的成就感。在分析问题中，教师借助可视化软件辅助教学，通过直观图形帮助学生分析问题，将现代信息技术与数学教学深度融合。另外，在教学中，教师引入数学文化，盐融于水式地开展课程思政，激发学生的学习动力，并结合案例提醒学生远离网络贷款，帮助学生树立正确的价值观和消费观，将知识传授与价值引领相统一。