智能配电网的分布式并行电压优化方法
郭红伟
(云南电网有限责任公司西双版纳供电局,云南 景洪 666100)
0 前言
在智能配电网分布中,电网的质量逐渐受到了社会各界的普遍关注与重视。分布式电源,是智能配电网中的相重要组成元素,且已经被广泛应用到配电网络中,在一定程度上降低了发电的成本。基于此,为了从比较全面的角度上掌握智能配电网电压优化的分布式,并计算其最优解,本次研究展开了关分析。通过对智能配电网电压优化模型的分析,本次研究是具有现实价值和意义的。
1 智能配电网电压优化模型的分析
在分析智能电网电压优化模型时,从求解接入配电网分布式电源容量问题,作出如下假设:分布式电源的接入点为PQ 节点,分布式电源简称为DG,因分布式电源存在输出功率不可控制的特点,功出力范围为,[0,PDGmax],其中分布式电源的容量问题,可转化为确定其出力的上限问题。为此,本研究提出,电压优化算法控制变量,是分布式电源输出无功率、有功率,状态变量为线路流经功率和节点变压等。第一个优化目标,对功线损耗最小,将分布式电源接入后,将会对系统潮流分布加以改变,实现对网损的减小[1]。但若分布式电源注入容量高,将会增加网损,具体公式如下:
式中,k代表的是支路,Ui和Uj代表的是支路两端节点i和j的电压幅值;Gij代表的线路导纳实部;Nb代表的是线路数目。设置第2个优化目标:
式中,PDGi代表的是节点i处的分布式电源有功出力,NDG代表的是接入分布式电源数目。采用惩罚因子ω,将多目标转化为单目标优化,目标函数如公式(3):
基于上式,设计潮流方程形成等式约束,如公式(4)和(5):
式中,QDGi代表的是节点i处分布式电源无功出力;Bij和θij代表的是节点i和j处的导纳虚部和相位差,N代表的是节点数目。不等式约束,主要为公式(6)~(10):
第一,分布式电源出力约束公式:
第二,节点的电压约束公式:
第三,支路功率的约束公式:
第四,分布式电源总接入容量的限制公式:
式中,代表的是系统负荷总容量;φs代表的是所有接入分布式电源的集合。
2 智能配电网分布式并行电压优化方法研究
2.1 智能配电网分布区域解耦模型
根据对智能配电网分布并行电压的分析,其优化问题分解协调的思想,主要是电网子区域内,能够实现独立的内层比迭代优化计算[2]。在子区域间,通过对边界信息的互换,实现对外层迭代全局潮流的求取,对交换区域内的信息进行重新计算,此种计算方式突出体现为区域内优化计算。在计算期间,需要重复上述内外迭代过程,直至全局优化达到收敛目的[3-4]。本次研究中,主要以2 个区域急性分析,从2个区域解耦模型角度,分外层迭代求取全局潮流分解的协调思路。如图1 所示为智能配电网分布式并行电压区域解耦模型示意图。
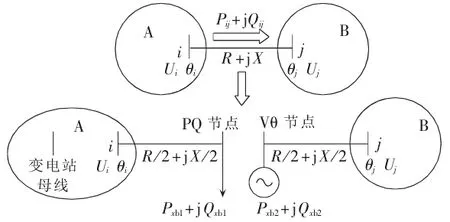
图1 智能配电网分布式并行电压区域解耦模型示意图
根据图中相关信息能够了解到,S 代表配电网,在配电网的2 个子区域A、B 中,通过联络线支路i-j 互联网,在上述联络线支路中点处,逐渐靠近变电站的母线端,引入虚拟性的负荷,另外端引入虚拟发动机。由此,达到断开联络线目的。在此基础上,每个引入的虚拟节点,对应的变量分别为xb1和xb2:
根据上式,能够对边界约束进行表示:
在分析智能配电网分布式并行电压时,在考虑到配电网的辐射性结构基础上,可以主从式问题角度,对全局潮流的分布与并行求解情况加以描述。将主区域设置为靠近变电站的母线区,虚拟的负荷起点[5-6]。设置为虚拟的发电机节点,可为电网提供相对可靠的电压数据;将从区域设置为远离变电站的母线区,虚拟的负荷起点,设置为虚拟的发电机节点,可为虚拟负荷节点,提供相对可靠的功率数据。将主区域和从区域的信息相互交换,反复迭代直至收敛[7-8]。在上述配电系统中,区域A 更靠近变电站母线,将其负荷节点设置为PQ,B 区域更靠近从区域,将其虚拟发电机节点设置为Vθ节点。
2.2 智能配电网电压的序列二次规划算法
本次研究中,对智能配电网电压优化分析时,提出的电压优化算法,主要是从增量形式的角度上,描述控制变量分布式电源出力情况,对系统的不同状态变量所产生的影响。在探讨智能配电网电压的序列二次规划算法时,展开以下假设:DG1∈DGA、DG2∈DGB,分别在节点i和j上,将配电网接入,其出力的变化增量,与在相应i和j节点上的电流源效果具有等同性。由此,能够得出电力网络的线性方程:
在上述方程式中,Y代表的是节点导纳矩阵;ΔUN代表的是节点处电压增量列向量;ΔIN代表的是节点处注入点流量的列向量。非零元素位置上,对应分布式电源的节点位置。由节点电压增量列向量分析,能够得出线路的电流增量列向量,如公式(15):
在上述式中,Yb代表的是线路导纳列向量;A代表的是关联矩阵;对于第k条支路,可从公式角度对其流经功率进行表达,如公式(16):
研究期间,因考虑到节点标幺电压情况,其电压保持在1 <0°左右,因而可得到线路功率增量列向量如公式(17):
对于PQ 型的分布式电源,从恒功率特性角度出发,可明确ΔQDG=MΔPDG,其中,M=diag(tanθ),θ代表的是功率因数角。对于PV 型的分布式电源,考虑其功出力变化情况,无功出力的状态下,在相对约束的范围内作出的调整,会保持节点电压幅度不变,若对节点电压虚部对幅值影响进行忽略,可得以下公式:
式中,R与X,分别代表的是实部与虚部,以系统节点矩阵分布式电源接入的节点相对应。将矩阵M进行定义,M=R-1X,由此得出以下公式:
因而,也就能得出以下表达式:
根据上述公式,明确SP和SQ代表的是线路流经中,有功率和无功率增量,对分布式电源有功出力增量的灵敏度表达矩阵。将目标函数表达式,作为增量形式表现如下公式:
针对第k 条支路,能够对有功线损增量形式进行进一步表示,如公式(22):
通过对该公式的分析,明确Rbk代表的是线路电阻,在功率平方下,线路的增量可表现为如下公式:
从分布式电源角度,并对系统总电源功出力增量公式进行设计,如下:
依据公式(20)~(24)中的相关内容,从目标函数角度,对二次规划问题的标准型公式进行总结,如公式(25)所示:
结合上述公式,对线路功率的极限值约束情况进行综合考虑,将第k条线路,看作时功率约束不等式,将其表现为增量形式:
节点电压、分布式电源最大出力的约束力,也能够从更为简便的角度上,对变量线性不等式进行控制。综合以上,含有分布式电源接入的配电网电压优化模型,可描述为公式(28):
式中,W和b均代表的是不等式约束确定矩阵。
如上文阐述,传统最优潮流问题转换成二次规划的问题,分布式电源是控制变量中的重要功出力,数目低于系统节点数目,且约束条件中,并不存在潮流等式约束,在一定程度上能够保障求解过程的收敛性。依据求解的分布式电源增量结果,对出力情况进行调整,重新规划和计算二次规划问题,再次重复二次规划求解过程[9-10]。上述迭代过程,就是子区域内分布式电源优化处理采用的序列二次规划算法。
2.3 智能配电网电压的分布式序列二次规划算法
本次研究中,为了进一步提高电网电压的优化水平,对分布式序列二次规划算法也展开了探究。内层迭代,是电网电压子区域利用序列二次规划算法,所计算出的分布式电源最优出力[11-12]。外层迭代,是依据内层对分布式电源求解得到的出力情况,实现对边界节点信息的互换和求解。通常情况下,在外层迭代后,电源系统各子区域将根据当前潮流信息情况,对区域有功线损增量情况加以确定,对其他各区域的分布式电源出力增量灵敏度矩阵进行计算,并明确分布式序列二次规划算法,在特定区域内的应用。
3 智能配电网的算例分析与比较研究
3.1 实验建立与自动区分算法的比较
在研究期间,为了进一步验证上文提出的方法可行性,对接入的分布式电源节点系统算例,进行电压优化分析。比借助MATLAB 对程序进行编写,运行环境可为Intel i5-3210N 2.5GHz 处理器。如图2 所示33 节点系统及分区示意图,根据图中相关信息能够了解到,节点15 与节点32 处,分别接入了2 个PQ 型的分布式电源。
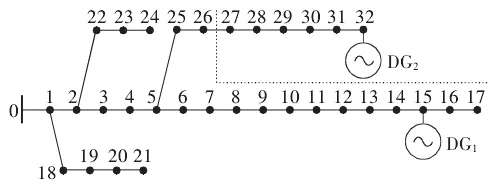
图2 33节点系统及分区示意图
分布式电源中的相关参数,见表1。
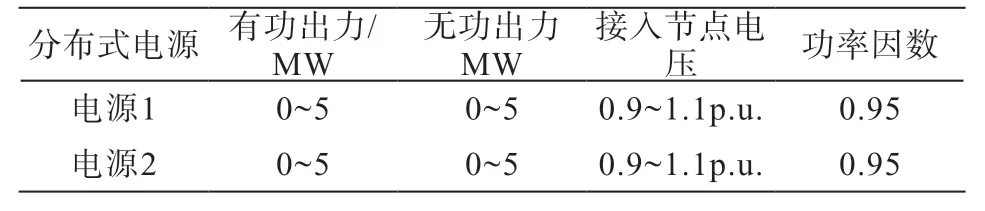
表1 2个PQ型分布式电源的参数情况
目前,常用的聚类算法是模糊聚类FC 算法,借助统计量F,对表征分区的合理程度进行区分。而与凝聚层次聚类法相比,分区数目相同的情况下,凝聚层次聚类法的优势要显著高于模糊聚类FC 算法。因而,凝聚层次聚类法更加适用于分区数目多的情况下。
3.2 智能配电网分布式算法的优化结果

图3 33节点系统电压幅值示意图
3.3 惩罚系数对算法的影响
经过实验分析,得出惩罚系数ω的优化结果如表2 所示,分布式电源出力程度,通常是随着惩罚系数的升高,而呈现出明显增加的趋势,二者为正相关关系。该研究结果,也是目标函数中分布式电源有功出力最大所占权重,逐渐升高将会出现的必然性结果。在分布式电源出力升高的趋势下,系统潮流逆向流动呈现出明显增强的趋势。ω=0,目标函数只考虑有功线损最小,ω≥0.2,接入的分布式的电源处节点电压幅值,将达到上限。
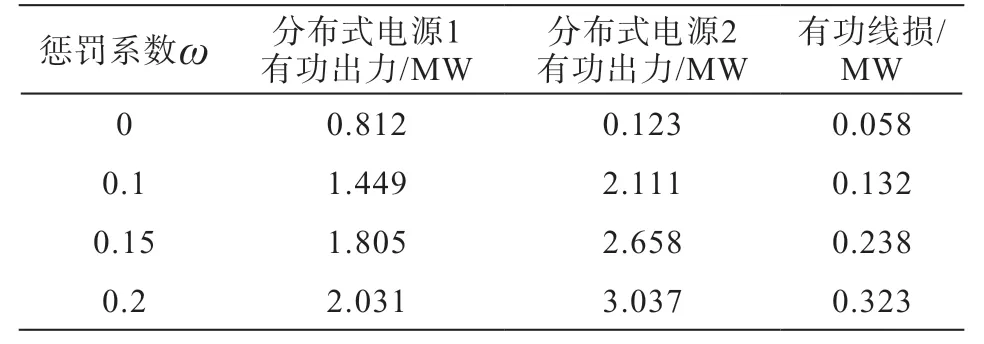
表2 不同惩罚系数下的优化结果分析
3.4 分布式序列二次规划算法与辅助问题原理比较
利用目标函数可分解的优势,可将辅助问题原理引入到目标函数中,用于求解函数最小值。对分布式序列二次规划算法与辅助问题原理算法进行比较。结合上述节点系统区分方案,得出有功线损最小优化目标,具体优化结果如表3所示。与辅助问题原理算法相比较,二次规划算法无论是在有功线损方面,还是在内层迭代收敛次数方面,都存在相对客观的现象,由此说明,在更好的收敛性能角度下,能够获得最优解。辅助问题原理算法在应用中,局部最优解更好。
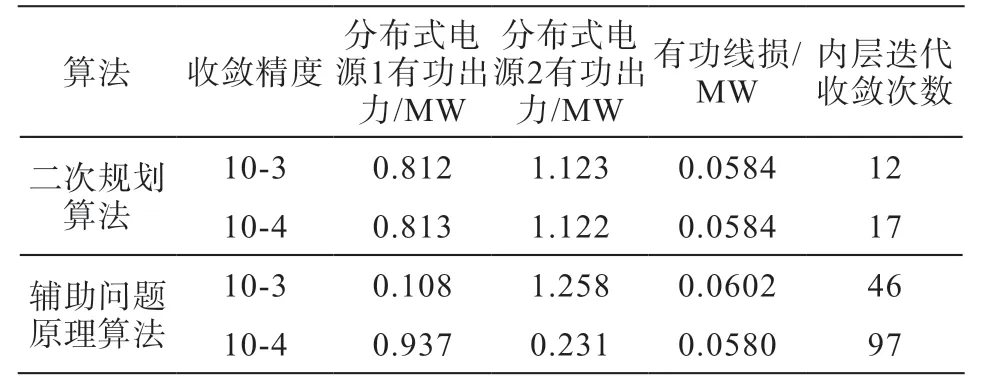
表3 二次规划算法与辅助问题原理算法的优化结果分析
4 结束语
在本次研究中,通过对智能配电网自动分区方案的分析,构建了与之相适应的分解协调模型。同时,采用增量表达式的方式,对智能配电网电压优化模型进行描述,提出了分布式序列二次规划计算方法,将其应用于并行求解分布式电源最优出力中。在前后节点电压变化优化前与优化后的分析、其他并行求解方法优化结果的分析,证实分布式序列二次规划计算方法在提高系统电压治疗方面,具有较为突出的优势。在本次相关内容的研究下,能够为日后提高智能配电网自动区分方案的应用水平,提供宝贵建议。

