微磨料水射流抛光喷嘴数值模拟及磨损规律分析

林 琳, 张云朋, 蒋东岑, 赵志磊, 尤 晖

(1.广西大学 机械工程学院, 广西 南宁 530004;2.广西制造系统与先进制造技术重点实验室, 广西 南宁 530004)

引言

微磨料水射流抛光(Micro-abrasive Water Jet,MAWJP)是一种精密抛光技术,因其切削力低,灵活度高,精度高,无热影响区以及加工范围广等优点,被广泛应用于玻璃,陶瓷,合金以及特殊材料的自由型面和微槽等精密加工[1-2]。喷嘴是磨料水射流的直接执行元件,在加工的过程中,由于微磨粒持续撞击和冲刷喷嘴内表面,造成喷嘴几何结构发生改变,直接影响射流稳定性,进而影响射流抛光加工效率和精度[3]。因此,深入分析MAWJP喷嘴内流场特性, 探讨其磨损机理,减轻磨损延长其使用寿命,提高射流稳定性,是亟待解决的问题。

目前国内外学者关于磨料水射流喷嘴磨损的研究主要分为两个方面[4-8]:一是从工艺参数角度对喷嘴磨损特性进行研究,二是从喷嘴结构和材料方面对喷嘴进行优化。在相关研究中,由于射流工艺的特殊性和复杂性,流体的运动状态以及磨料颗粒运动很难通过实验捕捉,从而导致研究喷嘴磨损机理难以实现,因此在众多研究中采用最多的研究方式是数值模拟。为研究各参数对后混合式磨料水射流喷嘴磨损的影响,QIANG Zhengrong[9]、KAMARUDIN N H[10]等基于欧拉-拉格朗日方法,结合FLUENT中DPM模型对气液固三相内部流场进行建模分析,通过对切割喷嘴内部流动状态和颗粒混合过程进行数值模拟,研究分析了系统参数、磨料特性以及几何结构对喷嘴磨损的影响。管金发等[11-12]学者基于DPM模型,利用Fluent软件和E/CRC磨损模型研究了不同射流参数、磨料参数以及喷嘴结构对前混合磨料水射流喷嘴磨损的影响,研究发现喷嘴壁面磨损呈现双峰特性,特别是在喷嘴圆柱段入口处及靠后部分磨损较为严重。CHEN Xiaochen等[13]基于欧拉-拉格朗日方法研究了磨料颗粒运动,通过分析在不同收缩角和不同长径比情况下,磨料对喷嘴内表面磨损分布,提出了一种双梯度结构喷嘴,研究结果发现,双梯度结构喷嘴能够有效降低喷嘴磨损,但对其结构优化还有待进一步研究。ANAND BALA SELWIN K P等[14]学者为研究喷嘴内壁面磨损情况,提高喷嘴耐磨性和改善加工工艺,以喷嘴的几何形状和喷嘴的材料为参数对仿真结果进行优化,结果表示70°锥度进料角和碳化钨材料喷嘴相对较好。综上可以发现,目前在喷嘴磨损研究中,磨粒的运动大多采用离散相模型(Discrete Phase Model,DPM)进行计算,而该模型适用于低浓度(磨粒体积分数小于10%)场合问题,尽管使用DPM能够较好计算出颗粒运动过程,但是由于该模型无法考虑颗粒间以及颗粒与壁面间的相互作用,计算得到的颗粒运动结果精度低,并且得不到颗粒间的碰撞力以及颗粒与壁面之间的碰撞信息,因此该模型在计算颗粒运动特性中具有一定局限性。为了弥补离散相模型研究的不足之处,充分考虑颗粒间相互作用及颗粒物理特性,离散单元法(Discrete Element Model,DEM)被提出用于分析研究离散颗粒的运动特性,该模型对颗粒浓度没有限制,并且通过接触力学模型能够研究颗粒间以及颗粒与几何体间相互作用,并以此得到颗粒间及颗粒与几何体间接触信息及颗粒运动信息[15]。为研究在流体中的颗粒运动特性,通过将计算流体力学与离散元法 (CFD-DEM)相结合有效的解决了这类问题,该方法目前在农业加工、喷砂以及气力输运等领域得到广泛应用[16-17]。周大鹏等[18]通过利用Fluent-EDEM软件和实验研究分析喷砂喷嘴结构对加工过程的影响,并通过实验验证利用Fluent-EDEM数值计算的准确性。ZHAO Xiangyang等[19]通过CFD-DEM耦合方法跟踪了不同位置释放的颗粒运动轨迹,并分析颗粒在三通管道内对壁面的冲蚀磨损。WANG Yangping等[20]学者通过CFD-DEM方法研究了高浓度二元混合颗粒在离心泵内的流动特性以及对壁面的冲蚀磨损模型。可见CFD-DEM耦合方法为研究流体与颗粒的混合特性及流动特性提供了一种有效研究思路,微磨料水射流抛光作为典型的固液流动问题,磨料在喷嘴内对壁面冲蚀以及在抛光过程中对材料去除起关键作用,而该方法在MAWJP研究中对磨粒运动特性及磨粒冲蚀喷嘴分析鲜有报道。

磨粒频繁撞击冲蚀喷嘴壁面产生微力是造成MAWJP喷嘴磨损的主要原因,目前关于磨粒运动特性研究大多采用的DPM模型将颗粒进行无体积处理,忽略了颗粒间及颗粒与壁面间的相互作用问题,因此无法准确得到颗粒复杂行为信息。为更准确的探讨射流精密抛光喷嘴磨损规律,采用离散元方法考虑颗粒间及颗粒与壁面间相互作用,并基于CFD-DEM耦合方法和Oka磨损模型建立数学计算模型,利用Fluent和EDEM软件对前混合磨料水射流抛光不同结构和不同硬度的喷嘴进行数值模拟,探讨不同喷嘴结构和材料硬度下对喷嘴壁面受力及磨损的影响规律,揭示喷嘴壁面受力与喷嘴磨损的关系,同时分析不同黏度的液体对喷嘴磨损影响规律,为后期喷嘴结构优化设计以及预防喷嘴磨损提供新视角。

1 磨料射流抛光数值模型建立

CFD-DEM是基于欧拉-拉格朗日法相关理论建立的耦合模型,该模型不仅能够对具有各自特性的颗粒和流体进行模拟计算,同时能够通过离散元考虑颗粒的形状,密度等物理特性,并且能充分考虑颗粒和流体间的相互作用及颗粒间的相互作用,能够更真实用于模拟计算工程中的相关问题。

1.1 数学模型

本研究中假设颗粒均为均质软球体,流体为不可压缩且流体与周围环境之间不存在传热。在实际情况下,喷嘴内实际流体是具有一定黏性的,故连续相控制方程如下式[21]:

质量守恒方程为:

(1)

动量守恒方程为:

(2)

(3)

式中,ρl—— 液体密度

ul—— 流速

p—— 压力

τ—— 黏性应力张量

Fp-l—— 颗粒与流体之间的阻力引起的相互作用项

磨料在流体中的复杂运动是由于作用在颗粒上的力较为复杂,通常会受到流动阻力、压力梯度力、浮力、质量力和升力等影响。此外由于磨料粒径小,颗粒间相互作用除了存在碰撞力外,颗粒间的相互作用力也应当考虑,Hertz-Mindlin with JKR模型通常用来考虑颗粒间的相互作用力,根据牛顿第二运动定律,离散相控制方程如下[22]:

(4)

式中,mp—— 磨料的质量

vp—— 颗粒速度

Fc—— 颗粒间及颗粒-壁面间的接触力

Fd—— 流体对颗粒的阻力

FJKR—— 颗粒间相互作用力

接触力FJKR的法向分量取决于法向重叠量和颗粒的表面能量,其表达式为[23]:

(5)

(6)

(7)

(8)

式中,E*—— 等效杨氏模量

E1,E2—— 磨粒的杨氏模量

ν1,ν2—— 磨粒的泊松比,其中E1=E2,ν1=ν2

γ—— 磨粒的表面能

R*—— 等效半径

R1,R2—— 颗粒半径

δ—— 颗粒接触的法向重叠量

a—— 颗粒接触点的接触半径

1.2 磨损模型

在磨料水射流抛光过程中,磨料颗粒受流体加速后冲蚀工件以达到表面去除效果。磨料在喷嘴内获得较高速度,与喷嘴内表面发生冲蚀和频繁碰撞,导致喷嘴磨损加剧,因此需要考虑磨损模型来计算喷嘴磨损。目前常用的磨损模型有Finnie[24]、E/CRC[25]、Oka[26]和Archard[27]等磨损模型,本研究采用EDEM中内置Oka磨损模型,该模型属于冲击磨损模型,其示意图如图1a所示,并以几何表面的磨损深度表示磨损量为:

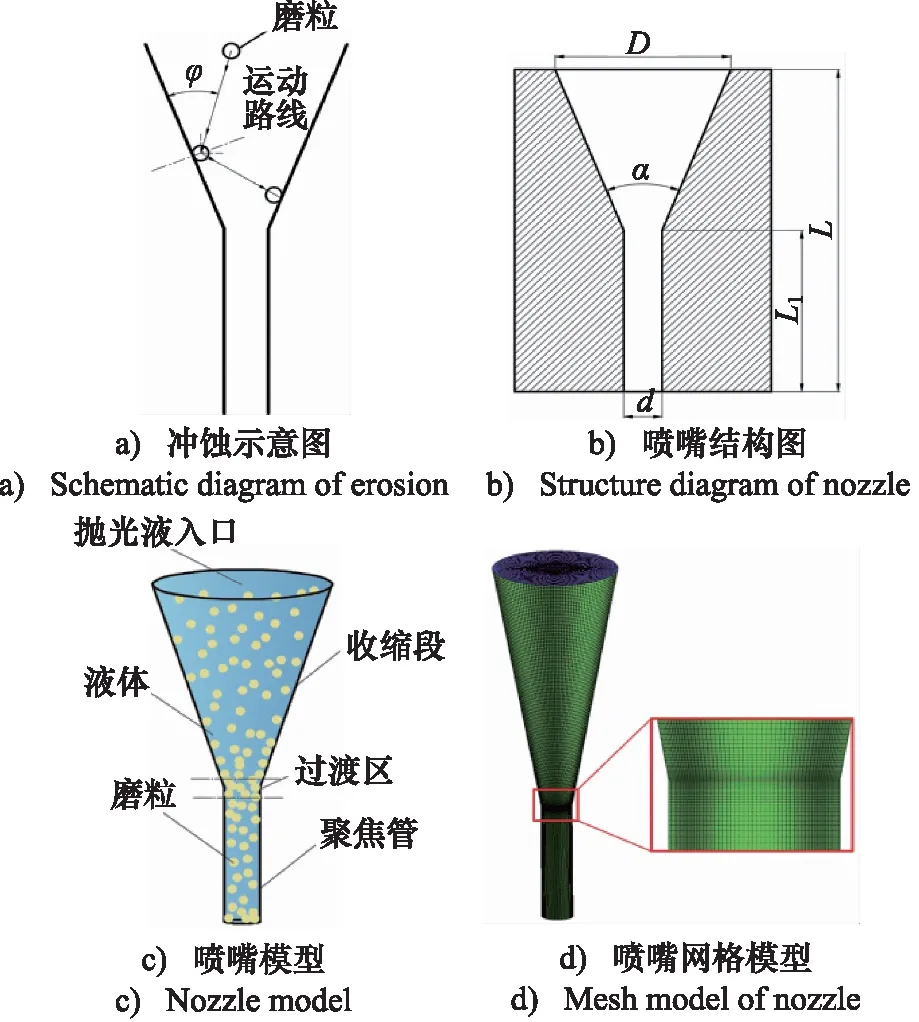
图1 喷嘴结构模型及网格划分Fig.1 Nozzle structure model and grid diagram

(9)

其中,f(φ)依赖于冲击角的归一化冲蚀量,由下式给出:

(10)

E(φ)为单位质量的磨损量,由下式给出:

(11)

式中,DH—— 磨损深度,mm

φ—— 颗粒冲击角

mp—— 磨料的质量

A—— 冲击表面面积,mm2

HV—— 材料的维氏硬度

Woka—— 材料的磨损常数

k1—— 实验得出的常数

2 仿真模型设置及验证

在本研究中,连续相采用Fluent 18.0软件计算,对喷嘴内流体进行瞬态求解,获得相应的流场;离散相采用EDEM2021.2软件计算,并通过外部编写的耦合接口,将获得的流体相关数据导入到EDEM中,根据牛顿第二定律对磨料粒子进行求解,以获得喷嘴内颗粒运动特性以及颗粒与壁面碰撞特性。

2.1 喷嘴内流场仿真模型设置

喷嘴的作用是通过将水压转化为动能冲击工件表面,以此达到抛光效果,不同喷嘴结构会产生不同射流效果。有学者针对不同结构的喷嘴进行研究,结果表明,锥直形喷嘴结构具有较好射流效果[28],因此本研究采用锥直形喷嘴为仿真模型,简化结构如图1b所示,一般喷嘴结构包括收缩段、过渡区(变截面处±0.5 mm)和聚焦管,如图1c所示。固定喷嘴入口半径R为2 mm,出口半径r为0.5 mm,收缩角α和聚焦管长度为L1可变参数。通过改变长径比n(聚焦管长度与喷嘴出口直径的比值)和收缩角可以得到不同参数的喷嘴结构。

在用三维软件建好物理模型后,导入到ICEM CFD对喷嘴进行网格划分,考虑到在收缩角与聚焦管连接处,流体运动相对比较复杂,在该连接处对喷嘴网格进行加密,网格划分如图1d所示。喷嘴网格划分完成后,首先在EDEM软件中设置颗粒及喷嘴模型。在实际加工过程中,喷嘴内不断有颗粒通过,因此在喷嘴入口处设置动态颗粒工厂,颗粒随机产生,颗粒数量不受限制,颗粒相步长一般按Rayleigh时间步长的10%～40%[15],本研究离散相时间步长设置为Rayleigh时间步长的15%。

在Fluent中对喷嘴内流场进行数值模拟时采用双向耦合,在与EDEM耦合过程中,流场信息不断更新变化,在Fluent中设置基于瞬态压力求解器对流场进行模拟计算。湍流模型采用RNGκ-ε模型,采用基于SIMPLE半隐式耦合算法来耦合流场中的速度场和压力场,具体参数设置如表1所示。在软件中设置好模型后,在Fluent自定义模块中加载耦合Fluent和EDEM的接口文件,并在接口文件中设置阻力,升力等耦合细节。建立完成耦合后,在Fluent中设置时间步长,Fluent中时间步长通常是EDEM的时间步长的1～100 倍[15]。

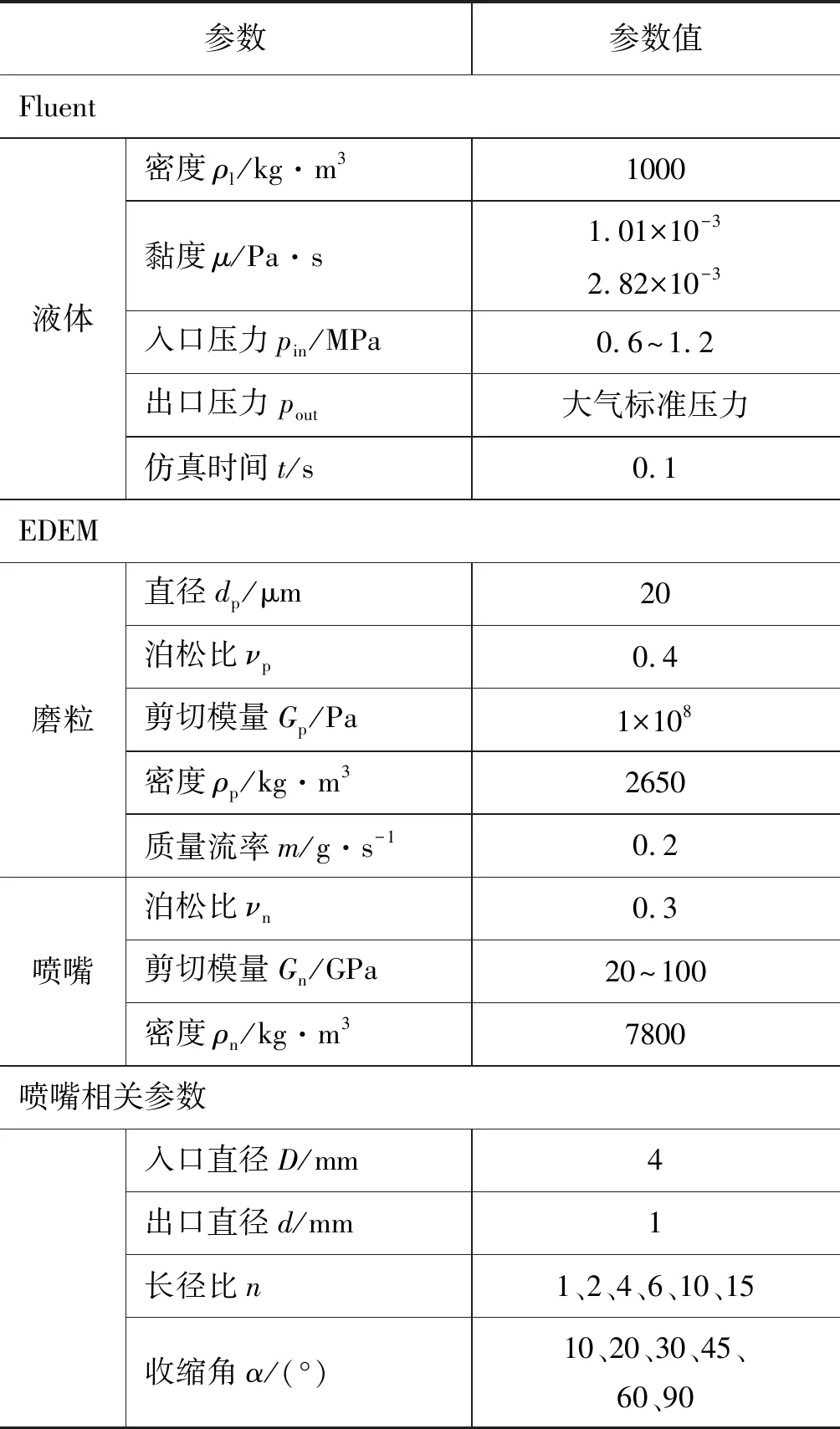
表1 仿真参数设置Tab.1 Simulation parameter settings

2.2 网格无关性分析及模型验证

1) 网格无关性分析

网格质量是影响数值计算精度的主要因素之一,为了验证网格对计算精度的无影响,以相同方式划分三组不同数量的网格,进行网格无关性分析,其网格划分数量如表2所示。

表2 网格数量Tab.2 Grid number

当工作压力pin为0.6 MPa时,不同网格单元数量喷嘴轴线上射流总压的变化如图2所示。从图中可以看出,射流压力沿射流方向y逐渐降低,对比三种网格单元数下,射流压力p变化趋势基本一致,而网格1的射流总压在过渡区略低于网格2与网格3,当网格单元数从600706增加到893544时,射流总压变化曲线几乎重合,因此可知当网格单元数增加到893544时,网格数量对计算精度几乎没有影响,故在保证计算精度以及降低计算成本的情况下,本研究采用网格单元数为600706进行计算。

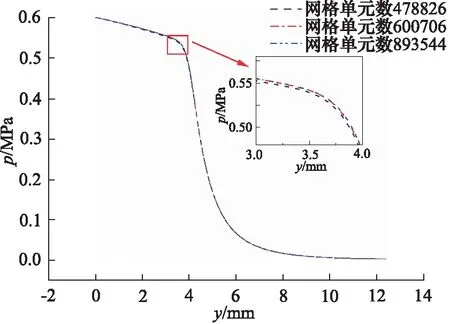
图2 网格无关性分析Fig.2 Grid independence analysis

2) 模型验证

射流速度V是影响磨料射流加工的重要参数之一。为了验证上述仿真模型的准确性,通过实验测量入口压力pin范围为0.4 MPa～1.4 MPa时喷嘴射流流量,并根据流量与流速之间的关系进行计算,通过对比不同压力下的实验值与模拟结果来验证该模型的准确性,其磨料水射流抛光系统如图3所示。

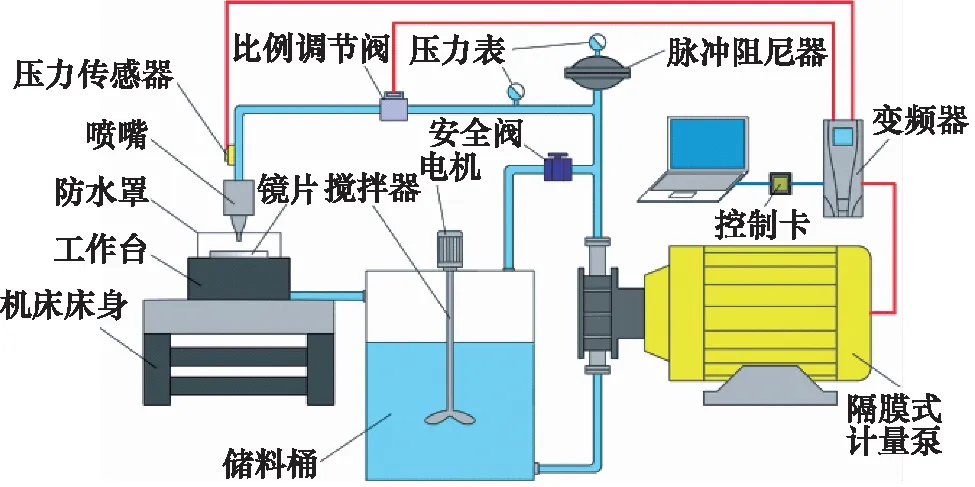
图3 磨料水射流抛光系统Fig.3 Abrasive water jet polishing system

实验在由实验室自行研发设计的机床设备上进行,试验设备图及实验喷嘴如图4所示。

图4 微磨料精密抛光加工平台Fig.4 Micro-abrasive precision polishing machining platform

当系统工作压力pin为0.6 MPa时,数值模拟得到射流速度V为34.6 m/s,实验测得射流速度为36.3 m/s,数值模拟与试验得到的射流速度与压力的关系如图5所示。从图中可以看出数值模拟与试验得到的射流速度存在一定误差,其中两者之间相对误差为4.54%,由此可见数值模拟与试验值相差并不大,基本上符合计算结果,因此上述模型在误差允许范围内具有一定的准确性和有效性。

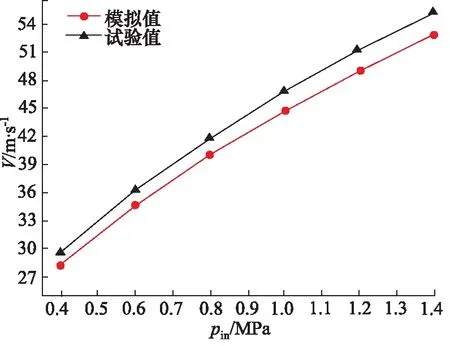
图5 模型验证Fig.5 Model verification

3 模拟结果分析

3.1 喷嘴结构对内表面磨损规律

1) 收缩角对喷嘴磨损的影响

考虑到较小的长径比n会降低射流动能及射流聚集性[29],图6显示了系统压力为1.2 MPa,流体黏度为1.01×10-3Pa/s,喷嘴长径比为4时,不同收缩角对喷嘴磨损影响规律。以喷嘴内表面磨损深度(DH)为磨损量作为参考,其中以喷嘴内表面的最大磨损量进行对比分析。从图6可以看出:喷嘴最大磨损量DH随着喷嘴收缩角α增加而逐渐增大,当收缩角为10°时,壁面受到总碰撞力F约为0.00291 N,磨损深度约为0.0136 μm,而随着收缩角增加,当达到90°时,壁面受到总碰撞力F约为0.00726 N,磨损深度约为0.185 μm。收缩角越大喷嘴磨损越严重,其原因是当喷嘴收缩角较小时,磨粒在喷嘴内轴向动能起主导作用,磨粒与壁面碰撞频率较低,壁面受力较小,而随着喷嘴收缩角增大,磨粒径向速度得到提高,磨料与壁面发生碰撞频率明显升高,颗粒与壁面碰撞后会产生反弹,而在流体带动下导致颗粒与壁面发生二次或多次碰撞,对壁面产生的碰撞力增加,导致喷嘴磨损加重。

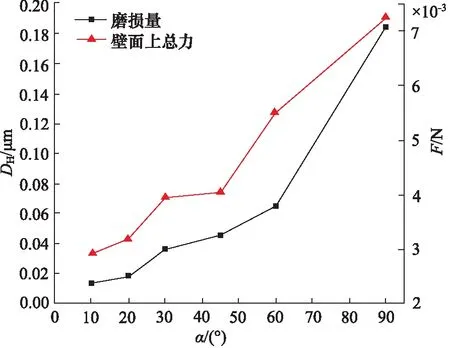
图6 喷嘴磨损量及壁面总力与收缩角之间的关系Fig.6 Relationship between nozzle wear, total wall force and shrinkage angle

为探讨各参数对喷嘴磨损分布区域的影响,将离喷嘴出口处的距离定义为Y,Y=0表示磨损位置在出口处。图7为收缩角对喷嘴表面磨损分布区域的影响,可以发现喷嘴在收缩段与聚焦管的衔接处磨损比较严重,在收缩段喷嘴几乎不发生磨损。其原因主要是在收缩段处流体相压力、速度及湍流动能较低,磨粒速度增加缓慢,运动较为稳定,因此磨粒在收缩段的速度相对较小,与壁面碰撞频率较低,在收缩段磨损很小甚至不发生磨损。

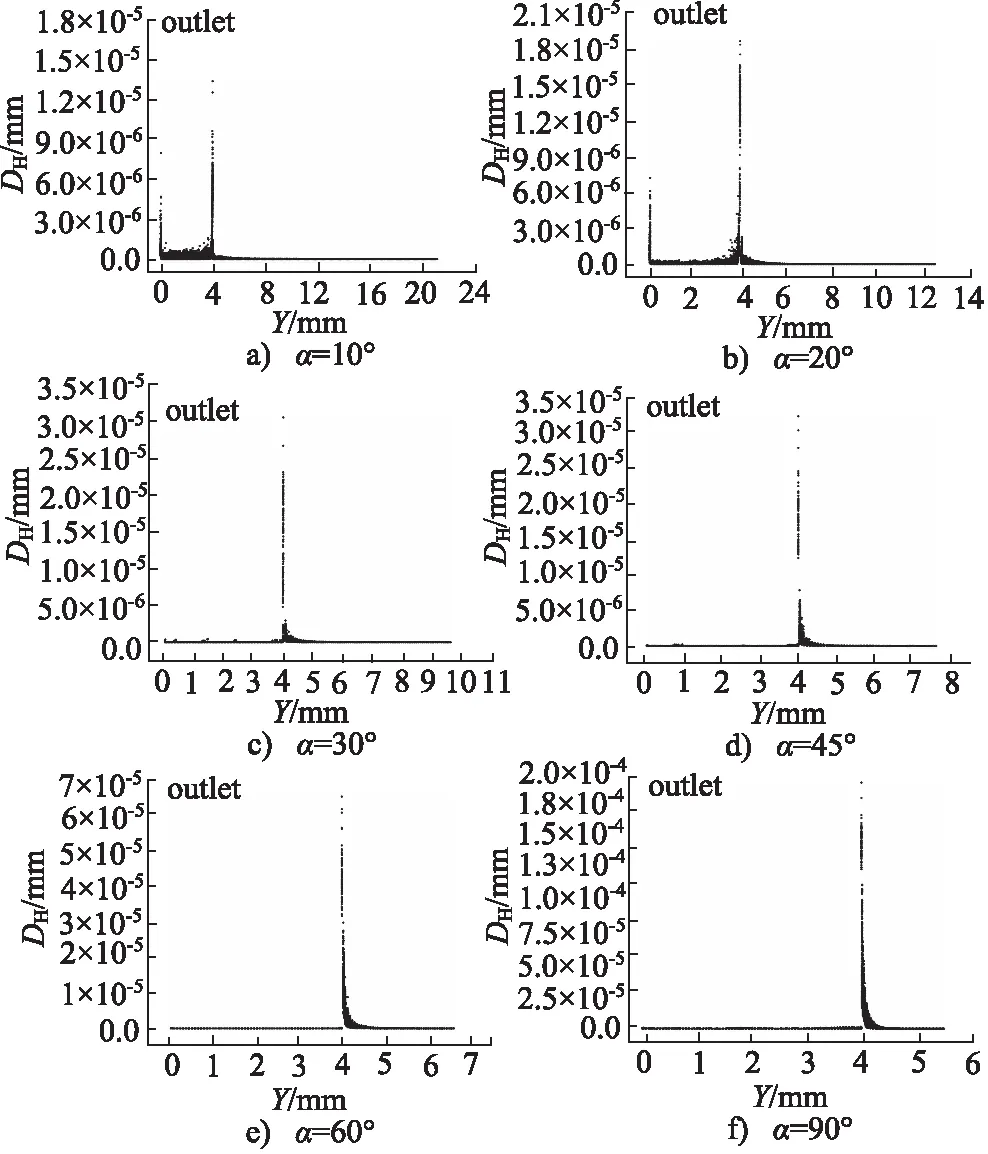
图7 不同收缩角喷嘴内壁磨损分布图Fig.7 Distribution of inner wall wear of nozzles with different shrinkage angles

由射流特性可知,磨粒加速主要发生在过渡区和聚焦管,而由于喷嘴截面变窄,导致在过渡区流场逐渐紊乱,湍流动能及湍流耗散率增加,并且随着收缩角增大,磨粒获得较高的径向速度,从而缩短了两次相邻碰撞的轴向距离,导致磨粒与壁面碰撞频繁,使壁面受到总碰撞力增大,从而使得过渡区产生的磨损较为剧烈,产生第一个磨损峰区。收缩角越小磨粒与壁面碰撞频率越低,而由于喷嘴结构的原因导致混合液进入聚焦管后并不能快速达到稳定状态,因此当收缩角较小时,聚焦管内有微小的磨损,并由于在出口处喷射瞬间空气的吸入,导致在喷嘴出口处会产生第二个磨损峰区。从图7c至图7e可以看出,当收缩角增大时,颗粒与壁面的碰撞角度随之增大,在收缩段颗粒碰撞反弹后更容易进入聚焦管,而同时微粒间相互作用力驱使颗粒有向轴线附近聚集的现象,因此喷嘴聚焦管磨损很小,几乎不发生磨损现象。

2) 长径比对喷嘴磨损的影响

收缩角越大而喷嘴磨损越严重,但收缩角也不宜过小,因为收缩角越小,会影响射流动能,因此在保证射流动能的前提下,以收缩角为20°时为研究对象,研究在系统压力为1.2 MPa,流体黏度为1.01×10-3Pa/s状态下,不同长径比对喷嘴磨损的影响, 其仿真结果如图8所示。

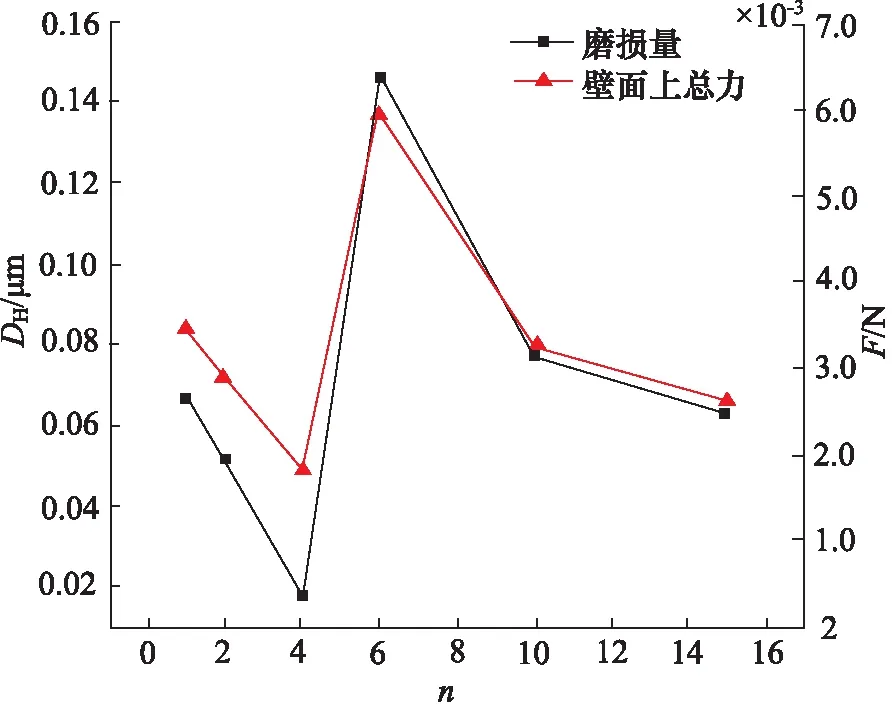
图8 喷嘴磨损量及壁面总力与长径比之间的关系Fig.8 Relationship between nozzle wear, total wall force and aspect ratios

从图中可以发现,当长径比n≤4时,喷嘴磨损与长径比成反比,其原因是由于较短长径比喷嘴,在出口处易受空化影响,部分气体被吸入到喷嘴内部,造成内流场紊乱,颗粒运动复杂,导致较小长径比的喷嘴磨损较为严重,而当长径比增加到4时喷嘴磨损达到最小。当长径比n>4时,喷嘴磨损量呈现先增加后减小的趋势,并在长径比为6时磨损量达到最大,当增加聚焦管长度后,磨粒的径向动能由于与壁面频繁碰撞而逐渐降低,因此当长径比n>4时,适当增加长径比可以有效降低喷嘴磨损,但磨损量仍比长径比为4时的磨损量高。

图9为长径比对喷嘴发生磨损区域分布规律的影响。从图中可以发现,不同长径比对喷嘴磨损程度有影响,而对磨损位置分布并没有太大影响,喷嘴内表面磨损分布均呈现出双峰特性,主要位于出口处以及过渡区,而在收缩段不发生磨损。

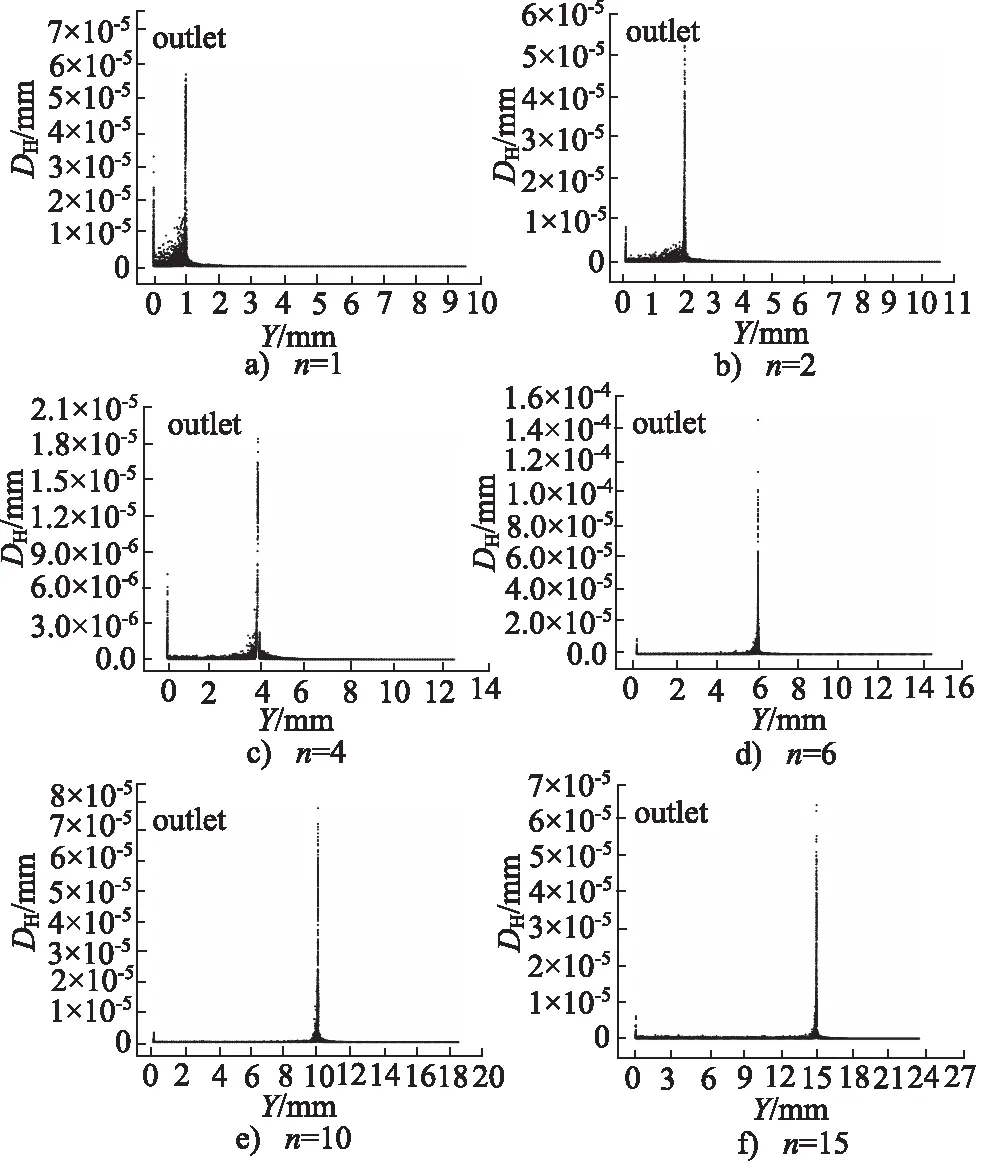
图9 不同长径比喷嘴内壁磨损分布图Fig.9 Distribution of inner wall wear of nozzles with different aspect ratios

对于较小长径比的喷嘴,当射流通过喷嘴出口时与空气发生剧烈能量交换,产生剧烈紊乱扩散,导致在喷嘴出口附近磨粒运动较为紊乱,与壁面碰撞频繁,从而使得较小长径比的喷嘴在聚焦管段的磨损相对严重,如图9a,图9b所示。随着喷嘴长径比增加,聚焦管内壁磨损逐渐减小,其原因是由于磨粒在收缩段与壁面频繁碰撞导致其径向动能减小,同时,在流场作用下,磨粒被流体带动加速,使其以逐渐增大后的轴向速度进入聚焦管,同时由于颗粒间作用力导致颗粒向轴线附近运动,降低颗粒与聚焦管内壁碰撞,碰撞力减小,因此在较大长径比下, 聚焦管内部磨损相对较小。

从仿真数据可以看出,长径比为4时喷嘴磨损最小,而增加或减小喷嘴长径比并不能有效减缓喷嘴磨损。

3.2 喷嘴材料硬度对磨损的影响规律

喷嘴材料特性对磨损也有重要影响,其中以硬度特性影响最大,喷嘴硬度与剪切模量成正比[17],通过设置不同剪切模量来模拟不同材料硬度,以分析材料硬度对磨损的影响规律。

图10为系统工作压力为1.2 MPa,黏度为1.01×10-3Pa/s时不同剪切模量下,喷嘴磨损量及壁面受力的变化趋势图。

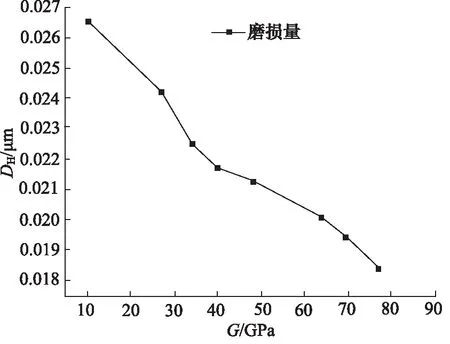
图10 喷嘴磨损量与剪切模量之间的关系Fig.10 Relationship between nozzle wear and shear modulus

从图中可以看出剪切模量G越大喷嘴磨损量越小,当剪切模量为10 GPa时,喷嘴磨损量DH为0.0265 μm,剪切模量为48 GPa时,喷嘴磨损量为0.0213 μm,当剪切模量增加到77 GPa时,喷嘴磨损量降低为0.0184 μm,相比于剪切模量小于48 GPa时,磨损量约降低了一倍。分析原因是当剪切模量较小时,喷嘴的硬度较低,耐冲蚀能力较低,因此磨损较快,而随着材料剪切模量提高,喷嘴硬度提高,喷嘴耐磨性提高,喷嘴磨损量降低相对缓慢。

提高喷嘴材料硬度可以缓解喷嘴磨损,目前常见用于制造喷嘴的材料有陶瓷、硬质合金和人造宝石等,而提高喷嘴的硬度会增加喷嘴加工难度及加工成本,因此可以选择表面镀层或热处理方式提高喷嘴内表面耐磨性,如刘占鏖等[30]利用类金刚石薄膜对喷嘴芯进行镀层,其硬度由2400 HV提升至3500 HV,有效提高了喷嘴耐磨性。

在喷嘴材料剪切模量不同情况下,喷嘴内表面磨损分布呈双峰特性,如图11所示,发生峰值区主要位于喷嘴过渡区和聚焦管出口处。此外,从图中可以看出,不同剪切模量下喷嘴磨损分布并没有明显的区别,结果表明喷嘴材料的硬度基本上不会影响喷嘴磨损分布,但会影响喷嘴磨损程度。

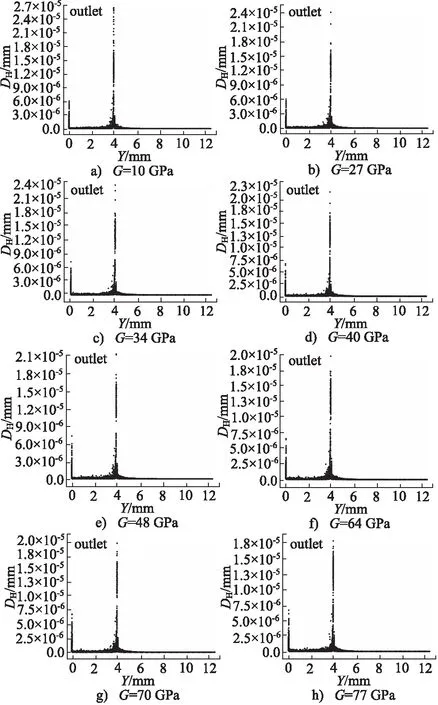
图11 不同喷嘴剪切模量喷嘴内壁磨损分布图Fig.11 Distribution of inner wall wear of nozzles with different shear modulus

3.3 工艺参数对喷嘴磨损的影响

除喷嘴结构外,系统参数以及工艺参数对喷嘴磨损也存在着影响,影响较为显著的有工作压力、流体黏度以及颗粒特性等。为探讨系统工作压力以及液体黏度对喷嘴磨损的影响规律,本节选取压力为0.6, 0.8, 1.0, 1.2 MPa及流体黏度为1.01×10-3Pa/s和2.82×10-3Pa/s进行探究。如图12所示显示了剪切模量为70 GPa,长径比为4,收缩角为20°时系统工作压力与液体黏度对喷嘴磨损及分布规律的影响。

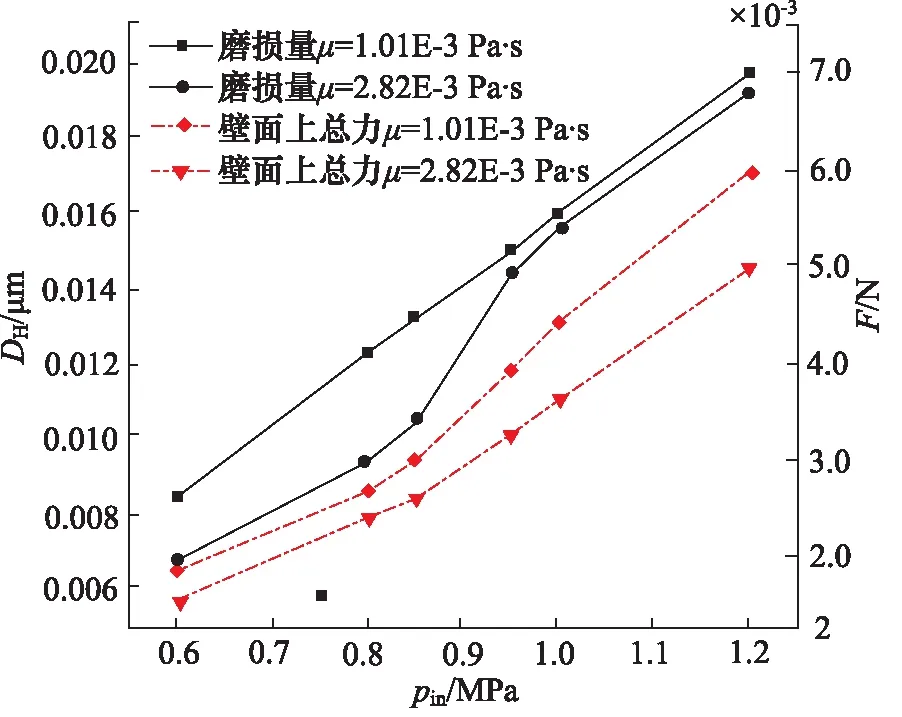
图12 工艺参数对喷嘴磨损以及壁面受力的影响Fig.12 Effect of process parameters on nozzle wear and wall force

从图中发现喷嘴磨损量DH随着工作压力pin增大而增加。由式(12)射流压力与射流速度的关系可知,当系统工作压力增加,流体速度和磨粒动能将得到提高,喷嘴内颗粒与壁面发生频繁碰撞,导致壁面受力F以及喷嘴磨损量增加。

(12)

此外,从图12中可以发现液体黏度增加会降低喷嘴磨损量,原因是由于黏度增大, 黏性力逐渐起作用,颗粒与流体间的滑移速度较小,因此在黏度较大的溶液中,磨料具有较高的动能,并且黏度增加使磨料在管道内分布相对均匀,因此壁面磨损相对降低。

从图12中发现在黏度为2.82×10-3Pa/s时,当工作压力从0.8 MPa增加到1.0 MPa时,喷嘴磨损量呈现陡然上升的趋势,分析原因是由于压力升高,流场在变截面处发生剧烈紊乱,同时由于在相对较高黏度的流场中磨粒具有较好的跟随性,因此相比低压低黏度下磨料的运动特性,磨粒获得更高动能,磨料与壁面碰撞更严重。

系统工作压力以及黏度对喷嘴磨损分布规律的影响如图13所示。

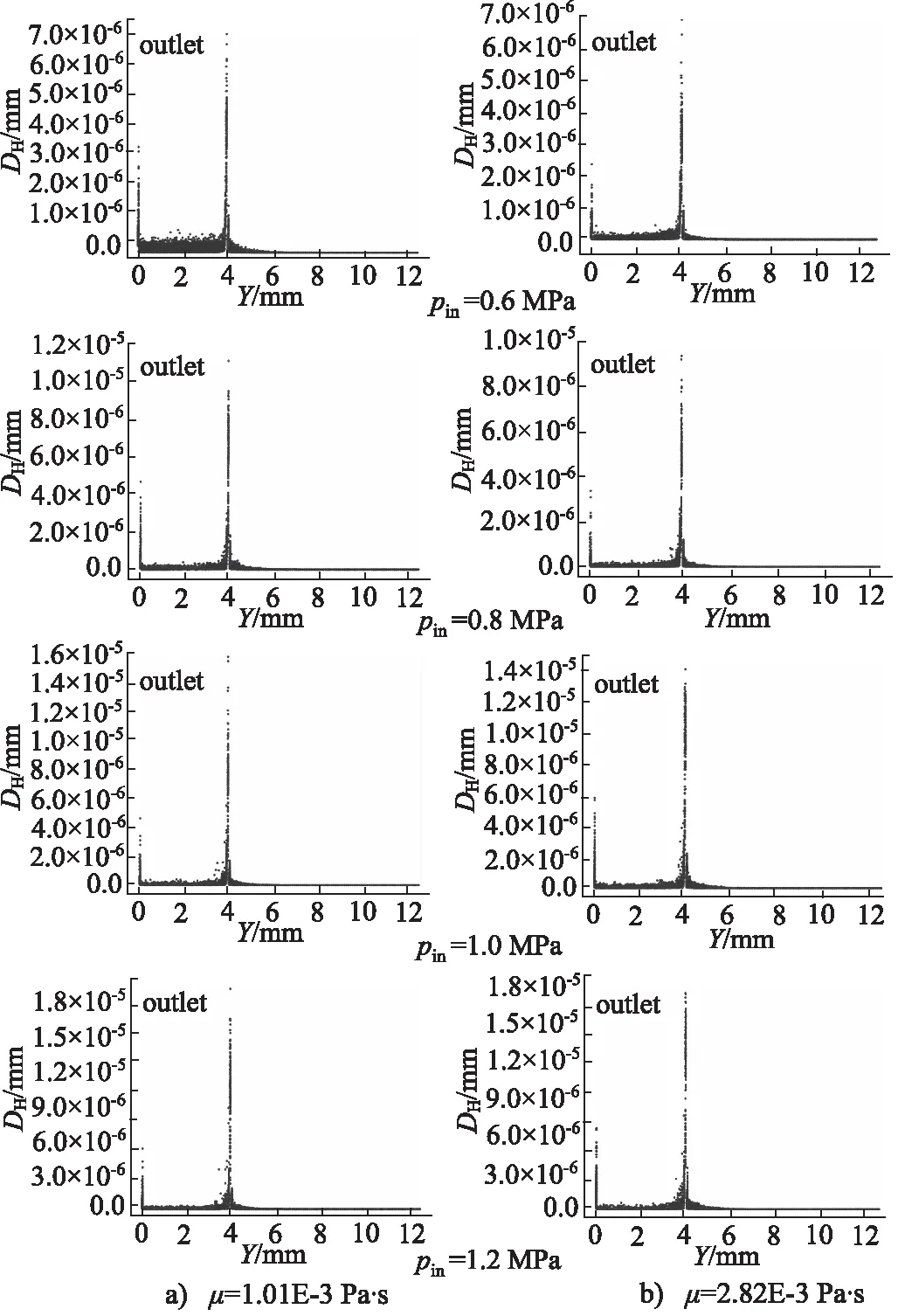
图13 不同工作压力及流体黏度下喷嘴磨损分布图Fig.13 Nozzle wear distribution under different working pressure and fluid viscosity

从图中可以看出,两种不同黏度下喷嘴磨损分布均呈现出两个峰值,其中峰值主要位于喷嘴过渡区和出口位置,喷嘴聚焦管内也存在微量磨损。当压力为1.2 MPa时,相对于流体黏度为1.01×10-3Pa/s,黏度为2.82×10-3Pa/s时喷嘴最大磨损量降低,因此得出工作压力以及流体黏度的改变并不会引起喷嘴磨损分布位置变化,工作压力以及流体黏度对喷嘴的磨损程度有影响,而对喷嘴发生磨损位置分布并无影响。

4 结论

本研究基于CFD-DEM方法和Oka磨损模型建立数学计算模型,通过离散元法考虑颗粒间及颗粒与壁间的相互作用,探讨了不同结构喷嘴及工艺参数对磨料水射流抛光喷嘴磨损和磨损分布规律的影响,结论如下:

(1) 喷嘴收缩角对喷嘴磨损及分布规律有影响。当喷嘴长径比为4,喷嘴收缩角从10°逐渐增加到90°时,喷嘴逐渐发生严重磨损。此外,喷嘴磨损分布随着收缩角的增大,由双峰特性转变为单峰,主要磨损区域发生在过渡区;

(2) 对于收缩角为20°的喷嘴结构,增加或减小喷嘴长径比并不能降低喷嘴磨损,当长径比为4时喷嘴磨损量最小,而改变喷嘴长径比对喷嘴磨损分布规律并没有影响;

(3) 仿真结果表明,相对于剪切模量小于48 GPa时,当剪切模量大于48 GPa时磨损量约降低一倍,且磨损量降低较缓,但对喷嘴磨损分布规律均呈现双峰特性;

(4) 改变系统工作压力以及流体黏度会直接影响喷嘴磨损情况,而对喷嘴磨损分布规律并没有影响。系统工作压力越大磨损越严重,而适当增加流体黏度可以减缓喷嘴磨损。

综上,喷嘴的收缩角、长径比、剪切模量以及工艺参数对喷嘴磨损量均有影响,而不同喷嘴结构会影响喷嘴磨损峰值的区域,剪切模量以及工艺参数对喷嘴内表面磨损分布规律基本上无影响。因此,为防止喷嘴磨加剧,延缓喷嘴使用寿命,可选择较高硬度的材料制作喷嘴,同时喷嘴收缩角和长径比不宜选择过大,并且可适当加入添加剂增大液体的黏性来降低喷嘴的磨损。