带形状参数的双三次Bezier三角曲面的光滑拼接

孙明灿, 师晶

(闽南理工学院 信息管理学院,福建 石狮 362700)

0 引言

在计算机辅助几何设计(CAGD)中,Bezier曲线曲面由于具有图像直观、易于理解和计算高效等优点被广泛应用于动画制作、电子信息、生物技术及工业制造等领域中[1].但Bezier曲线曲面在曲面造型中也存在一些不足,如图形会随着控制顶点的改变而发生变化,且它还无法精确表示一些二次曲线曲面的形状.为解决Bezier曲线曲面在曲面造型中存在的这些问题,一些学者对其性质进行了研究,并取得了一些良好成果.例如:文献[2]的作者提出了一种能够保持参数连续性的多曲面变形技术,该变形技术不仅误差可控,而且还可使边界处的节点矢量在不必相同的条件下即可实现曲面的光滑拼接.文献[3]的作者给出了一种利用曲面边界线构建拼接曲面的方法,该方法不仅可用函数精确地表示三次规则曲面和自由曲面,而且还具有独立的跨界导矢和约束条件.文献[4]的作者在文献[3]的基础上,利用Coons曲面的设计原理构造了一个可满足C1连续的CNSBS曲面,研究表明该曲面不仅具有独立的跨界导矢和约束条件,而且还具有B样条曲面的性质.文献[5]的作者基于最小二乘法和参数优化方法提出了一种样条曲面光滑拼接的方法,该方法不仅可有效避免曲面错位,而且还可最小化控制顶点的数量.文献[6]的作者讨论了一类广义Bezier曲线离散造型的细分算法,该算法构造的广义Bezier曲线具有直观性、可调性,因此可推广到相应的张量积曲面造型中.文献[7]的作者讨论了一种基于几何约束的代数曲线,研究表明该曲线不仅保留了样条曲线的几何性质,而且具有良好的逼近性和局部形状可调性.文献[8]的作者给出了一类四次三角Bezier曲线的性质和应用,研究显示该曲线不须改变控制多边形即可生成非对称的图形.基于上述研究,本文定义了一种带形状参数的双三次Bezier三角曲面,并给出了该曲面基函数和曲面的性质以及曲面间G1光滑拼接的定理及拼接算法.实例计算表明,本文算法不仅在不同方向上可实现参数的连续性,而且还可有效提高曲面形状的可控性.

1 带形状参数的双三次Bezier三角曲面

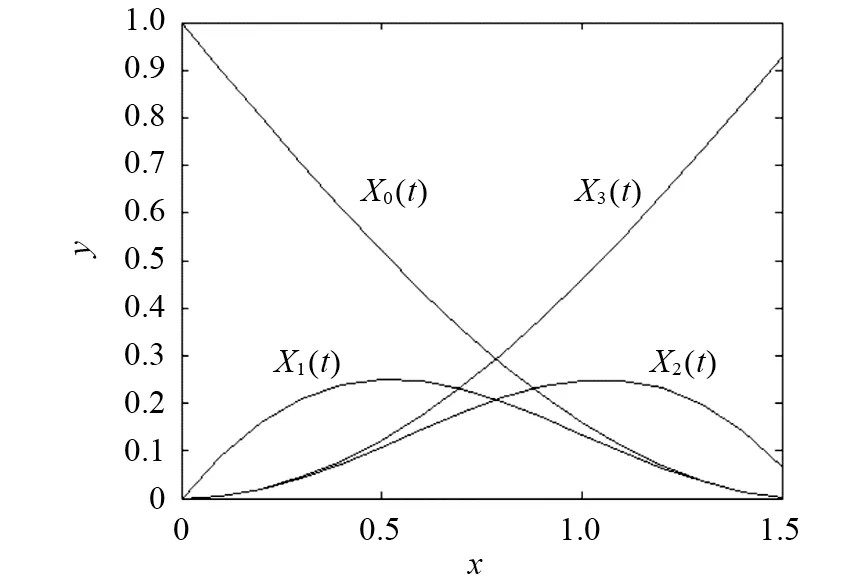
图1 基函数的图形

2)几何不变性,即曲线p(t)的形状仅与控制顶点Pi(i= 0,1,2,3)有关,而与坐标系的选取无关.

证明对控制顶点为Pi(i= 0,1,2,3)的曲线p1(t)进行线性变换和平移变换后,得控制顶点为Qi(i=0,1,2,3)的曲线p2(t)为:

式中:M为线性变换,N为平移变换.由上式可知,曲线具有几何不变性.

3)凸包性,即曲线p(t)落在由控制顶点Pi(i= 0,1,2,3)构成的凸包内.

其次证明变差缩减性质成立.设直线L与控制多边形P0P1P2P3的边PiPi+1交于点Q,直线L与控制多边形P0P1P2P3的交点个数为m,且边PiPi+1的法向量为v.由于控制顶点Pi和Pi+1分别位于直线L的两侧,所以v·(Pi-Q)和v·(Pi+1-Q)的符号相反,进而有:

5)保凸性,即曲线p(t)具有保凸性.

证明由变差缩减性可知,当控制多边形为凸多边形时,平面内任一直线与控制多边形的交点数最多为2.由此可得曲线p(t)与任一直线的交点数最多为2,故曲线p(t)具有保凸性.

6)逼近性,即:当形状参数α变大时,曲线p(t)更加逼近控制多边形的边P1P2;当形状参数α变小时,曲线p(t)更加逼近控制多边形的边P0P3.当形状参数α取不同值时,带形状参数的三次Bezier三角曲线p(t)的图形如图2所示.

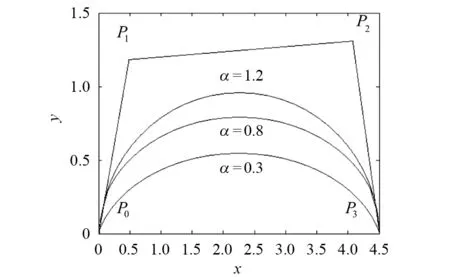
图2 带形状参数的三次Bezier三角曲线p(t)的图形

定义3在R3空间中给定16个控制顶点Pij(i,j= 0,1,2,3),α1,α2∈(0,2],定义带形状参数的双三次Bezier三角曲面为:

其中Xi(u,α1)和Xj(v,α2)与式(1)定义的基函数相同,α1和α2是曲面的两个形状参数.

带形状参数的双三次Bezier三角曲面S(u,v;α1,α2)具有以下性质:

证明由带形状参数的三次Bezier三角曲线p(t)的端点性质和定义3可得:

由上式可知插值性得证.

2)边界性和凸包性,即曲面S(u,v;α1,α2)位于由控制顶点Pij(i,j= 0,1,2,3)生成的凸包内,且4条边界曲线均为三次Bezier三角曲线.4条边界曲线分别为:

证明由带形状参数的三次Bezier三角曲线p(t)的端点性质和定义3可得:

由上式可知边界性和凸包性得证.

3)几何不变性,即曲面S(u,v;α1,α2)的数学表示式及其形状不依赖于坐标系的选择.

证明因证明过程与曲线p(t)的几何不变性的证明过程类似,故本文在此省略.

4)表示唯一性,即若有两张曲面S(u,v;α1,α2)相同,则它们的控制顶点和形状参数相同;反之,它们的控制顶点和形状参数不同.

证明由式(3)可知,曲面S(u,v;α1,α2)的表示唯一性显然成立.

5)形状可调性,即曲面S(u,v;α1,α2)的形状参数对曲面的形状具有调节作用.

证明由于曲面S(u,v;α1,α2)带有两个形状参数α1和α2,因此根据曲线p(t)的逼近性可知:在控制顶点Pij(i,j= 0,1,2,3)不变的情况下,通过选取不同的α1值和α2值可调整曲面的形状.当α1=α2= 0时,曲面S(u,v;α1,α2)是定义在三角域上的三次Bezier三角曲面,由此可知定义在三角域上的三次Bezier三角曲面是曲面S(u,v;α1,α2)的一个特殊情况.图3为形状参数α1和α2取不同值时的曲面图.

图3 形状参数α1 和α2 取不同值时的曲面图

2 形状参数的几何意义

为方便设计者调整曲面S(u,v;α1,α2)的形状,本文对两个形状参数α1和α2的几何意义进行分析,即分析当其中一个形状参数发生改变或两个形状参数均发生改变时,曲面形状所发生变化的规律.

定理1在带形状参数的双三次Bezier三角曲面S(u,v;α1,α2)中,当控制顶点Pij(i,j=0,1,2,3)不变时,有:①若保持其中一个形状参数不变,而增大(或减小)另一个形状参数,则曲面会逐渐靠近(或远离)控制网格;②若同时增大(或减小)两个形状参数,则曲面会逐渐靠近(或远离)控制网格.

证明本文采用文献[9]中的证明方法证明定理1中的①.不失一般性,假设形状参数α2不变,则曲面S(u,v;α1,α2)的基函数Xi(t)(i= 0,1,2,3)对形状参数α1求导可得:

由上式可知,当形状参数α2不变而α1增大时,X1(t)和X2(t)均增大,而X0(t)和X3(t)均减小.再由式(3)可知,当形状参数α2不变而α1增大时,曲面S(u,v;α1,α2)图靠近控制顶点P1j和P2j(j= 0,1,2,3),同时远离控制顶点P0j和P3j(j= 0,1,2,3).另外,由于P1j和P2j(j= 0,1,2,3)是位于曲面S(u,v;α1,α2)中间位置的控制顶点,所以当曲面S(u,v;α1,α2)图靠近控制顶点P1j和P2j(j= 0,1,2,3)时曲面S(u,v;α1,α2)图靠近控制网格.同理,当形状参数α2不变而α1减小时,曲面S(u,v;α1,α2)图远离控制网格.

因证明定理1中的②的过程与证明定理1中的①的过程类似,故本文在此省略.

3 曲面的G1 拼接定理

其中:两曲面的控制顶点分别为Pij和Qij(i,j= 0,1,2,3);形状参数α1,α2,λ1,λ2∈(0,2];Xi(u,α1)、Xj(v,α2)、Xi(u,λ1)和Xj(v,λ2)与式(1)定义的基函数相同.

定理3两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)满足u向与u向G1拼接的充要条件是:

推论11)若两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)在u向与u向上有公共的边界,则仅改变形状参数α2和λ2的值仍能使两张曲面保持G0拼接.

2)若两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)满足u向与u向G1拼接,则修改形状参数α1、α2、λ1和λ2可改变拼接曲面的整体形状,修改法矢模比例因子μ可改变拼接曲面的局部形状.

证明首先证明1).若两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)在u向与u向上有公共的边界,则由定理3中的条件2)可知两张曲面的G0拼接条件仅与α1和λ1有关,而与α2和λ2无关.所以,若仅改变形状参数α2和λ2的值仍能使两张曲面保持G0拼接.

因2)的证明过程与1)的证明过程类似,故本文在此省略.

定理4两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)满足v向与v向G1拼接的充要条件是:

推论21)若两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)在v向与v向上有公共的边界,则仅改变形状参数α1和λ1的值仍能使两张曲面保持G0拼接.

2)若两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)满足v向与v向G1拼接,则修改形状参数α1、α2、λ1和λ2可改变拼接曲面的整体形状,修改法矢模比例因子μ可改变拼接曲面的局部形状.

证明因证明过程与推论1的证明过程类似,故本文在此省略.

定理5两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)满足u向与v向G1拼接的充要条件是:

证明因证明过程与定理1和定理2的证明过程类似,故本文在此省略.

推论31)若两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)在u向与v向上有公共的边界,则仅改变形状参数α2和λ1的值仍能使两张曲面保持G0拼接.

2)若两张双三次Bezier三角曲面S1(u,v;α1,α2)和S2(u,v;λ1,λ2)满足u向与v向G1拼接,则修改形状参数α1、α2、λ1和λ2可改变拼接曲面的整体形状,修改法矢模比例因子μ可改变拼接曲面的局部形状.

证明因证明过程与推论1的证明过程类似,故本文在此省略.

4 曲面拼接算法的实现

带形状参数的双三次Bezier三角曲面的拼接算法如下:

步骤1 选定待拼接曲面的16个控制顶点Pij(i,j= 0,1,2,3)及形状参数α1和α2,并根据双三次Bezier三角曲面方程计算出第1张待拼接曲面S1(u,v;α1,α2);

步骤2 计算出曲面S1(u,v;α1,α2)公共边界线的4个控制顶点,并根据G1拼接定理确定相邻曲面的其余12个控制顶点Qij(i= 0,1,2,3;j= 1,2,3)及形状参数λ1和λ2,由此得到第2张待拼接曲面S2(u,v;λ1,λ2);

步骤3 如果待拼接曲面数大于2,则转至步骤2,直至生成所有待拼接曲面后再执行下一步;否则,直接执行下一步;

步骤4 通过修改各拼接曲面片的形状参数及法矢模比例因子调整拼接曲面的形状,以此获得满意的图形.

5 计算实例

构造碗曲面模型时,因需要多个曲面才能拼接而成,因此本文根据选定的16个控制顶点Pij(i,j= 0,1,2,3)首先计算出第1张待拼接曲面S1(u,v;α1,α2).16个控制顶点分别为:

然后再根据曲面S1(u,v;α1,α2)与第2张待拼接曲面S2(u,v;λ1,λ2)的公共边界线的4个控制顶点Pi3(i= 0,1,2,3)和曲面S2(u,v;λ1,λ2)的其余12个控制顶点Qij(i= 0,1,2,3;j= 1,2,3)计算出第2张待拼接曲面S2(u,v;λ1,λ2).曲面S2(u,v;λ1,λ2)的其余12个控制顶点分别为:

重复以上步骤,最终可生成如下4张待拼接曲面:

由于上述4张曲面的任意2个相邻曲面在u向具有公共的边界线,所以上述4张曲面的任意2个相邻曲面均满足u向与u向的G0拼接条件,且这4张曲面的形状参数满足α1=λ1=β1=γ1,如图4所示.

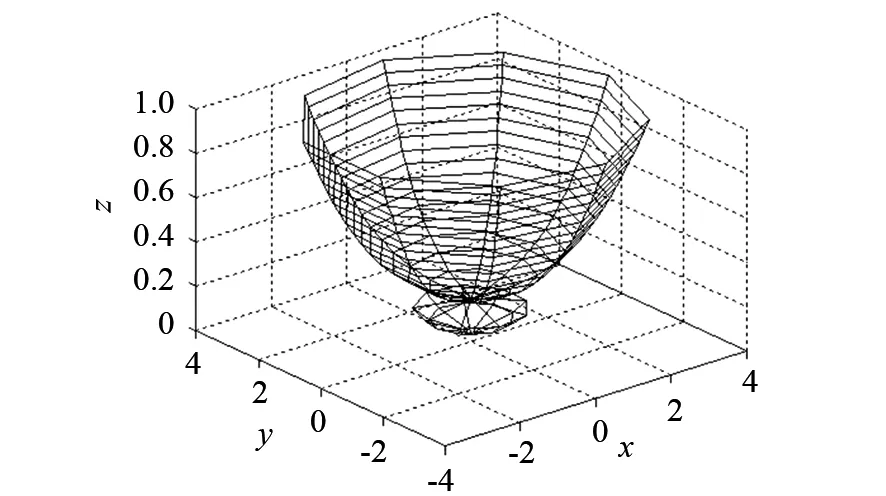
图4 碗曲面G0 拼接的网格模型

当相邻曲面满足u向与u向的G1拼接时,由定理3可知.所以,通过修改法矢模比例因子μ可改变拼接曲面的局部形状.不同法矢模比例因子下的碗曲面G1拼接的网格模型如图5所示.由定理3和图5可得:法矢模比例因子越大,相邻公共边界线的两排控制顶点越靠近边界线处的控制顶点;法矢模比例因子越小,相邻公共边界线的两排控制顶点越远离边界线处的控制顶点.

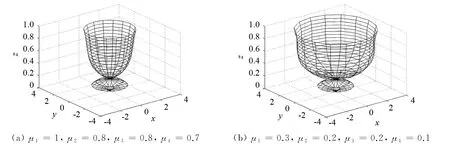
图5 不同法矢模比例因子下的碗曲面G1 拼接的网格模型

另外,由曲面的形状可调性和定理1可知,修改形状参数可改变曲面的整体形状,即:当形状参数增大或减小时,曲面从整体上逐渐靠近或远离控制网格.不同形状参数下的碗曲面G1拼接的网格模型如图6所示.

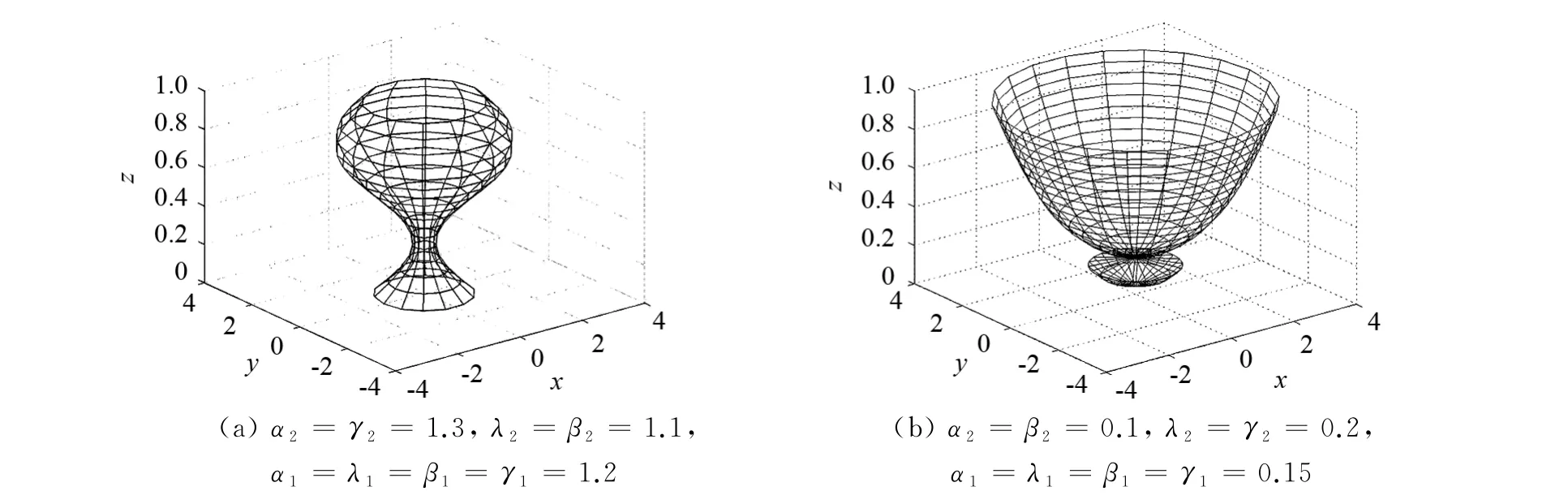
图6 不同形状参数下的碗曲面G1 拼接的网格模型

6 结束语

本文研究了带形状参数的双三次Bezier三角曲面的光滑拼接,该曲面不仅保留了传统Bezier曲面的一些优良性质(插值性、边界性质、凸包性、几何不变性等),而且在不改变控制顶点的条件下可通过形状参数调节曲面形状.为提高Bezier曲面在复杂曲面造型中的构图能力,本文给出了带形状参数的双三次Bezier三角曲面的u向与u向、v向与v向、u向与v向间的G1拼接定理及其算法.实例计算显示,曲面的形状参数和法矢模比例因子可分别调整曲面的整体形状和局部形状,并且其几何意义明显.即:在给定范围内,形状参数越大,曲面在整体上越靠近控制网格;法矢模比例因子越大,相邻公共边界线的两排控制顶点越靠近边界线处的控制顶点.本文研究结果有效解决了Bezier曲面难以进行局部调节的缺点.在今后的工作中,我们将对高次曲线曲面的光滑拼接进行研究.