一种合理利用先验信息的新平差方法
刘 萍 谢雪梅
1 深圳市龙华区福城街道办事处土地整备中心,深圳市观光路1354号,518000 2 中南林业科技大学土木工程学院,长沙市韶山南路498号,410004
由Bayes估计原理可知,当先验信息和观测信息均可靠时,参数最小二乘估计满足无偏、一致、有效性[1-2]。但当先验信息不可靠时,先验信息和观测信息对参数解的贡献不同。这时需要给先验信息赋予一个权值以平衡观测信息与先验信息的权比,从而控制先验信息对参数解的影响[3]。许多学者研究了先验信息的权值问题,如Durbin[4]和Theil等[5-6]提出混合估计方法,Schaffrin等[7]在混合估计的基础上提出加权混合估计。这些算法大多注重于计算效率和估计的优良性,没有提供先验信息权值的计算方法,不能直接用于大地测量数据处理。平衡损失函数综合考虑模型拟合优度与参数估计的精度,建立了一个新的参数估计准则[2,8]。在统计决策上,它是使均方误差达到最小的估计[8]。由于现有的算法无法计算先验信息权值,平衡估计方法在测绘工程中的应用较少。本文基于Bayes估计原理,在平衡估计准则的基础上,研究观测信息可靠时先验信息对平差结果的影响,建立先验信息的判别统计量,给出一个自适应计算平衡因子的方法,控制不准确的先验信息对参数解的影响。
1 参数的Bayes估计
一般平差模型可写为:
L=AX+e
(1)
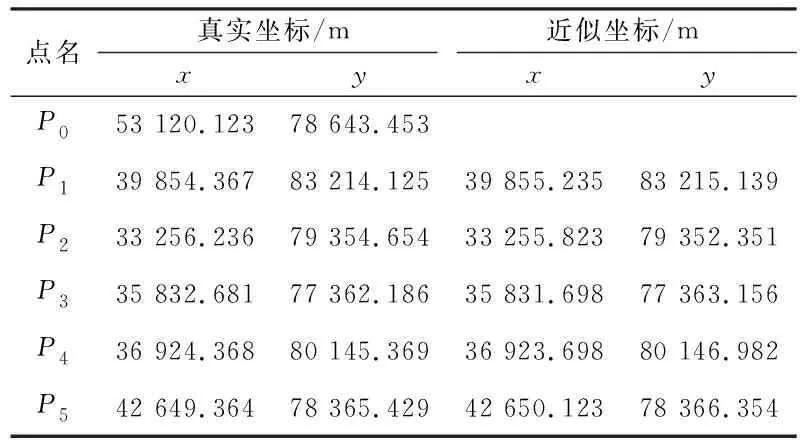
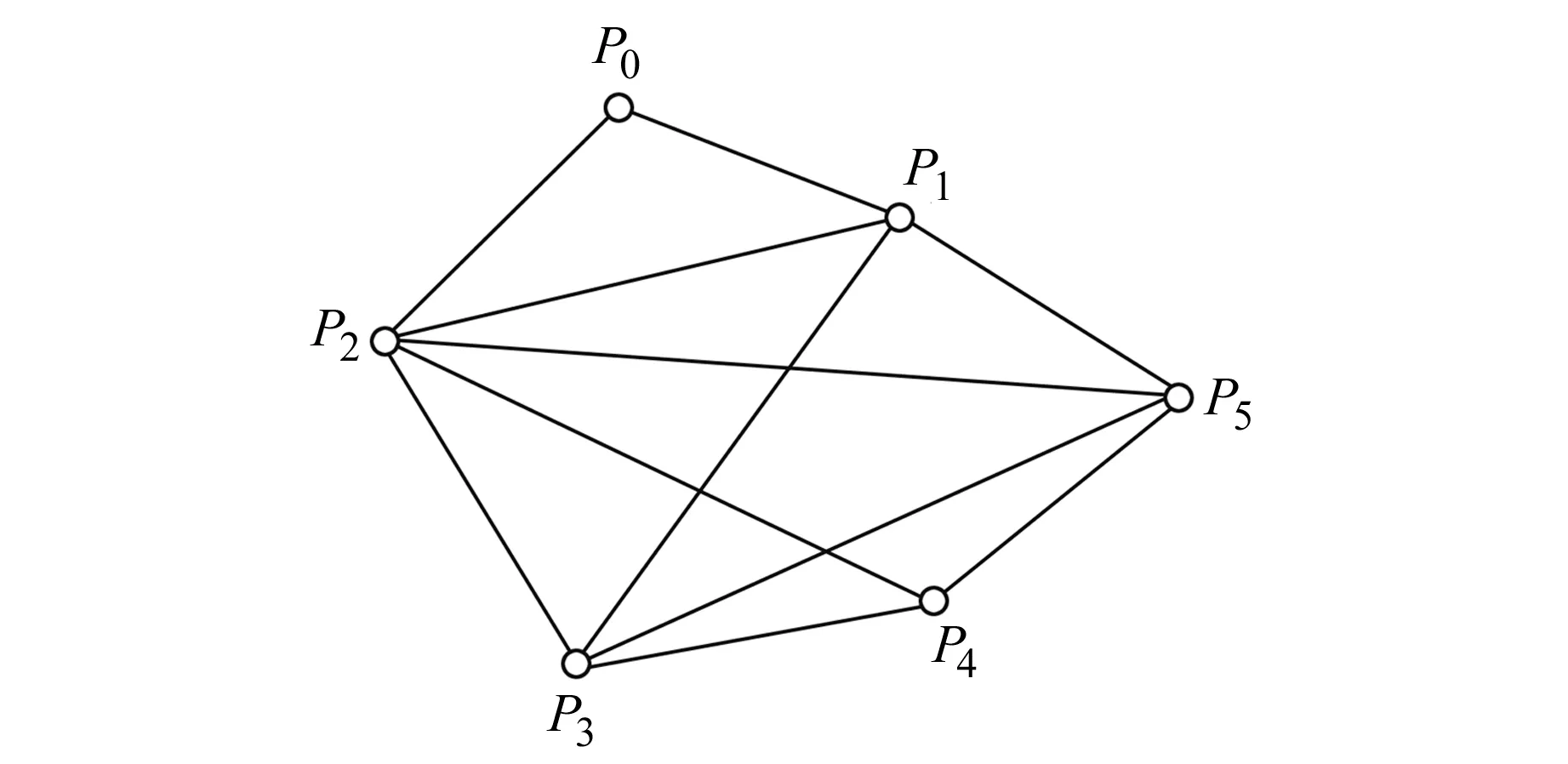
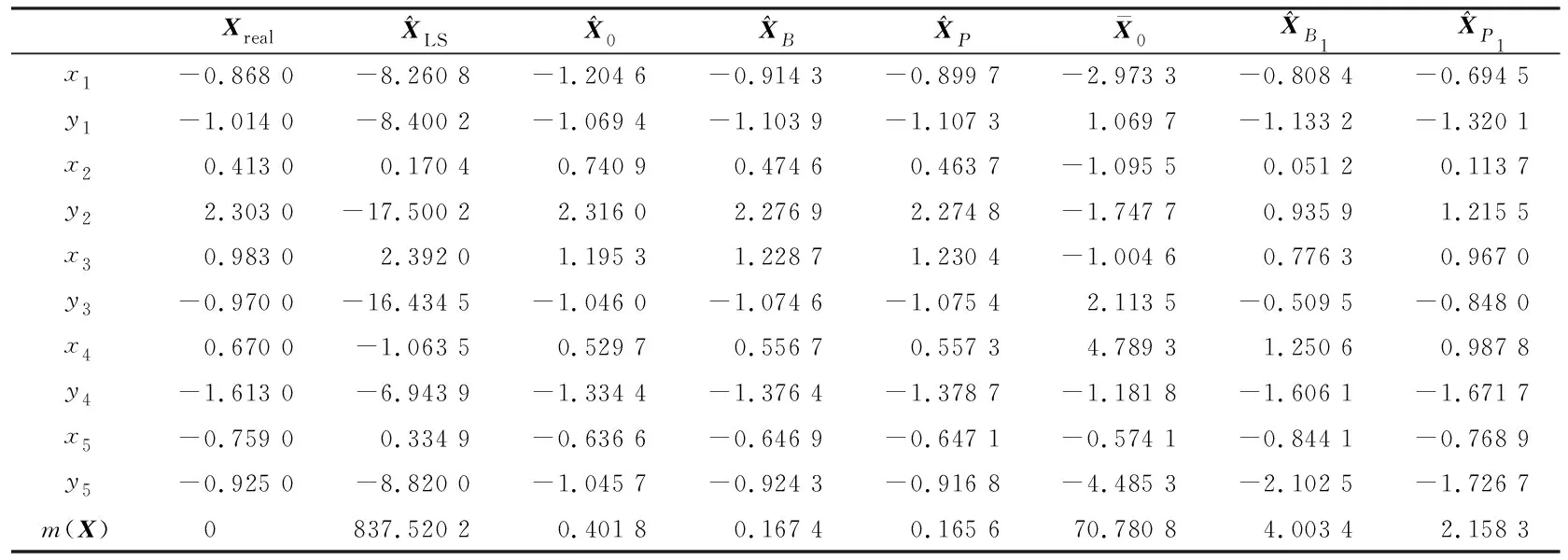
式中,A为m×n维系数矩阵,rank(A) E(X)=X0,cov(X)=ΣX=S-1 (2) 式中,X0是已知向量;ΣX为已知正定矩阵。观测向量L的条件分布f(L|X)=N(AX,Σ),可得到参数向量X的验后分布为[9]: (L-AX)TP(L-AX)]} (3) 式中,∝表示成正比例关系。由Bayes估计的准则[10],f(X|L)=max,因此有: (L-AX)TP(L-AX)+ (X-X0)TS(X-X0)=min (4) 由式(4)对X求极值,由矩阵的微分法得: (ATPA+S)X=ATPL+SX0 (5) (6) 可以看出,X的Bayes线性无偏估计是先验信息X0和观测信息L的一个线性组合。当观测信息的先验信息和观测信息可靠(观测误差服从正态分布)时,参数极大验后估计是一个线性无偏最小方差估计[3]。 为了平衡观测信息与先验信息的权比,控制不准确的先验信息对参数解的影响,在式(4)的基础上给先验信息赋予一个权值: (L-AX)TP(L-AX)+ α(X-X0)TS(X-X0)=min (7) 对参数向量X求极值: -ATP(L-AX)+αS(X-X0)=0 (8) (9) (10) (11) (12) 下面是根据统计量构造的一个两段函数平衡因子,其原理类似于Huber函数[11]: (13) 为了验证平衡估计在参数解算中的效果,设计如下算例:设有一测边网(图1),P0为起算点,P1、P2、P3、P4、P5的真实坐标已知(表1),边长的观测值是利用真实坐标与随机误差计算得到的,误差范围为(-0.05 m, 0.05 m),观测边长视为同精度(表2)。相对于近似坐标的改正数构成的未知向量为X=[x1,y1,x2,y2,x3,y3,x4,y4,x5,y5]T。 表1 点的坐标Tab.1 Coordinates of the points 图1 测边网Fig.1 Distance-measuring network 对观测方程进行线性化可以得到相应平差模型L=AX+e,其中,A和L为别为: L=(-0.158 9,0.436 8,-2.535 2,-1.430 0,-0.041 1,-0.774 4, 2.870 3,0.058 1,-0.637 9,-0.360 0,-1.774 4,-1.154 8)T 计算结果见表3,算例分析与说明如下。 表3 几种平差算法的比较Tab.3 Comparison of several adjustment methods 2)表3中的m(X)表示如下的均方误差: 式中,Xreal为真值。 5)利用平衡估计准则可以很好地改善参数估计的性能,提高参数估计的准确性。α1=0.919 9说明当先验信息准确度高时,平衡因子给予观测信息的权大;α2=0.587 9说明当先验信息准确度低时,平衡因子给予观测信息更小的权,验证了本文方法具有按照先验信息自适应调节平衡的功能。2 平衡准则下的参数估计
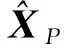
3 平衡因子的计算
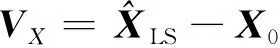

4 模拟算例
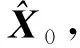
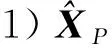



5 结 语