改进天鹰优化器优化Elman神经网络模型预测管道蜡沉积速率

陈卓, 刘波, 张源, 杨云博, 田洋阳

(1.中国石化西北油田分公司采油二厂, 乌鲁木齐 830016; 2.国家管网北方管道长庆输油气分公司, 银川 750001;3.中国石油长庆油田分公司第六采气厂, 西安 710021; 4.中国石油长庆油田长北作业分公司, 西安 710018;5.西安石油大学石油工程学院, 西安 710065)

原油管道输送因其具有输送量大、经济环保、成本较低等优点,是中国目前主要的原油输送方式。但国产原油大多具有高黏、易凝且含蜡量高等特性,在管输过程中,随着管道压力、温度等条件的变化,极易导致原油中蜡、胶质及沥青质等重质组分以固体形式析出,并在管壁上形成蜡沉积[1-2]。管壁结蜡会使得管道有效流通面积减小、流通阻力增大、输送能力降低,严重时甚至堵塞管道,清管作业时易发生清管器卡堵等故障[3]。因此,建立蜡沉积模型预测实际管输过程中的蜡沉积情况至关重要。

随着计算机科学的不断发展,基于神经网络、微粒群算法等智能算法对管道蜡沉积厚度进行预测的研究应用越来越广泛,其不需要探究影响管道结蜡厚度的具体机理,主要是通过机器学习的方法对大量的实验数据进行处理,训练模拟蜡沉积速率同各影响因素之间的关系,确定不同工况状态下的管道结蜡厚度, 进而对管道蜡沉积速率进行预测[4]。周诗岽等[5]考虑了原油的动力黏度、管壁处剪切应力、管壁处温度梯度和管壁处蜡分子浓度梯度4个因素对蜡沉积速率的影响,构建了误差反向传播神经网络模型(back propagation neural networks, BPNN),并证实了所建模型的有效性。田震等[6]综合考虑了7个因素对管道蜡沉积速率的影响,建立了预测蜡沉积速率的7-10-1三层BPNN模型。作者指出,BPNN模型存在一些固有的缺陷,其会很大程度上影响模型的预测性能。Xie等[7]建立了径向基函数神经网络并预测了蜡沉积速率,结果表明该模型的相对误差仅为1.5%。王磊等[8]建立了支持向量机模型来预测管道的蜡沉积速率,作者指出使用(radial basis function, RBF)神经网络作为核函数时,不同的惩罚因子C、核函数参数g组合对预测结果影响较大。以上学者们基于所建模型获得的预测结果虽与真实值均较为吻合,但受限于优化算法和神经网络自身局限性,可能导致针对多因素、高维度问题导致在管道蜡沉积速率预测过程中出现泛化能力不足、预测效果不佳等问题。

Elman神经网络是一种典型的局部回归网络,目前已在很多领域得到了应用。其在应用过程中,往往存在泛化能力不足、易陷入极小点的缺陷。天鹰优化器(aquila optimizer,AO)是一种新型元启发式优化算法,其主要灵感来源于天鹰在捕捉猎物过程中的自然界行为,具有全局搜索能力强、求解精度较高的优点。但其与传统的元启发式算法都存在相同缺陷,即在寻优过程中无法在全局与局部搜索之间取得最佳平衡。针对传统Elman神经网络(Elman neural network, ENN)模型与天鹰优化器的不足,引入鲸鱼优化算法的狩猎策略对天鹰优化器的局部搜索能力进行改进,提出一种基于改进天鹰优化器(improved aquila optimizer, IAO)的ENN模型,并通过室内结蜡实验数据验证了所建模型的有效性,其研究结果对于结蜡速率的准确预测具有重要的指导意义。

1 基于改进天鹰优化器优化ENN模型构建

1.1 Elman神经网络模型构建

Elman神经网络模型是一种具有局部记忆单元和局部反馈连接的回归式网络[9]。不同于BP神经网络的是它在传统的三层网络结构基础上(输入层、隐含层、输出层),增加了关联层,因此具备记忆的特性。

其中,ENN模型非线性状态空间表达式为

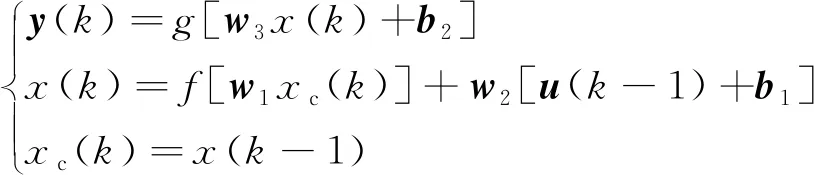
(1)

式(1)中:k为当前状态所处时刻;y(k)为输出节点单元的输出;x(k)为中间层的输出;xc(k)为关联层的输出;u为输入层单元向量;w1、w2、w3分别表示关联层与中间层的连接权矩阵、输入层与中间层的连接权矩阵、中间层与输出层的连接权矩阵;g() 、f()为输出层、中间层的神经元传递函数;b1、b2分别为输入层与中间层的阈值。

ENN模型在对权值与阈值进行更新时,实际上是采用误差反向传播和误差平方和函数进行衡量,其表示为

(2)

式(2)中:E(k)表示误差平方和函数;yd(k)为k时刻网络实际输出矩阵;y(k)为k时刻网络预测输出矩阵。

1.2 改进天鹰优化器的基本思路

1.2.1 鲸鱼优化算法狩猎策略的引入

鲸鱼优化算法(whale optimization algorithm, WOA)模仿座头鲸捕猎时主要分为两种策略:包围策略和狩猎策略[10]。改进天鹰优化器主要引进鲸鱼优化算法的狩猎策略,利用螺旋修正位置机制修正Xbest(t)和Xi(t)之间的距离,计算公式为

Xi(t+1)=D′eblcos(2πl)+Xbest(t)

(3)

式(3)中:D′表示当前搜索个体与当前最优解的距离;b为螺旋形状参数;l表示值域为[-1,1]均匀分布的随机数;Xbest(t)为当前最优解的位置向量。

1.2.2 改进天鹰优化器原理

天鹰优化器(AO)寻优过程分为四种方式:依据天鹰的飞行特性首先在高空翱翔选择搜索空间,然后通过短滑攻击的等高线飞行、滑翔在发散搜索空间内探索,最后通过低空飞行在收敛空间中探索猎物,并通过快速俯冲对猎物达到捕捉的目的[11-13]。文献[11]已给出天鹰优化器的详细原理,读者可自行查阅。天鹰优化器寻优过程中的四种数学表述为

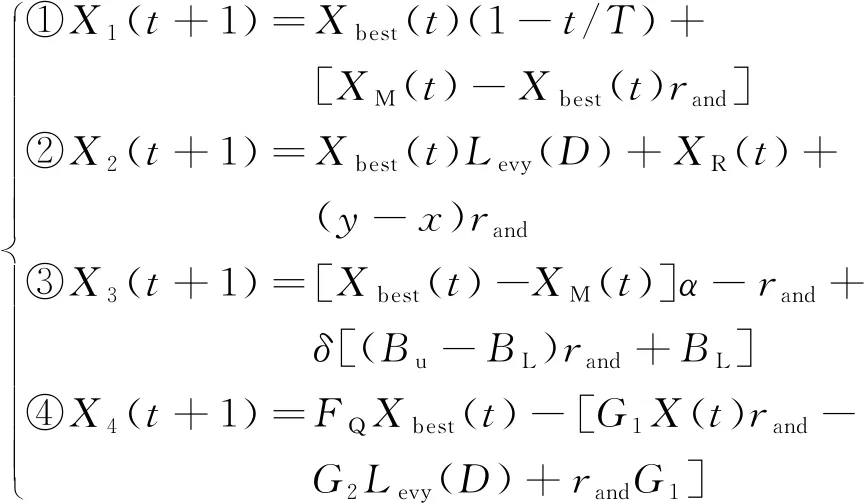
(4)

式(4)中:Xi(t+1)为天鹰使用方法i迭代的下一个解(i=1,2,3,4);Xbest(t)为当前最优解;BU、BL为搜索上、下界;t为当前迭代次数;T为最大迭代次数;rand为[0, 1]之间的随机数;XM(t)为当前解在t次迭代时的平均值;Levy(D)为惩罚飞行分布函数;XR(t)为t次迭代在[1,N](N为种群规模)范围内采用的随机解;y和x用于螺旋形状搜索;α和δ为调整系数取常数0.1;FQ为平衡搜索策略的函数;X(t)为迭代的当前解;G1为天鹰在捕捉猎物时的运动轨迹;G2为天鹰捕捉猎物时飞行首位置与末位置之间的斜率。

天鹰优化器作为新的群体智能优化算法,其和传统的优化算法都存在共同的缺陷,即:无法在全局和局部搜索之间获得最佳平衡,尤其是当其应用于高维数据集中的特征选择时。全局搜索与局部搜索不平衡则会导致收敛缓慢并很快陷入局部最优问题。改进天鹰优化器(IAO)是利用WOA的狩猎策略优势改进AO的一种耦合算法。具体而言,在IAO寻优过程中,WOA的狩猎策略被用作改进原始AO的局部搜索能力从而提高其解决不同优化问题的能力。

主要寻优过程为:首先使用天鹰优化器初始化全局参数并使用随机分布方法生成初始种群,进而使用目标函数[本文中使用预测样本的均方误差]衡量整体寻优过程中的最优解,然后利用AO全局搜索较好以及WOA局部搜索较好的优点对原始AO进行扩展开发[具体为使用鲸鱼优化算法原理狩猎策略式(3)对天鹰优化器寻优过程中的式(4)③进行替换]。因此,IAO在整个寻优过程中受益于天鹰优化器和鲸鱼优化算法的优势,通过改进后的四种方法对目标函数进行更新,将最优的结果(改进ENN模型的权值和阈值)保留至后续迭代,直到迭代达到停止条件,最终输出最优结果[14]。

2 基于改进天鹰优化器优化ENN模型的建模流程

传统ENN模型在预测管道蜡沉积速率时,存在泛化能力不足、易陷入极小点的缺陷,因此文中引入改进天鹰优化器对传统ENN模型的权值和阈值进行寻优处理。将每组天鹰的飞行位置(Xi)视为传统ENN模型的权值与阈值,通过目标函数本文使用预测样本的均方误差来判断天鹰飞行的最佳位置,迭代更新改进ENN模型的权值以及阈值,直至满足目标函数的最小精度或最大迭代次数时停止,其IAO-ENN模型流程如图1所示。

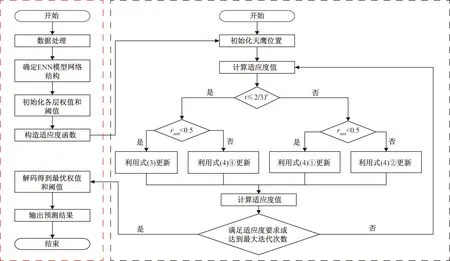
图1 IAO-ENN模型构建流程Fig.1 IAO-ENN model construction process

3 基于实测数据的改进新模型预测精度分析

3.1 数据选取与预处理

以文献[15-16]中给出的两组不同物性的原油管道蜡沉积速率实验数据为例(分别对应实例一、实例二),对比分析所建IAO-ENN模型和其他模型的预测精度。文献[15-16]中给出的原油管道蜡沉积速率实验数据分别为35组、38组,分别随机选取其中的30组数据作为训练样本建立模型,采用剩余的5组、8组数据(预测样本)来对比分析各模型的预测精度。具体的训练样本分别如表1和表2所示。

表1 原油管道蜡沉积速率训练样本[15](实例一)Table 1 Training samples of wax deposition rate in crude oil pipeline[15] (example 1)

表2 原油管道蜡沉积速率训练样本[16](实例二)Table 2 Training samples of wax deposition rate in crude oil pipeline[16] (example 2)

在对训练样本学习时,由于变量间的量纲不同,需要使用mapminmax函数对数据进行归一化处理,即把各变量的数据映射到[0,1]范围内。

3.2 仿真结果对比及误差原因分析

文中各模型的代码使用MATLAB软件自主编程实现,在AMD Ryzen7 4800U CPU @ 1.80 GHz,内存16.0 GB,windows 10操作系统电脑端参数条件下通过Matlab R2020a软件对所建各模型进行仿真求解。在对传统ENN模型构建时,设定训练样本的学习次数为1 000次,学习速率为0.01,训练目标最小误差为0.000 01,动量因子0.01,最小性能梯度为1×10-6。其中传统ENN模型针对实例一、实例二实测数据确定隐含层节点数H时,计算公式为

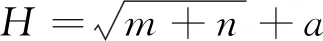
(5)

式(5)中:m表示输入层节点个数;n表示输出层节点个数;a取1～10的整数;H随a的改变而改变。

使用训练样本均方误差数值作为确定隐藏层节点个数的衡量标准,基于实例一、实例二不同隐藏层节点数求解的训练样本均方误差结果,如表3、表4所示。

表3 不同隐含层节点数计算训练样本的均方误差(实例一)Table 3 Calculation of mean square error of training samples with different number of hidden layer nodes (example 1)

表4 不同隐含层节点数计算训练样本的均方误差(实例二)Table 4 Calculation of mean square error of training samples with different number of hidden layer nodes (example 2)

由表3可见,当隐藏层节点数为11时,对应的训练样本均方误差最小(实例一),故实例一仿真试验确定构建7-11-1三层ENN模型。同样由表4可见,当隐藏层节点数为10时,对应的训练样本均方误差最小(实例二),故实例二仿真试验确定构建7-10-1三层ENN模型。

为了验证IAO-ENN模型的预测精度,文中建立了ENN、WOA-ENN、AO-ENN模型与其对比。为了便于分析,保持上述模型迭代寻优次数为50次,种群规模为30;其中WOA-ENN模型初始化常量取a=[0,2],b=1,l=[-1,1];AO-ENN、IAO-ENN模型初始化常量取α=0.1,δ=0.1。

仿真结束后,得到各模型管道蜡沉积速率的预测结果并计算相对误差,结果见表5、表6、图2以及图3。

表5 不同模型的预测结果及相对误差(实例一)

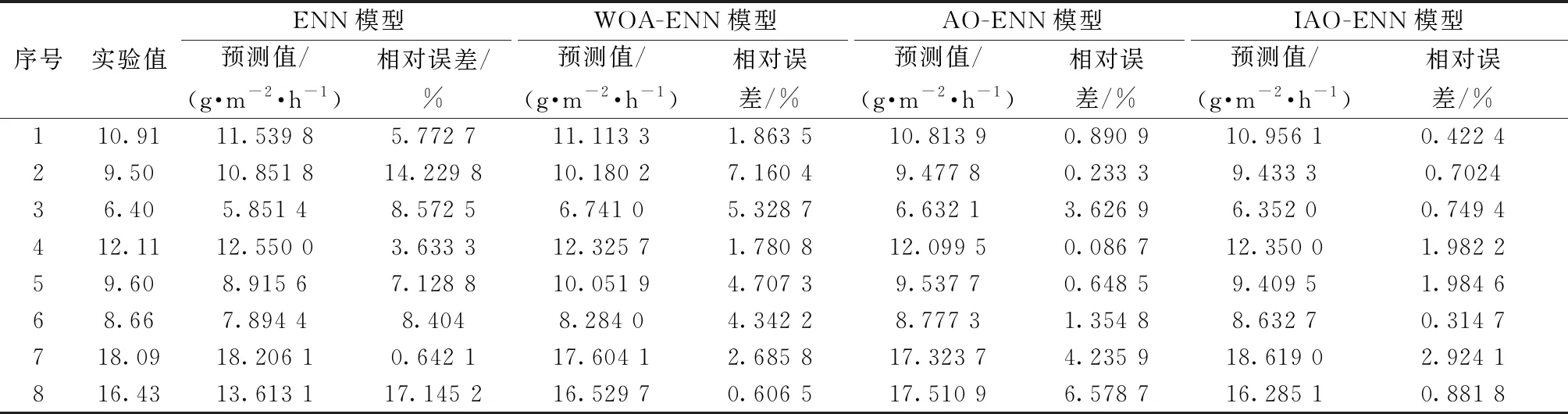
表6 不同模型的预测结果及相对误差(实例二)Table 6 Prediction results and relative errors of different models (example 2)

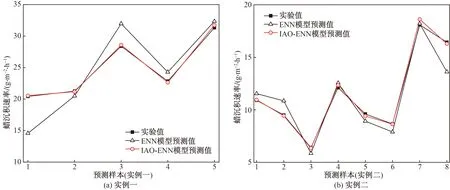
图2 不同实例IAO-ENN与ENN模型管道蜡沉积速率预测值对比Fig.2 Comparison of predicted values of wax deposition rate between IAO-ENN and ENN models in different examples

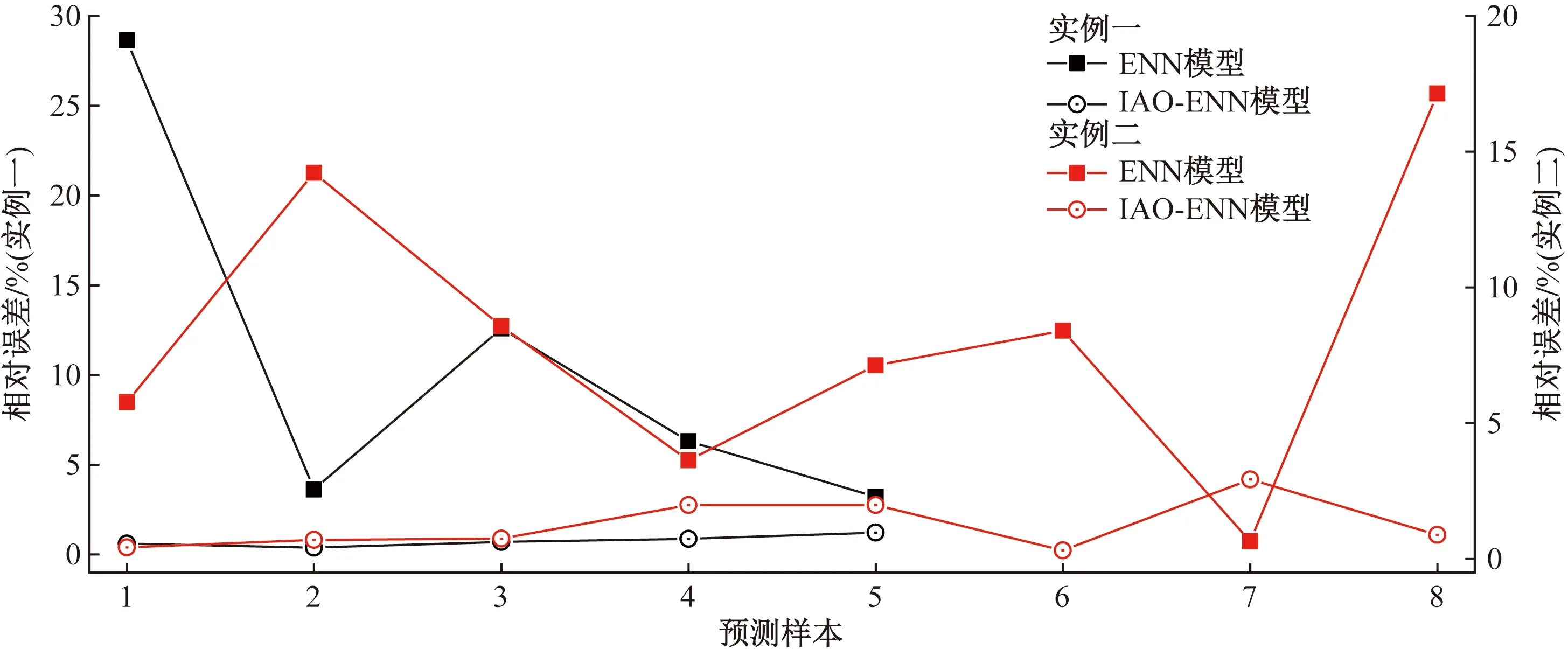
图3 不同实例IAO-ENN与ENN模型预测误差对比Fig.3 Comparison of prediction errors between IAO-ENN and ENN models in different examples

为评价各模型的预测精度,采用平均绝对百分比误差(mean absolute percentage error, MAPE)、均方根误差(root mean square error, RMSE)、相关系数R2对其进行评估,具体计算结果见表7。

表7 不同实例各模型预测精度对比Table 7 Comparison of prediction accuracy of different models in different examples

从表5～表7、图2以及图3可见,新建的IAO-ENN模型预测精度最高,其相关系数R2更接近1,且其平均绝对百分比误差分别仅为0.760 3%和1.245 2%。此外传统ENN模型的预测精度相对较低,WOA-ENN、AO-ENN模型的预测精度均高于传统ENN模型,这也证明了使用优化算法改进模型的有效性。

从以上预测结果可见,IAO-ENN改进模型可获得更高的预测精度,而传统ENN模型的预测精度较差。这是由于:对传统ENN模型而言,其Elmantrain函数应用误差反向传播训练函数对权值进行修正,这就导致梯度下降法求解E(k)对权值的偏导数时,存在易陷入局部极小点的缺陷。且传统Elman神经网络进行预测模型的创建时,初始的权值与阈值通常由伪随机数初始化产生,这就导致训练好的预测模型稳定性较差,进而导致泛化能力(机器学习对新样本的适应能力)不足[17-19]。

采用天鹰优化器建立改进ENN模型进行预测时,引入改进天鹰优化器可对初始化权值与阈值进行全局寻优处理,这就有利于:①尽可能克服了由初始权值与阈值取值不当,导致传统ENN模型在训练过程中使用梯度下降法对权值与阈值进行调整时,收敛速度过慢和易陷入局部极小点的缺陷;②避免了使用随机方式对权值与阈值进行赋值时,容易导致训练好的模型,针对其他样本预测时,较难取得精确预测结果的缺陷,提高了传统ENN模型的泛化能力。

此外新建的IAO-ENN模型较AO-ENN模型预测精度也有所提升,这主要是因为:新模型采用鲸鱼优化算法的狩猎策略改进天鹰优化器的捕猎能力,能够进一步提高原始天鹰优化器的局部搜索能力,故其预测精度较高。

从仿真结果可见,新建的IAO-ENN模型同样较WOA-ENN模型预测精度有所提升,这主要是因为:改进天鹰优化器将其寻优过程分为四种方式,既引进了鲸鱼优化算法局部搜索能力强的优势,又在迭代后期很好地平衡了全局搜索与局部搜索之间的关系,能够克服原始鲸鱼优化算法过早陷入局部最优解的缺陷,故其预测精度仍较高。

4 结论

(1)针对传统ENN模型的不足,在耦合鲸鱼优化算法与天鹰优化器的基础上,提出了一种基于改进天鹰优化器建立的改进ENN模型,并通过两个实例预测了原油管道的蜡沉积速率。结果表明,所建立的改进天鹰优化器优化ENN模型平均绝对百分比误差分别仅为0.760 3%和1.245 2%,其具有很好的预测精度。

(2)从改进天鹰优化器优化ENN模型和其他模型的对比结果可见,改进天鹰优化器优化ENN模型的拟合精度与预测精度均较好,传统ENN模型的拟合精度与预测精度最差。

(3)采用改进天鹰优化器优化ENN模型预测管道的蜡沉积速率完全可行,其有效解决了传统ENN模型预测时泛化能力不足、易陷入极小值的缺陷,该方法为结蜡速率的准确预测提供了新的途径,且拓宽了传统ENN模型的应用范围。