模型预测直接功率控制光伏储能双向DC-DC变换器研究
刘国宏
(中国石化胜利油田分公司 东辛采油厂,山东 东营 257000)
0 引 言
在能源产业中,太阳能光伏发电由于其发电材料来源广泛而占据极大比重[1],中国的阳光电源、科华数据等企业在光伏发电储能行业做出了卓越的贡献。太阳能光伏储能系统将太阳能转化为电能,进行能量的存储和电能变换。
光伏储能系统以蓄电池为储能结构,在分布式电源进行发电时,直流母线端经过双向DC-DC变换器给蓄电池端充电;当无光照等条件下需要蓄电池放电时,蓄电池端经过双向DC-DC变换器向直流母线端输送电能[2]。光伏储能系统中双向DC-DC变换器结构常见形式为非隔离半桥式双向DC-DC变换器,其良好的稳态性能和快速的动态响应性能是保证蓄电池长久工作和稳定的储能供能系统的必要条件。现阶段许多智能控制算法均应用在双向DC-DC变换器的性能控制中。文献[3-4]提出了一种模糊控制方式,实现了输出电压的超调抑制,减小了输出电流的纹波,但是模糊控制率难以整定,控制结构复杂;文献[5]针对传统PI控制器参数选择困难的缺点,提出模型预测控制(model predictive control, MPC)方法对三电平双向DC-DC变换器进行控制,实现了变换器性能的优化。
文献[6]为了解决氢燃料电池电动汽车双向DC-DC变换器动态响应不足和输出电流纹波大的问题,提出了一种带有约束项优化的MPC方法,优化了变换器的动态和稳态性能,但是在电流控制过程中优化项的权重选择难以确定;文献[7]建立电动汽车双向DC-DC交错并联结构的电感电流预测模型,提出了带有约束条件的价值函数,并利用粒子群算法求解价值函数最优解,使得系统具有更快的动态响应和更小的电感电流纹波,但是通过实验分析可知需要花费大量的计算来寻求粒子最优位置,增大了处理器的计算量。现阶段MPC以预测电流响应为主,且带有一定的约束条件,在此情况下对代价函数的寻优将会增大处理器的计算量,且求得的最优解可能不是全局最优解[8-9]。在储能系统双向DC-DC变换器中,可以直接对变换器输出功率进行预测,在改善变换器性能的同时避免了代价函数中权重的选择,同时也减少了处理器计算量。
该文建立变换器功率模型,分析光伏储能双向DC-DC变换器的功率模型预测控制过程,改善变换器的动态性能,避免代价函数以权重项的选择,减少处理器计算量。
1 电路工作原理
双向DC-DC电路如图1所示,图中:Vbat为蓄电池端电压;R为直流母线等效电阻,其端电压为Vbus;S1和S2为功率开关管;D1和D2为反并联二极管;C1和C2为输入和输出端滤波电容;L为功率电感,其电流为iL。双向DC-DC变换器正向工作在升压状态,蓄电池端向直流母线提供电能;反向工作在降压状态,直流母线通过双向DC-DC电路给蓄电池充电。

图1 双向DC-DC电路
以电感电流连续为例进行分析,在正向升压过程中,电路经历2个工作模式。正向工作过程中的驱动信号及电感电流波形如图2所示。

图2 正向工作波形
模式1中,S1导通且D2和S2关断,电感L储能,输出端电压由C2提供,电感电流增大,此阶段有
(1)
经过离散化后可得
(2)
式中:iL(k)为k时刻电感电流;iL(k+1)为k+1时刻电感电流;Vbat(k)为k时刻蓄电池端电压;Ts为采样周期。
模式2中,D2导通且S1和S2关断,电感L放能,电感电流减小,此时阶段有
(3)
对式(3)离散化后可得
(4)
式中:Vbus(k)为k时刻直流母线端电压。
正向过程断续情况下,共3个工作模式,前2个模式与连续情况式一致。模式3中,电感电流为零值,蓄电池端与直流母线端无关联,相互之间无功率的交换过程。
在反向降压过程中,电感电流连续工作下电路也经历2个工作模式,反向工作过程驱动信号及电感电流波形如图3所示。

图3 反向工作波形
模式1中,S2导通且D1和S1关断,电感L作为滤波原件,此阶段电感电流增大,有
(5)
离散化式(5)后可得
(6)
模式2中,D1导通续流且S1和S2关断,电感L的电流减小,此时阶段有
(7)
对式(7)进行离散化后可得
(8)
反向过程断续情况下,同样有3个工作模式,前2个模式与连续情况式一致。模式3中,电感电流为零值,蓄电池端与直流母线端无关联。假设开关管函数为
(9)
经过以上分析可知,功率开关管S1和S2对应00、01、11这3种开关状态,k+1的电感电流iL(k+1)能够通过k时刻的电感电流iL(k)、蓄电池端电压Vbat(k)和直流母线电压Vbus(k)预测得到。
2 模型预测功率控制
(10)
电容C2在k+1时刻的电流为
(11)
根据基尔霍夫电流定律则可知输出直流母线电流为
iR(k+1)=iL(k+1)+iC2(k+1)
(12)
因此可得正向工作过程中k+1时刻输出功率为
Pboost(k+1)=|Vbus(k+1)iR(k+1)|
(13)
目标输出功率为
(14)
可得以功率控制为目标时,升压过程代价函数为
(15)
(16)
电容C1在k+1时刻的电流为
(17)
因此可得反向工作过程中k+1时刻输出功率为
Pbuck(k+1)=|Vbat(k+1)ibat(k+1)|
(18)
式中:ibat(k+1)为k+1时刻蓄电池充电电流。
反向工作时功率控制代价函数为
(19)

提出的模型预测直接功率控制流程图如图4所示,求得代价函数最优解对应的开关管状态,实现输出功率控制。建立代价函数过程中,避免了电流优化过程中权重的抉择,只优化功率项,减少了处理器的计算量。

图4 模型预测功率控制流程图
3 仿真实验
为了验证提出的光伏储能双向DC-DC变换器功率模型预测控制策略具有优良的性能,在Matlab仿真软件中搭建仿真模型进行分析,仿真参数如表1所示。
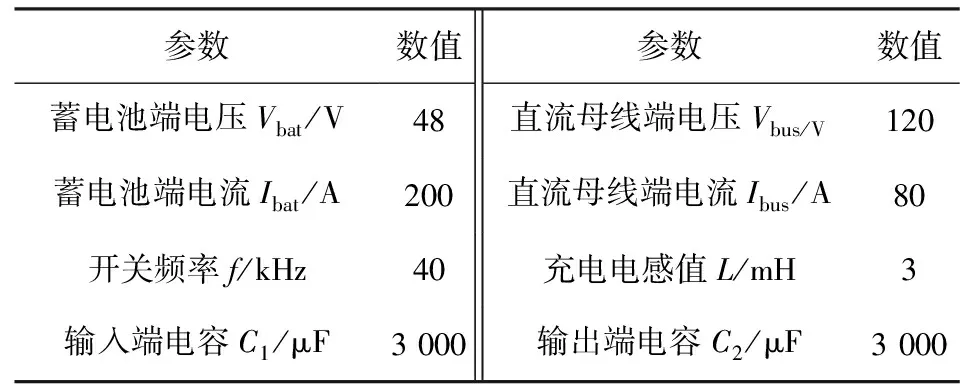
表1 仿真参数Table 1 Simulation parameters
根据表1参数进行仿真分析,直流母线端对蓄电池端供电时,电路工作在降压状态,仿真波形如图5 所示。启动之初蓄电池端指令参考电流为100 A,在0.1 s时蓄电池指令参考电流突变切换到200 A。启动过程中,提出的模型预测直接功率控制比传统PI控制具有更小的超调量;指令参考电流切换过程中,提出的控制方法也具有更快的响应,且不会出现正向超调。传统PI控制和提出的控制方法均能使降压电路得到稳定的输出直流静态误差小。

图5 降压过程工作波形
升压过程中,蓄电池端向直流母线端供电,提出的模型预测直接功率控制与传统PI控制电路仿真波形对比如图6所示。电路启动时直流母线端负载电阻值为3 Ω半载启动,提出的模型预测直接功率控制比传统PI控制具有更小的超调量,二者的静态误差均很小;在0.1 s时负载直接突变切换到1.5 Ω达到额定满载状态,提出的控制方法具有更快的响应,且正向超调更小,二者的输出直流静态误差均很小。

图6 升压过程工作波形
为了进一步验证提出的模型预测直接功率控制具有良好的性能,进行了样机实验验证,实验参数如表2所示。电路选择处理器为DSP数字处理器TMS320F28335。

表2 实验参数
正向升压过程中,动态切换实验波形如图7所示。

图7 升压动态实验波形对比
升压过程中电路满载启动,电路稳定后2种方法均能稳定到参考给定值,由满载向半载切换后,根据图7可知,提出的控制方法动态响应更迅速,具有更小的超调,二者均具有良好的稳态性能。
反向降压过程,动态实验波形如图8所示。提出的模型预测直接功率控制方法和传统PI控制方法稳态性能良好,均能在额定指令电流值一半处稳定工作;在指令参考电流一半向额定值切换过程中,提出的控制方法动态响应迅速,且无超调出现,传统PI控制方法出现超调且动态响应时间较长。

图8 降压动态实验波形对比
根据图7和图8可知,提出的模型预测直接功率控制方法与传统PI控制方法比较,二者均具有良好的稳态性能,但是提出的新方法能够使得双向DC-DC变换器具有更好的动态性能。
4 结 语
创新性地提出一种应用于光伏储能双向DC-DC变换器中的基于模型预测直接功率控制方法,以功率控制为目的,优化目标明确,避免了代价函数中多目标优化权重系数的选择,简化了处理器的计算量。仿真和实验结果表明,提出的方法相比于传统的PI控制方法具有更快的响应速度和更小的超调量,具有实际应用意义。

