SAPF的改进重复控制技术研究

甄景龙,杨逸帆,尹 晗,张莉卓

(1.深圳市正弦电气股份有限公司,广东 深圳 518014; 2.航天规划设计集团有限公司,北京100012;3.沈阳航天三菱汽车发动机制造有限公司,沈阳110179; 4.海信电子信息集团, 山东 青岛 266100)

0 引 言

并联有源滤波器(shunt active power filter,SPAF)能够有效补偿电网中非线性负载引入的谐波电流以及无功功率等问题。目前有源电力滤波器的电流跟踪技术已经被广泛应用[1-2]。

近几年重复控制器的改进策略被广泛关注。文献[3]提出采用PI+重复控制能够有效解决三相不平衡的问题,由于重复控制存在一个周期的采样延时,动态响应较慢,三相不平衡的补偿效果也会受到电网中谐波电压的影响。文献[4]提出基于傅里叶变换的重复控制器结果,将正反馈延时缩短为1/2,实现对特定次数谐波的无静差追踪,提高动态响应速度。文献[5]提出将重复控制内模中的延时缩短为原1/6,动态响应提高6倍,但由于存在非整数延时导致重复控制谐振峰与谐波之间存在相差。文献[6-7]分别提出针对电网次谐波的改进重复控制算法,通过重塑重复控制反馈通道和延时环节,提高重复控制器的动态响应和稳定性。文献[8]提出dq轴坐标系下存在有功电流和无功电流解耦,采用αβ坐标系简化解耦过程,并采用自适应内模结构。dq轴下LCL滤波器属于高阶模型,解耦复杂,不利于SAPF的控制。

该文采用基于正反馈结构的重复控制器,使重复控制器中引入零点,提高重复控制器带宽和增益。通过傅里叶变换得到重复控制器可以等效为比例控制器、积分控制器和无穷谐振控制器的叠加。采用准谐振设计的方法对重复控制的带宽进行等效设计,以实现对电网谐波的无静差追踪。对提出的改进重复控制模型进行理论推导和实验验证。

1 改进型重复控制器的结构及原理分析

改进型重复控制器与重复控制器均采用内模原理,不同的地方在于其反馈结构。2种基于内模结构的控制模块的原理框图如图1所示[9]。图1中K为延时衰减系数,Td为重复控制的周期,E(s)为控制系统的输入误差,Y(s)为重复控制器输出。

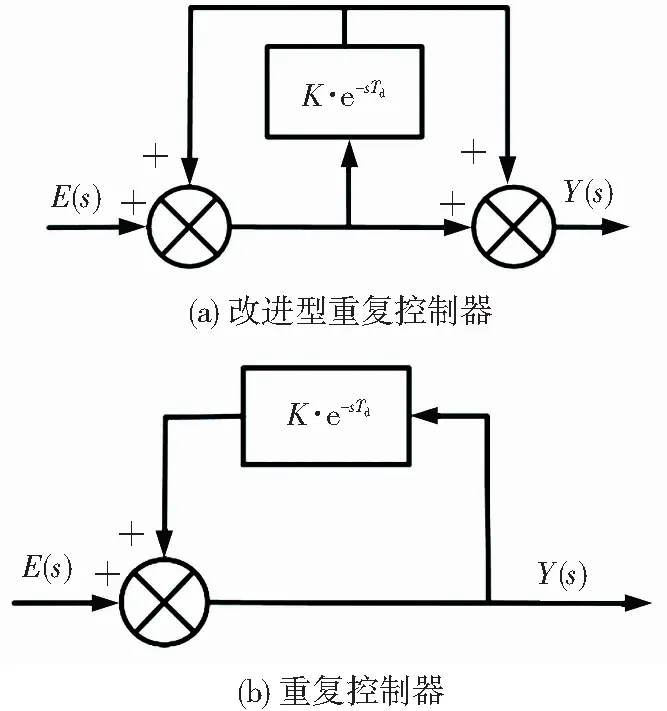
图1 2种内模结构控制器原理图

从图1的2种控制器的原理框图可以看出,改进型重复控制器相较重复控制器增加1个正前馈环节,其特点及优势将通过数学分析进行说明。从图1所示的2种控制器结构框图,可以得到2种重复控制器的输入-输出传递函数。

重复控制器:

(1)

改进型重复控制器:

(2)

从式(1)、式(2)可以看出,当K=1时,改进型重复控制器在零极点的配置上与重复控制器有差异,如图2(b)所示为重复控制器全部为极点,而图2(a)所示为改进型重复控制器中部分极点变成零点。

图2 2种内模结构控制器零极点分布

如图2(a)所示改进型重复控制器引入正前馈的环节,引入零点。图3在相同的增益K之下[10],可以通过2种控制器的幅频响应得到其性能的对比。改进型重复控制器中引入零点导致系统的稳定性能提高,允许系统在谐振频率处有更高的增益,且其谐振峰处的带宽要明显优于重复控制器。

图3 2种内模结构控制器幅频响应

将延时衰减系数K改写成指数形式:

K=eσTd

(3)

式中:σ为指数衰减系数。

(4)

由文献[11]可以得到

(5)

式中:n为谐波次数。

(6)

从式(6)可以看出,改进型重复控制器可以展开成一个积分项和一组谐振器的结合,可以补偿所有基波整数倍的各次谐波,且谐振器的增益受σ影响,即由延时衰减系数K决定。

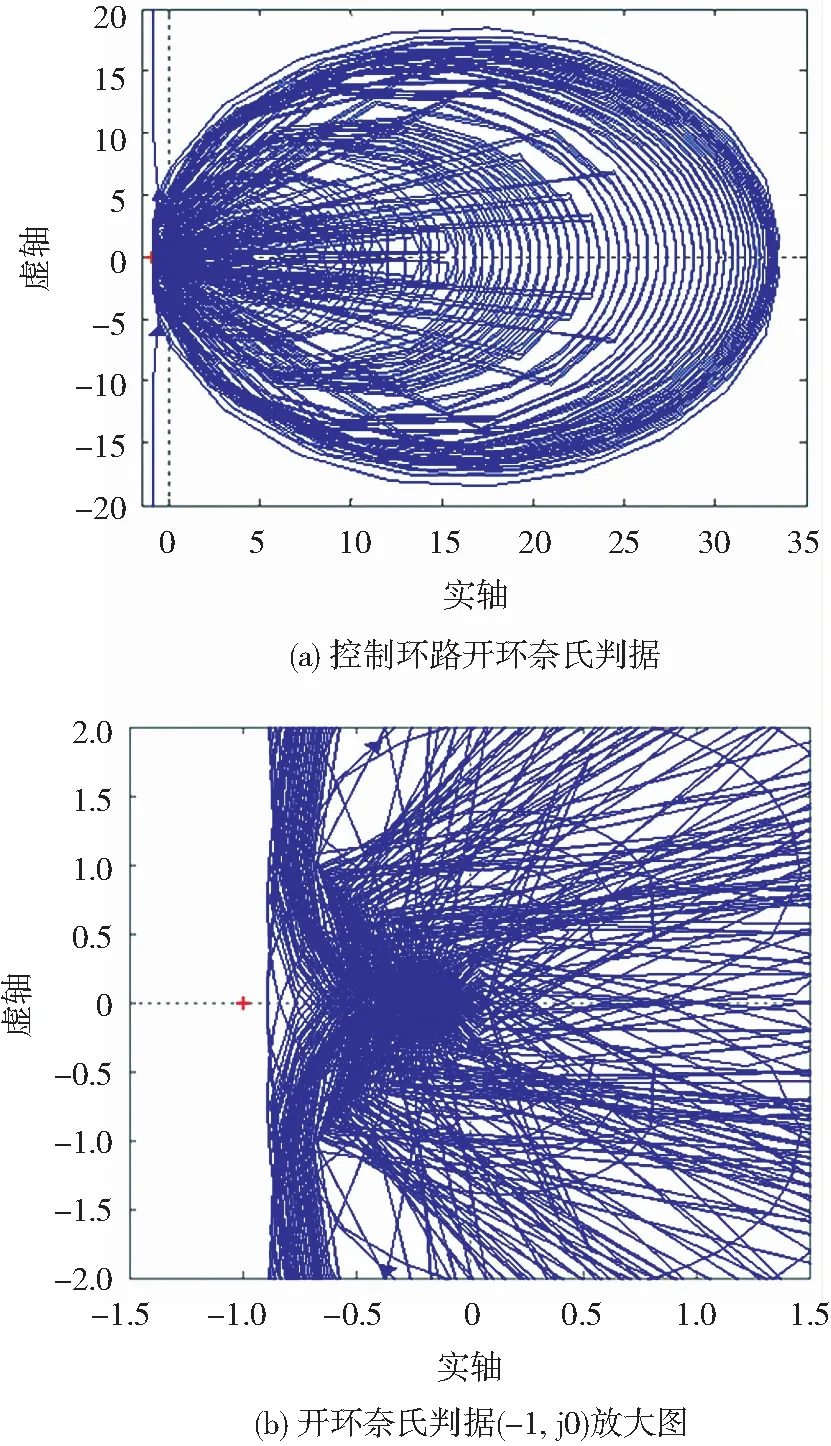
当K=1时,即σ=0。这时谐振器为理想谐振器,在谐振频率处有无穷增益[13]。但在实际应用中,会引起系统不稳定,需要添加阻尼系数,即需满足0

(7)

式中:Kr为谐振器增益;ωcut为剪切频率;ωh为谐振频率。

对比式(6)和式(7),可以发现求和公式中每一项都可以近似为谐振公式。式中,由于σ取值很小,在分子中的σ和分母中σ2产生的影响可以忽略不计。σ的主要作用是产生阻尼,并且式(6)中第一项为一阶积分项,在计算谐振频率时不产生影响,则式(6)可以近似为[11]

(8)

从式(8)中可以看出,谐振器的带宽将由σ决定。将s=jω代入式(8)中,可以得到频域计算式:

(9)

|Gc(jω)|=Kw

(10)

可得

(11)

根据国家标准要求,电力系统的频率偏差为电力系统正常运行条件下频率偏差限值±0.2 Hz。按照±0.2 Hz进行设计,则要求式(12)中满足

|ω-nω0|≥2π×0.2

(12)

可以解得σ≥1.259 2,即K≤0.975 1,此时Kw=68.89,即改进型重复控制器的增益为38 dB。

为了使系统具有良好的鲁棒性,适当放宽带宽,取K=0.97,改进型重复控制器的增益为36.3 dB。这时改进型重复控制器的传递函数为

(13)

2 基于改进型重复控制器的控制系统设计

考虑电流跟踪控制器需要满足稳态精度和动态响应,采用比例控制与改进型重复控制器的复合控制结构。2种控制的组合方式为并联方式,其优势在于,可以将较复杂的控制环路设计拆分成2个较简单的设计。一方面在不考虑改进型重复控制器的情况下,单独考虑比例环节时系统的稳定性设计;另一方面,在比例环节下系统稳定,那么只需要改进型重复控制器自身是稳定的,则能保证整个系统的稳定性。

同时采用电网电压前馈的环路,可以提高控制系统对电网电压的扰动影响,在实际中可以降低设备启动电流,提高设备运行的稳定性。最终确定所采用的控制器结构如图4所示。在图中可以发现,改进型重复控制器环节包括三部分:改进型重复控制器部分Gc(z)、周期延时部分K2z-N、补偿结构部分C(z)zd。比例控制环节包含比例函数Gp(s)和陷波器函数Gtrap(s)。

图4 控制器结构示意图

由于需要构成内模信号,引入周期延时K2z-N,同时补偿结构部分,由于无相移滤波器的加入引入延时量,也需添加超前量zd进行补偿。因此,需要对该部分的加入进行控制器的稳定性分析。

为方便分析,周期延时的z-N的s域形式为e-sT,写成频域形式,则可得

e-jωT0=cos(-ωT0)+jsin(-ωT0)

(14)

可以得到其相位角φ与角频率的关系为

(15)

从式(15)可以得出,延时环节e-sT0的相角φ与频率之间的关系是线性关系。改进型重复控制器本身是稳定的,但是加上延时环节后,构成的传递函数Gc(z)K2z-N会反复穿越-(2k-1)π。

在频域范围内,当|Gc(jω)K2e-jωT0|=0 dB时,可以解得,其对应的相位角小于-180°,即系统是不稳定系统,需要对传递函数Gc(z)K2z-N进行修正。

这里设计比例系数K2来增加函数的相位裕量。由图3可以得知,在谐振峰频率前后,改进型重复控制器相频特性都会发生跳变,跳变前后的相角均近似为90°,为增加相位裕量,设计新的相位特性跳变为|90°-β|,其中β为一较小角度,则当幅频增益为零时,即|Gc(jω)K2e-jωT0|=0 dB,传递函数的相位随频率变化的关系为

(16)

由于控制器阶数太高,解析解获取过于复杂,这里对图5观察得知,改进型重复控制器相位关于谐振频率对称,当k=1,2时,则有

图5 K2取值0.51时传递函数稳定裕量

(17)

其中β为裕量值,判断系统是否稳定可由当传递函数增益为零时,相移小于180°,或相移为180°时,传递函数增益小于零进行判断。当相移为180°,则有

(18)

解得ω=0.75ω0、1.25ω0,在每个频段范围内,可以将系统看作为最小相位系统,其相角随着频率单调变化,代入|Gc(jω)K2e-jωT0|<0 dB,可以得到K2的取值范围为

(19)

根据式(19),在一次谐振器即50 Hz处,要求的相位裕量条件下,可以解出K2的取值范围为0

被控对象传递函数为GLCL(s),不考虑电网电压前馈的情况下,对于改进型重复控制器环路而言,改进型重复控制器的开环传递函数为[16]

Gop(z)=Gc(z)K2z-N+dC(z)GLCL(z)

(20)

采用Nyquist判据来判断式(20)的环路稳定性[17]。系统开环Nyquist判定如图6(b)所示。

图6 改进型重复控制器开环Nyquist图

对于比例环节的设计,比例环节主要负责系统响应速度。由于不能有延时环节,因此其补偿环节不能采用无相移陷波器,这里采用普通二阶陷波器进行设计。陷波器的函数为

(21)

式中:ωres为陷波器的陷波频率,这里设计其等于LCL型滤波器的谐振频率,以加强对谐振峰的抑制;Q为陷波器的品质因数,品质因数越小,则陷波器带宽越大,相移也越大。选择Q=0.5,ωres=3 751·2π rad/s,则陷波器幅频响应如图7所示。

图7 陷波器的幅频响应

比例环节的比例系数越大,则带宽越宽,系统响应速度越快,但系统稳定裕量降低。比例系数越小,系统稳定裕量越高,但系统的带宽越低,系统的响应速度越慢。因此,需要在系统稳定性和响应速度之间做出权衡,已知系统的比例开环传递函数为Gp(s)、Gtrap(s)、GLCL(s),这里通过对该函数进行如图8所示的伯德图分析可得在不同的比例系数下,系统的幅频响应和稳定裕量。

图8 不同比例系数比例环节的开环幅频响应

选择比例系数为10,从图8可见,比例环节的闭环稳定,且增益裕量为16.4 dB,相位裕量为71.2°。整个控制环路的传递函数为

G(s)ol=[Gp(s)Gtrap(s)+

Gc(z)C(z)z-N+d]·GLCL(s)

(22)

对式(22)进行Nyquist判断,可以得到图9。

图9 控制环路的开环Nyquist图

由控制环路的开环Nyquist图可以得到,其未包围(-1,j0)点,则闭环系统为稳定系统,验证了所设计的控制环路的有效性。

3 仿真及试验结果分析

3.1 仿真结果及分析

在Matlab的SimPowerSystems中搭建三电平有源电力滤波器仿真模型,负载由三相不控整流桥及阻容负载组成[18]。根据图4所示的控制系统框图整定系统参数,根据第2节的分析,设计的有源滤波器硬件参数与控制参数[19-20]见表1、表2。

表1 有源滤波器的硬件参数

表2 有源滤波器控制参数Table 2 Control parameters of SAPF

如图10(b)所示,非线性负载中谐波主要成分为5次、7次、11次、13次、17次,其中5次和7次的谐波含量最高,总谐波畸变率(total narmonic distortion, THD)值分别为24%和6.52%。非线性负载总的THD值为25.95%,基波有效值为13.82 A。

图10 负载电流补偿前的仿真分析

如图11(a)所示,采用提出的改进型重复控制器后电流的正弦度明显提高,如图11(b)所示,电流总THD值下降为2.09%。其中5次、7次谐波得到有效补偿。

图11 补偿后的电流仿真分析

3.2 试验结果及分析

在仿真试验基础上进行试验验证,试验参数如表1所示。设计1台2 kVA小型有源电力滤波器,最终搭建试验平台对该文所提改进重复控制算法进行验证。

图12为试验设备整体原理图,采用DSP28335和DSP2812双控制器系统,实现谐波电流检测、电流补偿算法、直流电压控制以及PWM法波算法等功能。LCL滤波器将输出PWM电压转化为谐波电流。图13所示为该文设计的有源滤波器硬件试验装置图。

图12 试验设备整体原理图

图13 试验设备外观图

图14(a)为设备正常工作时,上位机观测到补偿前电网电压和电流波形,A相电流波形存在严重的畸变。如图14(b)所示,通过上位机中FFT分析可得A相电流的谐波的THD值为29.49%。其中5次、7次、9次等谐波含量较高,远高于国家标准的5%。

图14 A相谐波电流和谐波频谱分析

图15(a)所示为补偿后通过示波器观测A相电压和电流,补偿后电网电压和电流相位基本一致,且正弦度较高。图15(b)所示为补偿后的A相电流谐波频谱,补偿后A相电网电流的THD值为2.79%。

图15 补偿后A相电流和频谱

4 结 语

针对基本重复控制使用过程中易出现不稳定的问题,提出基于正反馈的改进重复控制策略。由于零点的引入,控制器的带宽和补偿增益得到显著提高,仿真和试验结果表明,改进重复控制能够有效补偿谐波。

重复控制器的设计十分复杂,对处理器的内存和响应速度较高。同时还存在一个周期的误差延时,不适用于动态响应较快的场合。建议在误差要求较高并且动态响应不高的场合应用。