雷电冲击电压下空心电抗器电压分布特性研究

申昱博,张 健,陈莉娟,刘 骥,刘贺千,张明泽,朱东柏

(1.国网黑龙江省电力有限公司电力科学研究院,哈尔滨 150030; 2.国网太仓市供电公司,江苏 苏州 215400;3.哈尔滨理工大学工程电介质及其应用教育部重点实验室,哈尔滨 150080)

0 引 言

电抗器作为一种重要的电力设备,在电力系统中起补偿杂散容性电流、限制合闸涌流、限制短路电流以及对电路和设备进行滤波、平波、启动、防雷、阻波等作用[1-3]。在空心电抗器的实际运行过程中,不但要遭受到工频过电压的冲击作用,同时也要承受来自雷电过电压的冲击作用[4-5]。雷电冲击过电压可以在短时间内迅速上升到其电压峰值,从雷电压的电压波形可以看出,在波前时间内,电压波形十分陡峭,几乎呈直线升高。当雷电过电压作用在电抗器时,电抗器需要在短时间内承受幅值极高的电压[6],这不仅会对电力电抗器的绝缘结构造成损害,也严重危害电网的稳定运行。

空心电抗器在冲击过电压的作用下,线圈之间会产生电磁感应,线圈内部发生振荡过程[7],对该过程的分析不仅可以得到雷电压冲击下电抗器线圈绕组上的电压初始分布情况,还可以计算出各绕组匝间电压差,以此可在设计和制造过程中为选择绝缘厚度、气道厚度等参数提供参考数据,从而设计出满足绝缘裕度要求的最优电抗器绝缘结构。

由于不同电压等级的空心电抗器包封数量不同,且各包封内的线圈并联匝数较多,存在并绕情况,使用仿真软件对其建模后的计算结果与实际经验值相差巨大,无法有效获取电压分布参数。因此通过有效的数值计算手段,准确快速地获得电抗器在雷电压冲击下的电压分布特性,具有重要的工程意义。

1 高频下空心电抗器等效电路模型

在传统的空心电抗器低频模型中,电抗器只是被等效成电感,这种模型无法有效描述电抗器高频特性。而在雷击电压作用下,电压作用时间为微秒级,电抗器内多匝线圈中的电容、电阻特性均不能忽略。

1.1 初始暂态过电压下的电抗器等值电路

高频等效电路模型中含有电感与互感的支路中,存在自感抗值与互感抗值为无限大的情况,此时相当于断路状态。在直角波波头作用时,将电抗器等值网络简化成如图1所示的复杂电容电路网络模型,该电路模型仅由电容组成。

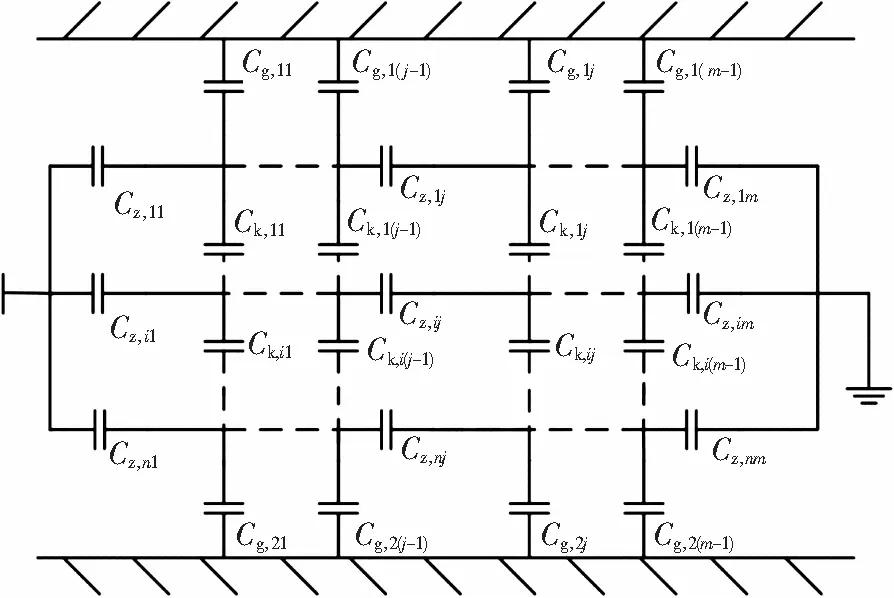
图1 初始电抗器电容网络等值模型

设定电抗器的线圈层数为n,每层分为m份。其中,Cz,ij代表第i层第j段匝间电容,每层线圈绝缘导线规格相同,各段匝电容相等;Ck,ij代表第i层第j段与第i+1层第j段之间沿轴向的层间电容,两层线圈间绝缘结构相同,在包封内部为环氧玻璃丝绝缘,包封间为气道,各段线圈层间电容也相同;Cg,1j与Cg,2j分别代表电抗器内外径的两个表面沿轴向的对地分布电容。

1.2 稳态电压下的电抗器等值电路

在雷电压波波尾时,其电抗器高频等值模型应考虑线圈间自感、互感及电阻的影响,电抗器的阻容网络等效电路如图2所示。分布电容参数与图1相同;Lij代表第i层支路的第j段的自感及第i层支路的第j段与n-1个线圈的互感之和;Rij代表第i个线圈第j段的交流电阻,交流电阻包括导体电阻和含涡流损耗的等值电阻。

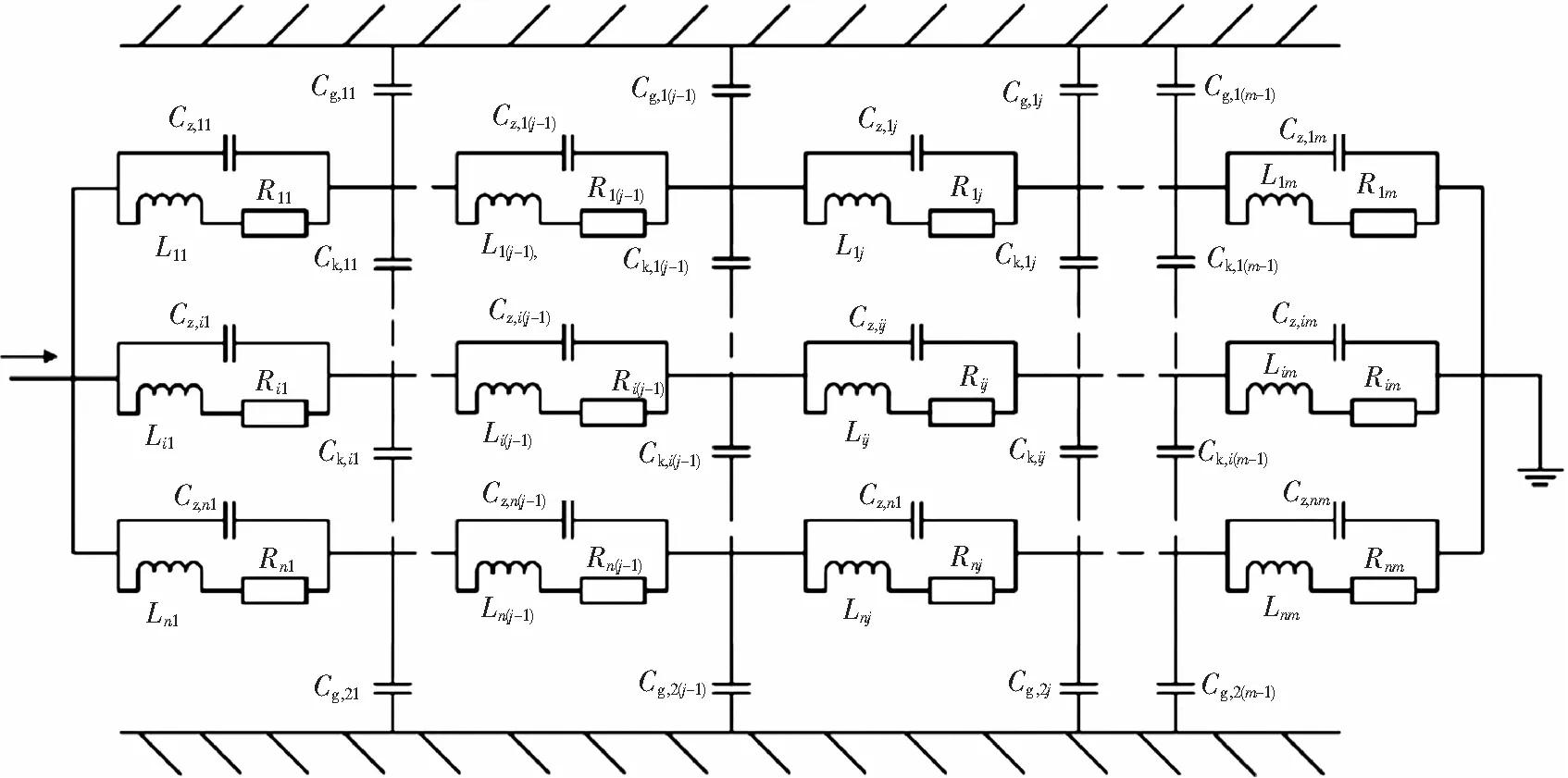
图2 稳态电抗器阻容网络等值模型

2 等效模型参数计算

电抗器等值模型中,参数确定对其雷电压下的电位分布计算十分重要。实际的电抗器结构,自感、互感分布已明确,但在高频作用下其电容网络与电阻网络却十分复杂,该文将对高频激励下两种参数的等值计算方法进行分析。

2.1 等值电阻网络构建

高频下空心电抗器的电阻分析既要考虑导体电阻,同时也要考虑集肤效应交流电阻值的影响,以及涡流损耗的等值电阻。

1)导体电阻:空心电抗器各线圈都是通过铝导线绕制而成,导体电阻值的大小与导体材料、几何尺寸相关。

第i层线圈的导体电阻可表示为

(1)

式中:ρ0为0 ℃时导体的电阻率;T为电抗器的工作环境温度;α为该导体金属材料的温度系数;di为导线直径;ri为第i层线圈的内径;hi为第i层单匝导线高度;ni为第i层并联匝数。

2)集肤效应电阻:当交变电流流过导线时,导线的等效电阻值不再是导线的直流电阻值。

根据麦克斯韦微分方程及电流密度与电场强度、磁场强度与磁通密度之间的关系,单位长度的交流电阻(复阻抗实部)表达式为

(2)

式中:k为涡流系数,与导体的电导率及磁导率有关;γ为导体电导率,铝的电导率[1]为3.7×107S/m;δ为集肤深度,与激励的角频率、导体的电导率及磁导率有关;r为导线截面半径值;ber(kr)、bei(kr)为零阶开尔文函数,ber′(kr)、bei′(kr)为一阶开尔文函数。

当导线中通过高频电流时,导线截面半径r远大于此时的集肤深度,此时式(2)进一步可计算得到:

(3)

式中:Rdc表示直流电阻,Ω。

3)涡流损耗等效电阻:空心电抗器的结构形式一般采用多包封,多绕组并联,许多细导线相互并联绕制而成每层绕组。以圆导线为例,导线圆环上回路单位长度dx的电阻为

(4)

于是可得单位长度dx回路产生的涡流损耗为

(5)

因此可得等效损耗:

(6)

式中:f为电源频率;a为圆导线截面积;ρ为导体电阻率;Bi为导线的磁感应强度;l为导线长度。

由式(6)可知,涡流损耗与磁感应强度的平方、电源频率及其垂直入射的面积成正比,根据Bartkey变换方法可获得整个电抗器对空间任意处的磁场强度及等效电阻值。

2.2 等值电容网络构建

1)匝间电容:电抗器的匝间电容由两部分组成,两相邻线匝之间的分布电容如图3所示。

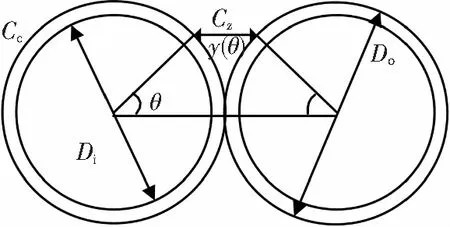
图3 相邻线匝间电容

由图3可知,邻近匝间电容是通过导线1、2表面绝缘层电容Cc、匝间绝缘电容Cz三部分串联形成,匝间总电容Ct可以表示为

(7)

式中:ε0为真空介电常数,8.854×10-12F/m;εr为绝缘的相对介电常数;lt为单匝线长度;Do为导线外径;Di为导线内金属外径。

2)层间电容:电抗器是由多层同轴线圈相互并联构成,可以认为是同心圆柱模型,单匝导线高度层间电容Cp计算如下:

(8)

式中:d为铝导线直径;D1为内包封外表层直径;D2为外包封内表层直径;εr为绝缘的相对介电常数;h为单匝导线高度;n为单层并联匝数。

3)对地杂散电容:最外层的对地杂散电容就是由空气绝缘部分决定的电容,可以采用模拟电荷法进行计算,如图4所示。

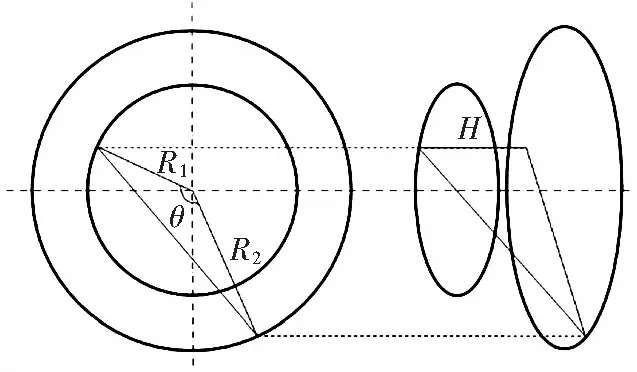
图4 带电圆环示意图

其中圆环电场可得到带有电荷量q半径为R1的圆环,在距轴向H半径R2位置的参考电位为

(9)

多匝导线时,导体上的电位与电荷量之间满足:

(10)

式中:Cnn为第n匝线圈对第n个参考点产生的等效电容;Un与φn表示相同的含义,为第n匝线圈参考点的电位。

3 算法实现与实例分析

3.1 雷电波入射时电压分布计算方法

根据上文中电抗器电阻分布网络及电容分布网络的获取,可得到电抗器整体的等值阻抗分布模型,初始暂态电压下单节点处电容分布模型如图5所示。

图5 暂态电压下电抗器电容单元电路

电压分布方程可表示为

(11)

同理,在雷电压波尾时间下单节点处阻抗分布模型如图6所示。该单元电路中包含支路电阻,匝间电容,对地杂散电容以及电路的自感与互感。

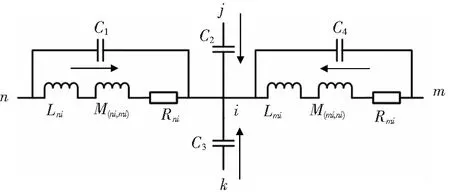
图6 稳态电压下电抗器阻抗单元电路

可获得电压分布方程:

(12)

式中:上角标s为迭代次数;M(mi,ni)、M(ni,mi)为两匝线圈间的互感。

设定雷击电压作用前,电抗器内部各节点处的电压初值为0,逐次通过式(11)、式(12)进行循环迭代计算,可得出电抗器内部各包封内各层线圈节点处的电压变化规律。

3.2 雷电波入射时电压分布计算实例

为验证该文计算方法的有效性,进行了电抗器雷电过电压下包封内电压分布的实际测试及计算。试验中采用的并联空心电抗器有18个包封,通过分压器采集电压波形,调整高压发生器的波头与波尾电阻,获得标准的雷电压电压波形。将分压器接到试验电抗器最外层的预留测量点上,测试不同匝间位置处的实际电压波形,试验电抗器现场接线如图7所示。

图7 空心电抗器雷击电压试验

通过现场试验得到空心电抗器标准雷电冲击电压下的电压分布情况如图8所示。

图8 电压分布实测波形

从试验得到的电压分布波形中可知,各支路电压都在振荡过程中趋于稳定。进一步比较匝间电压差的数值变化规律可知,匝间压差以振荡的形式逐渐减小,匝间压差的最大值出现在起始时刻位置。中上部匝间压差减小的速度相对较快,电压波形幅值随时间变化减小较为明显,而最下部匝间电压差值减小的速度相对缓慢,电压波形幅值降低相对较少,电压分布较均匀。

根据实际测试结果,最外侧包封三种不同位置的电压分布的不均匀系数分别为:最上层匝间不均匀系数为1.65,中层匝间不均匀系数为1.3,最下层匝间不均匀系数为1.15。为进一步计算并明确电抗器各包封匝间电压分布情况,采用提出的电压分布仿真计算方法对电抗器不同包封的匝间电压进行计算。

仿真计算采用Fortran语言,仿真计算中电抗器每个包封的轴向设置点数为40,包封绝缘厚度为2.5 mm,匝绝缘厚度为0.5 mm,气道厚度为25 mm,电抗器底端的对地高度为2.0 m,对于雷击电压下电抗器内部的电压分布,最外层包封中各节点承担的电压最大,因此在仿真计算中仅需考虑最外侧2个包封中的各层线圈电压分布即可,计算时间为30 μs。

根据计算发现第一个包封第1层线匝,仿真计算时间为1.2 μs时,最大压差较大,为51.94 kV;不均匀系数值也比较大,为1.67。随着对地高度的降低,各节点电压逐渐减小,减小的速度也越来越缓。当仿真计算20 μs时,最大压差为40.65 kV,此时的不均匀系数为1.63,匝间电压减小;同时为对比试验数据,对第一个包封中间第15节点及35节点进行计算(仿真计算时单个包封沿高度方向设定了35个节点,第15个节点为电抗器中间层线匝,第35个节点为电抗器最下层线匝),其不均匀系数分别为1.32及1.16,与实测结果1.3和1.15基本一致。仿真计算时对各包封中的电压均进行了计算,具体计算结果如表1所示。

表1 各包封最大电压差仿真计算结果Table 1 Simulation calculation results of maximum voltage difference of each sealing

由表1的仿真计算结果显示,最大电压差值均出现在电抗器最上端各支路的第1,2节点位置处,并且越靠近内外2个包封,电压分布不均匀系数越大,这一结果与实际测试结果基本一致。根据分析可知,在最内及最外侧包封均存在与大地间的对地电容(对地杂散电容),使电抗器各包封在暂态电压下的电压分布更不均匀,可见空心电抗器的绝缘压力主要由最外层和最内层包封承担,因此对于厂家进行电抗器设计时,应加强电抗器端部差异化匝间绝缘设计,以提高在冲击电压及暂态过电压下匝间绝缘能力。

4 结 语

通过对空心电抗器在高频电压作用下等值阻抗模型进行分析,分别建立了初始暂态电容分布模型及稳态阻抗分布模型,并提出了相应的节点电压的迭代计算方法,实现雷击电压作用下电抗器内部各层线圈的电压分布计算,主要结论如下。

1)电抗器线圈匝间电容计算时需考虑线匝间相邻角内绝缘对匝间电容的影响;对地杂散电容可通过计算电抗器外空气绝缘部分的对地杂散电容来表示。

2)受集肤效应的影响,交流电阻值增大,并且在高频情况下其增大现象更明显,交流电阻值远大于直流电阻值。

3)初始电压分布不均匀系数大于稳定时电压分布,且随着对地高度的增加电压分布不均现象更严重,最大电压差发生在电抗器包封首端匝间。

4)空心电抗器最内层和最外层的匝间压差和不均匀系数较大,其余部分相对较小。

采用提出的雷电压下电抗器内部电压分布计算方法,可有效计算不同容量、不同类型空心电抗器在雷击电压下出现的电压最大位置及冲击电压不均匀系数,并可根据其不均匀系数及雷电压可能出现的最大幅值,评估匝间绝缘的可靠性,为厂家对电抗器结构的优化设计及绝缘裕度的考量提供了一定的理论依据。