船舶压载水系统可靠性分析

杨 咏，王 晓，兑红炎，陶俊勇

(1. 船舶与海洋工程特种装备和动力系统国家工程研究中心(中国船舶集团第七〇四研究所)上海 200031；2. 郑州大学 管理学院，河南 郑州 450001；3. 国防科技大学 智能科学学院 装备综合保障技术重点实验室，湖南 长沙 410073)

0 引 言

船舶在海面航行时，会遇到各种不同的水域，需要调整船舶的浮力，船舶的压载水系统能够调整船舶的排水量[1]。船舶的压载水系统由多种不同的阀门、水泵组成，结构复杂，各组件分布船舶的不同区域，故障排查困难。由于船舶在航行的过程中所处环境复杂，压载水系统需要进行不停的压载、卸载工作，频繁的操作会降低各组件的可靠性。

船舶的压载水系统结构复杂，通过对船舶压载水系统的可靠性分析，能够帮助了解压载水系统的故障原因，更快地进行维修。张迪等[2]利用模糊集合论建立故障树，并对压载水系统进行可靠性分析及优化。李佩昌等[3]提出了模糊动态故障树分析方法，对船舶系统可靠性进行分析。白旭等[4]提出将系统故障树转化为贝叶斯网络，考虑节点的正常、一般故障、严重故障3 种状态，进行计算系统可靠度。易静[5]引入贝叶斯网络对系统可靠性进行分析。苏艳琴等[6]引入粗糙集和贝叶斯网络，对系统故障进行分析。姚成玉等[7]提出一种新型连续时间贝叶斯网络分析方法，计算子节点的故障概率。Mamdikar 等[8]提出了一个使用故障树和动态贝叶斯网络的动态可靠性评估框架。王晓明等[9]采用基于连续时间贝叶斯网络的建模及分析方法对系统的动态特性进行可靠性分析。Codetta-Raiteri 等[10]采用广义的连续贝叶斯网络对系统进行可靠性分析。张大信等[11]分析了4 种动态故障树顶事件概率的计算方法。Lei 等[12]利用动态故障树对不同的系统进行可靠性建模。

上述研究并没有考虑分析船舶压载水系统随时间变化的系统可靠性，并且基于连续贝斯网络的系统可靠性分析的研究较少。本文利用动态故障树分析了船舶压载水系统故障原因，基于现有的连续贝叶斯网络可靠性分析方法，将动态故障树转化为连续贝叶斯网络，分析系统的可靠性以及剩余寿命。

1 船舶压载水系统故障分析

船舶压载水系统能够保证船舶在海上运行过程中保持稳定。压载水系统结构复杂，设备众多，因此故障原因众多，故障分析困难[12]。图1 所示为简化后船舶压载水系统的组件结构图[13]。

图1 船舶压载水系统结构图Fig. 1 Structure drawing of ship ballast water system

图中，V1 和V2 等分别代表止水阀，P1 和P2 代表压载水泵，SP1 代表扫舱泵。可以看出，压载水系统包括压载水泵、阀门、扫舱泵，管道等。压载水的调驳包括压载和卸载两个过程。

压载即为系统吸水，压载的流程为打开海底门，1 号压载水泵工作，海水通过1，2，3 号阀门，进入AZ（压载水处理装置）进行海水的净化。海水净化后，依次通过4，5，6 号阀门以及7 号压载舱隔离阀件，进入压载舱，压载工作完成。如遇紧急情况，或者阀门损坏，海水可不通过AZ，直接经由7 号阀门进入压载舱。其中2 号压载泵为备用，如遇紧急情况，1 号压载泵和2 号压载泵同时工作。

卸载即为系统排水，卸载流程为打开4 号压载隔离阀件，1 号压载泵开始工作，将水抽出，经7，8，1，2，3 号阀门进入AZ，水质达标后排除舷外。当压载水低于某一容量时，需扫舱系统将剩余压载水排除，即关闭1 号压载泵，通过扫舱泵将压载水排出。

通过对于压载水系统工作流程的介绍，可以得到压载水系统故障事件，如表1 所示。

表1 故障事件Tab. 1 Fault event

动态故障树为包含动态逻辑门的故障树。由于故障事件间具有关联关系，所以采用动态故障树来分析故障原因。以压载水系统为顶端事件来建立故障树。为了方便分析故障事件的关系，引入部分中间事件作为过渡。

由图2 可以看出，故障事件由逻辑门连接起来。以压载水系统失效Z为顶端事件，其中Y1和Y2分别为失效事件，只要吸水不成功或者排水不成功，压载水系统即失效。对于Y1来说，X1，Y3，Y4、X2只要有一个事件失效，Y1即失效，所以逻辑门关系为或门。同理其余类似事件的逻辑门关系也应为或门。但对于事件Y4压载泵失效来说，在特殊情况下2 号水泵与1 号水泵，均要工作，所以事件X4、X5的逻辑门应为热备门。事件Y11和X11同时失效，事件Y8才失效，应为与门。

图书馆流通部是联系图书馆与读者之间的桥梁和纽带，但是大多数高校都存在着领导对此不够重视，认为流通部工作简单，没有技术含量，对流通部员工管理及一些借阅制度都是延续多少年以来的老办法，没有新意，没有奖励激进措施，而流通部工作又单调乏味、繁重，这样就会使馆员工作懈怠，始终处于应付状态，对读者缺乏关心和耐心，势必会影响流通服务质量，破坏图书馆整体形象。

图2 压载水系统故障树Fig. 2 Ballast water system fault tree

2 压载水系统可靠性模型

连续贝叶斯网络能够表示系统在连续时间下的性能。由于船舶压载水系统组件众多，系统性能随时间变化较为明显，因此连续贝叶斯网络能够较好的刻画系统性能。船舶压载水系统故障树转化为贝叶斯网络的过程中，需要借助单位阶跃函数和冲激函数[9]实现转化。

单位阶跃函数为：

冲激函数为：

其中，变量t和η分别表示事件的失效时间。

图3 为逻辑与门的故障树结构和转化后的贝叶斯网络。当事件Y11和事件X11同时失效后，事件Y8才失效。根据逻辑或门的失效机理和贝叶斯网络的性质，可以得到事件Y8的失效条件概率为：

图3 与门转化为贝叶斯网络Fig. 3 AND gate is converted to Bayesian networks

其中，y11、x11、y8分别表示事件Y8、事件Y11、事件X11的发生失效的时间。v(x11-y11)ζ(y8-x11)表示事件Y11先失效时，事件Y8随着事件X11失效而失效；v(y11-x11)ζ(y8-y11)表示事件X11先失效时，事件Y8随着事件Y11失效而失效。

根据贝叶斯网络的性质可知，该逻辑与门的联合概率密度函数为：

将此联合概率密度函数对y11和x11积分，得到事件Y8的概率密度函数为以及概率分布函数为：

图4 或门转化为贝叶斯网络Fig. 4 Or gate is converted to Bayesian networks

其中，x6、x7、y6分别为事件X6、事件X7、事件Y6的发生失效的时间。v(x6-x7)ζy6(y7-x7)表示上级事件X6先失效时，下级事件Y6随着上级事件X6失效而失效；v(x7-x6)ζ(y6-x6)表示当上级事件X7先失效时，下级事件Y6随着上级事件X7失效而失效。

根据贝叶斯网络的性质可知，该逻辑或门的联合概率密度函数为：

将此联合概率密度函数对x6和x7积分，得到事件Y6的边缘概率密度函数为以及概率分布函数为：

因此，在(-∞,t)上对事件Y6失效的边缘概率密度函数积分，可得到下级事件Y6失效过程的概率分布函数为：

图5 为热备门的故障树结构和转化后的贝叶斯网络。压在水泵1 工作时，压载水泵2 也工作，当压载水泵1 和2 均失效时，事件Y4才失效。根据动态贝叶斯网络的性质，X4在X5失效的条件下，失效的概率为：

图5 热备门转化为贝叶斯网络Fig. 5 Hot spare gate is converted to bayesian network

又因为只有事件X4、事件X5均发生失效时，事件Y4才失效，因此，事件Y4失效的条件概率函数可由动态逻辑与门的条件概率得到，其条件概率可以表示为：

根据贝叶斯网络的性质可知，该热备门的联合概率密度函数为：

上述联合概率密度函数对变量x4和x5积分，可得下级事件Y4的边缘概率密度函数和概率分布函数为：

3 算例分析

船舶压载水系统结构复杂，故障形式多样，故障事件间具有错综复杂的关系。借用上述分析，将压载水系统动态故障树转化为连续贝叶斯网络模型，以便于分析压载水系统的可靠性和剩余寿命。基于图2 中的船舶压载水系统故障树，可以得到系统的连续贝叶斯网络模型，如图6 所示。

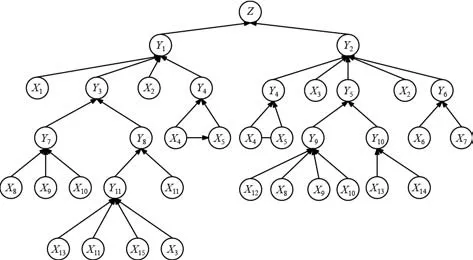
图6 连续贝叶斯网络模型Fig. 6 Continuous bayesian network model

通过转化后的贝叶斯网络，基于表1 中的数据，利用式（6）、式（10）、式（15），可以得到船舶压载水系统可靠度随时间的变化，如图7 所示。

图7 系统可靠性变化曲线Fig. 7 System reliability change curve

可以看出，船舶压载水系统随着时间的变化，可靠度逐渐降低，当t=153h，系统可靠度已经降低到0.495 5；当系统运行到t=348 h 时，系统的可靠度降低为0.207。系统可靠度下降的速度逐渐变缓。

利用船舶压载水系统的可靠度，通过对系统可靠度在（t,∞）的积分，可以得到t时刻系统的剩余寿命其中，u代表系统寿命。可以得到船舶压载水系统的剩余寿命随时间的变化，如图8所示。

图8 系统寿命变化曲线Fig. 8 System life curve

根据图8 以及仿真计算，船舶压载水系统，在0 时刻剩余寿命为219.76 h，随着时间的递增，剩余寿命逐渐变短；在t=348 h 剩余寿命为45.54 h。系统的剩余寿命随时间变化的速度逐渐递减。

4 结 语

针对船舶压载水系统结构复杂，可靠性难以分析的问题。本文基于船舶压载水系统的故障机理，建立了压载水系统的动态故障树模型。然后基于连续时间的贝叶斯网络，通过算例分析了船舶压载水系统的可靠性。