基于A2C算法的低轨星座动态波束资源调度研究
刘伟,郑润泽,张磊,高梓贺,陶滢,崔楷欣
1.国家航天局卫星通信系统创新中心,北京 100094 2.中国空间技术研究院 通信与导航卫星总体部,北京 100094 3.西北工业大学,西安 710072 4.北京理工大学,北京 100081
1 引言
随着未来天基信息网络的战略谋划、快速建设和创新应用,对海、陆、空、天不同类型用户的天基信息支持将在社会民生、市场经营、国家安全中发挥越来越重要的作用。当前,国外科技巨鳄已经开始如Oneweb、Starlink等低轨星座的建设和商业运行[1],并谋求为地面用户提供多样化的天基信息服务。低轨星座卫星的轨道高度远远低于地球同步轨道高度,位于500~2000km之间。在信号衰减、传播时延、灵活发射、弹性抗毁和研制成本方面具有显著优势[2],同时相对于地面信息网络在全球覆盖方面具有突出的优点。
当前低轨星座波束资源调度研究主要方向包括对地表用户的接入覆盖、波束功率频率资源的分配等,面向用户航天器如运载火箭、载人飞船、空间站、遥感卫星通信需求的研究成果还比较少。本文面向中国未来低轨星座的建设与应用,通过对低轨星座动态波束资源调度场景进行建模,开展预先研究。旨在多星、多波束、多用户场景下选择最合适的波束资源为用户航天器提供服务,以缓解日益凸显的数据回传与通信服务需求和有限的波束资源之间的矛盾。
使用低轨星座为用户航天器提供服务的主要约束来源于用户任务需求和波束资源状态两方面,涉及到任务数量、波束数量、任务持续时间、资源可用时间、通信建链时间等具体内容。因此,低轨星座动态波束资源分配是一类多约束的组合优化问题,对于卫星资源动态调度(DBRS,dynamic beam resource scheduling)领域的相关问题,A.Aroumont等人在文献[3]中提出了一种无线电资源管理算法,该算法通过衰减减缓技术提高了资源利用率。在文献[4]中,D.K.Petraki等人认为卫星资源分配问题可以用博弈的思想和算法来解决,如采用马尔可夫链模型形成议价模型。D.Shi等人提出了一种改进的布谷鸟算法来优化[5]中的卫星资源分配。在文献[6-9]中提到了基于多波束的DBRS建模。其他DBRS问题求解的相关研究均列于文献[10-13]。
然而这些资源分配成果主要面向传统高轨中继系统、低轨星座对地覆盖场景和涉及通信体制的功率带宽分配,在强动态、高切换的低轨卫星通信波束资源调度领域的有效性还未进行验证。
基于强化学习框架的资源分配算法被广泛关注并形成丰硕成果[14]。在文献[15-16]中,基于强化学习的算法分别成功地解决了低延迟无线接入网络和智能移动边缘计算系统下的动态资源分配问题。在文献[17-18]中,采用强化学习的算法,解决了与通信相关的动态资源分配问题。文献[19-23]中列出强化学习在资源分配领域的其他成果。鉴于强化学习框架在资源分配问题中的出色性能,本文采用将其作为低轨星座动态资源调度问题的基本框架。
其中基于值(value-based)和基于策略(policy-based)是强化学习领域的两类重要方法,基于值方法试图寻找最佳值函数,值越高意味着动作(action)评价越好,基于策略方法则尝试直接找到动作最佳策略。本文采用的A2C架构结合了两种方法的优点,其核心思想是将模型分为两部分,一部分用于根据状态(state)计算动作(基于策略),一部分用于评估动作的Q值(基于值)。本文将低轨星座波束资源的动态调度场景抽象为序列预测问题,以符合A2C算法的应用逻辑。在智能体(agent)执动作用过程中采用了基因遗传算法中个体(任务规划结果)和基因(用户任务)的概念,通过基因的操作实现智能体的动作。在动作评价方面采用了多参数多权重的评价函数,可根据动作状态自适应调整权重以优化评价方法。本方法与传统顺序更新法相比,能够在较短的时间内形成最优规划策略,且理论上可以在任何合适的应用环境(environment)下快速获得最优分配方案,这对低时延的用户服务体验是重要的。
由于本强化学习框架没有直接的引导信息,智能体需要不断与环境交互,通过多个回合试验获得最优策略。传统A2C算法的难点在于训练过程中每一回合每一次更新步骤之间强相关的环境特征会存在无法收敛的问题。本文提出了一种基于卷积网络的环境反馈提取设计使得算法在快速获得资源调度结果的同时还避免了无法收敛的问题。
2 动态波束资源调度问题数学模型
图1中给出了多用户动态、并发提出用户接入需求的场景,本文提出的动态波束资源调度算法就是要满足复杂约束下航天器用户的接入需求产生的波束资源分配问题。
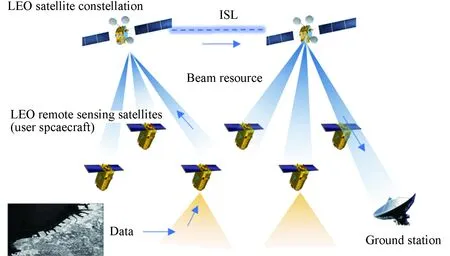
图1 低轨星座波束服务航天器用户场景
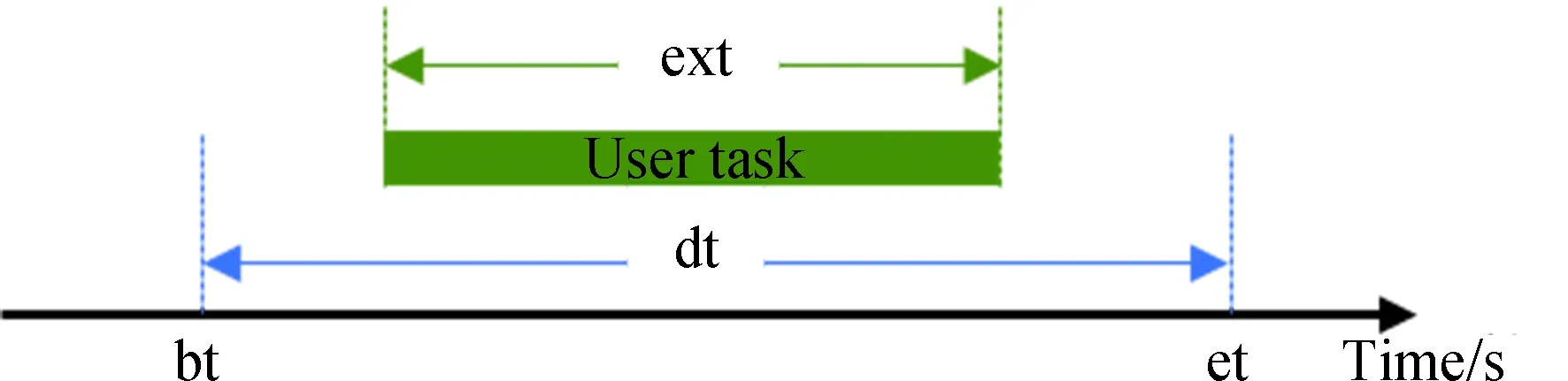
图2 用户任务模型示意图
场景中的主要要素包括低轨星座卫星、用户航天器、用户任务、波束资源等部分。每一个低轨星座卫星会有若干波束资源,每一个用户航天器会产生若干用户任务。
2.1 动态资源调度场景数学模型
低轨星座波束资源调度优化旨在解决多个用户需求和多个波束资源之间的匹配问题,其数学模型中主要包括波束资源分配时间窗口、用户航天器、用户任务、低轨星座卫星、及波束资源、可见时间窗口以及通信链路建立的数学模型。本模型中,设置波束资源分配时间窗口为T=[Ts,Te],其中Ts为窗口起始时间(默认取值为0),Te为结束时间。将根据此时间窗口内的所有用户需求和波束资源进行分配优化。按照时间切片长度t进行划分,波束资源分配时间窗口内则会包含tot=(Te-Ts)/t个连续的时间切片,尽量选取(Te-Ts)为t的整倍数以保证时间切片数量为整数。
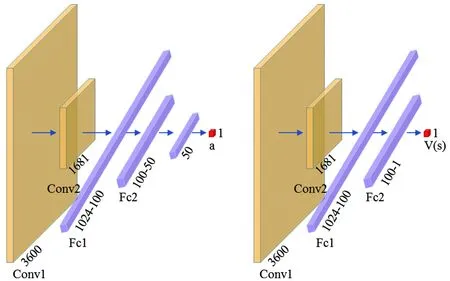
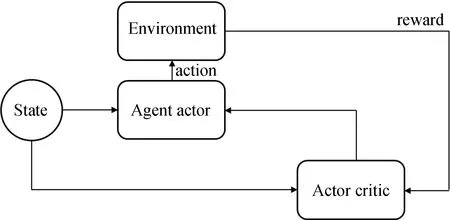
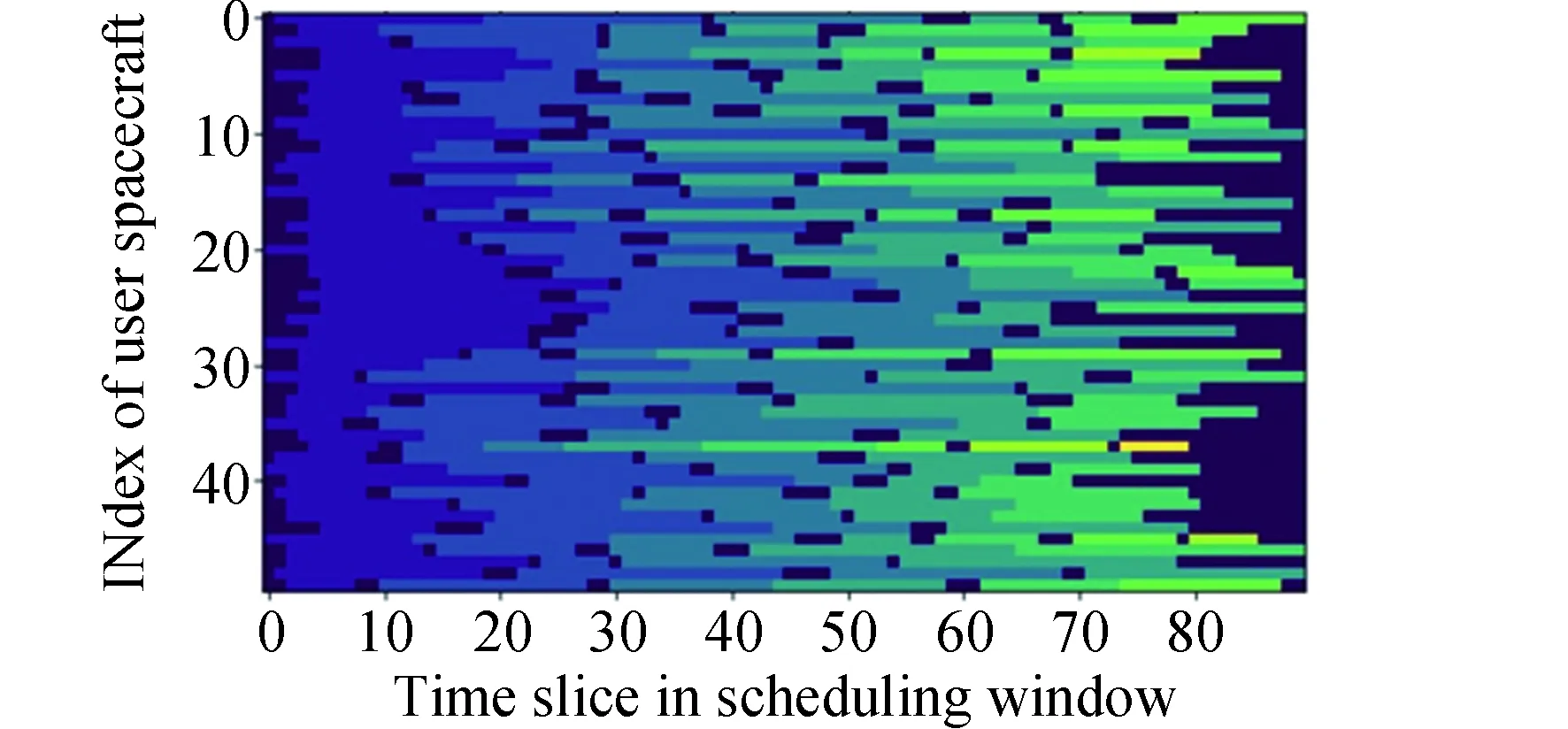
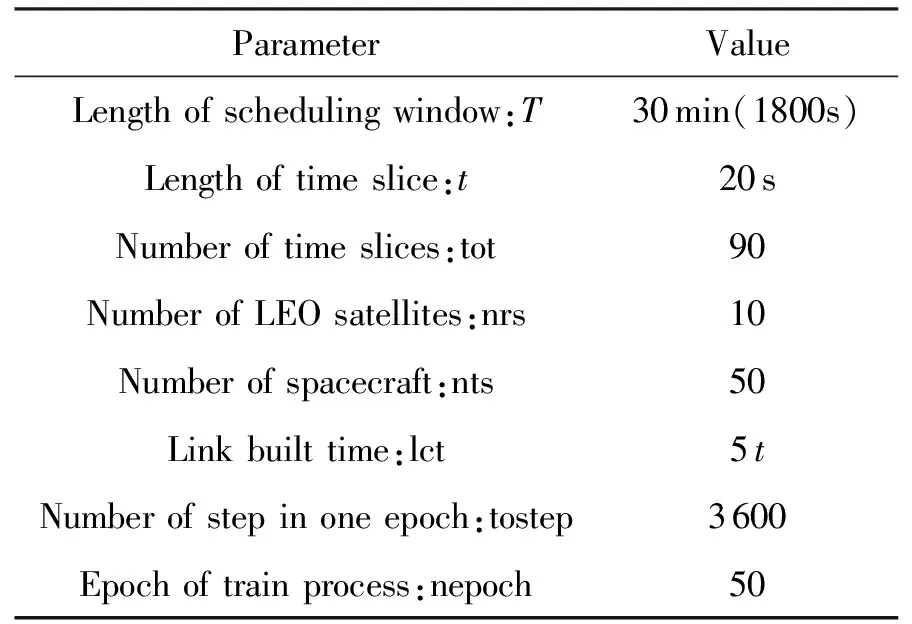
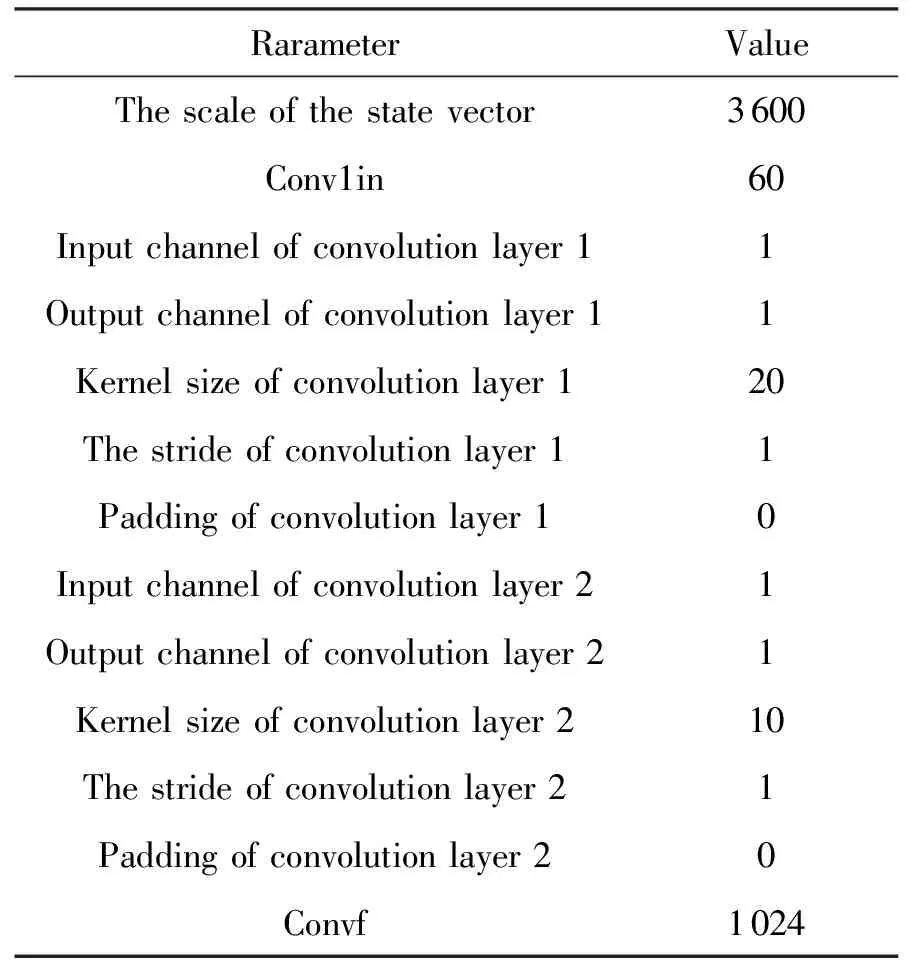
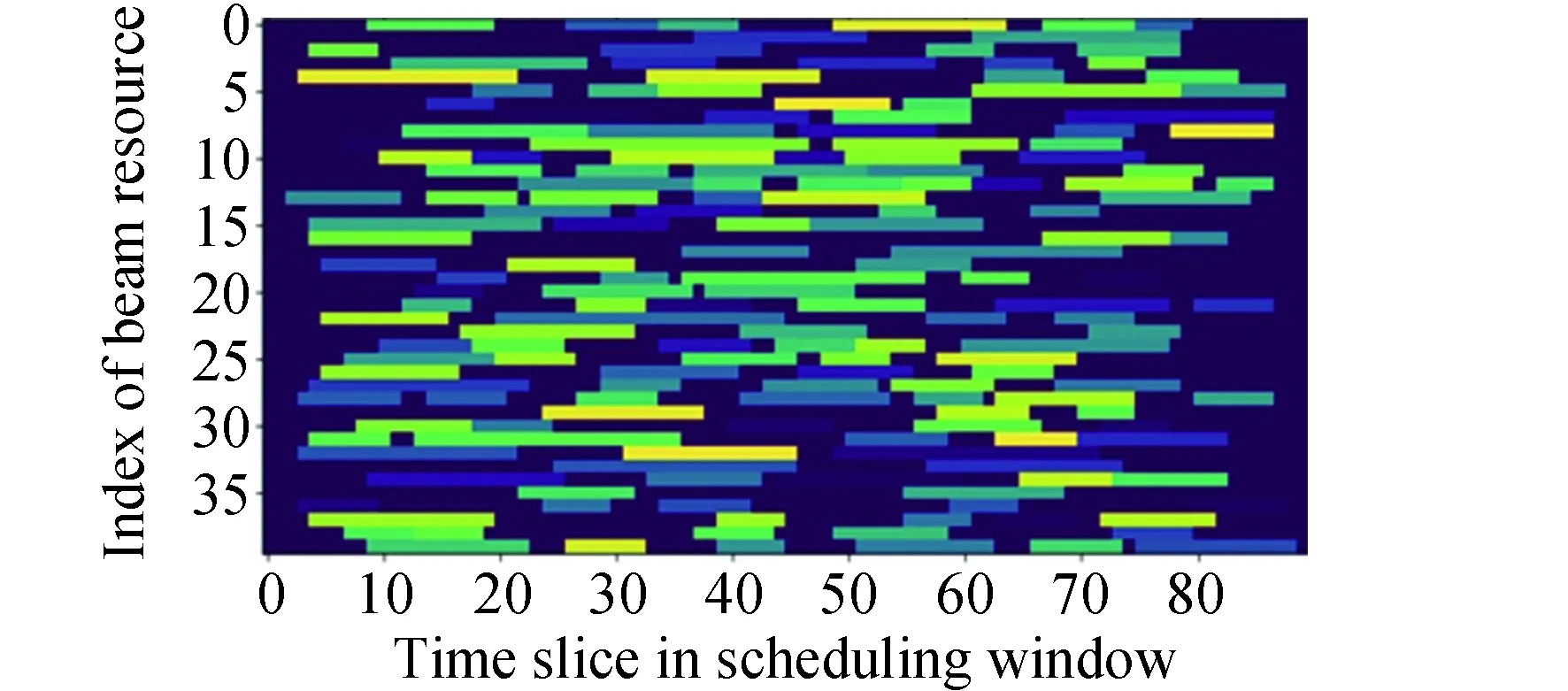
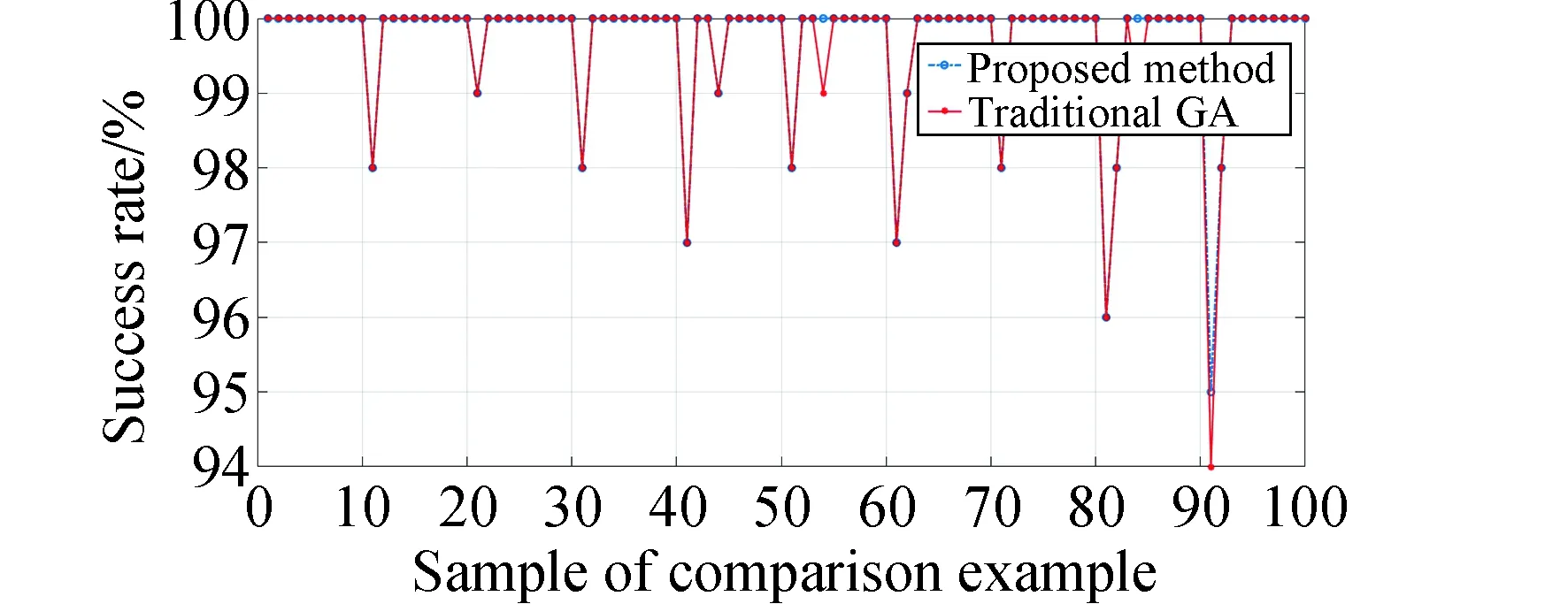
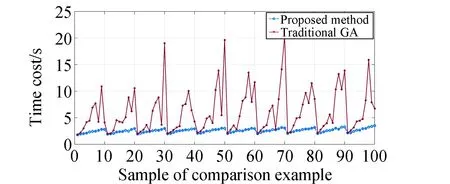
本模型中,设置用户航天器数量为nts,每一个用户航天器编号分别为tsj,用户航天器最多可以生成tmax个用户任务,用户任务编号分别为tsjm,每个任务的可用的起始时间和终止时间分别为btjm和etjm,每个任务可用时间dtjm为两个时间的差值,每个任务实际持续时间长度为extjm,其中下标j为用户航天器的索引,j∈{1,2,…,nts}。下表m为用户任务索引,m∈{1,2,…,tmax}。不同用户任务起止时间需满足btjm 本模型中,设置低轨星座卫星数量为nrs,每一个低轨星座卫星的编号分别为rsi,且每个卫星拥有nbc=4个可用波束资源,每个波束资源编号为rsik,下标i为低轨星座卫星的索引,i∈{1,2,…,nrs}。下标k为波束资源的索引,k∈{1,2,3,4}。 本模型中,用户航天器和低轨星座卫星只有满足可见时间窗口的约束时波束资源才可被分配给用户以执行数据传输业务。可见时间窗口用矩阵KJ=[visij,vieij]表示,visij表示第i个低轨星座卫星和第j个用户航天器之间可见时间窗口的起始时间,vieij表示对应的结束时间。 用户航天器和低轨星座卫星在开始业务传输之前需要进行波束指向对准,需要占用的时间长度为lct。因此每个任务需要占用波束资源时间长度attjm为任务实际执行时间长度extjm和建链时间lct之和。除此之外,低轨星座卫星每一个波束资源每一时刻只能为一个用户航天器的一个任务进行服务。 为了表述方便,设置三维矩阵ES来存放用户任务的相关重要参数。ES有j行、m列、7层,对应用户航天器用户任务的7个关键参数[j,m,p,bt,et,dt,att],不同参数需满足以下约束关系。 btjm pjm∈{1,2,3,4} dtjm=etjm-btjm attjm=extjm+lct lct 式中:用户任务的可用的结束时间et必须大于开始时间bt,任务优先级取值范围为{1,2,3,4};用户任务可用时间长度dt为结束时间et和起始时间bt的差值,实际占用波束资源的时间att为任务实际时间ext和建链时间lct之和,且小于用户任务可用时间dt。 设置VIS和VIE矩阵用于存储nrs个低轨星座卫星和nts个用户航天器之间可见时间窗口的起止时间。每个矩阵包含nrs行和nts列,VIS矩阵中的visij元素表示第i个低轨星座卫星和第j个用户航天器之间可见时间窗口的起始时间,VIE矩阵中的vieij元素表示第i个低轨星座卫星和第j个用户航天器之间可见时间窗口的终止时间。 用户任务和波束资源之间匹配过程是选择能够满足用户任务tsjm需求和约束的波束资源rsik并占用该资源。一旦波束资源被某一任务占用,则被占用的部分不能再用于服务其他用户任务。假如att对应的起止时间为[pts,pte],则需满足下述要求: visij≤pts 即最终用户任务执行时间(包括任务自身时间和建链时间)必须为可见时间的子集。 由此可见,在波束资源分配时间窗口内的资源是确定的,用户任务也是确定的。如何在满足约束的条件下,利用有限的资源满足尽可能多的用户需求与任务优先级高的任务,是本文研究内容的主要目的。 根据上述场景的数学模型设置三个二维矩阵TSM、DUR和REW用于记录任务规划算法求解过程中的输入和中间输出信息。其中,用户任务信息矩阵TSM中包含nts行和tot列。每一行代表一个用户航天器,每一列代表波束资源分配时间窗口内的一个时间切片。矩阵中元素的值为用户任务的编号tsjm,以反映用户任务的具体顺序和时间信息。资源分配结果矩阵DUR中包含nts行和tot列,矩阵中的元素值为任务对应波束编号的rsik,反映的是用户实际占用波束资源的时间长度att(包含lct和ext两部分),以及具体的起止时间信息。任务奖励矩阵REW中包含nts行和tot列,矩阵中元素值为与DUR矩阵中的对应位置上对应用户任务的即时任务奖励。每个用户任务的奖励rjm定义为: irjm=pjm rjm=irjm*attjm 式中:pjm为第j个用户航天器第m个任务的优先级。 当某一个波束资源与一个用户任务匹配时,将从TSM、DUR和REW中收集该用户任务的相关信息,并使用xjm作为任务是否选择的标识。 式中:0表示未选中任务航天器j的第m个用户任务,1表示选中。因此,所选择的每个任务对应获得的任务奖励可以描述为: obirjm=xjm*irjm obrjm=xjm*rjm 将nrs个低轨星座卫星的所有波束资源定义为模型的单一智能体(agent)。创建一个4*nrs行和tot列的矩阵SR,其中行表示4*nrs个波束资源,列表示tot个时间切片。SR中的元素记录的是动态波束资源调度窗口内的动作(action)信息。在每个资源调度回合中需记录的总步数为: tostep = 4×nrs×tot 此外,SR与状态矢量同步,并具有轨迹记录的功能。 为了避免不同参数对应问题模型性能无法直接比较算法效能的问题,设计归一化u来衡量波束资源分配优化算法生成的调度方案的性能。其定义为成功获得波束资源的任务获取的奖励回报Ro和环境总任务的奖励回报Rt的比值。换句话说u值越大,动态资源分配优化算法的效果就越好。 u=Ro/Rt 传统强化学习模型与算法中往往仅有一个输出量,策略或值[18]。AC(actor-critic)算法兼具两种变量输出的能力,其中通过演员(actor)网络来学习动作(action)的策略,输出动作策略。通过评价(critic)网络来学习对动作的评价,输出评价值。本文算法中动作采用了基因遗传算法中基因突变的类似的概念以提升算法效率。通过多要素的线性优势函数替代AC算法中评价网络的原始回报,通过设计自适应评价参数更新机制可以衡量智能体的动作与平均动作的差异并采取优势动作。意味着本文算法对动作的评价不仅取决于动作的良好程度还取决于动作可以改善的程度。 传统A2C算法指导智能体的动作决策由演员网络AN和评论网络CN完成,θ和w为两个网络的重要参数,这且两个神经网络的参数都是基于单步更新的。由于单步更新策略下的环境反馈存在强相关性,导致了该算法在优化求解时可能会因为不收敛而无法进行有效学习。为了解决此问题,本文通过引入中间卷积层来消除强相关性。卷积层的输入形式为从大小为tostep的一维向量变形得到的conv1in*conv1in的二维矩阵,其中 tostep=conv1in×conv1in 将该二维矩阵作为卷积层的输入,通过两层卷积过程获得卷积特征向量convf,并为AN和CN的输入。卷积过程如图3所示,其中图左为AN,右侧为CN。其输出结果分别为对应单步的智能体动作以及状态值函数。算法具体过程如表1所示,这种方法在解决强相关环境反馈引起的算法不收敛是有效的,通过改变卷积层参数,可以解决不同规模的各种环境反馈的强相关性问题。 表1 卷积特征提取 图3 神经网络输入卷积处理过程示意 在强化学习算法中,智能体感知环境状态,并根据之前从环境反馈得到的奖励(reward)选择动作。在波束资源动态分配场景中,智能体为一个可用的任务规划结果,动作是用户任务和波束资源对应关系的调整。对于每一个波束资源调度回合中离散的步骤,智能体可以选择若干用户任务并改变当前的资源分配结果作为其在此步骤的动作,在经判定有效后得到对应任务奖励。 状态、动作、奖励(reward)的具体定义如下: (1)状态 状态向量State是一个包含tostep个元素的一维向量表示,每个资源调度回合中的状态向量元素值的初始化默认为0。状态向量中的0表示当前每个低轨星座卫星上波束资源为空闲状态。在每一个时间步,智能体的行为可以为选择一个任务卫星索引j,环境根据智能体做出的动作返回相应的下一个状态向量以及对应的即时任务奖励;智能体也可以选择不选择任务卫星在此时间步保持对应波束资源的空闲状态。 如果状态矩阵中对应的元素在一个时间步内不为0,则当前操作决策将不会被定义为有效。一旦确定动作是有效的,这意味着低轨星座卫星和用户航天器匹配时间在可见时间窗口内,用户任务也可以在可见时间窗口内完成。然后将所选任务卫星编号写入当前状态向量,使该波束资源在后续的时间步中无法选择其他任务,直到当前任务完成。所选择的任务卫星的信息将从TSM矩阵中删除,使该任务无法被资源卫星上其他未占用的波束信道选择。 State=(sstep=1,sstep=2,…,sstep=tostep) 其中状态向量中的每个元素对应回合内智能体所选择的相应动作,回合结束所得状态向量即为回合智能体动作序列。为了节省算法对计算和存储资源的占耗,算法中将每个回合内的状态通过评价函数转换为收益值,以节约存储资源。 (2)动作 动作的定义是将不同的用户任务随机的分配至可用的波束资源上,每一次动作都会形成新的具有不同收益的智能体。考虑到每个用户航天器只有一个通信波束的约束,同一个低轨卫星波束资源在某个时间切片上,只允许对应一个用户任务。所选择的动作将记录在状态向量及其记录矩阵SR中,每一步的动作定义为: 式中:astep=0表示在该步骤没有选择任务卫星;astep=j表示在该步骤选择任务卫星索引为j。 (3)奖励 奖励的定义是成功规划任务数量与任务优先级的线性组合。每个任务的即时任务奖励可以从矩阵REW中获得。使用向量R去记录每个回合中的单步即时奖励。向量R中元素值的最后一个值为每个回合获得的最终任务奖励。为了节约对存储资源的占耗,REW中在每次回合结束后将最后一个奖励值输出后进行清空,以重复使用该变量并节约存储空间。 为了让智能体能够学习到最优的资源分配策略(π),波束调度算法具体实现有两种方式,其一基于贪心算法的资源调度回合中每一步更新过程具体如下:①基于当前状态向量,AN网络根据ε-贪心算法选择一个输出动作或者在动作空间中随机选择一个动作。一旦所选择的动作步骤被评估为有效的,环境将返回相应的即时奖励和下一个状态向量。②然后CN将动作、即时奖励、当前状态和下一状态作为输入产生TD误差δπθ,其中TD误差是对优势函数Aπθ(s,a)的无偏估计,本文A2C算法采用的优势函数的定义如(1)所示。无偏估计和TD误差的计算公式如(2)和(3)所示。 Aπθ(s,a)=Qπθ(s,a)-Vπθ(s) (1) Aπθ(s,a)=Eπθ[δπθ|s,a] (2) δπθ=r+γπθ(s′)-Vπθ(s) (3) 在公式1的优势函数中,s为智能体当前状态,a为智能体当前动作,πθ为当前执行的策略。Qπθ(s,a)为动作价值函数,表示智能体处于状态,πθ在采用动作a后的预期回报。Vπθ(s)为状态价值函数,表示当智能体处于状态S时基于策略πθ的预期回报。公式2中的Eπθ[δπθ|s,a]即为基于当前状态和动作求TD误差并取期望。公式3中的r为奖励回报,γ为奖励衰减率,Vπθ(s′)代表基于下一个状态,s′的价值函数值,γπθ(s)代表基于当前状态s得到的价值函数值。 CN使用均方误差(MSE)方法基于TD误差更新其参数w,然后将计算出的w传递给AN,AN使用策略梯度方程更新其参数θ。这一过程将持续进行,直到一个资源调度回合结束,具体过程如图4所示。具体算法过程如表2所示。 表2 动态资源分配 图4 A2C算法流程示意 图5 原始任务甘特图 θJ(θ)=Eπθ[θlogπθ(a|s)δπθ] 第二种方式是通过线性评价函数对智能体的动作进行实时评价,该评价函数包括用户任务规划状态、该任务的优先级绝对值和波束的切换次数。该函数可同时评价对用户任务需求的响应和对系统资源的占耗。 式中,x为当前智能体中成功规划任务对应的标志,取值为1;P为所有成功任务对应的优先级绝对值,SW为当前智能体对应波束切换次数(越小越好)。权重α,β,λ影响每一个量对评价函数的贡献。CF的值越高,说明智能体采取该动作获得的奖励越高。 这两种方式均可以使得智能体学习动作选择的策略,方式一中可以在较短回合数内完成策略的选择,由于每一回合中计算较为复杂占用时间反而较长。第二种方式需要在全部求解空间内进行搜索,需要较多的回合数能够发现动作偏好,由于每个回合中计算过程较为简单,用时反而较少。 本部分从三个方面(有效性、适用性和不同算法对比)对提出的算法进行了仿真分析。根据仿真环境性能的差异,相同的场景配置参数产生的时间消耗、计算资源占用数值可能不同。 建立一个典型场景用于验证低轨星座波束资源算法的有效性,其中设置50个用户航天器在波束资源分配时间窗口长度为30min的时间内随机生成若干不同优先级的用户任务。每一个用户任务所需时间为时间切片(t=20s)的整倍数,取值范围为1t至20t,即每个用户任务可能的持续时间为20s到400s不等。用户任务得到执行需要的时间包括任务本身的时间和建立链路所需的时间之和,其中lct取值为100s。仿真采用的是Python语言、Matlab和Torch深度学习框架。仿真环境为主频为2.6GHz内存为16GB的通用计算机。用户任务甘特图如5所示,仿真具体参数配置如表3所示。 表3 仿真配置参数 图中横轴代表时间,共包含90个时间切片。纵轴为用户编号,对应50个用户航天器。其中每一个有色条块代表该用户航天器在不同时间产生的用户任务,共计207个任务。该图同时能够反映每一个任务的可用的起止时间信息。 算法在进行资源分配时需要考虑每一个用户航天器和低轨星座卫星的可见时间是否能够满足任务本身和建链时间的约束。其中可见时间的visij从[0,45]中随机得到,vieij从[45,90]中得到,意味着可见时间长度取值范围为[0,90]。 基于3.2中方式一,提出的算法在应用卷积层从环境反馈中提取特征时,经对不同范围参数的测试,最终得到了收敛速度最快、实验效果最好的参数配置结果,卷积层参数如表4所示,两组网络配置参数如表5所示。 表4 网络配置参数 表5 AN/CN网络配置参数 在上述仿真模型中对提出的算法进行仿真,波束资源分配结果如图6所示。 图6 任务规划结果 图中横轴代表时间,对应30min内的90个时间切片。纵轴对应40个波束资源编号,其中的有色条块代表不同的用户任务被分配在对应波束资源上占用的时间。每一个有色条块的长度包含建链时间和任务本身持续时间两部分。成功调度任务数为169个,成功率不低于80%,其中任务失败原因主要是由于没有足够的波束资源。使用40个波束资源服务50个用户存在较多的资源冲突。该仿真结果可验证提出算法在任务规划中的有效性。 为了进一步验证动态波束资源调度算法的灵活性和适用性,设计了不同场景并进行针对多种结果进行了仿真分析。对比实验共分为三组,其中场景参数主要包括用户航天器数量nts、资源卫星数量nrs、每颗资源卫星波束数量nbc等。场景1为典型高轨场景、场景2为典型中轨场景、场景3为典型低轨场景,具体参数设置如表6所示。 表6 对比实验场景参数 仿真结果主要包括不同场景下用户任务的数量TN、被成功调度的任务数量STN、任务规划成功率SR、仿真时间消耗TC等信息。仿真对比结果如表7所示。 表7 对比实验仿真结果 由于可用波束资源数量少于用户航天器数量故而存在部分由于资源短缺导致的任务规划失败。上述仿真场景中,任务规划成功率不低于91%,该算法在不同场景配置下能够有效的进行任务规划,具有多种场景的应用灵活性。 同时仿真结果表明,随着用户任务数量的增加,算法仿真产生的时间消耗也明显增多。面对用户航天器快速请求响应的需求,任务规划算法时间消耗不应大于18s(一个时间切片内可用于计算的时间),当航天器最大任务数超过2600时,算法响应时间为18.4s,因此算法在面对大量用户任务场景下存在使用局限,需要针对天基算力受限的场景提出如任务分割和分布式计算等方法进行解决。 由于该算法的应用对象是资源受限型的低轨卫星,算法的复杂度直接影响了工程应用的实现难易程度。本算法的计算复杂度由定义的状态空间、动作空间以及应用的网络的大小规模所共同决定。面向星载算力受限的场景最直观的体现在算法对CPU处理器、RAM内存的占用上。在算法设计过程中重点优化了对CPU和内存资源的消耗,如减少非必要的循环语句和非必要变量,通过降低算法复杂度以实现对系统要求的降低。将该算法使用Golang语言进行编译,并在上述仿真环境中进行仿真,对CPU和RAM的占用随时间波动,结果取平均值,三种对比场景下的资源占耗如表8所示。 表8 计算占用仿真结果 结果表明,相同的仿真环境下,不同场景中产生的资源占耗较低,CPU占用不大于5%,RAM占用不大于20%。 为了验证本算法在响应速度和任务规划成功率方面的优势,分别与传统全连接的A2C算法、DQN算法和传统双链基因遗传算法进行了对比仿真分析。 仿真对比一:由于3.2中方式一和全连接A2C算法和DQN算法架构较为类似,进行仿真对比,其中仿真场景参数包括nts=70,nrs=20,nbc=4;三种算法奖励值结果u如图7所示。 图7 不同方法50回合学习结果u 图中横坐标代表回合数(无单位),纵坐标代表的每回合生成的调度方案的奖励值u(归一化值,无单位)。其中u值越高,意味着资源和任务的匹配程度越高,相应的调度方案性能越好。 本算法相对传统全连接A2C算法解决了无法收敛的问题,相对于DQN算法可以达到相似的奖励值,但是达到收敛的所需回合数更少,其中本算法在第8代达到收敛,DQN算法在第13代达到收敛,本文算法收敛速度提升38%以上。 仿真对比二:采用3.2中方式二与传统基因遗传算法进行对比。设计100个样本,其中nts取值范围为[45:54],nrs取值范围为[10:19],nbc=4;其中,当nts取值为45时,nrs分别从10取值到19,以此类推,共计100个仿真样本。如图8和图9所示,仿真结果包括两种任务规划方法的成功率和任务规划时间消耗。 图8 任务规划结果成功率 图9 任务规划时间消耗 结果中横轴为100个对比样本(无单位),纵轴为任务规划成功率(成功任务规划数/总有效任务数×100)。本方法与传统基因遗传方法成功率基本相同,略优于传统基因遗传方法。其中部分样本的任务成功率较低是由于资源不足导致的。如当nts为54时,而nrs为10时,可用波束仅有40个,无法同时满足54个用户航天器的接入请求,进而导致任务规划成功率会降低。 结果中横轴为100个对比样本(无单位),纵轴为每次任务规划产生的时间消耗。由仿真结果可知,随着nts和nrs的增加本方法时间消耗几乎不变,而传统基因遗传算法随着计算任务规模的增加时间明显增加,这是由于传统算法需要在每一回合中对任务规划结果进行编码(将用户任务和卫星编码为两条染色体)和解码(将染色体解码为任务规划结果)导致的效率降低。结合任务规划成功率对比结果可知,虽然两种方法在任务规划成功率方面几乎相同,但是在时间代价上本算法更具有优势,平均可节约时间达45%以上。 本文研究了低轨星座波束资源动态分配优化的问题,形成了基于A2C框架下的动态波束资源调度算法。经对比分析,形成以下结论: 1)本文提出的算法在进行波束资源分配优化问题求解中是有效的,当资源充足时任务规划成功率较高,当资源不足时任务规划成功率较低。 2)算法在多种场景下仍然具有适用性,通过场景参数配置可用于求解各种星座构型下的用户航天器接入问题。 3)算法在响应速度上具有优势,虽然与其他算法达到的任务规划成功率或总体奖励值相近,但时间开销相对较小,适用于时敏任务场景。 在后续的研究中,可面向算法复杂度降低开展研究,突破在星上算力受限的场景下工程应用。同时文中所使用参数和取值均面向验证本文方法和算法的有效性,与工程实际参数物理含义一致,但取值或许存在差异。2.2 优化求解数学模型
3 基于A2C的波束调度算法
3.1 回合单步环境特征提取

3.2 基于A2C框架的调度算法架构

4 算法效能评估
4.1 算法可用性评估

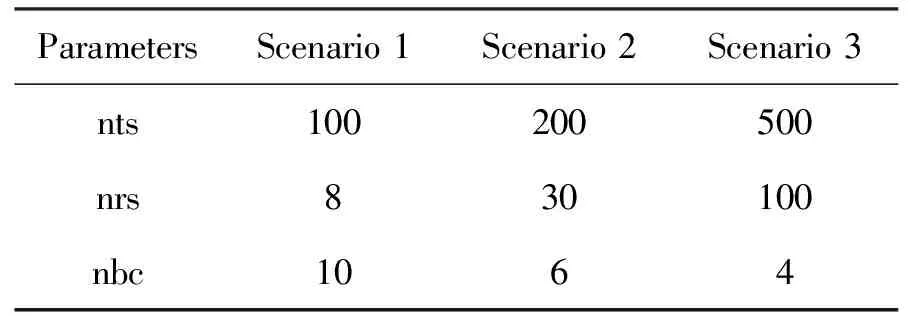
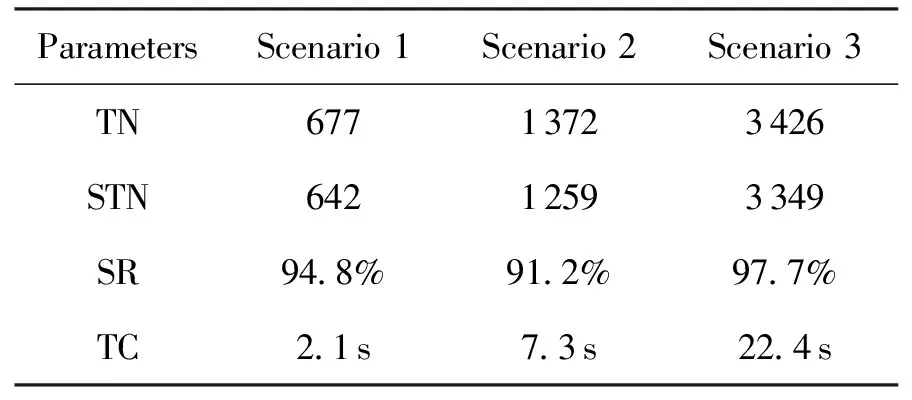
4.2 算法适用性评估

4.3 不同算法对比分析

5 结论

