基于FPGA的多方向阈值自适应Sobel算法实现

程伟涛 郭来功 汪强

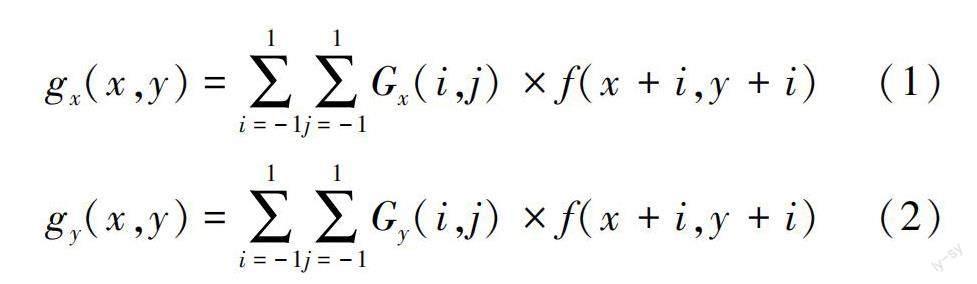
摘要： Sobel边缘检测技术是图像处理中最基本的技术之一。传统算法速度较慢且只有垂直和水平两个方向的梯度，对于一些其他方向的边缘检测效果不明显。文章设计了一种四方向（0°，45°，90°，135°）的Sobel算法来提高边缘检测的准确性，针对传统Sobel边缘检测算法阈值设置会出现偏差的缺点，基于中值滤波，采用自适应算法提高阈值准确性。本设计采用Verilog语言編程。仿真结果表明：多方向阈值自适应Sobel处理速度快，自适应阈值合理，边缘的完整性比传统方法有显著提高。

关键词：Sobel；自适应阈值；FPGA；MATLAB

中图分类号： TP391

文献标志码：A

0 引言

传统Sobel算子只有水平和垂直两个方向^［1］。传统Sobel算法具有阈值无法自适应的缺点。本实验采用多方向的自适应阈值Sobel算法^［2］，利用中值滤波的思想来实现自适应阈值。边缘检测在速度和准确性上，已经有多种提高方式^［3］。应用单片机、数字信号处理芯片来进行图像处理，采用串行方式，实时性和系统性能并不理想^［4］。因此，实验采用FPGA的瞬时并行处理数据的特点，可以满足实时性要求^［5］。FPGA这一特性的处理速度远远快于软件处理平台^［6］。

1 传统Sobel边缘检测

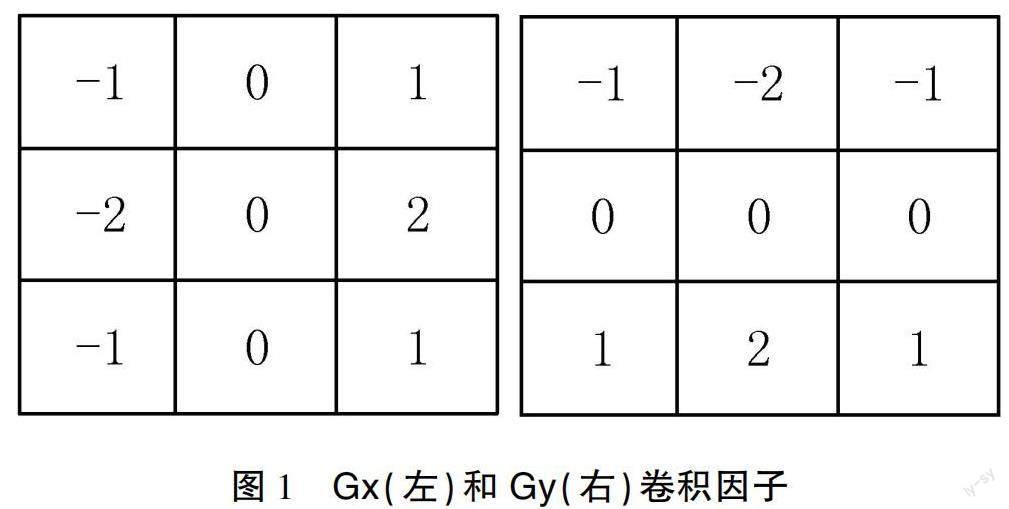
传统Sobel算子是一阶的边缘检测算子，采用的是x和y方向的两个3×3的卷积因子，记为Gx 和Gy，卷积因子由图1所示。

Gx为垂直梯度方向，用于检测水平边缘;Gy为水平梯度方向，用于检测垂直边缘^［7］，如图1所示。将x和y两个方向的卷积因子和原灰度图像对应位置的灰度值进行卷积，f（x，y）为图像的矩形窗口，见公式（1）和（2）。

选取一个3×3窗口的灰度值，记为：a₁、a₂、a₃、b₁、b₂、b₃、c₁、c₂和c₃。将它们和x、y方向的卷积因子分别进行卷积，得出结果就是x和y方向的灰度值，为g₁和g₂，根据公式（1）和（2）可得g₁和g₂的结果。根据公式（3）计算出这个3×3的窗口的梯度值大小，记为G_xy。但是考虑到FPGA的资源占用问题，本实验采用简单的绝对值求和的方式来计算最终的梯度值。如公式（4）：

G_xy=g₁+|g₂|（4）

实验计算出窗口的梯度值，然后进行图像分割。将公式（4）的结果和给出的阈值做比较，设阈值大小为T，大于阈值的赋值为1，小于阈值的赋值为0。

2 改进的Sobel算子

2.1 四方向Sobel算子

传统Sobel算子的检测方向只有x和y两个方向，当像素点其他方向的幅值较高，而x和y方向的幅值较低，传统算法无法检测到边缘点。本文在水平和竖直两个方向的基础上，增加了45°和135°两个方向，同样采用3×3大小的窗口，全部4个卷积因子如图2所示，从左到右分别是0°、45°、90°和135°，分别记为G₁、G₂、G₃和G₄。

将0°、45°、90°和135°方向的算子与目标窗口进行卷积，得到改进的梯度计算结果为记为g₁，g₂，g₃，g₄，见公式（8）：

将所求的4个方向的差分的绝对值相加，即为最终的梯度值，如公式（9）所示。

G_xy=|g₁|+|g₂|+|g₃|+|g₄|（9）

2.2 自适应阈值

计算自适应阈值通常采用大津法或基于直方图的方法等，这一类的算法较为复杂，一般应用于软件实现，而在硬件上这一类方法不太容易实现。本文参考的是中值滤波的思想，考虑到图像灰度值都是非负数，所以比较大小对的方式可以直接使用有符号数减法来表示。同时，本研究对张琪等^［5］的方法做出改进：第一步，在3×3的窗口中，先将每一行按照从大到小的顺序排列，得到一个新矩阵。第二步，找出这个新矩阵第一列的最大值（MAX_MAX）和最小值（MAX_MIN），第二列的中间值（MID_MID）以及第三列的最大值（MIN_MAX）和最小值（MIN_MIN）。第三步，找出第二步5个数值的中值，即为阈值T。这种方法所需要比较的数值较多，步骤较为烦琐，因此对第二步做出改进。第二步中第一列的最大值就已经确定为第三步的最大值，同理第三列的最小值也是第三步的最小值，因此可以直接将这两个数值去掉，在MAX_MIN，MID_MID，MIN_MAX中比较出中值。

3 系统框架

3.1 FIFO数据处理

Sobel数据处理采用的FIFO求和的思想。本实验选取一个3×3的窗口数据，因此采用FIFO来处理数据^［8］。两个FIFO的作用是缓存两行，可以得到三行数据。这里用到了FPGA的流水线特性，其优点可以实现数据的无缝缓存和处理，不仅节约了缓存区空间，而且提高了数据流的处理速度^［9］。

将数据写入寄存器之后，需要将寄存器里的数据进行Sobel处理，因此，再次定义一个读出标志信号，当行计数器计数到第三行的时候，将缓存的数据往外读出。对数据进行Sobel运算和阈值计算。

3.2 Sobel模块

数据由FIFO进入Sobel模块之后，由于时序信号需要延迟一个周期，因此，每一列的数据都会比前一列慢一个时钟周期，当FPGA标志信号有效时，可以得出Sobel计算所需要的9个数据。根据公式（8）和公式（9），计算出灰度值。模块由一个最高位判断框和一个数据选择器组成，当最高位是0时，表示正数，此时输出的绝对值就是本身，当最高位是1的时候，表示为负数，就需要对负数进行取反码再加一位。利用加法器和减法器计算出g₁，g₂，g₃，g₄，然后对这4个梯度值进行绝对值求和，所得结果为梯度值g_xy。

3.3 阈值自适应模块

4个方向的Sobel算法抗噪能力并没有多高，因此使用自适应阈值尽可能地避免噪声的干扰。本实验根据中值滤波的原理，找出窗口的中值作为图像的阈值，这种方法相对简单，易于实现。实验利用FPGA的并行特性，信号进入Sobel模块之后，分成两个方向，一个方向是进入Sobel灰度值计算模块，另一部分是进行阈值自适应。

3.4 边缘判定模块

边缘判定条件是阈值比较。计算所得的灰度值和自适应阈值模块给出的常数做出对比，大于这个常数，则判断为边缘，高电平为FF，显示为白色；小于或者等于给定的阈值，则判断不是边缘，为低电平00，显示为黑色。

4 实验结果与分析

本过FPGA对图像进行边缘检测。首先使用

MATLAB2018a版本对图像进行预处理。所处操作环境是Windows10系统，CPU为i5-7300，GPU为1050Ti。采用的数据是一个大小为541×541的Lena灰度图。经过QuartusⅡ13.1软件编写Verilog HDL语言来实现数据的传递、处理，通过Modelsim10.4和MATLAB双重验证算法的可行性。在Verilog的测试文件中，新建一个txt文件，将最终仿真的数据存入这个txt文件，然后在MATLAB中打开这个txt文件，得到最终的边缘检测图。图片选用的是一张541×541的Lena图。实验结果如图3所示。从a，b，c，d依次是原灰度图、人为设置阈值为116的传统Sobel检测图、认为设置阈值为70的传统Sobel检测图以及改进之后的自适应阈值的Sobel检测图。结合原图发现，图3（a）对比图3（d），两者使用同样的阈值，有4处比较明显的边缘没有检测到，由图中红色圈标记可以看出。图3（c）和图3（d）也有3处比较明显的差距。总体来说都是在45°和135°方向上差距明显，边缘的完整性比两方向的Sobel检测算法好。在运算速度上，FPGA的所用时间约为0.05 s，而传统Sobel时间约为2.63 s，速度提升了50倍。

5 结语

本文分析了边缘检测的作用以及传统Sobel边缘检测算子的优缺点，并针对缺点做出两处改进。第一个改进就是将边缘检测的方向由x和y两个方向增加到0°、45°、90°和135°4个方向。第二个是对阈值设定做出改进，将原先的人为设置改成自适应阈值。在速度方面，结合FPGA并行特性和流水性，运行速度高于软件的运行速度，处理一张大小为541×541的图片所用时间仅为0.05 s，而软件平台的处理时间为2.6 s，速度提升了50倍。对比传统Sobel算子，改进之后检测的边缘效果明显优于传统算法。

参考文献

［1］刘逢丁，曹杰，王营博，等.激光雷达距离像的实时边缘检测［J］.光学技术，2021（4）：404-409.

［2］陳磊，叶焱.多方向自适应阈值边缘检测算法及FPGA并行实现［J］.无线通信技术，2019（4）：21-26.

［3］ALMOMANY A，ALOMARI A M，JARRAH A，et al.An OpenCL-based parallel acceleration of a Sobel edge detection algorithm Using Intel FPGA technology［J］.South African Computer Journal，2020（1）：3-26.

［4］祁欣，陈剑锋，罗伟林.图像预处理算法的FPGA实现［J］.国外电子测量技术，2021（2）：102-107.

［5］张棋，贾方秀，殷婷婷.基于改进Sobel算法的实时图像边缘检测系统设计［J］.仪表技术与传感器，2018（2）：101-104，108.

［6］叶惠娇，冉全，成果.FPGA图像边缘检测系统的设计与实现［J］.计算机应用与软件，2018（12）：237-240，302.

［7］谭媛，黄辉先，徐建闽，等.基于改进Sobel算子的遥感图像道路边缘检测方法［J］.国土资源遥感，2016（3）：7-11.

［8］SUDHARSHAN K M.Design of a Sobel Edge Detection Algorithm on FPGA［J］.Turkish Journal of Computer and Mathematics Education（TURCOMAT），2021（12）：2458-2462.

［9］陳鑫元，李筠，杨海马，等.自适应阈值图像二值化及形态学处理的FPGA实现［J］.电子测量技术，2016（7）：67-71.

（编辑 王永超）

Implementation of multidirectional threshold adaptive Sobel algorithm based on FPGA

Cheng Weitao， Guo Laigong， Wang Qiang

（School of Electrical and Information Engineering，Anhui University of Science and Technology， Huainan 232001， China）

Abstract： Sobel edge detection technology is one of the most basic technologies in image processing. The traditional algorithm is slow and has only two gradients in the vertical and horizontal directions. The effect of edge detection in some other directions is not obvious. This paper designs a four-direction （0°， 45°， 90°， 135°） Sobel algorithm to improve the accuracy of edge detection. Aiming at the defect that the threshold setting of the traditional Sobel edge detection algorithm may deviate， based on median filtering， adaptive algorithm is adopted to improve the accuracy of the threshold. The design is programmed in Verilog language. The simulation results show that the multi-directional threshold adaptive Sobel processing speed is fast， the adaptive threshold is reasonable， and the integrity of the edge is significantly improved than the traditional method.

Key words： Sobel; adaptive threshold; FPGA; MATLAB