基于偏振补偿的级联式液晶偏振光栅衍射效率优化方法

胡 虎，刘雪莲，王春阳，*，王子硕，梁书宁

（1. 西安工业大学 兵器科学与技术学院，陕西 西安 710021；2. 西安工业大学 西安市主动光电成像探测技术重点实验室，陕西 西安 710021；3. 长春理工大学 电子信息工程学院，吉林 长春 130022）

1 引 言

液晶偏振光栅（Liquid Crystal Polarization Grating，LCPG）是一种新型的高衍射效率、超薄型、可实现非机械式光束偏转的液晶器件，其基于几何相位来调制入射光的偏振态，进而控制出射光的偏转级次。由于液晶偏振光栅具有小型化、轻薄化、灵敏度高等优点［1-3］，在激光雷达、激光通信、扫描成像等领域应用广泛［4-8］。

液晶偏振光栅根据加电方式分为主动式与被动式。主动式液晶偏振光栅通过加电使液晶分子发生偏转，进而实现光束偏转。被动式液晶偏振光栅中的液晶分子取向已经固化，自身不加电，需要配合液晶电控波片（Liquid Crystal Cariable Retarder，LCVR）使用，实现光束偏转只取决于液晶电控波片所调制的入射光偏振态。

单个液晶偏振光栅和液晶电控波片构成的子系统只能实现固定的光束偏转角度。为提高光束偏转角度的范围和数量，需要将多个子系统交替排列形成级联式液晶偏振光栅［8-12］。国内外学者针对由多片液晶偏振光栅级联组成的级联系统开展了研究。Kim 等人将两个偏转度数分别为5°和10°液晶偏振光栅与半波片组合进行级联使用，在1 550 nm 下实现了5°分辨率、视场为-15°～+15°的离散扫描，并采用垂直入射下液晶偏振光栅的光栅方程计算衍射效率，范围为99.4%～99.6%［13］。Kim 等人介绍并对比了3 种不同级联方案的光束偏转角和系统透过率等参数，设计了一种可以实现31 个角度偏转、52°扫描视场角、衍射效率范围为92%～99%的4 级准三进制级联方案［14］。Kim 等人研究了4 种不同的级联方案，设计了一种5 级的超二进制级联方案，在1 064 nm 下实现了32 个角度的偏转，最大偏转角为40°，系统分辨率为2.6°，衍射效率最高达到了91%［15］。Kim 等人搭建了三进制级联方案的实验平台，实现了最大偏转角为65°、角度分辨率为8°的一维光束偏转系统，在入射波长为1 550 nm 的情况下，衍射效率总体达到了93%～96%［16］。Steven等人基于二进制级联方案实现了二维扫描，系统的最大偏转角为64°，分辨率为3.2°，衍射效率最低为80%［17］。

综上所述，目前的研究重点在于将液晶偏振光栅进行级联使用来提高光束偏转角度的范围，并且计算级联系统衍射效率的方法均为垂直入射下的光栅方程，并未考虑级联系统中的斜入射会改变椭圆率和液晶电控波片工作电压的问题。本文将扩展琼斯矩阵、斯托克斯参数、矢量衍射理论三者结合，建立了级联式液晶偏振光栅衍射模型。利用该模型可以定量计算级联系统在不同偏转角度下的衍射效率。通过求解液晶分子指向矢和计算斜入射下液晶电控波片相位延迟，推导液晶电控波片相位延迟与椭圆率的关系，计算液晶电控波片的最优工作电压并对其进行优化，实现对斜入射造成退偏量的偏振补偿，提升了级联系统的衍射效率。

2 液晶偏振光栅级联方案设计与衍射模型

2.1 液晶偏振光栅级联方案设计

液晶偏振光栅由3部分组成：液晶分子（Liquid Crystal，LC）、取向层以及玻璃基板。液晶分子多层旋涂在具有取向层的玻璃基板上，其基本结构如图1 所示。液晶偏振光栅中的液晶分子呈周期性排列，其长轴方向在一个周期内在0～π 不断变化，并且在x=0 和x=Λ处，液晶分子双折射率相同。

图1 LCPG 基本结构图Fig.1 Basic structure diagram of LCPG

液晶电控波片由光控取向层（Linearly Polarized Photo-polymerization，LPP）、玻璃基板、氧化铟锡薄膜层（Indium Tin Oxide film，ITO）和液晶分子组成。液晶电控波片中的液晶分子具有电光效应，外加电压发生改变时，液晶分子将重新定向。液晶电控波片未施加电压时的液晶分子排列图如图2（a）所示，施加电压时的液晶分子排列图如图2（b）所示。

图2 （a）未施加电压下液晶分子排列图；（b）施加电压下液晶分子排列图。Fig.2 （a） Molecular arrangement of liquid crystal without applied voltage；（b） Molecular arrangement diagram of liquid crystal under applied voltage.

本文采用一种二进制液晶偏振光栅级联方案，该方案由4 个液晶电控波片和液晶偏振光栅构成的子系统堆叠而成，且4 片液晶偏振光栅的最大偏转角分别为0.33°、0.67°、1.33°和2.67°。基于二进制液晶偏振光栅级联方案能实现的最大光束偏转范围θmax、总偏转角个数Ω、液晶器件个数M、液晶偏振光栅个数N和系统分辨率α的关系表达式如式（1）～（3）所示：

当光束垂直入射时，液晶偏振光栅衍射效率最高。但在实际级联系统中，入射光在通过第一片液晶偏振光栅发生偏转后，会带有偏转角度倾斜入射到后面的光栅。图3 为光束在级联式液晶偏振光栅中产生的斜入射示意图。

图3 光束在级联式液晶偏振光栅中产生的斜入射示意图Fig.3 Schematic diagram of oblique incidence of light beam in cascaded liquid crystal polarization gratings

2.2 级联式液晶偏振光栅衍射模型

当光束斜入射进入液晶偏振光栅时，需要使用扩展琼斯矩阵来表征光束在液晶偏振光栅中的传输过程［18-22］。斜入射会改变液晶分子倾斜角，进而造成折射率的不同，导致相位延迟量发生改变。为分析斜入射角度对液晶偏振光栅相位延迟的影响，建立了如图4 所示的三维空间坐标系。

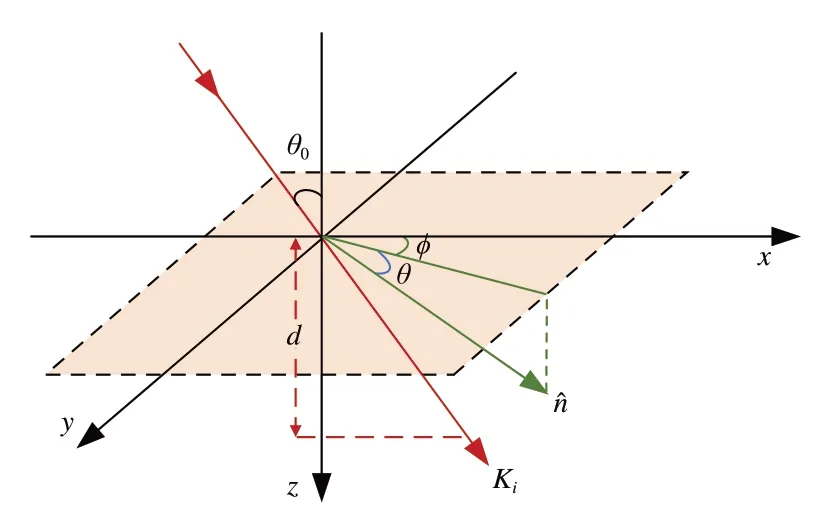
图4 液晶分子指向矢与入射光矢量的三维坐标图Fig.4 Three-dimensional coordinate diagram of LC director and incident beam vector

图4 中，Ki为入射光矢量，θ0为斜入射角度，n^为液晶分子指向矢，θ为液晶分子倾斜角，φ为液晶分子方位角。根据图4 可得此时e 光和o 光投影到z轴的分量为：

由图4 可知，光束斜入射进入液晶层时，入射光的光程不再为液晶盒厚度d。斜入射时通过液晶层光束的光程如式（6）所示：

结合式（4）、（5）、（6）可以求出光束斜入射时通过液晶偏振光栅的相位延迟：

由图4 可知，将液晶偏振光栅沿x轴分成N层，再假设在任意单层之间均存在可忽略厚度的各向同性介质。当分层数目足够多时，任意单层都能够等同于独立的单轴晶体。因此，其拓展琼斯矩阵可以表征为［20］：

视各向同性介质的折射率为no，由于o 光方向始终垂直于光轴并且液晶分子的n∥和n⊥数值差距不大，因此只使用液晶盒参数和斜入射角度就可以求解拓展琼斯矩阵。基于上述分析将Jn化简为式（9）：

其中：Δ=cosφcosθncosθo-sinθnsinθo，B=(1-eiΓ)。

根据上述理论推导，可以求解出N层液晶偏振光栅总的琼斯矩阵为：

液晶电控波片的琼斯矩阵为［23］：

式（11）中的δ为液晶电控波片的相位延迟：

设子系统入射光的琼斯矩阵为Ein，则出射光的琼斯矩阵为：

在级联系统中，当光束经过第一片液晶电控波片并入射到第一片液晶偏振光栅后，出射光的琼斯矩阵Eout_k+1为：

其中，k=1，2，3，4 为不同偏转角度的液晶偏振光栅序号。由于多片光栅级联，前一片光栅的出射光经液晶电控波片后，为后一片光栅的入射光束，如式（15）所示：

由矢量衍射理论可知［24］，出射光束的琼斯矩阵的矢量傅里叶系数决定m级次的衍射效率。因此，后面级联的光栅m级次的出射光束傅里叶变换系数为：

式中：Λ是光栅周期，T和K分别是光栅和液晶电控波片的琼斯矩阵。

液晶偏振光栅的m级衍射效率为m级衍射光束与总衍射光束的对应能量之比，并且m级衍射光束的能量与|Dm_k+1|2成正比例关系。因此第m级的衍射效率可以表征为：

级联系统的总衍射效率为系统中每一个子系统衍射效率的乘积：

由式（18）即可定量计算出级联系统偏转至不同角度时的衍射效率。

3 斜入射下液晶电控波片的相位延迟

液晶电控波片中的液晶分子具有介电各向异性，可以通过调节外加电压来改变液晶分子指向矢分布。液晶分子指向矢的方向为单位体积内液晶分子的平均指向，其数学表达式如式（19）所示：

式中，θ和φ分别为液晶分子的倾斜角与方位角。在液晶分子趋于平衡状态的过程中，自由能密度为最小。根据连续体弹性形变理论，将吉布斯自由能方程与式（19）相结合，可以求解出系统总的自由能密度：

式中：m(θ) = (K11cos2θ+K33sin2θ)；g(θ，φ)=cos2θ(K11sin2φ+K22cos2φsin2θ+K33cos2φcos2θ) ；h(θ，φ)=K22cos2θsinφ-K11cos2θsinφ；K11为展曲系数，K22为扭曲系数，K33为弯曲系数。

根据变分原理可知，当液晶分子处于平衡状态时，系统总自由能的变分δF=0。结合欧拉公式，将式（20）所示的变分问题化简为3 个偏微分方程：

采用差分迭代法对式（21）、（22）、（23）进行求解，可以计算出外加电压与液晶分子倾斜角的关系。本文分析的器件所用均是向列相液晶材料，其弹性系数为K11=11.1×10-12N，K22=7.4×10-12N，K33=17.1×10-12N；介电常数为ε0=8.854×10-12F m，ε∥=19.0ε0，ε⊥=5.2ε0；折射率为n0=1.521，ne=1.746；液晶盒厚度d=5×10-6m；激光波长为λ=1 064×10-6m。根据上述参数仿真不同电压下的指向矢分布，得到电压与液晶分子倾斜角的关系如图5 所示。

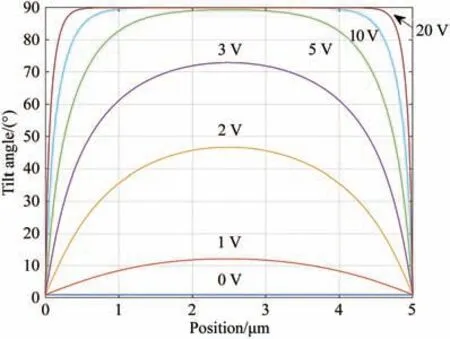
图5 液晶分子倾斜角与电压的关系Fig.5 Relationship between liquid crystal molecular tilt angle and voltage

由图5可以看出，电压和位置均会造成液晶分子倾斜角发生改变。由于液晶分子会受到基板的强锚定作用，因此靠近基板处的倾斜角趋近于0。

为分析斜入射下液晶电控波片的相位延迟特性，建立如图6 所示的坐标系［25］。图6 中，xyz坐标系是根据液晶电控波片的正入射光平面及其法线建立，xOy平面平行于入射光法平面，z轴平行于该平面的法线。XYZ坐标系则是根据竖直方向和斜入射光束的方向建立，X轴与x轴重合，Z轴与斜入射光束的反方向重合。OQ表示液晶分子指向矢的方向，OQ1和OQ2是指向矢的方向在XOY和xOy平面上的投影。

图6 斜入射下液晶电控波片的内部结构图Fig.6 Internal structure diagram of liquid crystal variable retarder under oblique incidence

图7 描述了当光束以斜入射角度θ0入射液晶电控波片时的折射现象。根据折射定律，可以得到斜入射角θ0与折射角ρ的关系：

其中n是液晶在当前入射光波长下的折射率。光束经过液晶层的光程为：

根据图6，可以得到液晶分子倾斜角θ和入射光的夹角α间的关系［25］：

同时根据图中几何关系可知：

因此OQ1与液晶分子指向矢之间的夹角θ'可以表示为：

联立式（12）及式（24）～（28），得到斜入射下液晶电控波片的相位延迟为：

图8 为根据式（29）计算出的在1 064 nm 波长下，斜入射角度分别为0°、+5°和+10°，外加电压在0～20 V 范围内，同时其方位角为10°的液晶电控波片相位延迟特性图。从图8 可以看出，斜入射角度和电压会影响液晶电控波片的相位延迟。

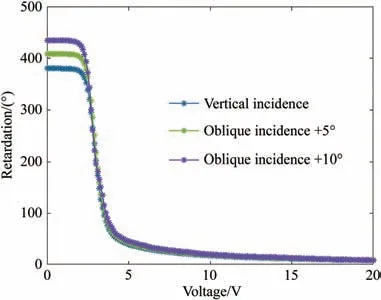
图8 斜入射角度、电压和相位延迟的关系。Fig.8 Relationship between oblique incident angle，voltage and retardation.

4 级联式液晶偏振光栅衍射效率的优化

4.1 椭圆率对衍射效率的影响

将出射光的拓展琼斯矩阵Eout_k与斯托克斯参数结合，可以计算出射光的椭圆率：

其中：I0为入射光的总光强，S3表示圆偏振的分量，χ表示椭圆率，、分别为x方向上的光矢量及其复共轭，y方向同理。当光束斜入射角度在±10°范围内入射2.67°的液晶偏振光栅时，出射光椭圆率的变化如图9 所示。由图9 可知，斜入射角度越大，出射光的椭圆率越小。椭圆率在0°～45°范围内的光束垂直入射2.67°的液晶偏振光栅时，衍射效率的变化如图10 所示。由图10可知，入射光的椭圆率会影响液晶偏振光栅的衍射效率。

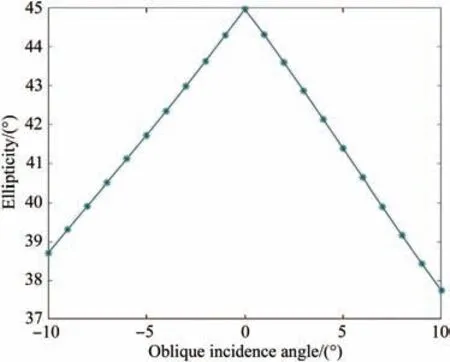
图9 斜入射角度与椭圆率的关系Fig.9 Relationship between oblique incidence angle and ellipticity

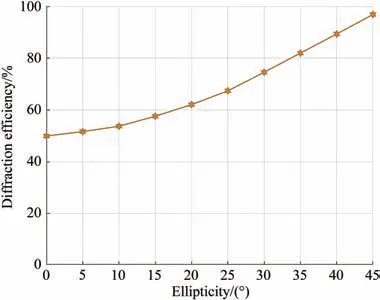
图10 入射光椭圆率与衍射效率的关系Fig.10 Relationship between ellipticity of incident light and diffraction efficiency

4.2 斜入射角度对衍射效率的影响

结合式（13）、（16）、（17）、（32），仿真出斜入射角度在0°～+20°范围内入射2.67°的液晶偏振光栅时的出射光束椭圆率与衍射效率的关系，如图11 所示。从图11 可以看出，随着倾斜角度的增大，出射光束的椭圆率逐渐减小，衍射效率逐渐降低。

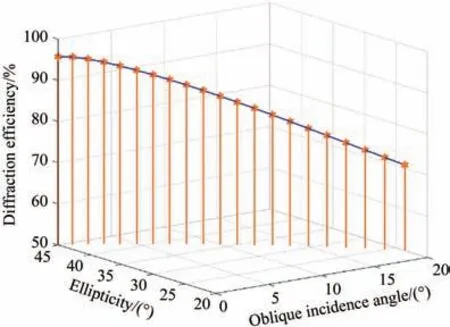
图11 斜入射角度、椭圆率与衍射效率的关系。Fig.11 Relationship between oblique incident angle，ellipticity and diffraction efficiency.

综上分析，级联式液晶偏振光栅中的斜入射现象会影响衍射效率。分析建立的级联式液晶偏振光栅衍射模型可知，通过计算液晶电控波片的最优工作电压并对其进行优化，可以改变其相位延迟δ补偿斜入射造成的退偏量，实现级联系统衍射效率的提高。

通过斯托克斯参数求解相位延迟δ与椭圆率χ的关系，可以计算出不同斜入射角度下液晶电控波片的最优工作电压。

5 测量实验与结果

5.1 斜入射下液晶电控波片的相位延迟

本文基于1/4 波片法来测量斜入射下液晶电控波片的相位延迟［26］，实验示意图如图12（a）所示，实验光路如图12（b）所示。系统由10 64 nm激光器、光电探测器、偏振片A1、偏振片A2、λ/4波片和液晶电控波片构成。

图12 （a）实验示意图；（b）实验装置图。Fig.12 （a） Schematic diagram of experiment； （b） Diagram of experimental device.

斜入射角度分别取0°、+5°和+10°，给液晶电控波片施加不同电压，使用光电探测器测量其相位延迟的变化［26］，测量结果如图13 所示。

图13 斜入射角度、电压和相位延迟的关系。Fig.13 Relationship between oblique incident angle，voltageand retardation.

从图13 可以看出，驱动电压超出液晶电控波片阈值电压时，相位延迟和电压呈现反比例关系。驱动电压一定时，相位延迟量随着斜入射角度的增大而增大。

5.2 椭圆率对衍射效率的影响

为验证光束斜入射进入液晶偏振光栅时会改变出射光的椭圆率，本文搭建了如图14 所示的实验平台。实验装置包括1 064 nm 激光器、λ/4波片、偏振片、液晶偏振光栅、偏振态测量仪。

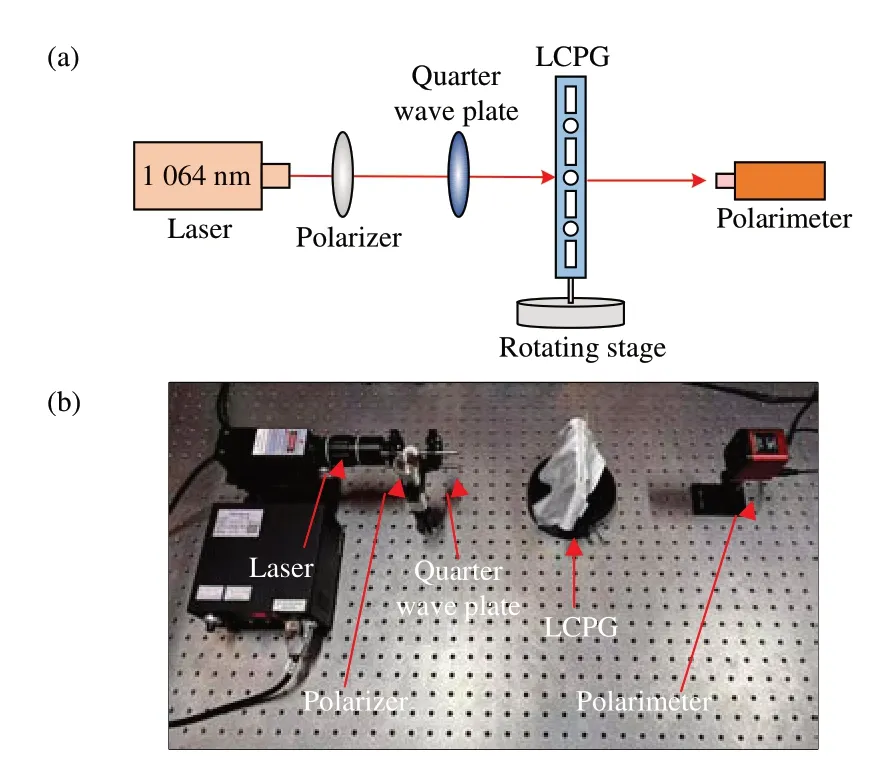
图14 （a）实验示意图；（b）实验装置图。Fig.14 （a） Schematic diagram of experiment； （b） Diagram of experimental device.

利用偏振态测量仪测量不同斜入射角度下液晶偏振光栅出射光的椭圆率。当光束斜入射角度在±10°范围内进入液晶偏振光栅时，测量结果如图15 所示。

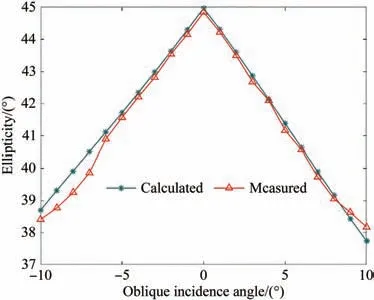
图15 斜入射角度与椭圆率的关系Fig.15 Relationship between oblique incidence angle and ellipticity

为验证入射光的椭圆率会影响液晶偏振光栅的衍射效率，利用CCD 相机采集不同椭圆率下出射光斑图案，见图16。可以看出，入射光为45°椭圆率时，光束完全偏转至+1 级；入射光为15°椭圆率时，-1 级的能量逐渐增强；入射光为0°椭圆率时，+1 级和-1 级的能量各占50%。

图16 （a）椭圆率45°的入射光斑图；（b）椭圆率15°的入射光斑图；（c）椭圆率0°的入射光斑图。Fig.16 （a） Light spot pattern at 45° ellipticity；（b） Light spot pattern at 15° ellipticity； （c） Light spot pattern at 0° ellipticity.

5.3 斜入射角度对衍射效率的影响

为验证光束斜入射进入液晶偏振光栅会影响衍射效率，本文搭建了如图17 所示的实验平台。实验装置包括偏振片、1064nm 激光器、λ/4波片、液晶偏振光栅、CCD 相机和光屏。

图17 （a）实验示意图；（b）实验装置图。Fig.17 （a） Schematic diagram of experiment； （b） Diagram of experimental device.

利用CCD 相机采集不同入射角度下液晶偏振光栅出射光的光斑图案如图18 所示。从图18可以发现，光束垂直入射时，出射光完全偏转至+1 级，不存在+1 级光束能量的损失，此时衍射效率最高。当斜入射角度从5°增大为10°时，衍射0级光斑逐渐变亮，出现漏光现象。而0 级衍射效率的升高，会影响+1级的衍射效率。

图18 （a） 0°入射下光斑图；（b）+5°入射下光斑图；（c）+10°入射下光斑图。Fig.18 （a） Light spot pattern at 0° incidence； （b） Light spot pattern at 5° incidence； （c） Light spot pattern at 10° incidence.

5.4 级联式液晶偏振光栅衍射效率优化

为验证所提方法对级联式液晶偏振光栅衍射效率优化的有效性，本文搭建了如图19 所示的实验平台。实验装置包括1 064 nm 激光器、偏振片、λ/4 波片、最大转向角为±5°的级联式液晶偏振光栅和能量计等。级联式液晶偏振光栅是由液晶电控波片和液晶偏振光栅的组合堆叠而成，在本实验中各有4 片。

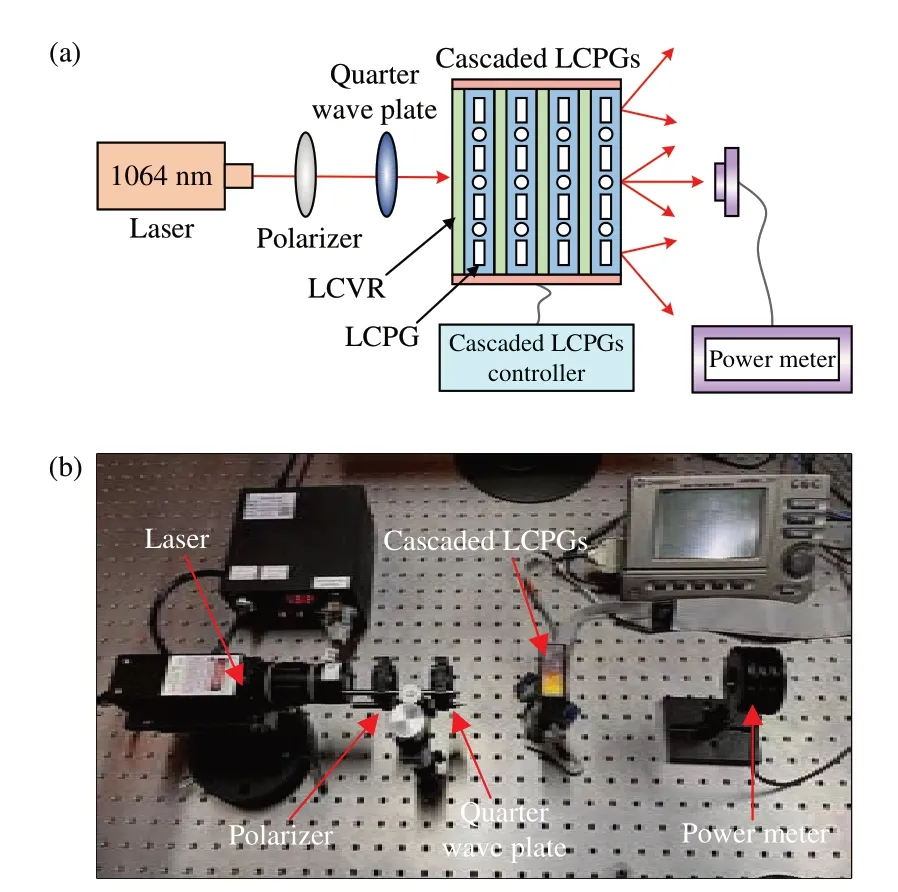
图19 （a）实验示意图；（b）实验装置图。Fig.19 （a） Schematic diagram of experiment； （b） Diagram of experimental device.

结合公式（29）、（32）、（33），可以计算出不同斜入射角度下液晶电控波片的最优工作电压，如图20 所示。

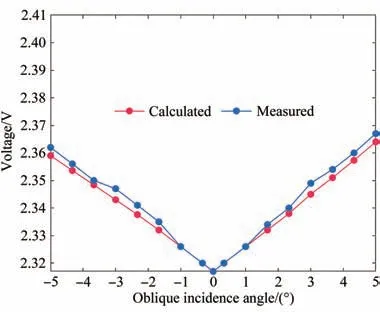
图20 斜入射角度与LCVR 最优工作电压的关系Fig.20 Relationship between oblique incidence angle and optimal operating voltage of LCVR

计算出液晶电控波片最优工作电压后，通过上位机软件控制驱动电路，对级联系统中液晶电控波片的工作电压进行优化。使用CCD 相机采集级联系统光束偏转至+3.67°时的液晶电控波片电压优化前后的光斑图案，如图21 所示。

图21 （a）电压优化前光斑图；（b）电压优化后光斑图。Fig.21 （a） Spot diagram before voltage optimization；（b） Spot diagram after voltage optimization.

从图21 可以看出，光束偏转到+3.67°时，由于斜入射的影响，出现了杂散光，导致液晶电控波片的最优工作电压发生改变。当优化级联系统中的液晶电控波片电压后，杂散光明显减少，实现了衍射效率的提高。

基于所建立的级联式液晶偏振光栅衍射模型，可以定量计算出级联系统在不同偏转角度下的液晶电控波片工作电压优化前后的衍射效率。利用能量计记录级联系统衍射效率随光束偏转角度以及液晶电控波片工作电压优化前后的数据，结果如图22 所示。由图22 可以看出，级联系统的衍射效率随系统偏转角度而变化，最大下降了约3%。当优化液晶电控波片的工作电压后，级联系统整体衍射效率最高提升了4%左右。由衍射效率变化趋势可知，级联系统的衍射效率呈现中间低、两边高分布。

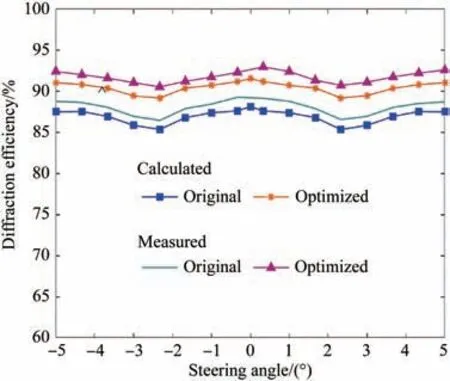
图22 级联系统电压优化前后在不同偏转角度下的衍射效率Fig.22 Diffraction efficiency diagram of cascade system with different steering angles before and after voltage optimization

6 结 论

本文从液晶偏振光栅的基本理论出发，设计了液晶偏振光栅级联方案，建立了级联式液晶偏振光栅衍射模型，求解了斜入射下液晶电控波片的相位延迟，计算了液晶电控波片的最优工作电压，优化了级联系统的衍射效率。仿真和实验结果表明，斜入射会改变椭圆率从而影响光束衍射效率。斜入射角度越大，液晶偏振光栅出射光的椭圆率越小，衍射效率越低。级联系统光束偏转角度角从-5°偏转到+5°时，衍射效率最大下降了3%。优化液晶电控波片工作电压后，衍射效率整体提升了3%～4%。因此，在实际应用环境下，为实现高衍射效率的光束偏转，应及时更新液晶电控波片的工作电压，避免因为工作电压改变导致系统衍射效率的下降。