纵向风下隧道火灾顶部排烟烟气温度分布研究
徐梦一 袁中原
(西南交通大学机械工程学院 成都 610031)
0 引言
隧道因其特殊的管状封闭结构,在发生火灾时常伴随着高温、能见度低、排烟困难,会造成逃生疏散困难,隧道结构严重破坏等后果[1,2]。通过设计一个合理的排烟系统,能够及时有效地降低烟气温度并控制烟气蔓延及沉降,对于减轻人员伤亡和财产损失尤为重要。
纵向通风系统可在着火点上游方向形成无烟疏散通道,便于人员逃生,且能够有效降低隧道内温度,建造和运维成本低,但容易出现风流紊乱的现象,能见度低,影响逃生救援;而半横向排烟系统能及时地将烟气排出隧道,有效控制烟气蔓延,但其建造复杂,造价和运维成本较高。近年来随着隧道排烟技术的发展,纵向通风和顶部排烟系统协同作用下的耦合系统广受关注,其综合了两种排烟方式的优点,使得排烟效果更好,又相对降低了成本。
目前,对于纵向通风和顶部排烟协同作用下的排烟系统,一些学者已经进行了初步研究[3-5]。Ingason 和Li[6]进行了小尺寸试验,研究了在有无纵向风情况下单个排烟口和两个排烟口的顶部排烟系统对于大型货车火灾烟气的控制作用。陈龙飞等[7]推导了排烟口位于火源上方的顶部排烟系统同纵向通风系统共同作用下的回流烟气长度预测数学模型,并进行了小尺寸试验验证其准确性;唐飞等[8,9]发现火源和顶棚排烟口的相对方向对烟锋流速有较大影响,当火源位于顶棚排烟口正下方时,机械排烟系统对烟气前缘速度的影响最为显著,并且在一定的无量纲放热速率下,临界流速随吊顶集中机械排烟流量的增大而减小;王明年等[10]通过采用试验和数值模拟相结合的方法,研究了不同排烟策略(改变纵向风速和排烟风速)对纵向风下的竖井排烟系统的影响,并给出了两种火源位置下的速度拟合公式。
然而,对于纵向通风和顶部排烟协同作用下不同因素对烟气分布特性的影响研究较少,本文采用火灾数值模拟软件FDS 对该系统的烟气分布特性进行了研究。
1 数值模拟
本文选取某山岭隧道建立几何模型,如图1 所示,隧道断面上部取半径6m 的半圆,下部取高为1.4m 矩形,模拟隧道总长取为500m,隧道宽12m,高7.4m。排烟口位于隧道顶棚中轴线上,其内边缘距隧道入口320m,宽为5m,设置了五种不同的风口长度:1m、5m、7m、10m、15m。在隧道纵向中轴线上设置了纵向温度测点和CO浓度测点及其切片,间隔为10m;在排烟口与隧道交界面处设置速度测点,用于监测排烟变化情况。
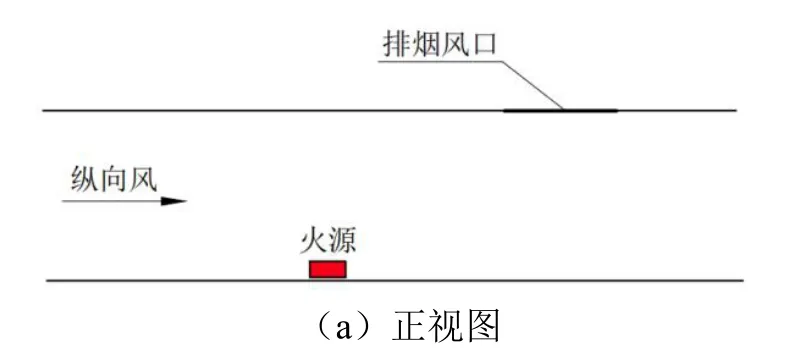
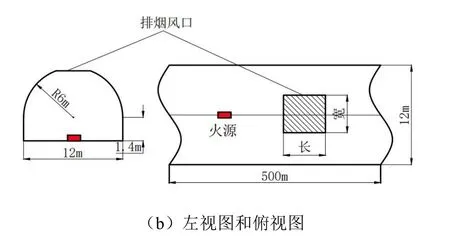
图1 模型隧道示意图Fig.1 The picture of tunnel model
本文选取5MW、10MW、30MW 三种火源热释放率进行数值模拟研究,总模拟时间为600s。隧道壁面的材料设置为“concrete”,厚度为0.5m,环境初始温度设置为25℃。本文研究的是纵向风下的隧道火灾排烟,在隧道入口与隧道交界面处设置“supply”,向隧道内送风,风速设为临界风速;在隧道出口与计算区域边界处设置为开口条件。隧道火灾数值模型如图2 所示。
图2 数值模型示意图Fig.2 The picture of the numerical model
将火源设置在隧道纵向中轴线上,火源与排烟风口的相对位置如图3 所示,其中A 位置位于隧道纵向中心,B 位置距排烟风口处500m,C 位置距排烟风口处1000m。
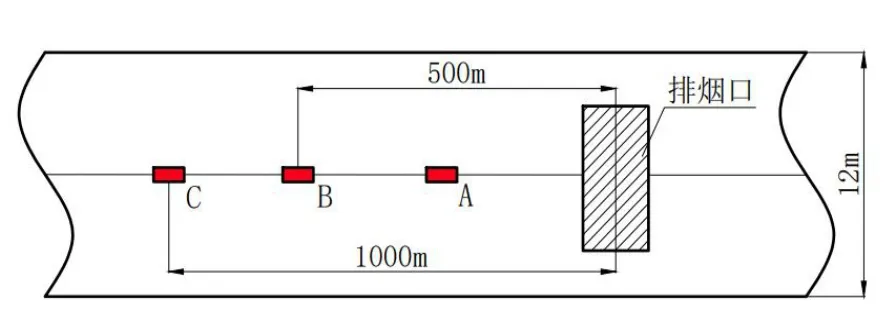
图3 火源位置示意图Fig.3 The picture of fire source position
为研究纵向风下的隧道火灾顶部排烟系统烟气特性分布与纵向火源位置、排烟口长度、排烟量和火源热释放率之间的关系,本文共设计了30 组数值模拟工况,如表1 所示。

表1 数值模拟工况Table 1 Numerical simulation of the operating conditions
本文开展了1:10 缩尺模型隧道试验,选取火源热释放率为5.68kW,排烟量为180m3/h 的典型试验工况验证了本文数值模型的准确性,如图4 所示,数值模拟计算结果与试验结果基本吻合,可用于模拟计算隧道火灾。
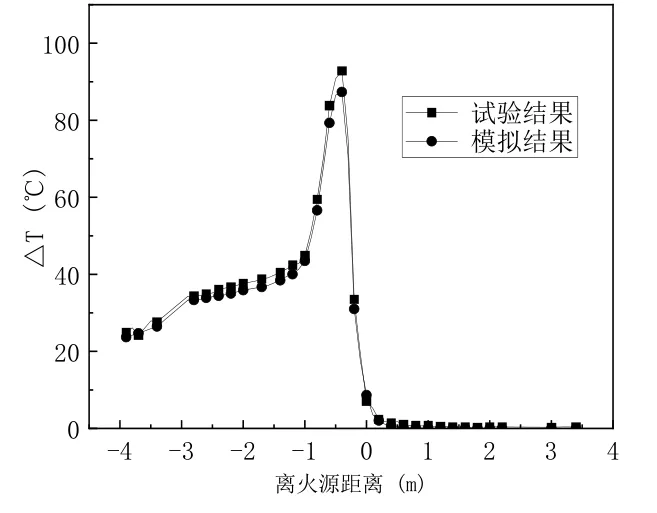
图4 数值模拟验证结果Fig.4 The result of the numerical simulation verification
为了便于分析和说明,定义火源到排烟口之间的区域为火源段,排烟口之外的区域为非火源段。
2 烟气特性
2.1 烟气分布规律
图5 为在纵向风速为临界风速时,排烟风口长度为6m,排烟量为120m3/s 时的烟气分布特性。其中横坐标表示点离开火源的距离,单位为m,纵坐标表示热电偶测得的温度与室内温度的温差,单位为℃。以风机向隧道内送风的方向为“﹢”,火源位于横坐标为“0”处,图中温度突变处为风口所在位置。

图5 隧道顶壁烟气特性分布Fig.5 The smoke characteristics distribution of tunnel beneath ceiling
从图5(a)中可以看出,隧道顶壁烟气温度在离火源20m 距离处达到最大,并在沿隧道纵向扩散过程中逐渐减小,在风口处有明显的突变。这是由于纵向风的作用,使得火源向下风方向倾斜,当风速达到临界风速时,通风抑制烟气向火源上游的扩散,回流长度为0,此时顶壁最高温度位置偏离火源上方,火源上游几乎无烟气扩散;随着烟气在火源段扩散,热烟气不断卷吸冷空气并与隧道壁面换热,烟气温度下降;当烟气扩散到风口下方时,在顶部排烟的作用下,大量的烟气被直接排出隧道,排烟口处温度急剧下降,越过排烟口的烟气继续沿隧道纵向扩散,温度进一步降低;最终烟气浮升力与进入隧道的新鲜空气的惯性力相等,烟气停止向前扩散。
而火源上游的温度衰减速度明显比下游衰减快。这是由于纵向通风,使得火源上游的空气与烟气流动方向相反,这对烟气流动产生阻碍作用,增加了隧道空间内的热对流,且烟气在沿隧道流动的过程中不断地与隧道壁面传热并不断卷吸周围的冷空气,温度进一步降低,因此火源上游的温度衰减相对更快。
从图5(b)中可以看出,火源附近的CO 浓度较高,在沿隧道纵向扩散的过程中烟气不断卷吸冷空气,烟气浓度降低,CO 浓度减小;随后由于大量烟气从风口排出,风口处CO 浓度骤减,其余烟气绕过风口继续向前扩散,CO 浓度降低;最终,烟气浮升力与进入隧道的新鲜空气的惯性力相等,烟气不再向前扩散。
2.2 纵向火源位置对烟气温度分布的影响
以火源功率为5MW,风口长度为7m,排烟量为120m3/s 的工况为例,图6 展示了不同纵向火源位置下隧道顶壁纵向烟气分布的情况。可以看出,火源段内,烟气温度沿隧道纵向方向逐渐降低,A、B、C 三个位置下的烟气纵向温度分布几乎一致,火源位置的改变不会明显影响顶壁烟气纵向温度分布。这说明由排烟引起的隧道补风气流的增加不会影响火源段的空气卷吸。而当烟气扩散至风口附近时,火源位于C 位置时的温度相对较低,A 位置时的风口下方温度相对较高。这是因为随着离火源距离的增大,热烟气在蔓延过程中与冷空气和隧道壁面不断换热,温度降低,火源位置与风口间距越大,烟气蔓延距离越长,温度下降得越多。
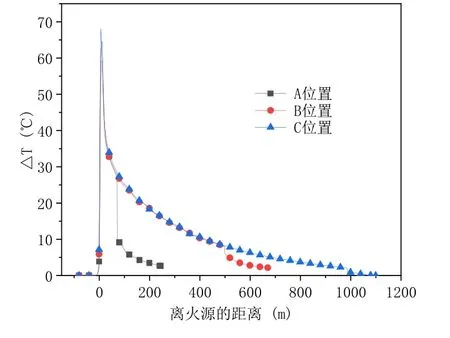
图6 纵向火源位置对温度分布的影响Fig.6 Effect of the longitudinal fire source location on smoke temperature distribution
2.3 排烟口长度对烟气温度分布的影响
图7 为火源热释放率分别为5MW 和10MW时,不同排烟风口长度对顶壁纵向烟气温度分布的影响。从图中可以看出,在排烟量一定的情况下,无论是火源段还是非火源段,在排烟口长度为1-15m 区间时的顶部烟气温度分布几乎都没有区别,由此可以判断出排烟风口尺寸不会对隧道顶部的烟气温度造成影响。

图7 排烟口尺寸对烟气温度分布的影响Fig.7 Effect of exhaust vent size on smoke temperature distribution
2.4 排烟量对烟气温度分布的影响
图8 为不同排烟量对顶壁烟气纵向温度分布的影响。从图中可以看出,在火源段,风口的排烟情况不会影响到火源段的顶壁温度分布;而在非火源段,烟气的顶部温度会随着排烟量的增加而上升。这是因为在纵向风速一定时,排烟风量增大,隧道内负压增加,导致隧道口的补风气流大部分从排烟口排出或直接排出隧道,几乎不会流入火源段,火源段烟气的卷吸几乎不受到由排烟引起的补风气流的影响。
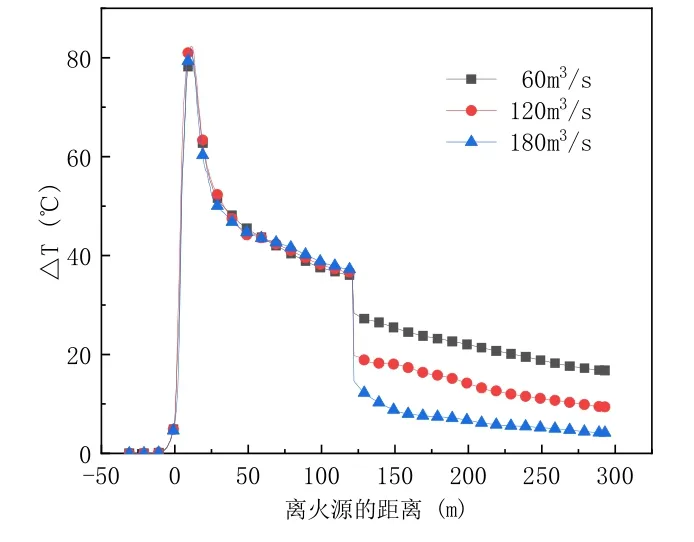
图8 排烟量对顶部纵向温度分布的影响Fig.8 Effect of smoke exhaust volume on smoke temperature distribution
2.5 火源功率对烟气温度分布的影响
图9 为不同火源功率对顶壁烟气纵向温度分布的影响。从图中可以看出,随着火源热释放率的增大,隧道内相同位置处的顶部烟气温度也随之增加。这是因为火源热释放率越大,释放的热量越多,火源上方的烟气温度就越高;而在离火源距离增加时,和其他因素的规律相同,随着烟气扩散时与隧道壁面换热,顶壁温度逐渐降低。
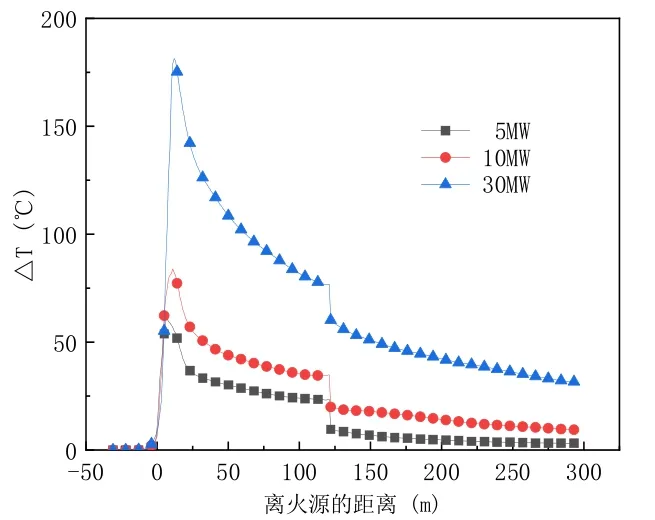
图9 火源功率对顶部纵向温度分布的影响Fig.9 Effect of fire source heat release rate on smoke temperature distribution
3 烟气温度纵向衰减
通过以上研究,表明在相同火源条件下,纵向火源位置、排烟口长度和排烟量在火源段的顶壁温升几乎一致,随离火源距离的增加,火源下游烟气温度呈指数函数衰减。根据胡隆华等[11]的研究分析得出了隧道顶棚无量纲烟气衰减模型,见式(1)。
式中:k为常数;ΔT为某纵向位置处温升,℃;ΔTref是参考位置温升,℃;x为与火源之间的距离;xref为参考位置与火源之间的距离。
Fan和Ji等[12]研究得到了隧道顶棚纵向温度的衰减公式。
式中:α,k、y0均为常数。
参考位置选取火源段顶壁烟气最高温度位置处,则无量纲烟气温升模型可以表示为:
由于风口处温度变化浮动较大,且风口下游的温度满足人员安全逃生要求,本文只对火源上方最高温度位置至风口位置处的顶壁纵向温度进行拟合。利用式(1)纵向温度衰减模型对本文烟气温度进行拟合,其拟合度系数小于0.80,说明胡隆华的烟气衰减温度模型不能很好的预测纵向通风和顶部排烟协同作用下的隧道火灾烟气温度分布。利用式(2)对不同风口长度下隧道火源段的无量纲烟气温度进行拟合,拟合曲线如图10 所示,得到k值为0.838,相关系数大于0.95,可以说明Fan和Ji 等的模型能很好地预测纵向通风和顶部排烟协同作用下的隧道火灾烟气温度分布。通过对参考位置处的试验数据取平均值,得出参考位置处的无量纲烟气温升=2.034,无量纲温升的定义如式(4)。
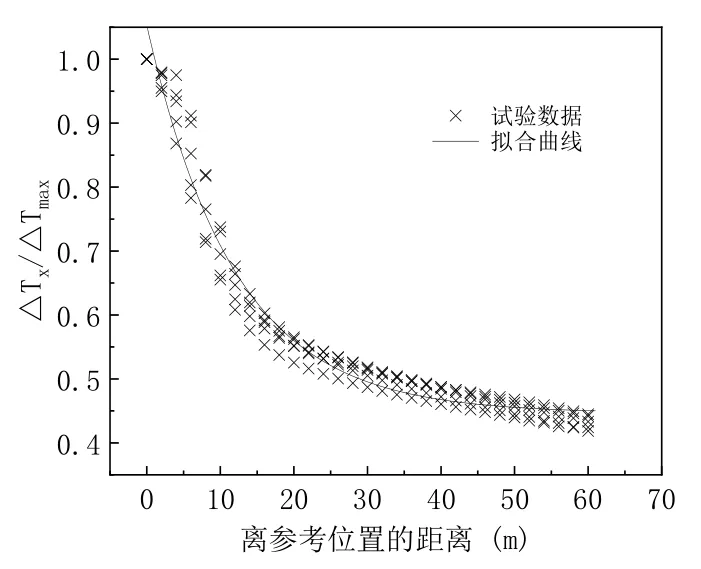
图10 火源段纵向温度衰减Fig.10 Longitudinal temperature decay of the fire source section
将公式(4)代入公式(3),得到公式(5),即为纵向通风和顶部排烟协同作用下的隧道火灾烟气温度计算模型:
式中:α=0.606,k=0.0838,y0=0.446。
图11 为不同纵向火源置下模拟计算所测温度与公式(5)计算所得温度对比图,可以看出公式(5)可以较好地表达不同火源位置下,不同风口长度顶壁下方纵向烟气温升的分布情况。
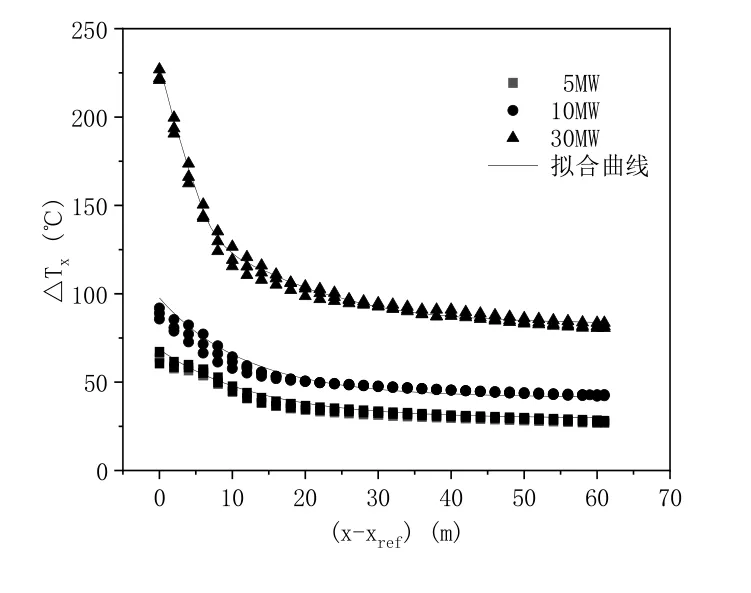
图11 公式(5)计算结果与模拟结果的对比Fig.11 Comparison between numerical simulation data and results predicted with Eq(5)
4 结论
(1)在纵向风和排烟口抽吸的作用下,隧道顶壁烟气温度随离火源距离的增大而逐渐减小,在风口处骤减,随后逐渐趋近室温。
(2)火源功率增加,火源段隧道顶壁烟气温度也随之增大,纵向火源位置、排烟口长度和排烟量对火源段隧道顶壁烟气温度几乎没有影响。
(3)通过Fan 和Ji 等建立的纵向温度衰减模型,得到了纵向风下隧道火灾顶部排烟系统内的顶壁下方无量纲烟气温度衰减模型。

