一种改进型KB-RLS算法在自适应干扰对消中的仿真分析

王铎澎,黄 华,张生凤

(中国船舶集团有限公司第八研究院,江苏 扬州 225101)

0 引 言

在日益恶劣的电子对抗环境中,现代一体化电子对抗平台在实际工作中不可避免地需要面对强自干扰导致的传输误码率增加、接收信噪比恶化乃至接收饱和系统自激等问题[1-2]。在针对收发系统间的强自干扰进行抑制的过程中,通常的抑制方法有3种:天线对消、射频对消和数字对消[3-7]。天线对消通过对系统收发天线的设计增加系统隔离度,进而对自干扰进行抑制,如文献[3]针对不同天线距离和不同信号频带,对不同传播模式下的天线对消效果进行了讨论。射频对消则是通过构造射频模拟电路,构造与干扰反相的信号来抵消干扰,在已有的研究中,如文献[4]在射频域,针对500 MHz的电磁信号,设计模拟抑制电路,取得22～40 dB的抑制效果。但是,收发系统间的强自干扰经过天线对消和射频对消后,虽然消除了自干扰信号中的主要部分,残余的多径成分与射频干扰抵消引入的非线性成分仍会影响期望信号的解调[5],还需要数字域干扰抑制技术进一步提升系统的自干扰抑制能力。数字域自干扰对消是指对AD采样后的数字信号进行对消处理,如文献[6]利用自干扰信道重建自干扰抑制的方法,通过自干扰信道估计和自干扰信号重建,在数字域最高取得了55 dB的干扰抑制效果。在整个自干扰对消的过程中,为了保证对强自干扰最终的抑制效果,如何在数字域这道最后的防线进行充分的对消,便具有极为重要的研究价值[7]。

目前已有的研究中,数字域自干扰对消技术主要有自干扰信道估计重建对消和自适应滤波对消方法2种[8-13]。自干扰信道估计重建对消主要是利用各类算法在时域或频域估计出自干扰信道后进行自干扰重建抵消;另一种数字域自适应滤波自干扰抑制则是通过在数字域对自干扰信号进行自适应滤波之后,进行自干扰抑制。文献[8]利用自干扰信道估计的方法在频域针对15 dB干噪比的莱斯噪声,取得最高22 dB的抑制效果。通过对文献[8]、[9]的对比分析得到,自干扰信道重建自干扰抑制方法虽然能取得较好的干扰抑制效果,但参考具体的算法流程,该方法较为复杂且运算参量较多,不适合工程实现,而目前已有的工程应用则主要是针对自适应滤波自干扰对消方法进行展开[10-13]。

在常见已有的自适应滤波自干扰对消算法研究中,自适应算法主要有递归最小二乘(RLS)算法和最小均方(LMS)算法2种,如文献[10]针对全双工单通道系统,利用LMS准则下的自适应滤波算法进行对消,取得了20 dB的自干扰抑制效果,但迭代速度缓慢,不满足电子对抗环境的时效要求。文献[11]利用经典的RLS算法进行了硬件层面的仿真测试,利用24阶的RLS滤波器取得了最大32.16 dB的抑制效果,未能达到预期的对消精度,同时该方案在硬件设计过程中,还有一定的优化空间。文献[12]则是对RLS算法的计算过程进行改进,利用搜索求解的办法,针对典型的莱斯噪声,进行对消测试。该方法虽然降低了RLS算法的求解复杂度,但同时也降低了RLS算法原有的对消精度。文献[13]则是利用正交三角(QR)分解的方法代替了RLS算法中矩阵求逆的过程,同时设计了Systolic脉动阵列进行仿真对消测试。该方法具有很好的收敛速度和收敛精度,但实际测试中,对信号的输入具有较高的要求,还需进一步的信号特征分析和算法改进。对上述研究[10-13]中的算法处理过程进行比较,得到LMS及改进算法。由于算法本身的特点,其收敛速度受到一定限制,不适合该场景下的工程应用。经典RLS及相关的改进算法虽然可以满足收敛速度的要求,但未兼顾算法复杂度、收敛精度、收敛速度、鲁棒性,对多种信号的适应性等工程实践的重要关注点,在实际的工程应用中仍不能取得较好的对消效果。

本文在考虑到已有各种自适应算法不足的前提下,对已有的RLS算法迭代过程进行具体讨论,并针对收发系统间的强自干扰提出一种新的改进型RLS算法。该RLS改进算法对算法迭代过程中的收敛因子和自相关矩阵的迭代计算过程进行改进,进而兼顾算法的收敛速度、鲁棒性等重要关注点,进一步提高了RLS算法在自干扰对消应用中的适应性和稳定性。

1 算法模型分析

对于常见的自适应滤波自干扰对消系统,系统主要结构如图1所示,发射干扰信号功分成2路:一路作为输入信号x(n)进入滤波器;一路作为参考信号d(n),经过整条发射链路后进入滤波器。输入信号拟合出重建信号y(n)后对参考信号进行抵消,最后达到抵消自干扰的目的。

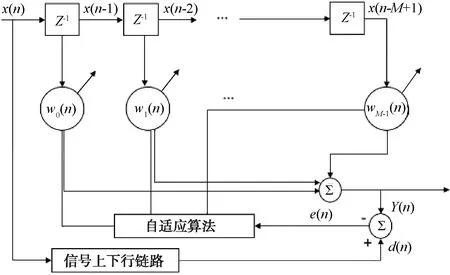
图1 自适应算法自适应滤波结构示意图

在该系统中,对于M阶RLS自适应滤波器,X(n)、W(n)是迭代开始前的输入信号向量和权值向量,该向量在首次迭代之前进行初始化:

X(n)=[x(n),x(n-1),…,x(n-M-1)]T

(1)

W(n)=[w0(n),w0(n),…,wM-1(n)]

(2)

迭代过程中,计算该次误差、卡尔曼增益向量和权值迭代系数,其中d(n)为对应的参考信号,λ为大于0小于1的遗忘因子:

e(n)=d(n)-WTX(n)

(3)

(4)

W(n)=W(n-1)+K(n)e(n)

(5)

式中:PMM是自相关信号的迭代矩阵,通常初始化为对角线的M阶单位矩阵,迭代计算公式为:

PMM(n-1)]

(6)

至此完成了整个RLS算法的迭代过程。对应的卡尔曼滤波结构中,代价函数为:

(7)

对应的后向误差为:

δ(n)=d(n)-XT(n)W(n)

(8)

并且根据文献[14]的推导可知,δ(n)和δ(n-1)等都与输入噪声无关。

目前已针对RLS算法进行改进,主要是针对式(2)遗忘因子和式(4)矩阵迭代过程2个部分。

(1) 针对遗忘因子的改进,主要是将遗忘因子改为关于后向误差的函数,如文献[15]将遗忘因子改为:

(9)

类似地,文献[16]将遗忘因子改为:

λ(n)=λmin+1-λmin2L(n)

(10)

L(n)=-round(μe2(n))

(11)

(2) 针对自相关矩阵计算的改进则是为了保证式(3)的卡尔曼增益向量保持非0,在式(4)添加了自干扰项。如文献[17]中的改进项为:

PMM(n-1)+round(γe(n))]

(12)

但在实际仿真测试后发现,以上的改进都有算法复杂度增加或鲁棒性减弱的缺点。

此外,针对式(3)的改进,已有的研究较少且未进行充分讨论,故不作说明。

2 算法改进

在自适应自干扰对消问题中,多种复杂的信号有可能超出经典RLS算法的输入范围,且在应对接收信号突变时,经典RLS算法和已有的改进算法在迭代时,滤波器系数均易产生较大的当次误差,引起滤波器系数的变化。

本文提出一种均衡型-递归最小二乘法(KB-RLS)算法,以期在保证抵消效果的同时,满足各个变化方向的要求。其中,算法主要改进的点在于:

(1) 将遗忘因子设置为:

(13)

式中:a,b,c,m为常量,c作为初始因子,保证了收敛因子的最小取值;同时误差e(n)和前次误差e(n-1)的引入保证了在不增加运算量的同时,减少了突变信号对滤波器系数的过分影响,同时需保证λ(n)≤1。

(2) 将自干扰项的增加为:

ρ(n)=αIround(γ(e(n)+oe(n-1)))

(14)

式中:γ和o为2次误差的经验系数;α为该自干扰项的影响因子;I为单位矩阵;round函数则能保证避免精度过高导致的数值溢出。

在PMM矩阵计算过程中加入自干扰项,同样引入了当次误差e(n)和前次误差e(n-1),同时考虑到算法复杂度的问题,选择了二元一次项的形式进行设计。

最终改进的KB-RLS算法流程为:

X(n)=[x(n),x(n-1),…,x(n-M-1)]T

W(n)=[w0(n),w0(n),…,wM-1(n)]

ifλ(n)>1,则λ(n)=1

e(n)=d(n)-WTX(n)

W(n)=W(n-1)+K(n)e(n)

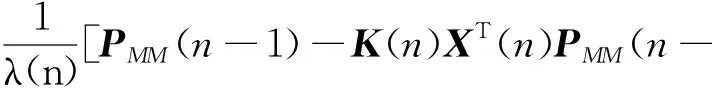
1)+αIround(γ(e(n)+oe(n-1)))]

式中:a,b,m均为调节系数,需实测;在计算迭代矩阵PMM时,γ和o分别为计算自干扰项时2次误差的经验系数;α为该自干扰项的影响因子;I为单位矩阵;X(n)为输入信号序列;d(n)为参考信号序列;e(n)为当次误差;k(n)为增益向量;W(n)为权植向量;PW为迭代矩阵。

考虑到算法改进可能带来的运算量增加,将该算法与文献[17]提到的指数窗截取(EW)-RLS、经典RLS算法进行运算量对比。算法运算资源统计见表1。

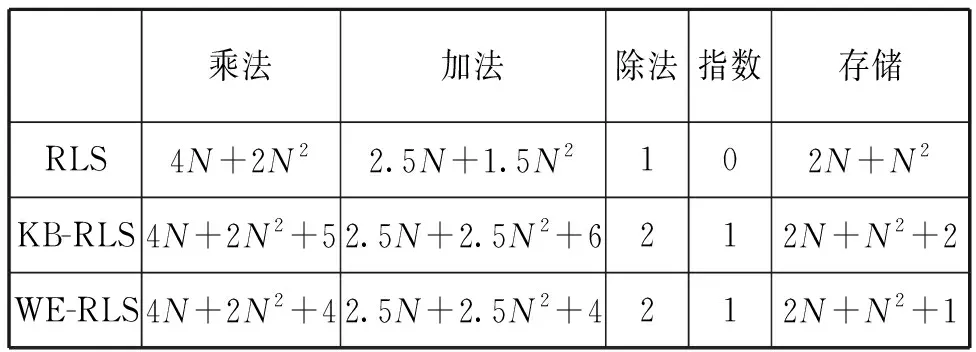
表1 算法运算资源统计表

表1表明,在运算资源方面,改进的KB-RLS算法与另外2种RLS算法保持在同一量级,未过分增加运算资源的消耗。

3 算法仿真

为了验证该算法的可靠性,本文进行了简单的算法仿真验证,并与经典RLS算法和文献[17]改进的EW-RLS算法进行对比,仿真信号参数见表2。

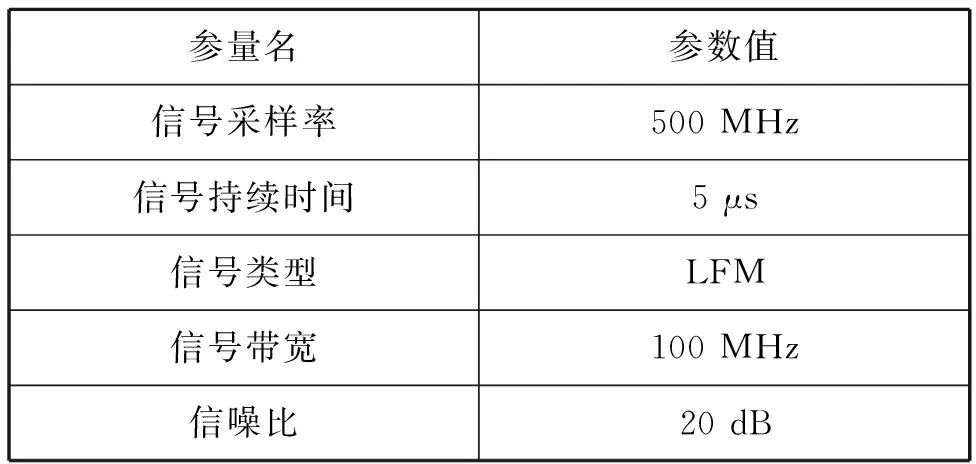
表2 LFM信号测试参数表

该测试信号的时域图谱和频域图谱如图2所示。

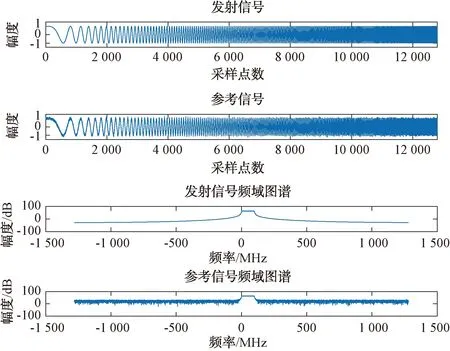
图2 测试信号时域频域图谱

分别利用经典RLS算法、EW-RLS算法和本文提出的算法对该信号进行对消处理,处理过程中3种算法的学习曲线如图3所示。

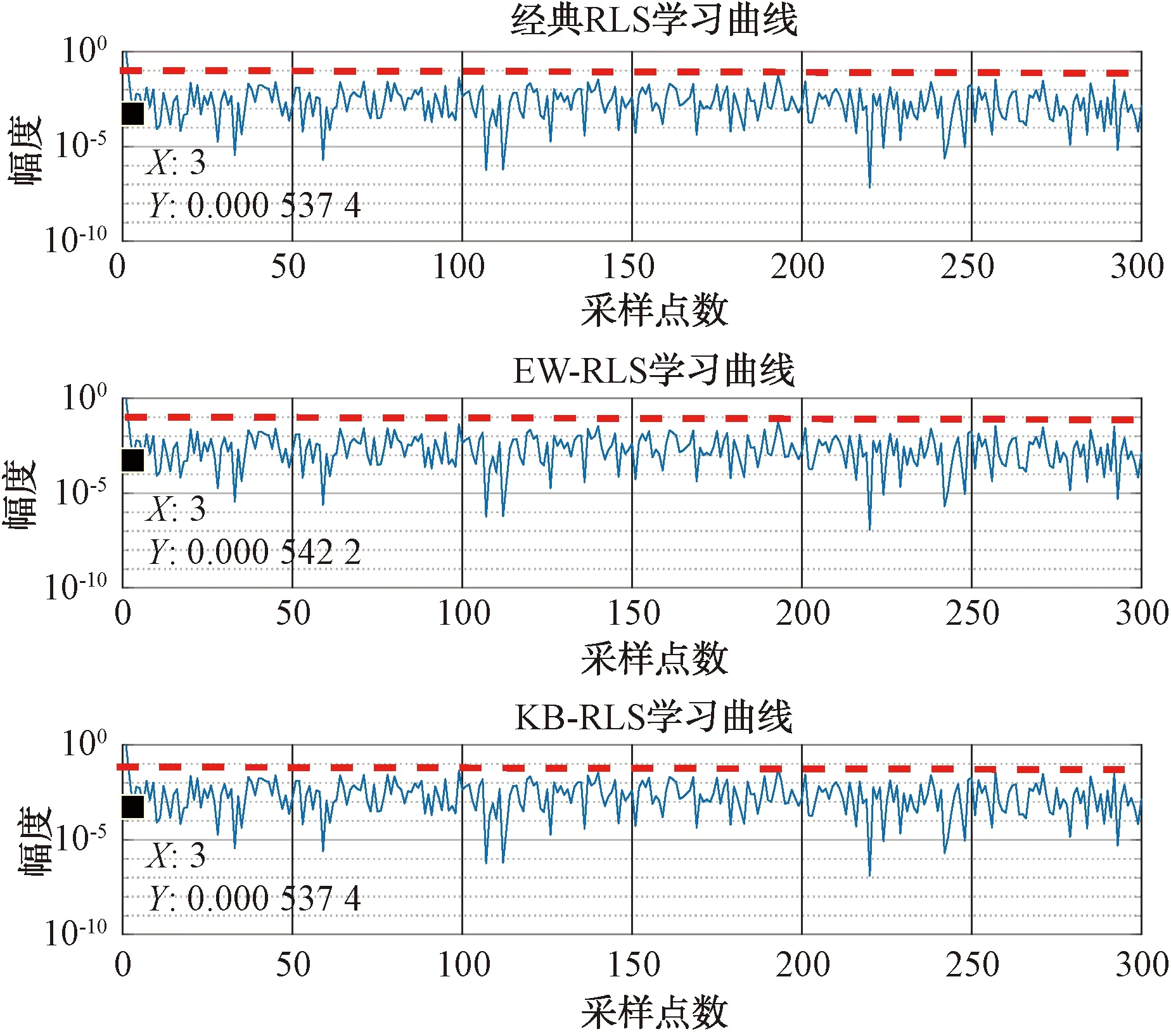
图3 3种算法迭代过程学习曲线

由图3可见,3种算法在迭代3次后,误差曲线均降至10-1以下,最终的对消结果见表3。

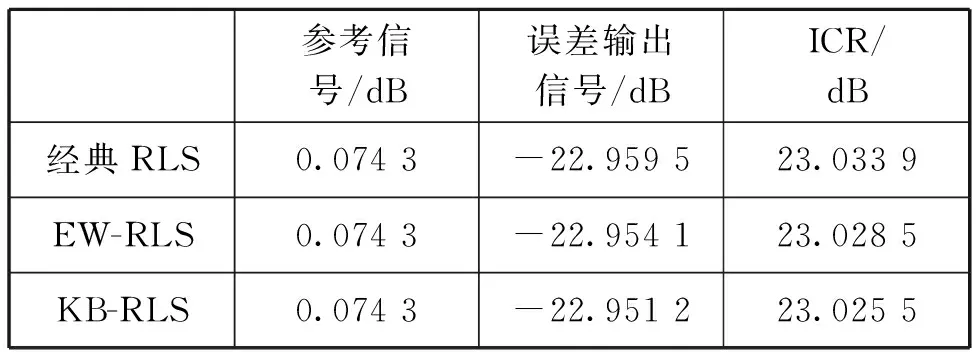
表3 LFM信号对消测试结果统计表

即3种算法对消比为23.033 9 dB、23.028 5 dB、23.025 5 dB,基本保持一致。

对该信号进行多次测试后,绘制测试结果曲线如图4所示。

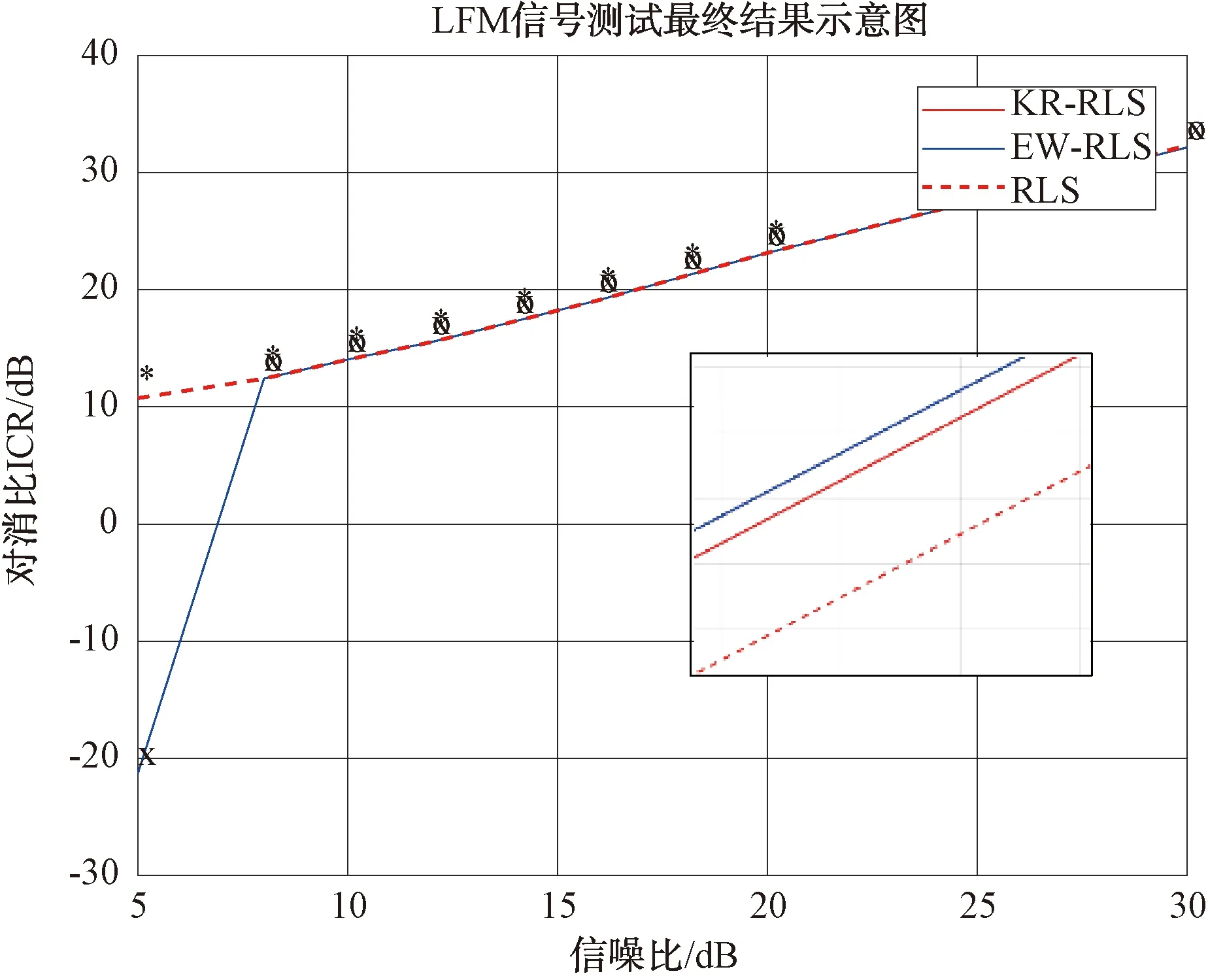
图4 单脉冲LFM信号测试对消结果图

在该项测试中,KB-RLS算法和经典RLS算法均能保持较好的对消精度,但EW-RLS算法在低信噪比时对消效果较差;此外,在该测试中,KB-RLS算法的对消精度始终高于经典RLS算法。

将该测试信号进行脉冲调制,参数见表4。

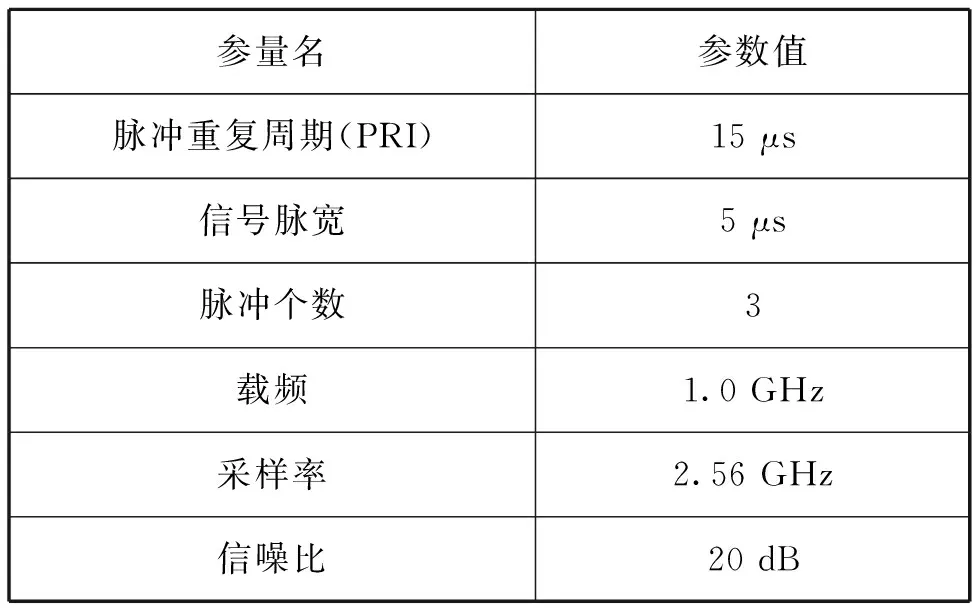
表4 脉冲调制信号测试参数表

再次利用RLS和KB-RLS 2种算法对该测试信号进行对消处理,对消过程中的误差信号图谱如图5所示。

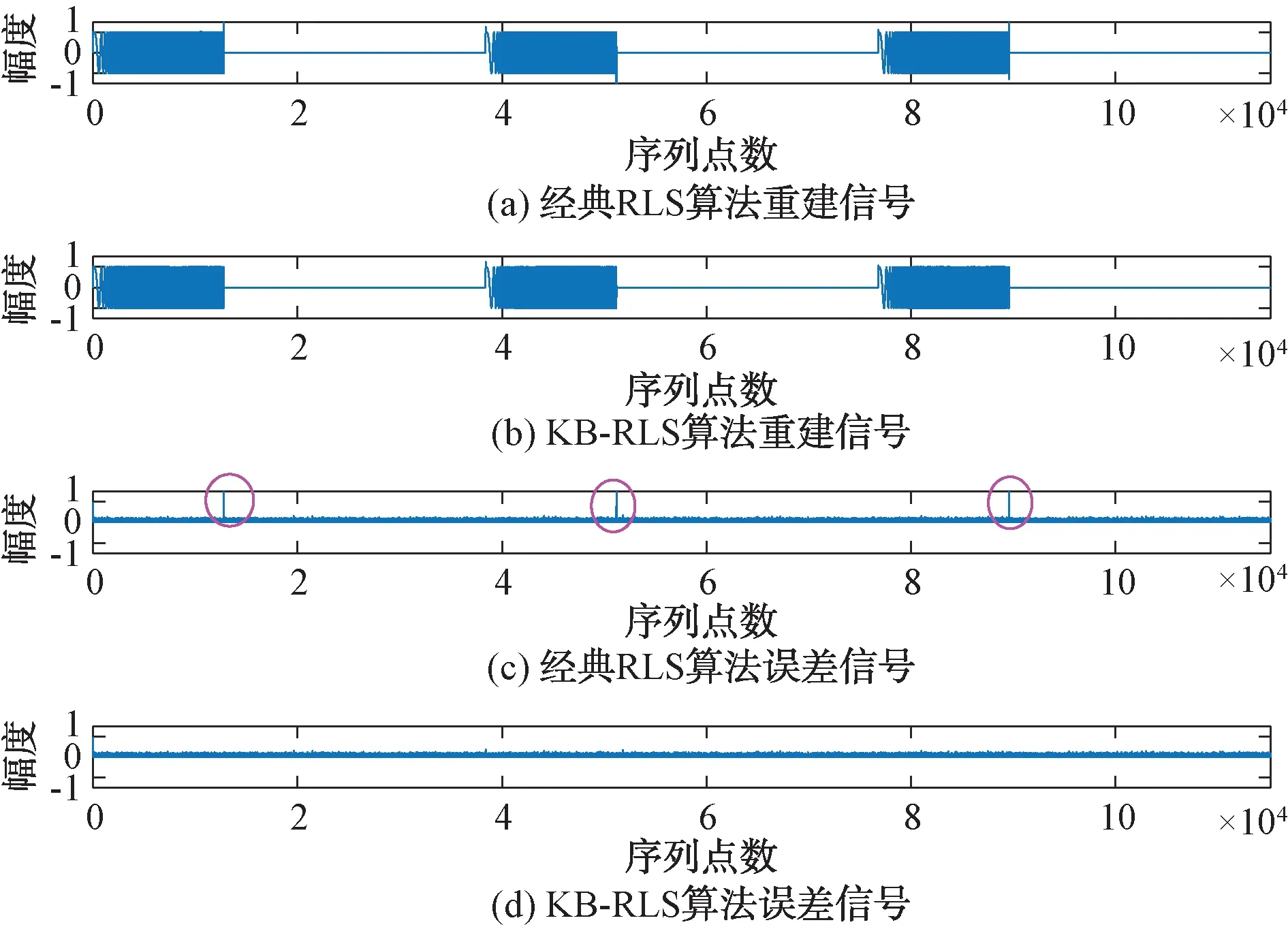
图5 脉冲信号对消重建、参考信号时频域图谱

最终的对消结果则见表5。

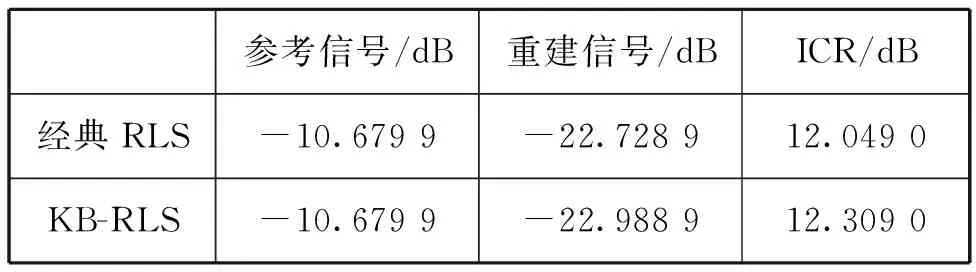
表5 脉冲信号对消测试结果统计表

在该次测试下,KB-RLS的对消精度高于RLS算法的对消精度,且在脉冲信号变化时,KB-RLS算法更好地克服了改变带来的误差。

同样地,绘制多脉冲测试下的对消结果,如图6所示。

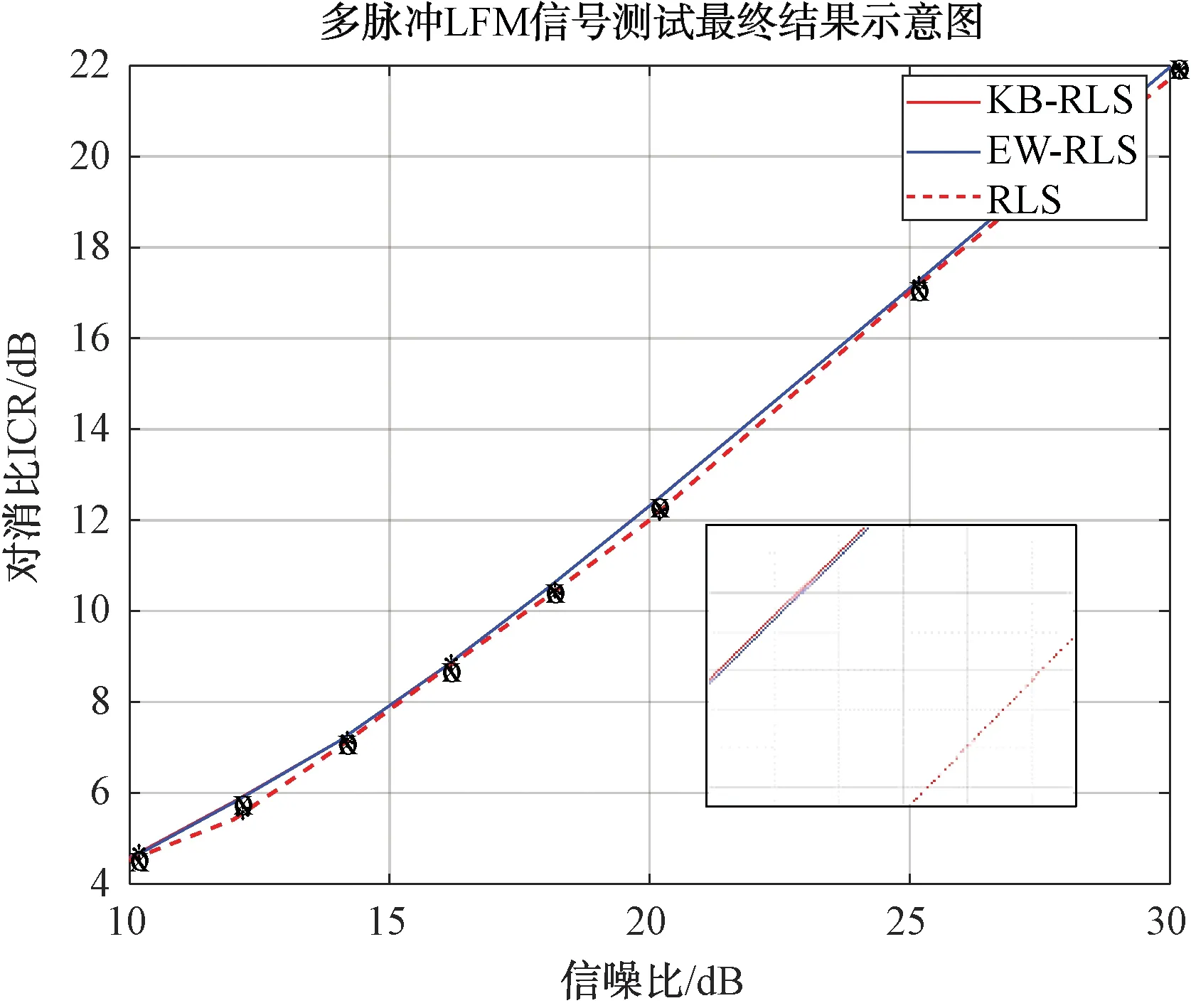
图6 多脉冲LFM信号对消测试结果示意图

另外,绘制信噪比为10 dB、15 dB、20 dB、25 dB环境下2种算法的误差曲线,如图7所示。

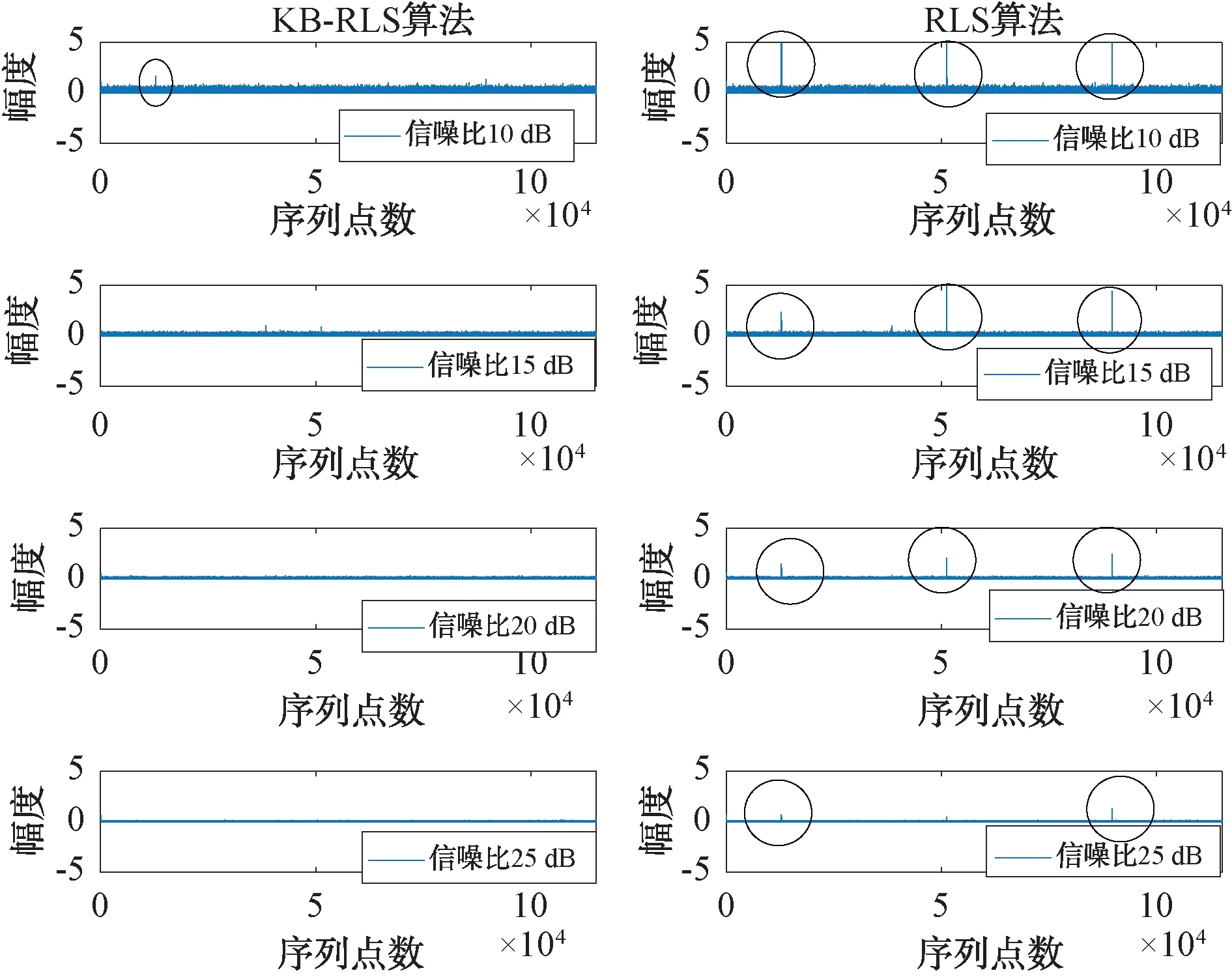
图7 多脉冲LFM信号仿真误差曲线

对本文的实验结果进行分析后,得到结论:在本次仿真测试中,KB-RLS算法在保持不输RLS算法收敛、对消精度的前提下,面对脉冲信号可以更好地克服信号突变带来的影响。

4 结束语

本文基于已有RLS算法的研究,结合自适应自干扰对消的实际工程需求,在保证一定收敛精度并保持较快的收敛速度,以及保证算法的低复杂度的前提下,对遗忘因子和自干扰项进行优化,提出了一种改进型KB-RLS算法。通过仿真,该算法在进行自适应干扰对消时,不但能获得高于经典RLS算法的对消结果,更能有效避免输入信号突变所引起的误差增大问题。