基于岭回归和GM1,1组合的上海市物流需求预测模型

吴乐 陈刚

摘  要：为了提高上海市物流需求量预测精度，运用GM1，1和岭回归组合预测方法基于9个影响因素构建需求预测指标体系，选取近13年的历史数据预测上海市未来4年的物流需求量并与BP神经网络和GM1，1预测模型进行对比。结果表明，文章提出的组合预测模型预测精度优于其他模型，其均方根误差和平均相对误差分别至少减少了42.8%和45.4%，证明模型的优越性和可行性，可为其他地区的物流需求预测提供研究方向。

关键词：岭回归模型;GM1，1模型;物流需求预测;上海市

中图分类号：F259.27    文献标志码：A    DOI：10.13714/j.cnki.1002-3100.2023.15.002

Abstract： In order to improve the prediction accuracy of Shanghai's logistics demand， the GM1，1 and ridge regression combined forecasting method is used to construct the demand forecasting index system based on nine influencing factors. The historical data of the past 13 years are selected to predict the logistics demand of Shanghai in the next 4 years and compared with the BP neural network and GM1，1 prediction model. The results show that the prediction accuracy of the combined forecasting model proposed in this paper is better than other models， and its root mean square error and average relative error are reduced by at least 42.8% and 45.4% respectively， which proves the superiority and feasibility of the model and can provide research directions for logistics demand forecasting in other regions.

Key words： ridge regression model; GM1，1 model; logistics demand forecasting; Shanghai

0  引  言

近年来，随着全球经济和物流行业的快速发展，上海市作为中国国家中心城市、沪杭甬大湾区核心城市，地处长江入海口，其每年物流货运量巨大。因此，预测上海市未来物流需求量具有重要的现实意义，有助于了解社会经济活动对物流供给能力的需求强度，从而保障供给平衡，为高效社会物流活动的实现提供基础[1]。

针对物流需求预测问题。首先，多数学者使用不同模型进行仿真预测[2-3]，其预测方法主要包括BP神经网络[1]、灰色预测模型[4]、随机森林[5]、时间序列[6]等。还有部分学者将组合预测方法进行实际应用，如黄建华[7]提出了改进GM-BPNN组合预测方法，利用ARIMA和遗传算法分别改进GM1，1和BPNN，更具有效度确定加权系数并构建线性组合模型进行预测。其次，多数学者在分析物流需求量影响因素及其指标体系的构建过程时一般会选择常用的指标[1]，但未能得到良好的预测结果[3]。人口规模在影响全球经济发展和人民日常生活[8]的同时也会明显影响物流需求量的变化，因此将其作为影响因素之一。

基于此，本文结合以往学者研究物流需求预测影响因素基础上使用9个影响因素基于GM1，1和岭回归组合预测模型预测上海市未来4年物流需求量。

1  模型介绍

本文在进行上海市物流需求预测时首先使用GM1，1模型进行影响因素预测，再使用岭回归模型对物流需求进行预测，此操作适用于研究不确定性系统。

1.1  GM1，1模型

灰色系统理论预测模型中学者们最常使用的就是GM1，1模型，1，1表示对一个一阶方程的自变量进行预测，其一般计算步骤如下：

Step 1：获得初始序列X=X1，X2，…，XN。

Step 2：将各时刻数据依次累加得到累加序列X=X1，X2，…，XN。

Step 3：判断序列X的级比σk===ρk+1，此时，随着k增加，ρk会逐渐接近0，当ρk∈0，0.5时X有准指数规律时，便可进行灰色系统建模预测。

1.2  岭回归模型

当回归方程自变量之间出现多重共线性问题时，使用最小二乘法进行预测的估计量均方误差会变得很大，因此，于1962年Heer对最小二乘方法进行改进提出岭回归[9]，其表达式为：

w=

XX+λIXy                                            （1）

其中：λ為岭系数，I为单位矩阵。岭回归属于一种有偏估计，通过引入惩罚项来减少不重要因素的重要度得到更好的估计，其代价函数为：

Jθ=

hx-y

+

λ

θ                                    （2）

通过公式可以得到岭回归方程，再输入影响因素预测值即可上海市物流需求预测。

2  上海市物流需求预测

2.1  上海市物流需求预测模型构建

在物流需求预测时，不合适的指标会导致预测效果变差且增加数据收集的工作量，因此需要结合本地发展特性选取合适的影响因素以建立合适指标体系预测。对不确定变化数据预测时，仅用外推方法进行预测会导致预测偏差大，而通过外部因素结合时间发展进行预测更能获得准确的结果。本文给出预测模型图如图1所示。

首先，本文考虑多重共线性问题，选择总均方误差最优的岭回归预测方法。其次，在进行物流需求预测时岭回归需要输入影响因素的未来预测值，此数据通过GM1，1模型进行预测即可。最后，输入历史数据到岭回归模型中即可获得岭回归方程，将获得的影响因素预测数据输入岭回归方程中预测未来4年的物流需求数据。此组合预测模型通过GM1，1预测影响因素与岭回归预测物流需求的方法相结合从而实现结果的准确性。

2.2  物流需求指标体系建立

如图1所示，在获得物流需求预测结果之前需要构建指标体系，指标体系的构建关乎预测结果的准确性。因此，一般选择与输出指标相关性强的影响因素，参考文献[1]可知经济指标、消费水平、对内和对外贸易是常用影响因素。然而随着新冠疫情的到来，物流行业在一段时间内发展缓慢、国外疫情严重无变好趋势、外部输入导致国内疫情反复都要求考虑国际形势和国内突发事件的影响，张森[10]认为在一个地区内消费水平由人口密度决定，人口密度越大消费水平越高，物流需求量越大，同时人口密度一般由常住人口数进行计算。基于此，本文在做上海市物流需求预测时增加常住人口数指标建立新的指标体系，并以货运量为输出向量，考虑数据可得性选取2009—2021年的上海市各类数据作为原始数据，如表1所示。

3  实例分析

为检验本文模型方法的可行性和有效性，第一，本文基于历史数据得到预测值验证其可行;第二，对比预测模型与BP神经网络、GM1，1的预测结果，并通过均方根误差、平均相对误差和拟合优度三个方面预测结果来评价本文改进模型的优越性。

3.1  数据获取与处理

通过上海市统计局官网查询得表1中的相关指标数据，基于数据可获得性，整理了2009年至2021年的上海市物流需求预测相关数据，如表2所示。

3.2  实例验证

根据图1流程，首先进行岭回归预测，第一步：确定K值，如图2所示。

图2以可视形式化展示了本次模型的各个自变量的标准化系数趋于稳定时的情况，并根据方差扩大因子法确定K=0.153，为了更好地展示效果，将原先横坐标幅度由0～1至0～0.10。

第二步：输出岭回归分析结果如下，基于F檢验显著性P值为0.120*，水平上不呈现显著性，接受原假设，表明自变量与因变量之间不存在着回归关系。同时，模型的拟合优度R为0.932，模型表现较为优秀。模型的公式：Y=126 228.768+0.517×X

+258.335×X+5.32×X+0.522×X+0.061×X-67.991×X-0.149×X

+1.597×X+3.712×X，最终结果如表3所示。

第三步：对二级指标X—X使用GM1，1模型预测未来4年的数值，得到结果如表4所示。实验发现总体预测趋势良好，其影响因素的预测偏差仅为0.5～4%。最重要的是，所有影响因素平移转换后序列的所有级比值都位于区间0.867，1.154内，说明平移转换后序列适合构建灰色预测模型。

第四步：将影响因素的预测数据输入岭回归方程中即得到未来4年上海市物流需求量预测值，如表5所示。

3.3  不同模型预测效果对比分析

为了验证本文模型和方法的优越性，现从横向和纵向分析其优越性并以平均相对误差、均方根误差和拟合优度进行评比，其中MAPE和RMSE公式如下：

MAPE=                                        （3）

RMSE=                                      （4）

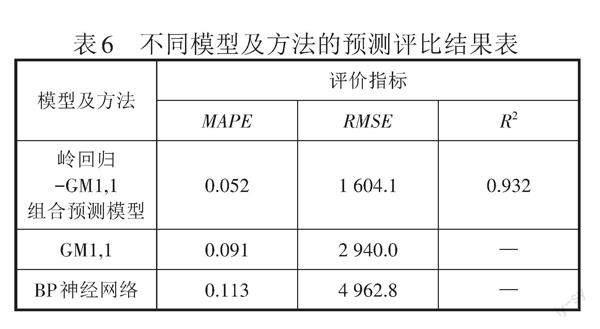
基于此，给出表6不同模型的MAPE、RMSE和R值，可以发现本文模型在三个方面都优于其他模型和方法，并至少减少了25.3%的平均相对误差、30.34%的均方根误差及更优的拟合优度，证明本文所选模型和方法的可行性和有效性。

此外，为了直观观察给出图3不同模型对上海市物流需求预测结果对比图，可以发现红色线条的预测效果最好。

4  结  论

本文利用上海市物流需求预测相关影响因素建立了岭回归-GM1，1组合预测模型。基于以往学者在进行物流需求预测影响因素指标体系基础上分析了海市物流需求的9个主要影响因素，重新构建需求指标体系进行预测。同时鉴于上海市物流需求在总体上表现为波动大、难预测特点上，使用岭回归和GM1，1组合预测，在过程中先对影响因素使用GM1，1得到的预测结果，结合新指标体系在岭回归结果上进行未来4年的上海市物流需求预测。最后，在研究中对比了本文提出的模型、GM1，1和BP神经网络的平均相对误差、均方根误差和拟合优度指标，来证明本文模型方法的可行性和优越性。

最终结果表明，本文预测未来4年上海市物流需求逐年上升，岭回归-GM1，1组合预测模型能更好地预测上海市物流需求，同时能有效减少不确定数据预测问题，可为其他市区的物流需求预测提供方向。

参考文献：

[1] 杨麒，张志清. 基于BP神经网络法和二次指数平滑法的珠海市物流需求预测比较分析[J]. 物流科技，2022，45（15）：27-32.

[2] 武亚鹏，李慧颖，李婷，等. 基于多模型组合的物流需求预测分析——以武汉市为例[J]. 物流技术，2022，41（6）：60-63.

[3] 邓熠. 基于BP神经网络的福州都市圈物流需求预测[J]. 物流工程与管理，2022，44（8）：29-31.

[4] 刘新文，刘晓霞. 广西R&D投入强度预测——基于灰色GM1，1模型[J]. 生产力研究，2022（9）：55-60.

[5] 夏伟怀，刘嘉莉，冯芬玲. 基于随机森林的铁路冷藏运输需求预测[J]. 铁道科学与工程学报，2022，19（4）：909-916.

[6] 徐子涵. 基于组合模型的合肥市航空货运需求预测研究[D]. 合肥：安徽理工大学，2020.

[7] 黄建华，张迪. 面向不确定物流需求的改进GM-BPNN组合预测方法[J]. 统计与决策，2022，38（16）：26-29.

[8] 段容谷，庄媛媛，张克勇，等. 突发公共卫生事件下多阶段应急救援物资配置研究[J]. 中国安全生产科学技术，2021，17（12）：142-148.

[9] 邵楠，许冰. 基于岭回归的大坝变形位移模型[J]. 测繪与空间地理信息，2021，44（6）：191-192，196.

[10] 张森. 基于粗糙集理论和最小二乘支持向量机的区域物流需求预测研究[D]. 深圳：深圳大学，2020.

[11] 刘玉囡，闫国东，纪如雪. 港口物流与旅游经济的协调发展研究——基于面板数据的实证分析[J]. 物流科技，2022，45（7）：17-21，32.

收稿日期：2023-05-23

基金项目：国家自然科学基金资助项目（71761006）

作者简介：吴  乐（1997—），男，安徽滁州人，贵州大学管理学院硕士研究生，研究方向：物流与供应链管理;陈  刚（1987—），男，四川广安人，贵州大学管理学院，副教授，博士，研究方向：物流系统优化。

引文格式：吴乐，陈刚. 基于岭回归和GM1，1组合的上海市物流需求预测模型[J]. 物流科技，2023，46（15）：6-9.