基于CFD方法对串列翼飞行器动导数的计算
杨起帆 郭家宁 周兵 王际洲


摘 要:本文基于计算流体力学方法,通过强迫俯仰振动法及差分法对串列翼布局的小型低速飞行器进行了动导数的计算研究,又使用该方法对某串列翼布局的小型无人飞行器进行了纵向动导数的计算,验证了CFD方法计算复杂外形飞行器动导数的可行性。本文选取了一例动导数标准模型Basic Finner的算例进行计算,并与文献数据进行了比较,计算结果表明,CFD方法估算动导数具有较高的可靠性与工程精度,进一步验证了该方法的准确性与可靠性。串列翼布局的飞行器纵向动导数计算结果表明,CFD方法可以较好地对串列翼布局飞行器或其他非常规布局的飞行器进行动导数估算,为工程应用提供了可选解决方案。
关键词:动导数;CFD;串列翼;非常规布局
文献标识码:A
飞行器动导数是指飞行器所受的气动力与气动力矩对飞行器运动参数的导数,如俯仰力矩系数随俯仰角变化的动导数。飞行器动导数是求解小扰动方程特征根不可或缺的基本参数,而飞行器不同模态的阻尼比、自然频率、周期以及倍幅时间都是由该模态的特征根决定的,因此飞行器的动导数直接决定了飞行器的飞行品质及响应。过去获取动导数的方法包括飞行试验、风洞试验或工程估算。对于小型低速无人机而言,飞行试验与风洞试验周期太长,成本过高。而工程估算方法以一些经验或半经验公式为主导对飞行器的动导数进行估算,但是这些经验或者半经验公式都是基于常规布局发展而来,因此对于非常规布局的飞行器进行估算时会有较大的误差,甚至产生错误的结果[1]。对于串列翼布局的飞行器而言,初步设计软件如XFLR5就难以给出满足需求的结果。
计算流体力学(CFD,Computational Fluid Dynamics)作为一门流体力学与数学的交叉学科,是通过数值方法来求解流体力学的控制方程。随着近现代计算机的高速发展,使用计算流体力学作为手段来估算飞行器气动特性已得到广泛应用。CFD手段与传统风洞试验相比有成本低、速度快等优点,在设计阶段可以快速迭代优化或者进行气动外形的再设计。
来自NASA兰利研究中心的Lawrence L.Green等人[2]最早提出可以使用CFD手段计算飞行器的动导数。叶川、马东立[3]使用强迫俯仰振动法与差分法对Finner导弹标准模型进行了计算,验证了该方法的准确性。米百刚、詹浩与朱军[4]在强迫俯仰振动法与差分法之外,进一步研究了准定常方法求解动导数。而孙涛、高正红、黄江涛[5]研究了在使用强迫俯仰振动法与差分法求解动导数过程中减缩频率对计算结果的影响。本文使用精度较高的强迫俯仰振动法与差分法对某串列翼布局的小型低速倾转旋翼无人机进行了动导数计算。
1 控制方程与数值方法
1.1 控制方程
计算流体力学中对流动的控制方程为NS方程[6]。三维NS方程的守恒形式如下:
Ut+Fx+Gy+Hz=J(1)
其中:
U=ρ
ρu
ρv
ρw
ρ(e+V22)
F=ρu
ρu2+p-τxx
ρvu-τxy
ρvu-τxz
ρe+V22u+pu-kTx-uτxx-vτxy-wτxz
G=ρv
ρuv-τyx
ρv2+p-τyy
ρwv-τyz
ρe+V22v+pv-kTy-uτyx-vτyy-wτyz
H=ρw
ρuw-τzx
ρvw-τzy
ρw2+p-τzz
ρe+V22w+pw-kTz-uτzx-vτzy-wτzz
J=0
ρfx
ρfy
ρfz
ρufx+vfy+wfz+ρq·
其中列矢量U为流动的原始变量项,列矢量FGH为通量项,列矢量J代表源项。
1.2 数值方法
考虑到需要求解的飞行器设计巡航速度为0.1马赫,因此求解过程中可以将流动近似为不可压缩流动。空间离散采用有限体积法,数值计算采用针对不可压流动的SIMPLE算法,其中动量方程与压力方程都使用二阶迎风格式。时间离散采用二阶向后欧拉格式。湍流模型使用kωSST(剪切应力输运)双方程模型。
而對于动导数标准模型finner导弹,由于其超声速的特性,使用针对可压缩流动的Roe通量分裂格式,空间上使用二阶迎风格式。
2 动导数的计算方法
对动导数的求解主要使用强迫俯仰振动法与差分法相结合。
2.1 强迫俯仰振动法
基于小扰动简化假设与气动力线化解耦[1],受扰动后的气动力与力矩形式为(略去高阶项):
ΔCm=Cmuu+CmαΔα+CmθΔθ+Cmα·Δα·+
Cmqq+CmδeΔδe+CmδtΔδt+…(2)
对于受扰动的飞行状态,式中u为无量纲化的来流速度变化量,俯仰角速度q为俯仰角变化量
u=ΔUU0 q=Δq
对于巡航状态下的飞行器,来流速度u,当地水平面与飞机参考轴之间的夹角θ,升降舵偏转角δe与发动机操纵参数δt的变化量均为0。同时对于以ω为频率作小幅俯仰运动的飞行器而言,其俯仰角速度等同于其迎角变化率。因此将式(2)简化为如下形式:
ΔCm=CmαΔα+Cmα·Δα·+CmqΔα·(3)
对于强迫俯仰运动,飞行器做周期性小幅俯仰运动,因此定义迎角变化如下:
Δα=αampsin(ωt) Δα·=kαampcos(ωt)
其中αamp为振幅,k为减缩频率:
k=ωlref2VSymboleB@
俯仰力矩系数随时间变化的公式如下:
Cm=Cm0+ΔCm(4)
其中Cm0为无扰动情况下的俯仰力矩系数,ΔCm即为式(3):
Cm=Cm0+Cmααampsin(ωt)+(Cmα·+Cmq)kαampcos(ωt)(5)
通过CFD方法可以求得俯仰力矩系数(Cm)随时间变化的曲线,忽略其中受到初始条件影响的部分,对周期性变化的曲线部分进行最小二乘法回归即可得到式(5)中的三个系数:无扰动下的俯仰力矩系数Cm0、俯仰力矩系数随攻角变化的静稳定性导数Cmα以及俯仰组合导数(Cmα·+Cmq)。
2.2 差分法
使飞行器进行定常圆周运动,以定常拉升运动为例,改变飞行器的俯仰角但使其迎角保持不变。因此Δα与Δα·为0,简化式(2)并代入式(4)可得:
Cm=Cm0+Cmqq-(6)
其中q-为无量纲化俯仰角速度:
q-=ql2V
对于圆周运动而言,线速度为角速度乘以半径,V=qR。故:
q-=ql2qR=l2R
对半径R选取不同的值进行多次CFD定常计算即可求得俯仰力矩系数对俯仰角速度的动导数Cmq。同时也可求得2.1节中俯仰组合导数中的俯仰力矩系数对迎角变化率的动导数Cmα·。
3 对某串列翼布局飞行器的计算
3.1 参数设置与网格划分
該串列翼无人机几何尺寸如图1所示。网格划分采用非结构化网格,无人机表面网格如图2所示,总网格数为190万。根据Thomas H.Pulliam[7]的研究,对算例进行网格无关性与远场无关性进行验证。对于该低速低空无人机选取来流M∞=0.1,初始攻角α0=0°,减缩频率k=0049,振幅αamp=2°,重心为俯仰平面内距离机头前缘三倍弦长处,远场距离飞行器40倍弦长处,采用滑移网格模拟飞行器的周期性振动。
3.2 俯仰组合导数求解
每时间步长设为0.01秒,最大迭代次数为50次,收敛条件限制连续性方程残差小于1×10-6。求得图3俯仰力矩系数随时间变化的曲线。
从上图可以看到俯仰力矩系数与瞬时迎角之间存在迟滞效应,这是非定常计算中出现的典型现象。图4为该串列翼布局飞行器的迟滞环。可以看到部分计算结果受到了初始条件的影响,因此对于图3中的俯仰力矩曲线截取不受初始条件影响,呈周期性变化的部分并进行前文2.1节所提及的系数回归可得下文表1中的无扰动俯仰力矩系数Cm0,俯仰静稳定导数Cmα和俯仰组合导数(Cmα·+Cmq)。
3.3 俯仰阻尼导数求解
为了求解俯仰阻尼导数,需要对作匀速圆周运动的飞行器进行计算,采用多重参考系法,计算结果如图5所示:
根据2.2节的推导,无量纲俯仰角速度q-只与旋转半径R有关。但是为了保证飞行器的飞行速度V不发生改变,因此在改变半径进行计算时也需要改变俯仰角速度q与之匹配。计算结果图6所示,通过求解图6曲线的斜率可求得俯仰力矩系数对俯仰角速率的动导数Cmq,同时也可从3.2节中所求得的俯仰组合导数中解耦求得俯仰力矩系数对迎角变化率的动导数Cmα·。
4 有翼导弹动导数计算
为验证CFD方法的可靠性,对国际动导数标准模型finner导弹选取算例进行计算,计算模型、计算参数及计算结果的对比参照Erdal Oktay[8]等人的报告。
4.1 计算参数与算例选取
Finner导弹模型及表面网格如图7所示:
选取算例中以下参数均与原文[8]参数保持一致,马赫数M∞=2.1,减缩频率k=0.00316,xcg=5d,其中d为弹体直径。网格采用非结构化网格,总网格量为203万,计算远场位于45d,计算模型采用sstkw湍流模型,隐式时间推进,振幅选取αamp=3°。计算非稳态解的方法与原文[8]保持一致,即计算0°攻角下的稳态解,再以稳态解为初始条件计算攻角随时间变化的非稳态解。非稳态的每时间步长设为0.01秒,最大迭代次数为50次,收敛条件限制连续性方程残差小于1×10-6。
4.2 俯仰组合动导数计算结果
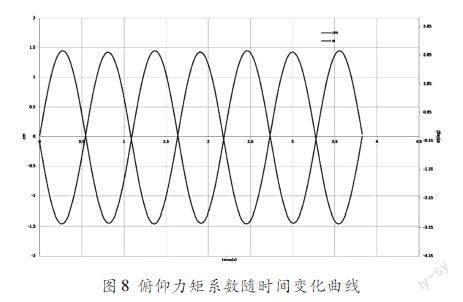
俯仰力矩系数随时间变化曲线如图8所示:
计算结果如表2所示:
从选取的算例可以看出本文选取的攻角变化速率、攻角变化幅度与原文[8]所使用的攻角变化速率、攻角变化幅度有所不同,依然能较好地预测俯仰静稳定导数与俯仰组合动导数。
结语
本文使用CFD方法对串列翼布局的小型低速无人机进行了纵向的静稳定性导数和一些动导数的计算。同时为了验证CFD计算结果的可靠性,本文对国际动导数标准模型basic finner导弹进行了计算,计算结果表明CFD计算方法对获取飞行器的动导数具有较好的可靠性和较高的工程精度。
因此,对于具有复杂气动外形或者非常规布局的飞行器,若不适合使用工程估算、半经验方法或风洞实验,则可以在飞行器基本气动外形确定后使用CFD方法计算这些导数,用于判断飞行器的飞行品质与响应,以及设计飞机的飞行控制與导航系统。
参考文献:
[1]班度·N.帕玛迪.飞机的性能、稳定性、动力学与控制[M].第2版.北京:航空工业出版社,2013.
[2]Lawrence L.Green,Angela M.Spence,Patrick C.Murphy.Computational Methods for Dynamic Stability and Control Derivatives[R].AIAA,20040015 January 2004.
[3]叶川,马东立.利用CFD技术计算飞行器动导数[J].北京航空航天大学学报,2013(2):196200.
[4]米百刚,詹浩,朱军.基于CFD数值仿真技术的飞行器动导数计算[J].空气动力学学报,2014(6):834839.
[5]孙涛,高正红,黄江涛.基于CFD的动导数计算及减缩频率影响分析[J].飞行力学,2011,29(4):1518.
[6]小约翰·D.安德森.计算流体力学:基础与应用[M].北京:航空工业出版社,2018.
[7]Thomas H.Pulliam.Solution methods in Computational Fluid Dynamics[R].Moffett Field:NASA Ames research center,1986.
[8]Erdal Oktay.CFD predictions of dynamic derivatives for missiles[R].AIAA,20020276,2002.
作者简介:杨起帆(1994— ),男,汉族,浙江嘉兴人,研究方向:计算流体力学。

