用于OFDR振动传感的改进型相位生成载波算法研究

刘煜　汪路军　辛玮　刘学静　张学典

关键词：光频域反射；振动传感；调制深度；相位解调算法

中图分类号：TN 253 文献标志码：A

引言

光频域反射（optical frequency domainreflectometry，OFDR） 是基于光在光纤中的背向瑞利散射的分布式光纤传感技术，可以准确定位应变所在，衍生出多种重要的应用，包括电磁场监测、结构健康监测、温度变化检测，形状传感等。特别是在振动测量领域，由于其抗干扰性好、抗腐蚀性强、易安装、成本低等优点吸引了众多的关注[1-3]。而振动信号的解调是振动传感的关键。

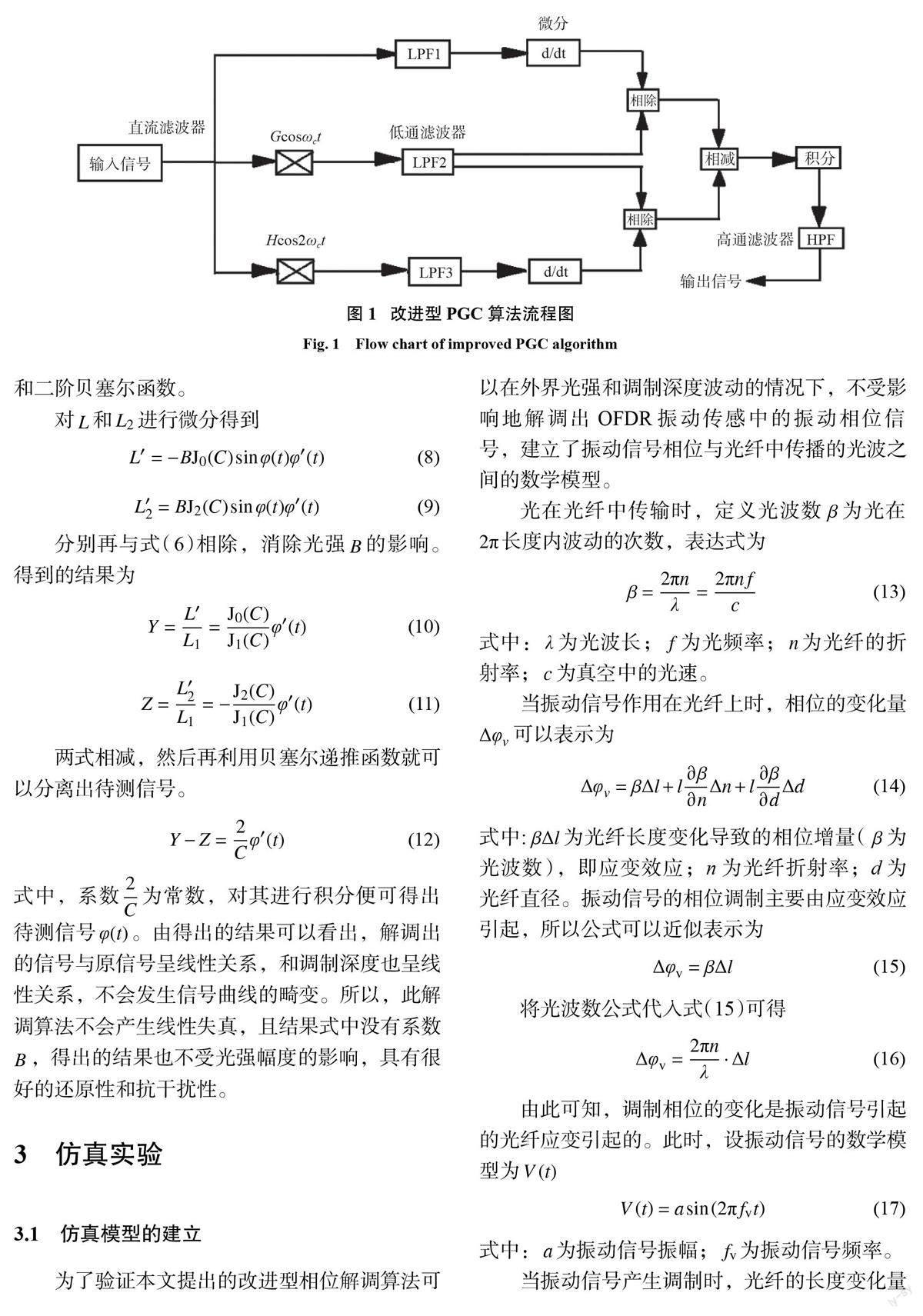
在OFDR 的探测采样过程中，需要对返回的信号进行处理，这一处理过程对频率要求比较高。根据奈奎斯特定律可知，如果要還原完整的信号，采样重复频率至少是待测频率的2 倍以上，在实际应用中，则至少要4 倍以上。假设振动信号为100 Hz，采样频率则至少为400 Hz。而扫频激光器在一次扫频后的空闲时间约为1 s，重复采样频率为1 Hz，远远达不到400 Hz 的要求。所以传统的OFDR 解调方式并不能很好地解调出振动信号。此时，便可以用分辨率高，动态范围广，线性度好，实时解调能力强的相位生成载波（phase generation carry， PGC）算法来进行解调[4-5]。

关于相位解调算法的研究有很多，Wang等[6] 用3×3 耦合器解调相位信号，方法是在构成的干涉仪中， 让相邻的两个干涉臂具有120°的相位差，利用该特点直接对光电探测器接收到的3 路信号进行交叉微分相乘，解调出信号。王旭等[7]用数字正交解调算法将瑞利散射光信号经过数学算法之后，形成两路正交信号，再将这两路信号交由解调模块进行相位的解调。

Wang 等[8] 提出一种基于时间门控数字OFDR 相位提取的分布式光纤振动传感方法，通过采用时间门控OFDR 技术实现了高空间分辨率的振动应力传感。现阶段，一般使用对调制深度敏感度不高的微分交叉解调算法来解调振动信号[9]，但是这种算法对光线内光强要求很高，易受外界影响。当要求较高时，人们会使用微分交叉和反正切相结合的算法来解调振动信号[10]，但是过程相对繁琐。本文提出了一种可以避免光强和调制深度影响的改进型算法，将其用于OFDR 振动信号的解调，并通过仿真实验验证其提高系统抗干扰的能力。

1 PGC算法

1.1 PGC调制

在实际测量中，如果对待测信号相位直接进行测量，环境噪声产生的随机相位漂移和解调电路产生的直流漂移会对解调结果产生严重的影响。可以通过引入一个待测信号带宽以外的大振幅周期信号对待测信号进行调制，使得待测信号位于调制信号的边带上，将外界的噪声影响转移到调制信号上，这便是PGC 调制[11]。经过调制可将噪声信号与待测信号分离，后续通过滤波器对信号进行简单的滤波处理，便可得到滤除了噪声信号的调制信号。

根据生成调制载波信号方式的不同，PGC调制又分为内调制和外调制。由于内调制需要改变光源的驱动电流，从而影响扫频激光器的工作，在OFDR 系统中不予采纳。本文主要介绍外部调制。

外部调制方式为在光路外部直接对参考光路光纤施加外力，使其产生周期性的调制载波信号。具体方法是将光纤缠绕在压电陶瓷换能器（piezoelectric ceramic transducer， PZT）上，通过计算机控制PZT，使其产生一个周期性的电压，从而导致PZT 发生伸缩效应，导致光纤发生形变，光纤中的光波相位发生变化，由此来实现外部调制。

1.2 PGC 传统解调方法

最常用的两种传统解调方式为微分交叉相乘解调法和反正切解调法。

1.2.1 微分交叉相乘（ differential and crossmultiplying， DCM）解调法

具体流程为：首先，将输入的干涉信号分别与基频和二倍频混频；然后，通过低通滤波器分别过滤掉高于基频和二倍频的部分；接着，将两路信号进行微分自相乘运算，得到两个正交信号的平方项，利用三角函数公式化简后对其进行积分；通过高通滤波器滤除噪声信号，最终得到解调信号[12]。解调信号表达式为

在基于OFDR 的振动传感中，式（20）模拟光电传感器采集到的信号。同时在仿真中不同的光强 值和调制深度 值模拟将影响调制结果的外界因素。

3.2 改进型PGC 算法与DCM 算法的比较

改变参数光强幅值B，模拟不同光强环境，比较两种算法对同一信号的解调结果。当使用交叉相乘算法解调时，为使调制出的信号幅值最大，由式（1）可知，当BJ₁（C） * J₂（C）值最大时，信号幅度最大最直观。计算可得，当 =2.37 时，由式（1）求得的值最大，所以在交叉相乘算法中调制深度 取值定为2.37。改变光强的值，分别取1，2，3 和4；结果如图2（a）—（d）所示。

由仿真结果可知，当光强 B 不断变化时，传统DCM 算法的波形没有发生畸变，频率也与原始信号一致，但是其幅值变化较大，需进行后续的处理。而改进型解调算法由于计算过程消除了系数 ，所以在波形、频率和幅值上与原始信号相比，几乎没有变化。仿真实验论证了光强 的改变不会对改进型算法的解调结果产生影响，方便了对信号的后续处理，能提高系统的处理速度和实时性。

3.3 改进型算法对比反正切算法

固定光强B，改变调制深度C，以此模拟相同光强环境，不同调制深度，比较两种算法对同一信号的解调结果。结果如图3（a）—（d）所示：

当调制强度C发生变化时，由于解调信号的系数含有非线性项J₁（C）=J₂（C），传统的反正切算法的解调结果相比于原始信号会有不同程度的畸变，不利于后期的处理。而改进型解调算法由于没有非线性项，解调结果的曲线不会发生畸变，但由于结果含有关于C的线性项，幅值会随着C的变化发生改变，通过简单的后续处理便可。

仿真实验结果的对比，证实了两种传统的算法各有其独自的优点和缺点。微分交叉相乘法解调出的信号相对于原始信号，其曲线没有畸变且完整，但是幅值受调制深度 和光强 的双重影响。如果后续加入对初步解调信号的再处理算法，整个处理过程会比较复杂，造成的结果就是解调缺乏实时性且容错度低。反正切算法流程简单且消除了光强 产生的影响，但由于该算法中有非线性项J₁（C）=J₂（C），只有调制深度在指定数值时，还原出的信号才是比较好的，所以其稳定性也不高。而改进型相位解调算法即使在调制深度和光源光强变化时，依旧能很好地解调出原始信号，可见其拥有优秀的抗干扰能力。

4 总结与展望

本文针对基于OFDR振动传感的相位解调部分易受光源光强和调制深度影响的问题，提出了可以消除光强和调制深度影响的改进型算法。分别从原理和仿真模拟中验证了该算法相较于传统解调算法，可以有效消除光强B和调制深度C对解调结果的影响，提高了该系统的稳定性。

虽然改进型相位解调算法在理论仿真上可以很好地提高系统稳定性，但是还没有实际应用于基于OFDR振动信号传感的实际测量，需要通过进一步实验来验证其相较于传统相位解调算法的优越性。