抗浮锚杆锚固界面渐进性失效演化机理

陶 瑞,乔建刚,李景文

(河北工业大学土木与交通学院,天津 300401)

现代城市地下空间资源的开发和利用已成为一种社会发展趋势,是保证城市可持续发展的重要措施。但是,由于缺乏对抗浮技术机理的深入了解,越来越多的建筑物出现抗浮技术失效的问题。这种失效可能会导致建筑物形变、开裂,甚至整体结构破坏,对经济造成不可预测的损失。近年来,随着计算机软件技术的飞速发展,数值模拟方法在不可见的地下工程、岩土工程及采矿工程中的应用越来越广泛,同时也为工程实践提供了指导[1]。目前的数值模拟方法中主要有有限元法、有限差分法和离散元法[2-5]。由于岩土体材料本质上可以看成是散体颗粒胶结或架空而成,因此不受变形量限制的离散元法更符合岩土体介质的物理本质[6-8]。

离散元数值模拟法广泛用来研究工程中破坏机理与细观累积损伤[9-12],PFC2D程序因其可以揭示细观层次的机理,受到了国内外学者的青睐。P.A.Cundall[13]首先在岩石工程领域中提出了离散元法(Discrete Element Method,DEM)。C.Shi等[14]利用元胞自动机建立了一种快速有效的岩石微观参数标定方法。W.R.Liu等[15]采用颗粒流程序建立了巷道模型,从接触力链、变形位移和微裂纹分布等方面分析了巷道的损伤过程。V.Sarfarazi等[16]采用颗粒流程序方法研究了有无锚杆的半圆形空间与相邻节理之间的相互作用,并通过巴西试验和单轴压缩试验对PFC参数进行了标定。周健等[17]建立了砂土的颗粒流模型,并对该模型进行了加卸载试验。刘文白等[18]采用PFC2D模拟了桩基础在上拔荷载作用下的颗粒分布和速度。彭国园等[19]建立了红黏土的颗粒流模型,并对其进行了三轴虚拟试验,探讨了颗粒选择、颗粒间粘结方式、弹性模量和泊松比等细观参数对试验结果的影响。胡训健等[20]采用PFC2D程序建立了花岗岩颗粒流细观非均质模型,并对三轴压缩试验进行了模拟,发现不同非均质性因子和不同围压下花岗岩模型的应力-应变曲线。

目前针对抗浮锚杆的数值模拟研究使用有限元方法很常见,但是针对非连续介质力学问题,尤其是当砂土被用作抗浮锚杆周围的岩土体时,有限元方法难以准确分析其破坏机制。基于此,笔者采用离散元方法对抗浮锚杆受力机理进行模拟研究,分析岩土体轴向应力和孔隙率的变化趋势,对轴线应力应变、孔隙率以及相邻锚杆的位移、接触力等指标进行监测,进一步分析锚杆失效的原因。

1 抗浮锚杆颗粒流模型的建立

1.1 工程概况

某商业广场项目由购物中心、写字楼、住宅、室外步行街等组成,总建筑面积62.45万m2。商业C区由三栋写字楼及购物中心组成,建筑面积为26万m2。地下两层主要为车库及设备机房等辅助用房。商业区地上5层,塔楼地上28层。商业C区地下室为地下二层,地下室底板板面相对标高为-10.90 m,其中地下二层设计净高为4.90 m。

2018年5月15日,施工单位发现商业C区地下室南侧中庭位置处填充墙多处裂缝,项目公司工程部安排总包单位进行质量缺陷维修。但5月30日发现维修后的墙体再次开裂,经详细观察发现,基础筏板存在不均匀沉降,导致变形。

在商业C区附近,增加地下水位观测点,水位位于1 107.85 m(相对商业零米为-3 m)左右,通过观测,近期水位波动每天约75 mm。上浮导致7道梁局部裂缝(见图1)。

图1 梁局部裂缝Fig.1 Local cracks in the beam

1.2 PFC颗粒流方法

PFC法是一种用于模拟刚性颗粒集合体运动及相互作用的方法[2],该方法旨在建立一个描述颗粒之间相互作用的模型,从而研究颗粒的运动规律和集合体的宏观行为。二维PFC中颗粒模型为圆盘,三维PFC中颗粒模型为球体。颗粒流模型中有“颗粒-颗粒”与“颗粒-墙”两种接触类型。PFC通过在一系列颗粒单元之间赋予不同接触模型来计算颗粒单元之间的受力、运动特征,进而在宏观层面上模拟出宏观试样的非线性本构关系。PFC中内嵌接触模型中最常用的三种模型为线性模型、线性黏结模型和平行黏结模型。

传统的有限元软件能够对形状规则、力学性能均匀的介质进行较好的仿真,但是对于离散性的岩土体介质,往往不能得到与真实情况相应的模拟结果,因此笔者选用离散元软件PFC进行分析。由于本次研究所建立的模型包含了3万多个颗粒,出于计算资源限制的考虑,为了更好地模拟出抗浮锚杆在岩土体中拉拔的真实效果,因此采用PFC2D进行仿真分析。

1.3 模型的建立

抗浮锚杆拉拔试验颗粒流模型共分为两部分:一部分为直接与抗浮锚杆相作用的试验岩土体区,另一部分为试验岩土体区的支撑区。由于组成岩土体的球颗粒单元较小,如果采用较小尺寸的球颗粒单元势必造成计算资源的浪费,因此球颗粒单元粒径应采用差异化的方法建立。试验区岩土体模型采用直径1～2 mm的随机粒径建立,试验支撑区岩土体采用直径1 cm的颗粒单元,设岩土体的密度为2 500 kg/m3。在PFC中有很多接触类型,由于岩土体一般具有一定的粘结性,因此在选择接触模型时,选择线性平行粘结模型来表征岩土体颗粒之间的相互作用和力学行为。适当调整颗粒大小和孔隙率,根据软件自带的参数标定程序,确定的抗浮锚杆拉拔试验颗粒流模型细观参数见表1。

表1 抗浮锚杆拉拔试验颗粒流模型细观参数Table 1 Mesoscopic parameters of particle flow model for anti-floating anchor pull-out test

2 单根抗浮锚杆拉拔模拟与分析

2.1 抗浮锚杆拉拔极限承载力的确定

为确定抗浮锚杆的极限承载力,通过对抗浮锚杆端头处施加三种不同的速度(0.1 m/s、0.2 m/s、0.5 m/s)进行拉拔试验,同时监测抗浮锚杆所受到周围岩土体的接触力,并通过仿真计算得出锚杆极限承载力时程曲线(见图2)。

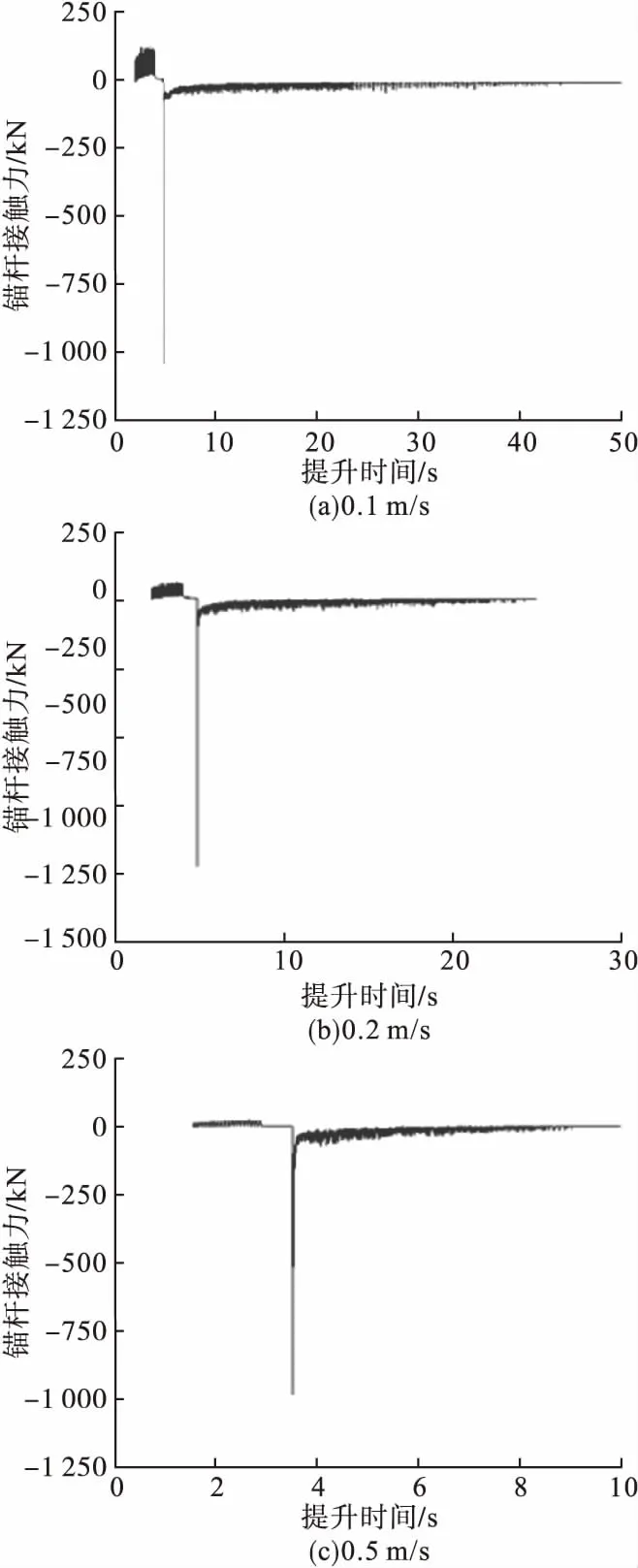
图2 不同拉拔速度下的极限承载力时程曲线Fig.2 Time curves of ultimate bearing capacity at different pulling speed

从图2可以看出,抗浮锚杆受到周围岩土体的接触力,即锚固界面上的摩擦力经历了缓慢增大-急剧增大-急剧减小-最终趋近于零的过程。抗浮锚杆在向上移动过程中,受到静摩擦力逐渐增大,该最大静摩擦力值即为抗浮锚杆在拉拔过程中的极限承载力。通过命令流监测模型中抗浮锚杆受到的接触力,在速度为0.1 m/s、0.2 m/s和0.5 m/s时,抗浮锚杆受到的最大摩擦力分别为1 050 kN、1 034 kN、1 068 kN,三个接触力相近。因此不同拉拔速度对锚杆的拉拔极限承载力影响不大,抗浮锚杆拉拔极限承载力取三者的最小值,并向下取整为1 000 kN。达到拉拔极限承载力时,抗浮锚杆周围岩土体中的颗粒速度云图、位移云图以及力链云图如图3所示。

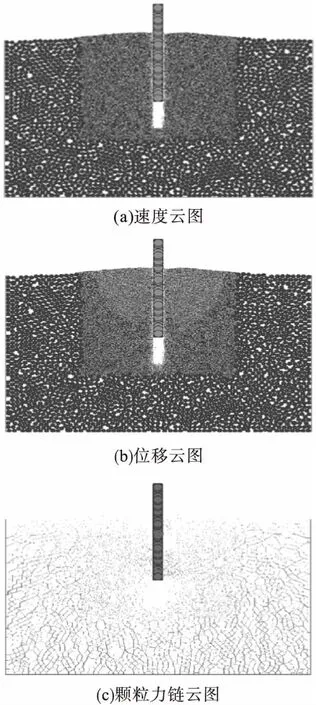
图3 不同拉拔速度下岩土体的颗粒速度、位移和力链云图Fig.3 Plots of particle velocity,displacement and force chain of geotechnical body under different pulling speed

由图3可知,在拉拔过程中,当抗浮锚杆达到拉拔极限承载力时,岩土体中的颗粒速度、位移均呈现V字型向上分布,与抗浮锚杆紧密接触的岩土体颗粒速度最大。当锚杆向上速度为0.1 m/s、0.2 m/s以及0.5 m/s时,与抗浮锚杆紧密接触处的颗粒最大速度分别为0.045 m/s、0.14 m/s以及0.38 m/s,最大位移在0.35 ～0.48 m。通过对岩土体颗粒接触力力链图分析可知,接触主要集中在抗浮锚杆底部的锥形区域,锚杆下部出现空白区说明该区域无接触,岩土体整体接触分布为围绕锚杆呈渐变式分布,由于岩土体重力与抗浮锚杆拉拔荷载的相互作用,使得上部岩土体接触力小,下部岩土体接触力大。

2.2 抗浮锚杆拉拔性能分析

在拉拔试验过程中需要对不同区域进行监测,以得出抗浮锚杆与岩土体颗粒作用的细观过程。通过PFC2D中的Measure功能建立不同位置的测量圆,测量圆的位置分布如图4所示。在靠近抗浮锚杆的一侧放置上、中、下3个测量圆,远离抗浮锚杆一侧的中部区域放置一个测量圆。

图4 抗浮锚杆颗粒流模型测量圆分布图Fig.4 Particle flow model of float-resistant anchor measuring circle distribution

2.2.1 竖向应力变化规律

通过对不同监测区域进行研究,得到三种不同速度下抗浮锚杆颗粒流模型轴向应力随计算时步的变化曲线如图5所示。从图中可以看出,在拉拔过程中,4个测量圆区域的轴向应力呈先增大后减小、最后逐渐趋近一个稳定值的趋势。其中靠近抗浮锚杆中部区域的岩土体颗粒轴向应力增大的最多,远离抗浮锚杆中部区域的岩土体颗粒轴向应力增大的最少。因此在拉拔过程中,靠近抗浮锚杆中部的岩土体受到的应力最大,越远离抗浮锚杆受到应力越小,最终抗浮锚杆全部拉出土体后,由于产生了一个空白区域,此时轴向应力从小到大顺序:近锚杆上部、近锚杆中部、近锚杆下部以及远锚杆中部。

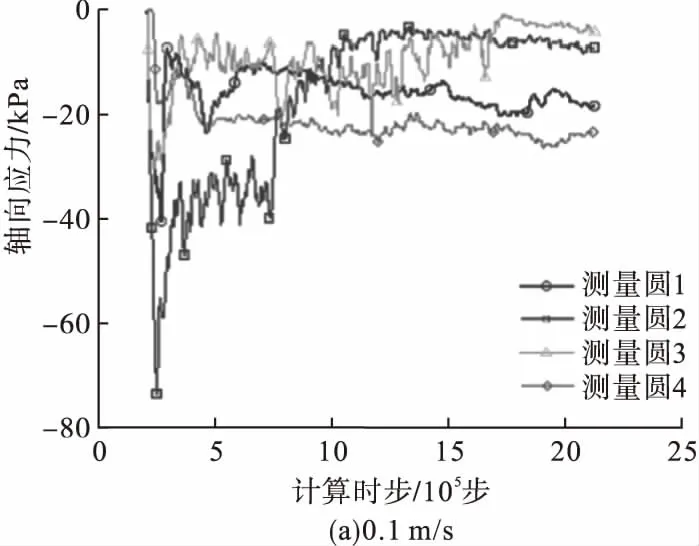
图5 不同拉拔速度下抗浮锚杆颗粒流模型轴向应力时程曲线Fig.5 Time course curves of axial stress in granular flow model of anti-floating anchor with different pulling speed

2.2.2 剪应力变化规律

通过对不同监测区域进行研究,得到三种不同速度下抗浮锚杆颗粒流模型剪应力随计算时步的变化曲线如图6所示。

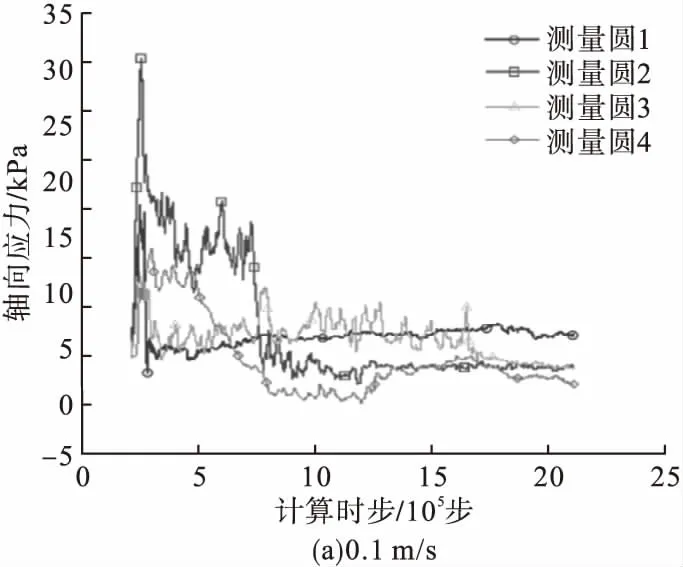
图6 不同拉拔速度下抗浮锚杆颗粒流模型剪向应力时程曲线Fig.6 Time course curves of shear stress in granular flow model of floating anchor with different pulling speed

从图6可以看出,在拉拔过程中,4个测量圆区域的剪应力呈先增大后减小,最后逐渐趋近一个稳定值的趋势。其中靠近抗浮锚杆中部区域的岩土体颗粒剪应力增大的最多,远离抗浮锚杆中部区域的岩土体颗粒剪应力增大的最少,因此在拉拔过程中,靠近抗浮锚杆中部的岩土体受到的应力最大,越远离锚杆受到应力越小,最终锚杆全部拉出岩土体后,由于产生了一个空白区域,此时剪应力从小到大顺序:近锚杆下部、近锚杆中部、近锚杆上部以及远锚杆中部。

2.2.3 孔隙率变化规律

通过对不同监测区域进行研究,得到三种不同拉拔速度下抗浮锚杆颗粒流模型的孔隙率随计算时步的变化曲线如图7所示。从图7可以看出,在拉拔过程中,各区域的孔隙率变化呈先增大后减小,最后趋于一个稳定值的趋势。当抗浮锚杆全部拔出岩土体后,孔隙率计算结果从大到小依次为近锚杆上方、近锚杆下方、近锚杆中部以及远离锚杆中部。分析原因主要是由于岩土体在抗浮锚杆上部和下部受到了扰动破坏,导致孔隙率增大,而近锚杆中部区域颗粒在较大应力下更加紧密,远离锚杆中部受到的扰动较小,变化也较小。

图7 不同拉拔速度下抗浮锚杆颗粒流模型孔隙率时程曲线Fig.7 Time course curves of granular flow model porosity of float-resistant anchors under different pulling speeds

3 单根锚杆拉拔时群锚的颗粒流模拟

本模型的打桩方式为隔桩跳打,在群锚颗粒流模拟时只对中间的抗浮锚杆进行拉拔(见图8),以此探究该工况下的岩土力学性质。

图8 单独拉拔中间抗浮锚杆的群锚颗粒流加载模型Fig.8 Group anchor particle flow loading model for individually drawn intermediate anti-floating anchors

通过PFC2D建立只拉拔中间抗浮锚杆的群锚颗粒流模型,对两侧锚杆及附近岩土体进行力学分析,监测拉拔过程中相邻锚杆与不同土体区域的轴向应力、切向应力、轴向应变、切向应变以及孔隙率。以桩距为4倍抗浮锚杆直径为例,确定该种工况下的拉拔极限承载力,同一提升速度(0.5 m/s)下监测的轴向应力、剪向应力。

拉拔过程中需要对相邻抗浮锚杆以及岩土体不同区域进行监测,以得出抗浮锚杆与相邻锚杆以及岩土体颗粒作用机理。通过PFC2D中的Measure功能建立不同位置的测量圆,设置在靠近中间锚杆的左右两侧,分别布置上、中、下三个测量圆;还有外侧左右两侧中部也同样布置上、中、下三个测量圆。通过对测量圆区域范围内的轴线应力应变、孔隙率以及相邻锚杆的位移以及接触力等指标进行监测,结果如图9所示。

图9 单独拉拔中间抗浮锚杆群锚颗粒流模拟结果Fig.9 Simulation results of particle flow for group anchors of individually drawn intermediate anti-floating anchors

由图9可知,当中间抗浮锚杆向上拉拔、两侧锚杆不动时,轴向应力与剪向应力同样呈现先增大后减小,最终趋于稳定,轴向应变与剪向应变先在零刻度附近波动,随后保持稳定的趋势。分析原因是在拉拔过后,在中间锚杆下部出现脱空区,出现脱空的区域锚杆与土体之间的相互作用消失,并且两侧锚杆也会对土体产生保护作用,导致剪向应力与轴向应力产生这种现象,并且由下到上土体的轴向应力及剪向应力依次降低,这主要是由于上方土体产生的位移以及速度更大所导致的。

不同区域的孔隙率监测结果如图10所示。由图可知,不同位置的孔隙率先逐渐增大最后趋于稳定。对于不同位置的孔隙率,外侧的岩土体孔隙率要比内侧的孔隙率小,分析原因是在拉拔过程中,内侧岩土体在相邻两根锚杆的上拉作用会导致岩土体变得疏松,相比于外侧孔隙率更大;外侧岩土体由于只受到一根锚杆的向上作用,使得原来的岩土体性质变化不大。最大的孔隙率为0.194,位置为中间上部岩土体,最小的孔隙率为0.163,位置为边缘下部岩土体。

图10 孔隙率变化时步图Fig.10 Time-step diagram of porosity change

为了研究在向上拉拔中间锚杆的过程中对相邻锚杆的影响,使用PFC2D软件来实时监测两侧锚杆的接触力,及时获得监测结果以此了解中间锚杆对相邻锚杆产生的影响。

随着中间抗浮锚杆的不断拉拔,其产生的作用力会导致相邻锚杆的接触力逐渐上升,在中间抗浮锚杆达到300 kN时,相邻锚杆的接触力达到最大值(见图11)。随着中间抗浮锚杆的不断向上拉拔,接触力开始迅速减小,最终趋于零,这表明中间锚杆产生的作用力会随着中间锚杆的移动而消失。

图11 相邻锚杆接触力变化时步图Fig.11 Time step diagram of the change in contact force of adjacent anchor rods

4 结 论

(1)对于轴向应力,靠近抗浮锚杆中部的岩土体受到的应力最大,越远离锚杆受到的应力越小。对于孔隙率,孔隙率从大到小的区域依次为近锚杆下部、近锚杆中部、近锚杆上部以及远锚杆中部。

(2)当中间抗浮锚杆向上拉拔、两侧锚杆不动时,轴向应力与剪向应力同样呈现先增大后减小、最终趋于稳定的变化规律。

(3)相邻的锚杆在中间锚杆不断上拔的过程中,接触力循环上升并最终达到最大值,随后迅速减小。由于锚杆之间的距离较近,因此出现了群锚效应,单锚的抗拔力损失明显。此外,早期少数锚杆变形过大失效后,浮力荷载转移到了临近锚杆导致连锁反应,是引起锚杆失效的原因。