基于RF-BP 组合模型的混合型基金预测研究*

何英洁 王世民

（北京工商大学电商与物流学院 北京 100048）

1 引言

混合型基金作为开放式证券基金的一种，因其复杂多变的组织形式和介于股票和债券之间的投资风险受到广大人名群众的追捧。同时在推动我国经济发展之中，相对于股票的不稳定性而言，数量庞大的混合型基金以其灵活多变的投资风格也发挥着更大的作用。基金市场作为一个开放性的大市场，不仅受到系统性的风险，还受到投资者心理，基金公司财务状况等非系统性的风险。因此，大多数的基民在投资基金时，往往很难选择，或者人云亦云，造成了巨大的损失，也造成了我国证券市场的不健康发展。

混合型基金净值波动的研究主要集中在对基金预测方法的应用上，如于立媛、宋锋把灰色模型与马尔科夫链组合起来，其组合模型要优于单一的灰色模型［1］；向莹、王雅萍把ARIMA 模型应用到华安上证180ETF、预测效果较好［2］；肖国荣证明了改进型BP 神经网络的预测精度要优于传统的BP 神经网络［3］；翟育明、邹亚平、周俊文、冯旖旎提出将遗传算法（GA）与传统BP 神经网络组合成一种自适应遗传神经网络模型来对基金净值进行了预测［4］；何树、红吴迪、张月秋证明了RBF神经网络的预测效果要优于BP 神经网络［5］；崔琳证明了PSO优化后RBF 神经网络模型要优于传统的BP、RBF模型［6］。乔宝明、黄晶、范雯将改进的小波阈值理论与自回归模型相结合，其预测效果要优于单一的自回归模型［7］；景阳将小波分解理论与多元回归算法相结合成一种新的基金预测模型，其预测效果要好于传统ARMA、小波去噪自回归模型［8］。综上所述，这些方法主要集中在对方法的改进以及应用上，但是实际的应用场景并没有考虑。基金的种类繁多，指标和方法的选择不当会影响预测的精度，甚至是导致预测失败。

在结合前人对于基金净值预测研究的基础上，提出将随机森林算法与改进型的BP神经网络组合成RF-BP 模型来对混合式基金进行预测。结果证明该模型对于混合型基金净值的预测要优于传统的BP神经网络。

2 基金预测模型设计

2.1 特征选择算法

随机森林算法能够处理高维度的数据，且具有较强的泛化性，能够兼顾基金净值各影响指标之间的耦合作用，消除冗余度大和不相关的属性。采用随机森林算法从构建的特征库中，能够筛选出对基金净值有重要影响的指标。

选择分类回归树（CART）作为决策森林的基树。采用MSE（均方误差）作为结点分裂的依据来搭建随机森林做特征重要性度量。计算方法如下［9～10］：

1）对于随机森林中的每一棵回归树，使用相应的OOB（袋外数据）数据来计算它的误差（预测值与真实值之间的误差），记为error1。袋外数据指的是，每次建立决策树时，以重复抽样的方式得到一批数据用于训练决策树，最终会留下大约1/3 的袋外数据没有被利用。

2）随机对袋外数据D2的所有样本的特征加入噪声干扰（随机改变样本在特征x 处的值），再次计算袋外数据误差，记为而error2。

3）假设我们构造的随机森林有n 棵基树，则特征的重要性为

feature_importances=∑(abs(error2-error1))/n

用它来判断每个特征的重要性，是因为在加入随机噪声后，袋外数据（OOB）的准确率会大幅度减少，减少越多说明对预测结果的影响越大，就越重要。

4）利用上述方法计算出所有特征的重要性，并按升序进行排列，然后采用后向迭代的方法，每次去掉一个重要性最低的特征，再对剩余的特征进行重要性评估，重复进行上述操作，直到遍历完所有特征，然后选取袋外误差最小（OOB_SCORE_分数最高）时的特征，作为最后选定的指标体系。

2.2 BP神经网络

利用随机森林对特征进行提取后，采用BP 神经网络作为预测模型，相较于ARIMA、灰色模型、回归模型［3］，其能够较好地拟合出基金净值的波动规律。

BP 神经网络是一种按预测误差不断进行反向调节的多层前馈神经网络。其结构如图1所示。

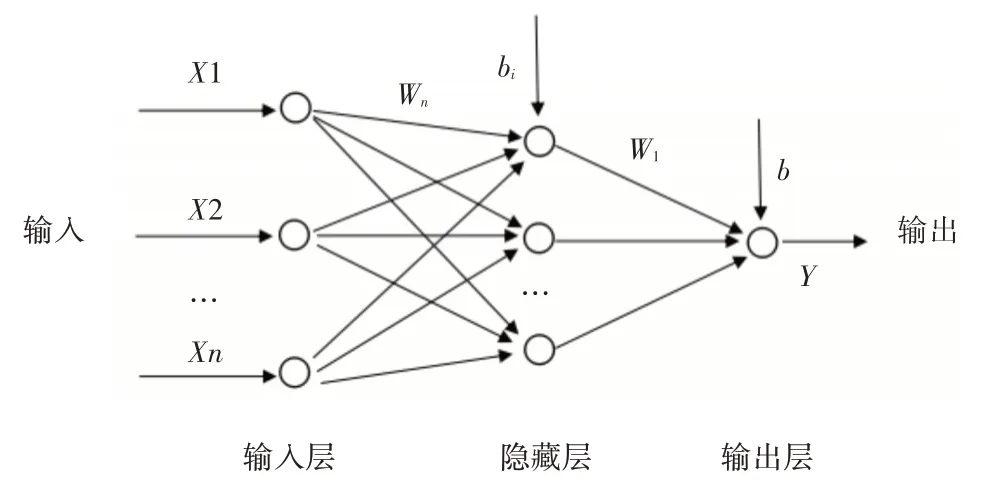
图1 BP神经网络结构图

2.3 BP神经网络算法及其改进

针对传统的BP算法，训练时间长、梯度消失造成训练失败等问题，本研究采用改进型的BP算法，以变学习率动量梯度下降算法为优化算法，TANSIG 为输出层到隐层的激活函数，PURELIN 为隐层到输出层的激活函数，经证明，在隐层采用S 型函数，在输出层采用线性函数具有逼近任何连续函数的特性。其算法又分为前向传递和后向传递两部分，如过程1）、2）所示。设有12个特征变量Xi（i=1，2…12），一个输出Y，共有（Xik，Yk）（k=1，2，…N）个样本，隐藏层节点输入O（j（1）），输出为Oj（j 为隐藏层节点数），隐藏层和输出层偏置bj和b2。

1）前向传递过程如下：

隐藏层输入为

隐藏层输出为

输出层为

隐层激活函数（TANSIG）

输出层激活函数（PURELIN）

平方误差公式为（MSE）［11］

其中Yk（t）为网络实际输出。可具体表示为

2）反向传递过程（根据链式法则，损失函数对各个需要更新的参数求偏导，反复迭代，直至损失误差达到预期值）：

可以推出，隐藏层到输出层权重更新公式以及输出层到隐藏层的为

对偏置b 采取同样的更新方式，这里不再赘述。

改进在于对反向求导过程，选择变学习率动量梯度下降算法。动量梯度下降算法降低了网络对于误差曲面局部细节的敏感性，而且把动量项作为阻尼项，在综合考虑上几次权值的基础上，减小了学习过程中的振荡趋势。同时，在动量梯度下降算法中引入自适应学习速率，根据所处的不同误差曲面区域，学习率能够实时自主调节，降低训练次数，能够避免跳出最佳极小值的情况。对比原始的梯度下降法，变学习率动量梯度下降算法能够克服在训练过程中发生的震荡，且具有训练时间快、泛化性强，不易陷入极小值等特点，具体算法又可分为两部分。

1）增加动量项：

W（k）为连接权系数；Dk=-∂Ek/∂Wk为k 时刻的负梯度；D（K-1）是k-1 时刻的负梯度，u 为学习速率，u＞0；a是动量因子。

2）自适应调节学习率：

设一初始学习率u，若经过一批次权值调整后使总误差E 变大，则本次调整无效，且μ(k+1)=βμk(β<1)；若经过一次权值调整后使总误差E变小，则本次调整有效，且μ(k=1)=θμk(θ>1)。

3 实例仿真分析

3.1 初步特征选择

在参考王敏基于BP神经网络对基金净值预测研究［13］；张纲等从基金经理特征和基金公司特征的双重视角下对基金业绩的研究［14］；张洁琼、杨孔雨基于面板数据的开放式基金净值影响因素的研究［15］；朱冰、朱洪亮对积极开放式基金的规模与收益的关系研究［16］；高金窑、张晓雪对我国证券投资基金预测能力的决定因素研究［17］，以及国泰数据库、天天基金、晨星网对于相关数据的解读的基础上，初步选取了基金份额净值、基金份额累计净值、基金份额复权单位净值、基金份额累计净值周增长率（%）、基金份额复权单位净值周增长率（%）、沪深300 指数、持股比例、持债比例、现金比例、净资产规模（亿元）、基金换手率（%）、持仓行业集中度（%）、上一周净值、上一周累计净值、基金份额复权单位净值'（上一周）、收益率标准差（%）、Sharpe率、市场组合平均收益率（%）、Beta 值、詹森指数-Alpha 值、特雷诺指数（%）、TM 模型择时能力gamma、TM 模型选股能力alpha'、CL 模型熊市择时能力gamma1'、CL 模型牛市择时 能 力gamma2'、CL 模型择时能力gamma'、CL 模型选股能力alpha'、CPI（居民消费价格指数），28 项作为研究基金净值波动的指标库。

3.2 特征筛选

如图2 所示，初步选取的28 个特征，进一步采用随机森林回归做出的特征重要性图表（以对混合型A（平衡）基金第一次迭代为例）。

图2 特征重要性（混合型A（平衡）基金）

为消除研究样本的单一性这里增选混合型（偏股）B、（偏债）C 两只基金进行对比和泛化研究，依据袋外数据误差最小（OOB_SCORE_分数最高）准则，见图3，发现当特征数为12 时，OOB_SCORE_分数最高，预测结果的准确性主要与基金份额净值（X1）有关，其次是上一周的净值（X2）、市场组合平均收益率（X3）、基金换手率（X4）、基金份额累计净值（X5）、基金份额复权单位净值（X6），CL 模型熊市择时能力（X7）、上一周累计净值（X8）、沪深300指数（X9）、特雷诺指数（X10）、收益率标准差（X11）、居民消费价格指数（X12）。

3.3 数据预处理

以混合型A（平衡）基金为例，参照（偏股）B、（偏债）C两只混合式基金，截取从2013年3月22号到2019年6月30号共323周的数据作为样本，最终筛选出3.2小节所示的（X1～X12）共12个特征作为BP神经网络的输入变量。

由于选取的特征具有不同的物理意义和量纲，为使训练伊始各输入分量同等重要，避免输入数据落入饱和区域，本文将原始数据利用式（12）进行［0，1］归一化［4］。

3.4 实验方法选择

选取已处理数据中的前315 周数据为训练集，余下8 周为测试集，以X1～X12为输入变量，以Y为输出变量。在BP 神经网络训练中，隐藏节点的选取参考经验式（13）［11］：

其中：n 为输入节点数；m 为输出节点数，a 为1～10之间的整数。本文中n为12，m 为1，则节点的取值范围是［4，13］，分别取该范围内的值建立神经网络，其他参数，学习率设为0.25，训练次数为10000，精度设为0.0012，动量因子设为0.95。经验证，当节点为4时，预测值的均方误差最小为0.00678。

本研究采用时间移动仿真法，每次仅预测一周，预测完后，该周加入训练，从而预测下一周，直至第八周预测结束，可以充分考虑到基金净值近期波动影响因素，减小预测误差［11］。

3.5 实证结果的分析

利用Matlab R2019a 软件编程实现RF-BP 组合模型，对混合型A（平衡）基金进行了预测并与参考文献［13］中固定指标的传统BP神经网络进行了对比。同时对偏股型B 和偏债型C 两只混合型基金进行了预测。

1）混合型A（平衡）基金的预测结果及分析RF-BP 模型与传统BP 预测的拟合效果如图4 所示。

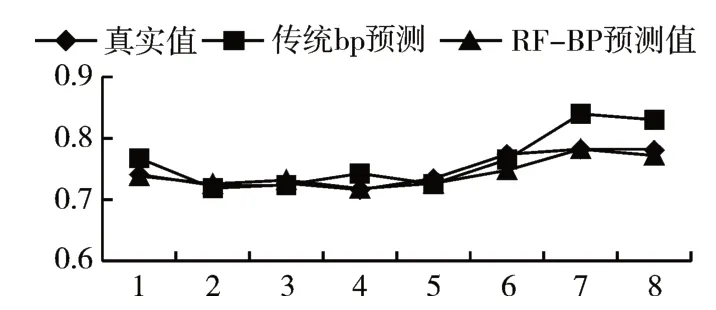
图4 改进型BP与BP预测拟合效果图（混合型A（平衡）基金）

RF-BP组合模型相较于传统的BP算法对混合型A基金净值的预测有明显的优势，结果验证其平均绝对误差降低了340%。

2）模型的泛化性和样本的多样性

增选偏股型B 和偏债型C 两只混合型基金的预测效果图，如图5、6 所示，发现RF-BP 算法要优于传统BP算法。

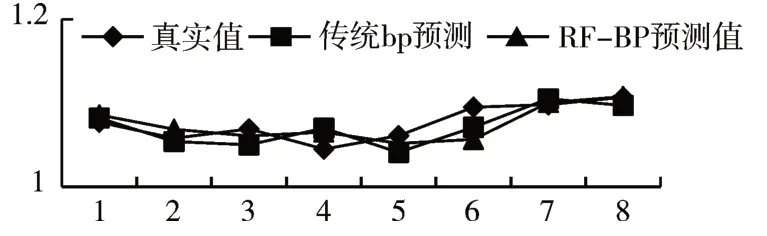
图5 预测结果对比（混合式B（偏股）基金）

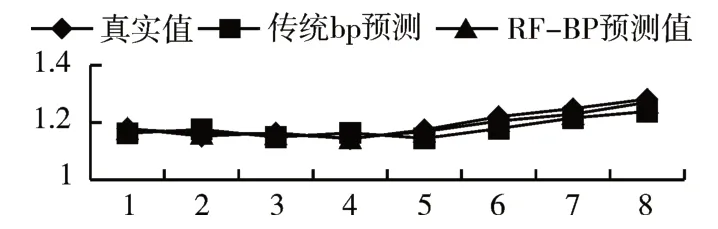
图6 预测结果对比（混合式C（偏债）基金）

综上所述，通过构建指标库，并利用随机森林对特征进行优化与改进BP 神经网络的组合（RF-BP 模型）要优于传统固定指标的BP 算法，提高了方法的普适性，也提高了模型的预测精度以及泛化能力，能够较好地预测不同混合型基金净值的变化，预测值与真实值之间基本吻合，平均绝对误差基本上控制在2%以内。

4 结语

针对前人单纯基于BP、RBF、ARAMA 等方法的组合改进应用，存在收敛速度慢，陷入极小值，效果不稳定以及特征与样本数不满足要求等问题，在构建特征库，增加样本量的基础上，提出将随机森算法与改进型的BP 神经网络组合成RF-BP 模型。经实证分析，该模型对混合型基金具有较高的预测精度，具有较好的泛化性、普适性等，大幅度缩减了训练时间，能为基民合理选择混合式基金提供一定的数据参考。