基于粒子群优化支持向量机的癫痫发作预测*

刘金森 黄炜嘉 李效龙

（江苏科技大学电子信息学院 镇江 212100）

1 引言

癫痫是一种危害极大的神经系统疾病，具有突发性与反复性，严重影响了病人的日常生活。越来越多的研究表明，癫痫发作具有可预测性［1］。如果能够在癫痫发作之前发出警报，提醒病人家属或者医生对病人采取相应措施来抑制癫痫发作，就能够减缓癫痫病人的痛苦，从而降低癫痫发作给患者带来的危害。目前，癫痫发作自动预测已经成为脑电疾病研究领域的热点问题。

癫痫发作分为发作前期、发作期、发作后期和发作间期四个阶段［2］。癫痫预测的主要目标是对癫痫发作前期与癫痫发作间期的脑电信号进行区分，识别出发作前期信号并发出预警，进而达到癫痫预测目的。

对于发作前期与发作间期的二分类问题主要分为特征提取和模式识别两个部分。在癫痫病人的脑电信号特征提取方面，学者们做了大量的研究工作，主要分为以下四类：1）时域方法：均值、标准差［3］、Hjorth 复杂度［4］等；2）频域方法：功率谱［5］；3）时频分析方法：短时傅里叶变换［6］、小波变换［7］、小波包变换［8］、经验模态分解［9］；4）非线性动力学方法：最大Lyapunov 指数［10］、熵［11］。时域分析方法主要是分析信号的几何特性，如对癫痫棘波、尖波等特征波形进行分析；频域分析主要是通过傅里叶变换、Weich 方法、AR 模型参数方法获得信号的功率谱，将脑电信号各频段的功率、相对功率、绝对功率等作为特征进行研究。然而，时域和频域方法都只针对信号单一角度进行度量，且通常需要假设脑电信号为平稳信号，这与脑电信号的非平稳性相矛盾，小波包变换具有良好的正交性和局部特性，可以对信号进行多尺度、多分辨分析，非常适合于脑电信号等非平稳信号的分析研究。

随着机器学习的发展，涌现出越来越多的分类方法，应用在脑电信号分析领域的有K-近邻、支持向量机、线性判别式以及人工神经网络等［12］。其中，支持向量机是应用最多的分类方法，它不涉及人工神经网络中的网络结构选择，并且避免了“维数灾难”［13］。目前癫痫预测方面涉及到支持向量机作为分类方法，参数设置多采用人工经验选取和网格搜索方法［14］，凭经验选取具有一定的随机性，网格搜索在较大范围内进行搜索，存在耗时较长等问题。因此，本研究采用小波包变换和支持向量机结合来构建癫痫发作预测模型，同时为提高分类准确率、减少计算时间，采用粒子群算法对支持向量机的参数进行优化。

2 方法和原理

2.1 小波包系数能量

小波包变换是轴承故障特征提取中常用的信号分析方法，近年来也越来越多地应用于脑电信号的处理当中［15～16］。癫痫发作前期与发作间期的脑电信号不同频段具有不同的变化趋势，应用小波包变换的自适应性可以很好地提取出信号不同频段特征。

小波包变换满足如下的二尺度方程：

其中：hk和gk为一组正交滤波器，满足gk=(-1)nh1-k。

Mallet小波包快速分解算法描述如下：

信号的时域能量为

由帕斯瓦尔定理［16］可知：信号在时域能量上的能量与小波包系数能量相等，因此，信号各频段的能量可表示为

其中：j代表小波包分解层数，k表示信号频率成分，N 代表信号采样点数，Cj,k代表小波包分解系数。

为了消除量级对数据的影响，本文采用相对能量作为特征，具体表示如下：

其中：Ej,k代表信号各频段能量值，代表信号各频段总能量值。

2.2 支持向量机

支持向量机主要思想如下：首先通过一个非线性映射Φ(x)将y类脑电信号特征x映射到高维空间，然后找到一个超平面使得所有的点到超平面的距离大于一定值［17］。算法具体步骤如下。

1）超平面的构造归结为凸二次规划问题：

其中：w为超平面法向量，C>0 为惩罚参数，ξi≥0为松弛变量，b为超平面的偏置向量。

2）利用拉格朗日函数求目标函数极值，设拉格朗日函数为

其中：0 ≤αi≤C为Lagrange系数。

3）对式（7）求解最优化问题，得到最优解：

2.3 粒子群算法优化支持向量机

粒子群算法是基于对鸟类捕食行为进行建模衍生出来的一种智能优化算法。该算法把群体中的个体视为空间中的点，具有一定的初始速度，在此过程中依据自身和同伴的飞行经验对自身的飞行速度、前进方向进行动态调整［18～19］。

粒子的速度和位置更新公式如下：

式中：xi=(x1,x2,…,xn)表示粒子在N 维空间的位置，飞行速度表示为矢量vi=(v1,v2,…,vn)表示粒子在N 为空间位置，pbest表示粒子i的个体最优位置，Gbest表示粒子群的全局最优位置；c1，c2为常数，表示学习因子；γ1,γ2∈( )0,1 ；w表示惯性因子。

粒子群算法优化支持向量机的流程图如图1所示。

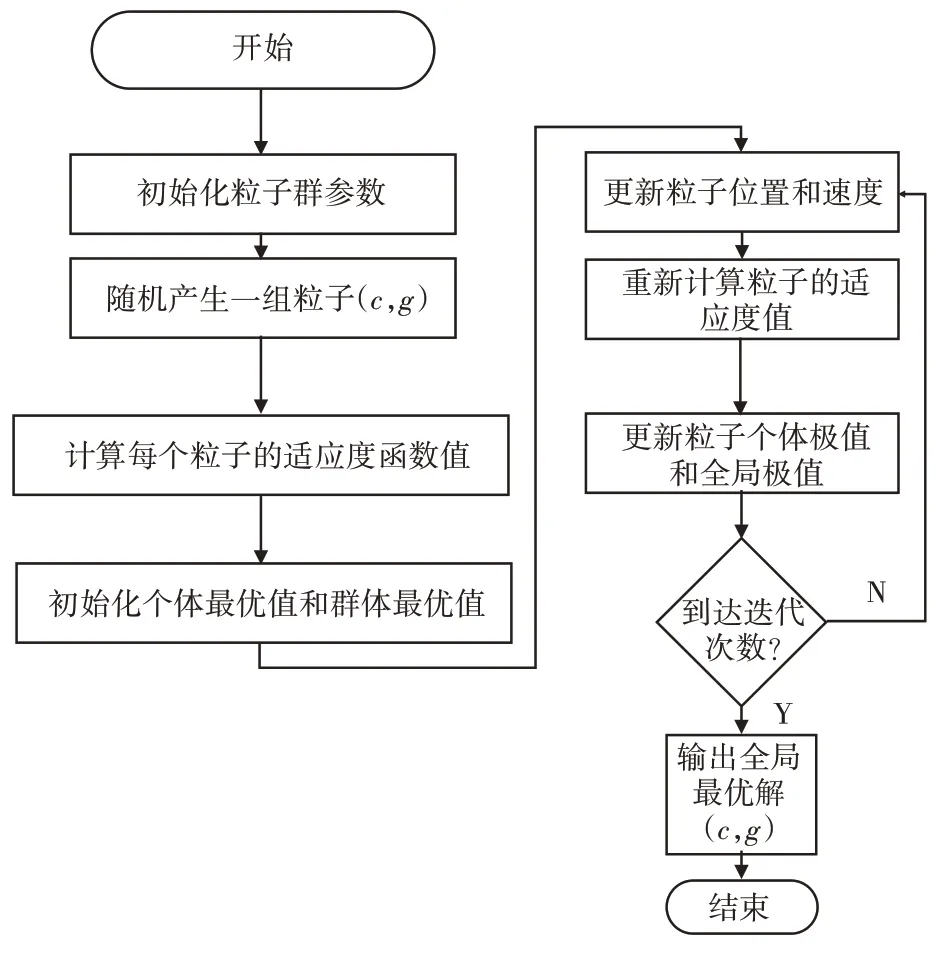
图1 PSO优化SVM算法流程图

其算法具体流程如下：

1）初始化参数：种群规模N、最大迭代次数i、惯性因子w、参数c、σ的变化范围；

2）根据种群规模随机产生一组粒子(c,σ)；

3）适应度函数为十折交叉验证计算出的平均准确率，根据适应度函数分别计算每个粒子的适应度函数值；

4）每个粒子的适应度函数值即为当前个体最优值，比较所有粒子的个体最优值，值最大的作为全局最优值，对应粒子位置(c,σ)作为全局最优位置；

5）根据式（12）和式（13）更新粒子速度和位置；

6）根据更新后的粒子位置重新计算粒子适应度函数值；

7）比较更新后的适应度值与个体极值、群体极值，若优于更新前，则用更新后的值进行替换；

8）判断迭代次数是否小于Tmax，若达到，则输出当前全局最优解(cbest,σbest)，否则返回步骤5）。

本文参数设置如下：种群规模N=20，最大迭代次数Tmax=200，惩罚因子c最小值cmin=0.1，最大值cmax=100，核函数σ的最小值σmin=0.01，最大值σmax=1000 ，惯性因子w=1，c1=1.5，c2=1.7。

2.4 输出结果后处理

为了减少错误警报，还需要对SVM 输出结果进行判决分析。本文提出一种基于阈值的判断方法，具体过程如下：

1）统计每隔1min 的时间窗，支持向量机的输出为发作前期的标签数目：

其中：numpreictal[t]表示第t 个时间窗内的发作前期样本个数；labeli表示第i个样本的SVM输出标签。

2）使用numpreictal[t]的值可以判断在过去的这1min 内信号处于发作前期还是发作间期，具体如下：

其中：P值为一个阈值，P∈[1,6]，6表示以10s为窗口大小，1min 内的窗口数。当numpreictal[t]≥p时，state[t]=1，即认为在过去的1min内，信号处于发作前期状态；否则处于发作间期。

3 实验结果与分析

3.1 实验数据与处理

本文采用CHB-MIT 癫痫开源数据库（https：//www.physionet.org/content/chbmit/1.0.0/），该数据库记录了23 位癫痫病人的数据，所有信号以16 比特分辨率进行采样，采样频率为256Hz。

根据本次实验数据集的特点以及相应实验验证，本文将每次癫痫发作前10min 定为发作前期。同时为了实现更快地对数据进行处理，减少计算时间，本文采用滑动窗口技术对信号进行分段处理。发作前期、发作间期样本均采用10s 无重叠窗口，窗口步长为10s。

3.2 特征提取结果与分析

已有实验表明Daubechies 小波家族对脑电数据具有很好的处理效果，经试验采用db5 小波对信号分析，五层分解后共得到25=32 个频率成分，各节点及其频率成分如表1所示。

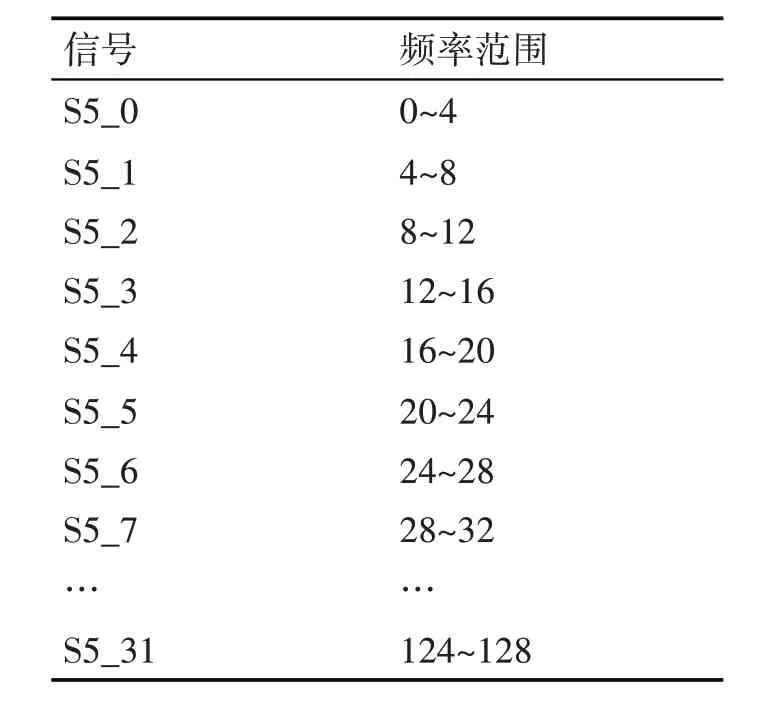
表1 小波包变换分解结果

脑电的分析范围多为0 ～32Hz，所以对分解后得到前8个频段进行分析，其相应频谱如图2所示。

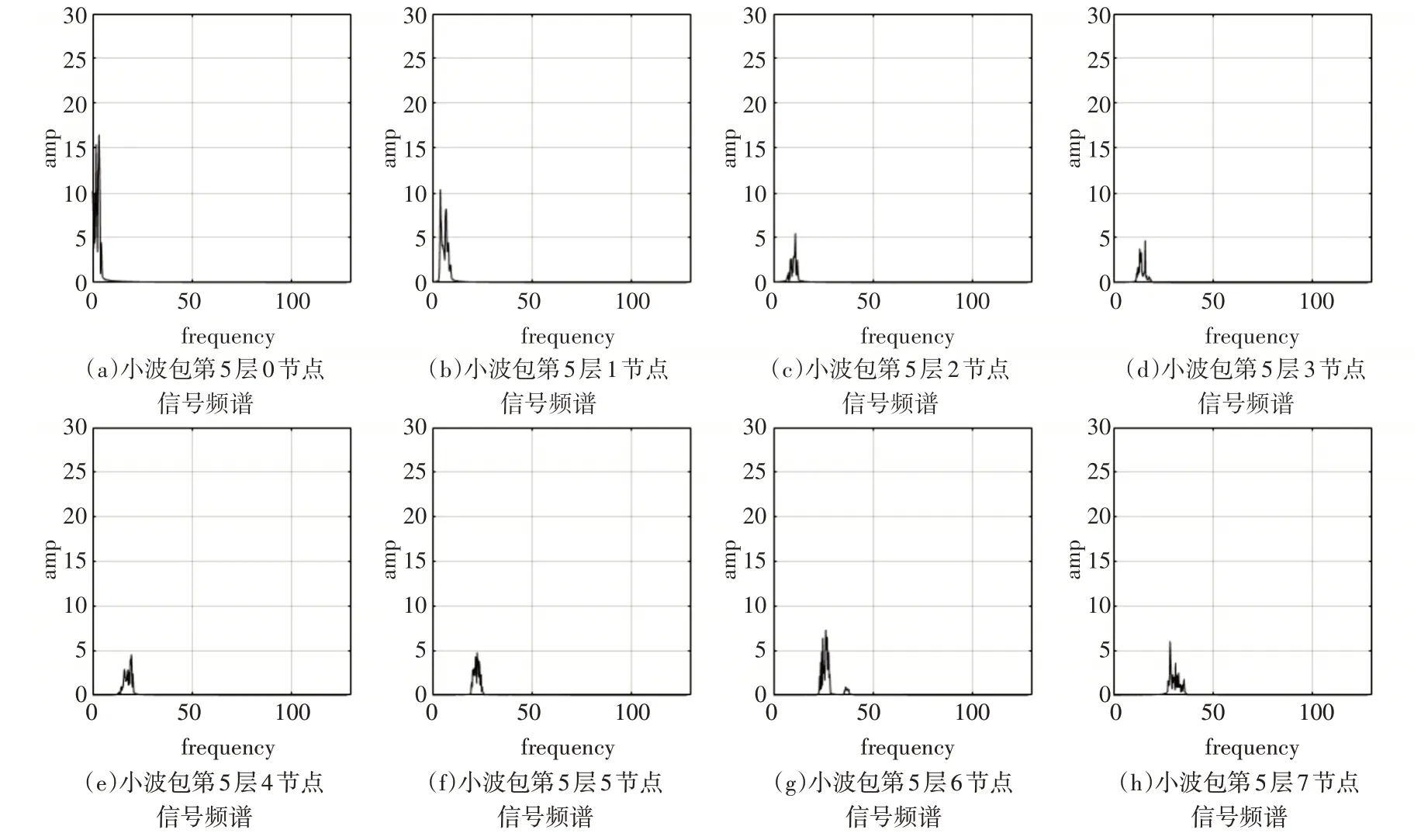
图2 第五层前8个节点频谱图

对经过小波包变换分解后各频段分解系数求取相对能量值来反映病人在发作前期、发作间期的信号变化情况，以第一位病人的第一次发作为例，图3、图4分别为该病人第一次发作前期一个10s窗口的小波包系数相对能量情况。

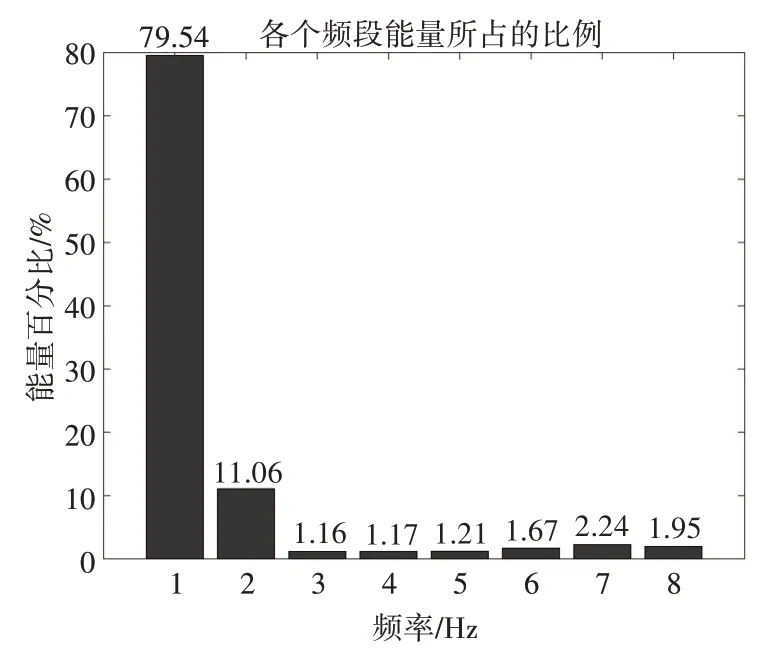
图3 发作前期小波包系数相对能量

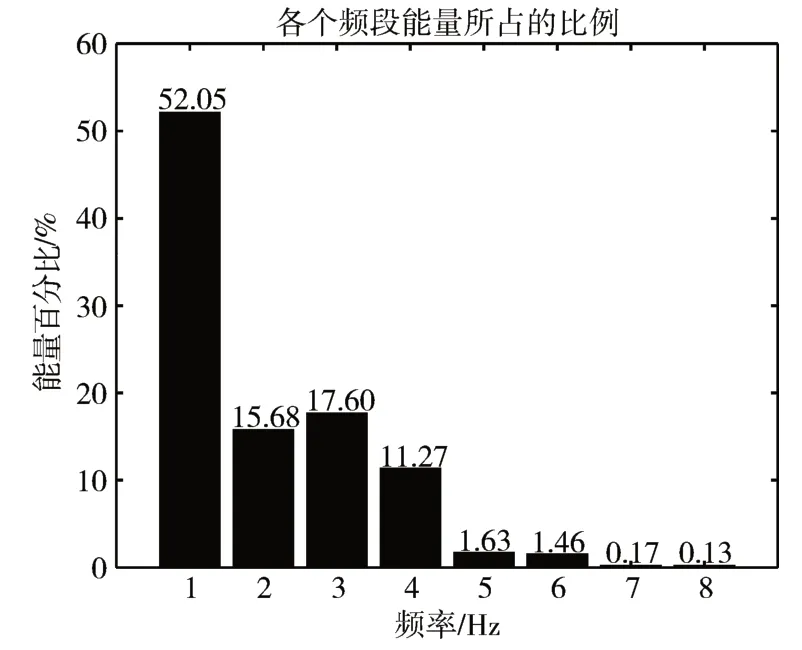
图4 发作间期小波包系数相对能量

通过对比两图，可以发现发作前期与发作间期的小波包系数能量占比有较为明显的差异，癫痫发作前期各频段能量由大到小依次为S5_0、S5_1、S5_6、S5_7、S5_5、S5_4、S5_3、S5_2，癫痫发作间期各频段能量由大到小依次为S5_0、S5_2、S5_1、S5_3、S5_4、S5_5、S5_6、S5_7。结果表明，小波包系数能量比值能够很好地反映发作前期与发作间期脑电信号不同频率的变化情况，由此证实了小波包系数相对能量作为特征区分两类信号的有效性。

3.3 识别结果与分析

本文选取5 位病人前两次发作前期10min、发作间期10min 的脑电数据，对样本数据进行特征提取。将其构成240×8 维的特征向量作为训练数据。选择第三次癫痫发作提取出来的特征向量作为测试数据进行分析。得到粒子群优化支持向量机的适应度曲线如图5所示。

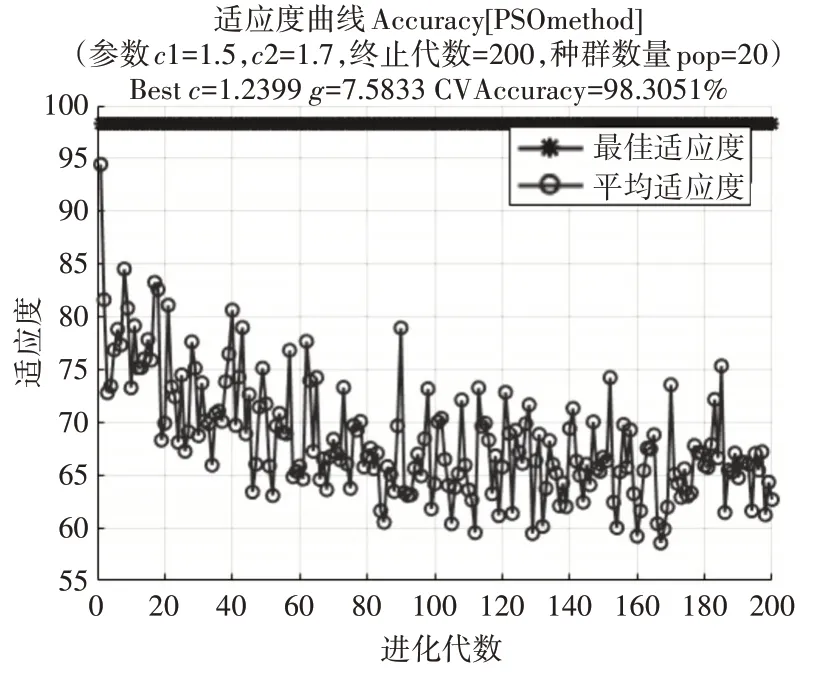
图5 粒子群优化算法适应度曲线

从图5 中可以看出经过200 次迭代处理，寻找得到的最佳c 和g 组合为（1.2399，7.5833），训练样本交叉验证准确率为98.3051%。

为了验证粒子群算法优化的有效性，本文设计了支持向量机随机参数选择和网格搜索两种方法进行对比实验。其中网格搜索范围设置为c,σ∈( 2-8,28)，步长大小设置为0.8。图6 为网格搜索优化支持向量机参数选择等高线图。

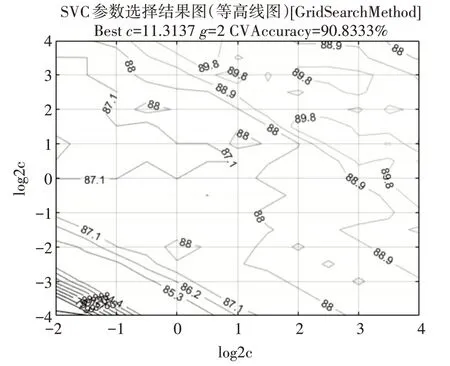
图6 网格搜索等高线图

从图6 中可以看出，该方法寻找到的最优参数组合为（11.3137，2），对于测试集样本的准确率为90.8333%。三种方法的准确率、所需时间以及寻找到的最佳参数组合具体如表2所示。

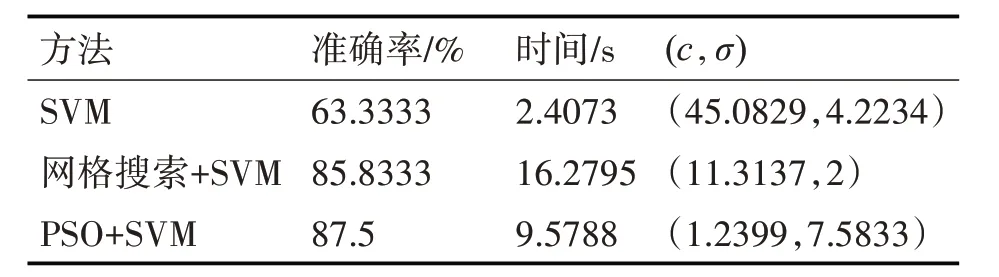
表2 三种方法性能比较

从表2 中数据可以看出，随机参数选方法虽然耗时较短，但分类效果最差，分类准确率只有63.3%；网格搜索方法的分类准确率与粒子群算法相近，但是耗时却约为粒子群优化算法的两倍，这对于计算速度要求较高的癫痫发作预测系统来说，显然不太适合。而粒子群优化算法在处理速度和识别准确率方面均达到较好效果，所以验证了本文方法的有效性。

3.4 癫痫发作预测结果与分析

图7 为对第1 位病人的第三次发作预测结果，时间选取为距离癫痫发作前的10min。其中图（a）、图（b）、图（c）、图（d）分别为发作前期原始信号时域图、支持向量机输出结果、阈值决策结果、发作前期处理后时域图。横轴为时间，间隔为10s，即为本文采用的滑动窗口大小。

从图7（b）中可以看出，支持向量机在第10s 输出为0。如果不采用阈值决策方法对输出结果进行处理，该段信号就会被判定为发作间期，从而不会发出预警，这增加了癫痫预测系统的误报率。若采用本文的后处理方法，如图（c）所示对每隔1min的6 个输出结果进行阈值决策，阈值P 取为4。0～1min 支持向量机输出3 个1，小于阈值4，经决策后判决为0；2min～3min 支持向量机输出4 个1，等于阈值4，经决策后判决为1，即系统认定为发作前期，在3min这一时刻发出预警。

表3 为5 名癫痫病人的实验预测结果，平均准确率为83.67%，平均敏感性为75.34%，平均特异性为92%，平均误报率为0，平均预测时间为6.8min。

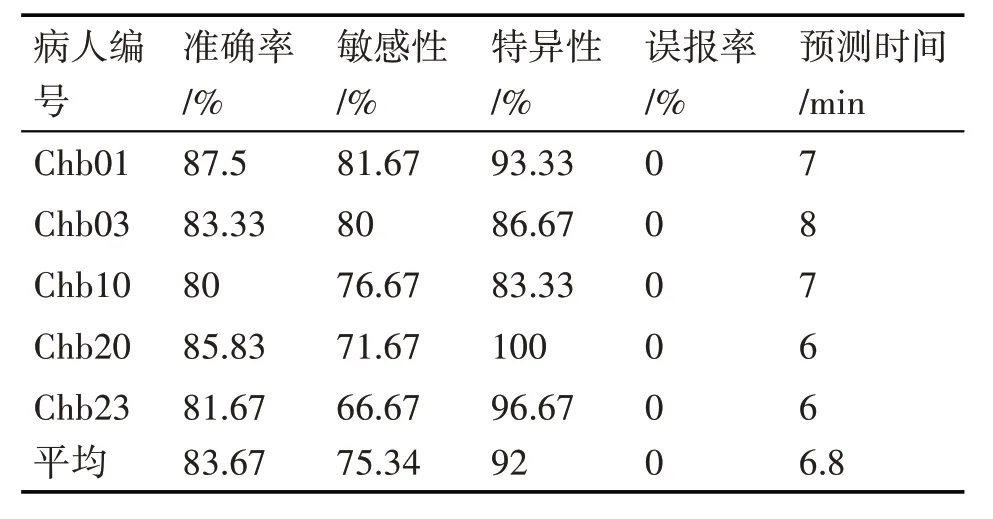
表3 五位癫痫病人预测结果

4 结语

癫痫发作前期与发作间期的脑电信号不同频段能量具有明显不同，采用小波包变换方法可以很好地提取出这一特征。同时经过粒子群算法优化后的支持向量机与随机参数方法、网格寻优方法相比，识别准确率更高、运行时间较短。此外，经实验验证了本文提出的阈值后处理方法在减少系统误报率方面的有效性。实验结果表明，本文方法准确率高，并且无误报率，预测时间也在合理范围内，为进一步研究实时性癫痫发作系统提供了参考价值。