喷嘴长度对射流式施肥器性能影响的数值研究*
俞晓峰,姚丽萍,2,陈涛,谢守勇,2,李光林,2
(1.西南大学工程技术学院,重庆市,400715;2.丘陵山区农业装备重庆市重点实验室,重庆市,400715)
0 引言
水肥一体化借助微灌技术,是一种节水节肥的精准化灌溉技术。其中,施肥装置及其性能是影响灌溉施肥质量的关键,目前,国内外常用的施肥装置有压差式施肥罐[1-2]、注肥泵[3-4]、文丘里式施肥器[5-9]以及射流式施肥器等。其中,射流式施肥器属于液液混合中心射流泵的小型化应用,主要利用从喷嘴喷出高速射流的卷吸作用在吸肥腔内部产生负压,进而将肥液从母液桶中吸出并与主管道水流混合,最终进入滴灌系统中送至作物根系。相较于其它传统施肥器,射流式吸肥性能好、工作范围广以及混合程度高;同时其在运行过程中振动与流量波动更小,从而使其在水肥混合调控中具有更高的稳定性。
射流式施肥器性能的主要影响因素包括吸肥腔结构参数、喉管长度、喷嘴结构以及空化特性等。相关学者现已开展了大量的研究工作。汪小珊等[10]对8种不同规格的射流式施肥器进行了性能测试,并推导了进出口压差与进口压力之间关系的公式,研究得到公式斜率主要受喉管截面和喷嘴出口截面的面积比的影响;袁寄望等[11]研究了吸肥腔收缩角、吸肥腔直径以及喉部直径比等结构参数对射流式施肥器吸肥性能的影响,并对这些结构参数进行组合优化设计;在液液混合中心射流泵的研究中,龙新平等[12]数值研究结果表明喉管长度与射流泵面积比有关,并确定了射流泵的最优喉管长度及其范围;袁丹青等[13]设计了一种多喷嘴射流泵,可以通过缩短主管水流和被吸流体混合均匀长度来减小喉管长度。周良富等[14]利用理论与数值计算相结合的方法研究射流式混药装置结构参数对其性能影响,结果发现面积比以及喷嘴出口与混合式吸入口之间的距离对性能影响最大,并通过分析获得参数最佳取值范围。在射流泵空化特性研究方面,Liu等[15]在对大面积比的中心射流泵的数值模拟中观察到空化气泡均是从吸入腔与喉管相接处产生并向下游延伸,随着时间演化呈现周期性波动;Xu等[16]通过实验验证了由速度梯度引起的压力脉动可以作为预测空化的判据;Wang等[17]通过实验研究了射流泵在不同喉管长度、喉管类型以及扩散角下的空化特性,结果表喉管结构对空化强度有显著影响。当射流式施肥器进出口压差增大到一定数值之后(正常工况外)会发生剧烈的空化现象,从而限制吸肥能力进一步提升[10]。现有的报道中关于射流式施肥器的研究集中于正常工况下吸肥腔结构对吸肥性能的影响。射流式施肥器中吸肥腔是水肥混合的核心部位,而其内部结构尤其是喷嘴长度(不同的喷嘴长度对应不同的喷嘴结构),是影响吸肥其性能的关键因素。然而,目前不同喷嘴长度射流式施肥器的空化特性对吸肥性能影响方面的研究鲜有报道,亟需进一步研究。
基于此,本文提出采用计算流体力学手段对不同喷嘴长度的射流式施肥器吸肥性能进行研究,并对其影响机制进行调查分析,以强化施肥器的吸肥性能。首先研究了施肥器在不同进出口压差下吸肥量的变化规律;然后,调查了喷嘴长度对吸肥量、吸肥浓度、进口流量比和吸肥效率等性能指标的影响规律;最后,通过对施肥器内部流场分析,揭示了不同喷嘴长度空化特性对吸肥性能影响的机制。
1 问题描述和数值公式
1.1 物理模型
本文所采用射流式施肥器结构模型如图1(a)所示,主要包括收缩段、吸肥腔、吸肥管、喉管、扩散段和出口五个部分组成。工作时,主管道水流由进口流入,经收缩段后流速变大形成高速射流,在吸肥腔经卷吸作用形成负压,将肥液由吸肥口吸入管道,并与水在喉管中混合后由扩散段流出进入管路中。建立主管道的水流方向为x轴方向,肥料进入吸肥管道的方向为y轴方向,z轴方向符合右手螺旋定则。相应的截面示意图如图1(b)所示,射流式施肥器总长为150 mm,其他主要结构参数进口直径D1、出口直径D2、吸肥口直径DT、收缩段角度α、扩散段角度β、喷嘴口直径d1以及喉管直径d2,主要结构尺寸见表1。

表1 射流式施肥器关键结构尺寸参数及特征表Tab.1 Key structural and dimensional parameters and characteristics of jet fertilizer injector

(a) 结构模型
在施肥器吸肥腔结构中,有一根正好贯穿吸肥腔并与吸肥腔圆柱长度L一致的管道[10],即为喷嘴,其长度始于与收缩段连接处,止于喷嘴出口。
1.2 基本控制方程
本文假设射流式吸肥器内部为不可压缩流体,且不考虑温度场的变化,湍流模型采用标准k-ε模型进行数值模拟,其中湍动能系数k及湍动能耗散率ε的运输方程如式(1)~式(4)所示。
(1)
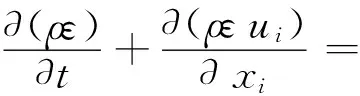
(ε/k)(Cε1P+ρCε2ε)
(2)
(3)
μt=Cμρ(k2/ε)
(4)
式中:ρ——流体密度;
μ——动力黏度系数;
ui——速度分量;
k——湍动能系数;
ε——湍动能耗散率;
t——时间;
μt——湍流黏度;
δk——湍动能k对应的普朗特数;
δε——湍动能耗散率ε所对应的普朗特数;
P——湍动能生成项。
经验常数Cε1=1.44,Cε2=1.92,Cμ=0.09,δk=1.0,δε=1.3。
空化流动的数值模拟基于均相流模型,采用ZGB质量运输空化模型,其中气相质量运输方程如式(5)所示。
(5)
式中:αn——气相体积分数;


(6)
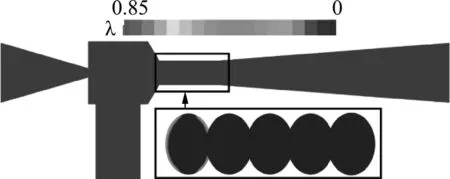
p (7) 式中:Fvap、Fcond——蒸发系数和凝结系数,Fvap=50,Fcond=0.01; αnuc——单位液体所含气体的体积分数,αnuc=5×10-4; p——饱和蒸汽压; psat——水压; R——气泡半径,R=1×10-6。 在施肥器边界条件的设置中,p1、p2、p3分别为施肥器进口压力、出口压力以及吸肥口压力值。进口和吸肥口边界条件均设置为压力入口,考虑到施肥器离肥料液面有一定距离,故吸肥口压力p3设置为-5 000 Pa;本研究基于自循环式实验装置[11],对应仿真模型出口边界为自由出流状态,因此出口为压力出口,p2数值为0 MPa;施肥器管壁粗糙度设置为0.03 mm。 为验证程序有效性,本文对文献[18]中对称W1型文丘里施肥器模型(出口压力p2保持0.1 MPa不变,进口压力设置为0.18~0.30 MPa,增量为0.01 MPa)吸肥量的数值计算进行重复,本文所得计算结果(图2)与文献的计算结果相比最大相对误差为6.46%,误差在可接受范围之内,表明数值模拟方法的可靠性。 图2 程序有效性验证Fig.2 Program validation 本文采用结构化六面体网格对计算流域进行离散,并对吸肥腔与喉管处进行加密处理。为保证计算结果准确可靠,进行了网格无关性验证。选择四种网格数量:0.9×105、1.1×105、1.3×105、1.5×105,对同一问题(入口:0.6 MPa、出口:0 MPa、吸肥口:-5 000 Pa)进行对比计算,计算所得吸肥量与网格量的关系如图3所示,综合考虑计算的准确性以及计算量的大小,最终采用1.5×105的网格进行相应的数值计算。 图3 网格无关性验证Fig.3 Grid-independent verification 为强化射流式施肥器的吸肥性能,本文基于文献[10]中射流式施肥器模型,研究了不同喷嘴长度对施肥器性能的影响。喷嘴长度分别选取L、3L/4、L/2、L/4以及0的5种情况。图4(a)、图4(b)和图4(c)分别对应喷嘴长度为0、L/2和L时的施肥器结构,以及局部放大的三维喷嘴结构。相应的结构尺寸见表2。 表2 喷嘴结构尺寸Tab.2 Nozzle structure size (a) 喷嘴长度0 射流式施肥器的基本性能指标包括有吸肥量q、吸肥浓度θ、进口流量比M和吸肥效率η,计算如式(8)~式(10)所示。 (8) (9) (10) 式中:Q——进口流量,m3/h。 本文首先研究了进出口压差ΔP对吸肥量的影响规律,计算中施肥器出口压力保持为0 MPa,进口压力设置范围为0.1~1.0 MPa(增量为0.1 MPa)。图5是喷嘴长度为L时射流式施肥器吸肥量与进出口压差的关系曲线图。从图5中可以看出,随着进出口压差的不断增大,施肥器的吸肥流量表现为先快速增加后趋于平缓的趋势。在进出口压差为0.1~0.5 MPa范围内,施肥器的吸肥量随着进出口压差的增大近似于线性增长;当进出口压差为0.5 MPa时,吸肥量出现拐点,随着进出口压差的继续增大,喷嘴长度为L的射流式施肥器吸肥量基本保持在1.49 m3/h不再明显增加;这表明在进出口压差达到0.5 MPa之后施肥器内部水力损失增大,导致吸肥量无法进一步提升。本文数值计算结果与文献[10]中射流式施肥器的吸肥规律一致,说明了本文所使用数值模型的可靠性。 图5 进出口压差对吸肥量q的影响关系曲线图Fig.5 Influence of differential inlet and outlet pressure on the amount of fertilizer absorbed 为强化施肥器吸肥性能,本文对比研究了不同进出口压差条件下(0.6~1.0 MPa),五种不同喷嘴长度对施肥器性能的影响,相应的影响关系曲线如图6所示。 (a) 吸肥量 图6(a)为不同进出口压差下喷嘴长度对吸肥量的影响曲线。可以看出,喷嘴长度不变的条件下,随着进出口压差的增加施肥器的吸肥量均有所增大,其中喷嘴长度为L时,吸肥量增长较小。而不同进出口压差条件下,随着喷嘴长度的增加,施肥器吸肥量近似单调递减,喷嘴长度为L时吸肥量达到最低。进出口压差数值反映了主管流道在施肥器工作过程中的压力损失,当进出口压差为1.0 MPa时,定量分析得到喷嘴长度为0、L/4、L/2和3L/4相对于喷嘴长度L的吸肥量分别提高了21.01%、20.14%、17.67%以及11.67%。研究结果表明,在相同的压力损失条件下,喷嘴长度较小的施肥器的内部压能相较于长喷嘴的施肥器能更好地转化成肥液动能。 图6(b)和图6(c)分别为喷嘴长度对施肥器吸肥浓度和进口流量比的影响曲线。可以看出,进出口压差逐渐增加时,不同喷嘴长度条件下的施肥器吸肥浓度和进口流量比均呈递减变化;而进出口压差不变的条件下,随着喷嘴长度的增加,射流式施肥器的吸肥浓度和进口流量比的变化趋势相似,均为先增大后趋于下降,并在喷嘴长度为L/2和3L/4之间存在峰值,而在喷嘴长度为L时为最小。图6(d)表明喷嘴长度对吸肥效率的影响相对较小。由其计算公式可知,吸肥效率与进口流量比成正相关,因此喷嘴长度对吸肥效率的影响曲线与其对进口流量比的影响曲线的特征相似;在相同进出口压差条件下,随着喷嘴长度的增加,吸肥效率总体先缓慢增加后下降。 综上所述,吸肥腔内部的喷嘴长度会对施肥器的吸肥性能产生显著影响。喷嘴长度过长会影响射流式施肥器的吸肥性能,不同进出口压差下,喷嘴长度为L施肥器在吸肥浓度、进口流量比和吸肥效率几方面的性能指标均为最低;且当进出口压差为1.0 MPa时,较小喷嘴施肥器的吸肥量均比喷嘴长度为L的吸肥量多10%以上。 本文进一步对施肥器内部流场进行分析,以揭示喷嘴长度对施肥器性能影响的机制。基于以上研究结果,本文对进出口压差为0.6 MPa时,喷嘴长度为0、L/2和L的施肥器内部流场特性进行对比分析。 图7为喷嘴长度为0、L/2和L的射流式施肥器z=0截面上的静压分布图。从图7(b)中可以看出,喷嘴长度为L/2条件下的吸肥腔内部的负压分布区域面积最大(图中箭头所示位置,即吸肥管道与喉管入口相交处),喷嘴长度为0条件下的负压分布区域面积次之(图7(a)),而喷嘴长度为L时的负压分布面积最小(图7(c))。射流式施肥器中,吸肥腔负压区域的压能可转化为肥液动能,负压分布的大小决定了吸肥能力的大小;而喷嘴长度为L时吸肥腔内负压面积最小,这是其吸肥量较低的一个主要原因。 (a) 喷嘴长度0 通过对图7中喉管和扩散段的观察发现,三种施肥器的负压区域(压力数值接近或达到饱和蒸气压)均从喉管入口处开始沿着流道向下延伸;相比之下,喷嘴长度为L时的负压区域延伸范围最广,直至扩散段前端。在施肥器中,当局部压力低于饱和蒸气压时,水体中相应区域因空化而不断产生空泡,空泡数量的增加则会影响施肥器的内部流态,进而影响其吸肥性能。这是喷嘴长度为L的施肥器吸肥性能较低的另一个因素。 为明确空化现象对吸肥量的影响,本文对喷嘴长度为0、L/2和L的射流式施肥器内部的空化现象进行了分析。图8描述了施肥器内不同喉管位置处(即x=5 mm、10 mm、15 mm、20 mm、25 mm截面)的气相体积分数分布情况。气相体积分数是气相在气液混合物中所占的体积分数,可反映候管部空化的分布情况。气相体积分数数值越大则意味着在该区域的空化强度越大。 (a) 喷嘴长度0 从图8(a)和图8(b)可以看出,喷嘴长度为0和喷嘴长度为L/2时,施肥器空化区域仅存在于喉管开始位置,且为环状空泡薄膜。而喷嘴长度为L的施肥器内的环状空化不仅在喉管开始位置出现,而且紧贴着喉管壁面形成环状空化并沿主流向下延伸,且向下游不断增厚直至扩散段前端,如图8(c)所示。根据文献[15]报道,射流泵中空泡群受到回射流影响在扩散段中脱落,会堵塞整个流道,制约被吸流体流量。研究结果表明,喷嘴长度为L时,吸肥器内空化程度最为剧烈,气液两相之间的能量交换越频繁,其会制约吸肥量的增加,因此,相应的吸肥性能指标最低。 通过对射流器内部流场分析可知,不同喷嘴条件下,施肥器内部的负压分布,相应的空化现象及其占比,是影响射流式吸肥器吸肥性能的主要原因。 1) 射流式施肥器吸肥量随着进出口压差的增大而增大,当压差到达一定数值后,吸肥量不再明显增加;喷嘴长度为L的施肥器进出口压差的拐点为0.5 MPa。 2) 喷嘴长度对射流式施肥器的吸肥性能有显著影响。进出口压差为0.6~1.0 MPa条件下,喷嘴长度为L的施肥器的吸肥浓度、进口流量比和吸肥效率几个方面性能指标均最低;且当进出口压差为1.0 MPa时,相较于喷嘴长度为L的条件,其他较小喷嘴长度的施肥器的吸肥量均提高10%以上。 3) 通过对射流器内部流场分析可知,不同喷嘴条件下,施肥器内部的负压分布,相应的空化现象及其占比,是影响射流式吸肥器吸肥性能的主要原因。本研究可为射流式施肥器的设计提供相应的理论支撑。2 程序和网格有效性验证
2.1 程序有效性验证
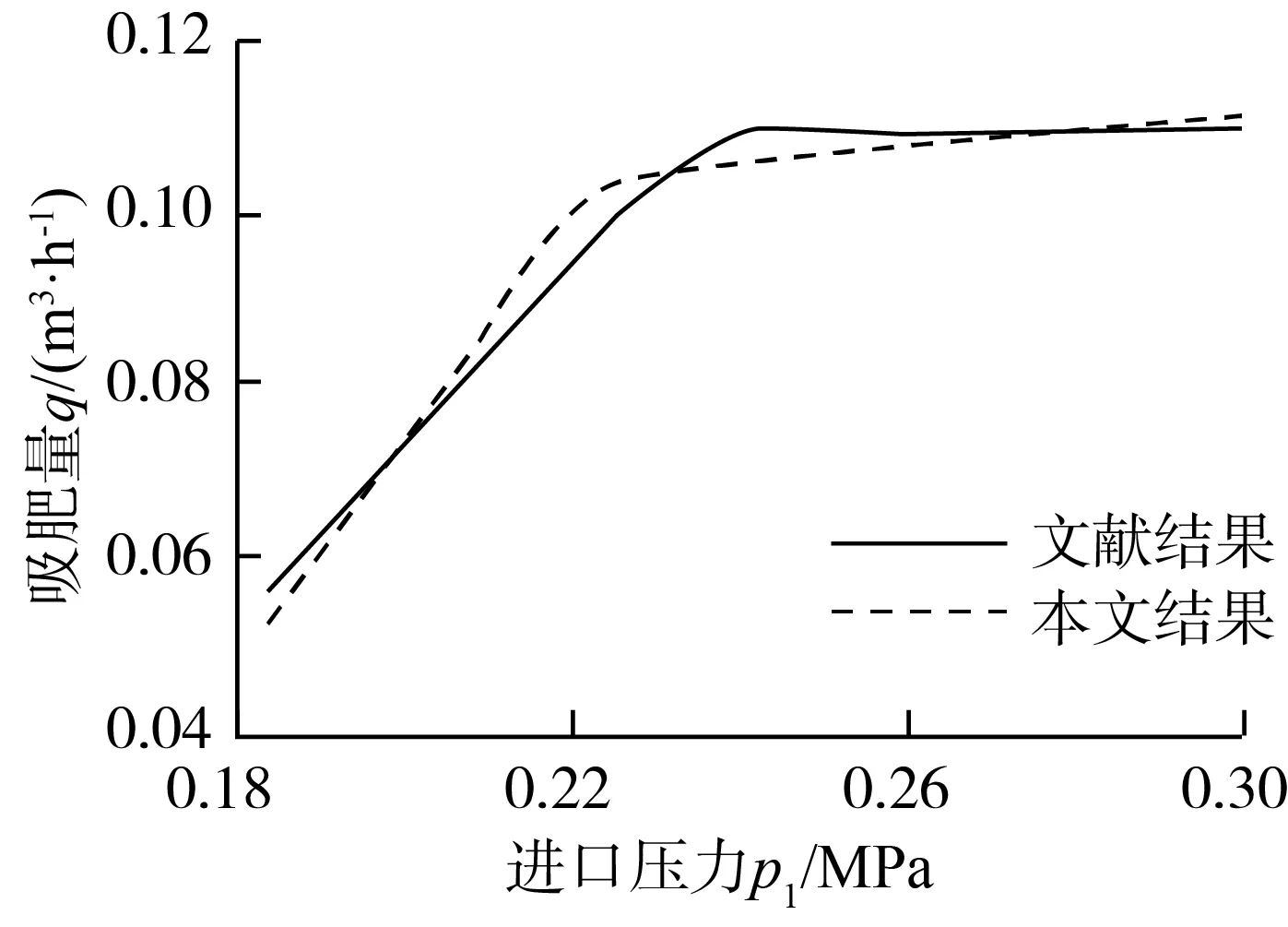
2.2 模型有效性验证
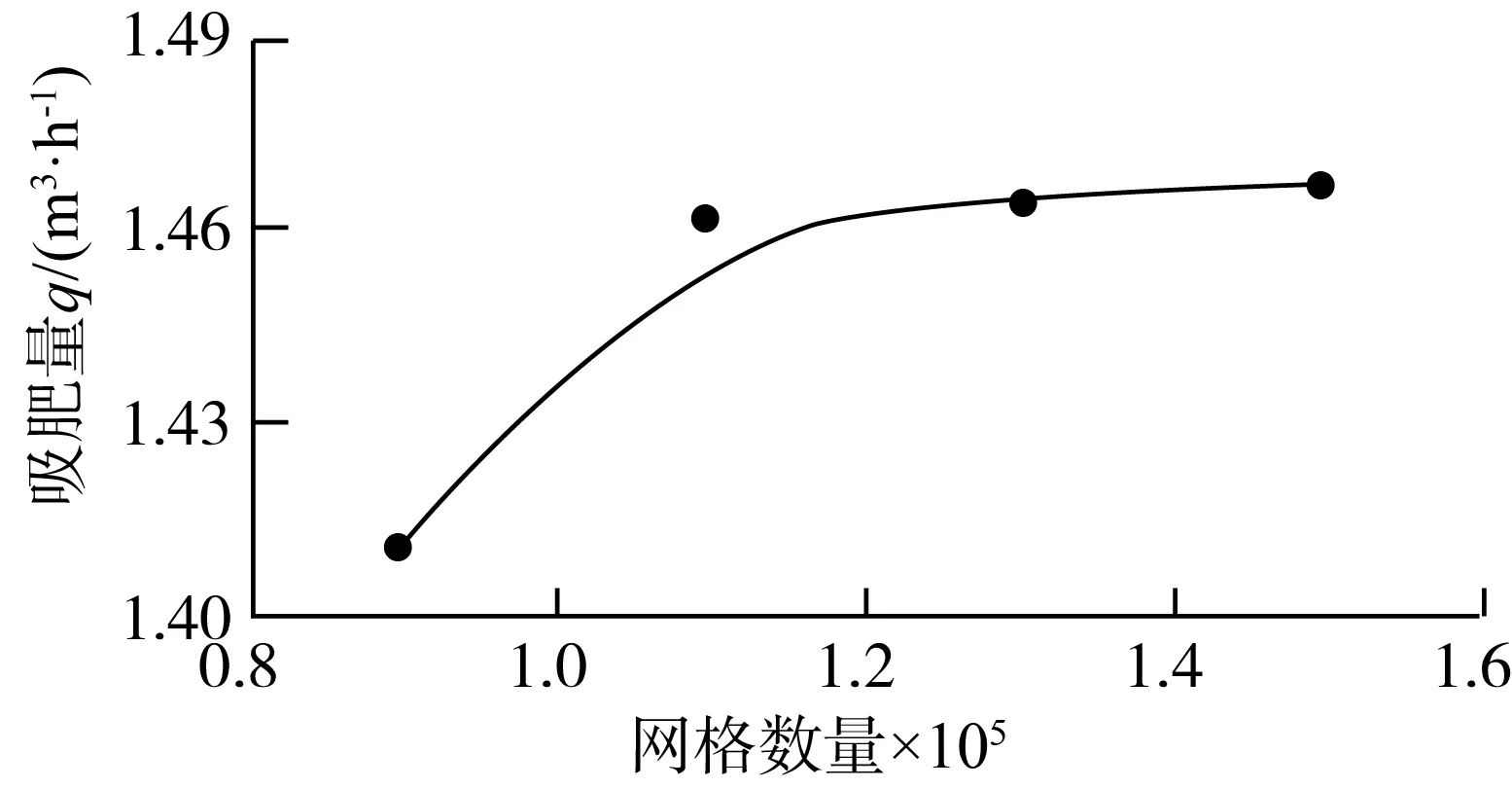
3 结果与分析
3.1 结构及几何参数


3.2 进出口压差对吸肥量影响规律研究

3.3 喷嘴长度对吸肥性能影响规律研究

3.4 施肥器内部流场分析
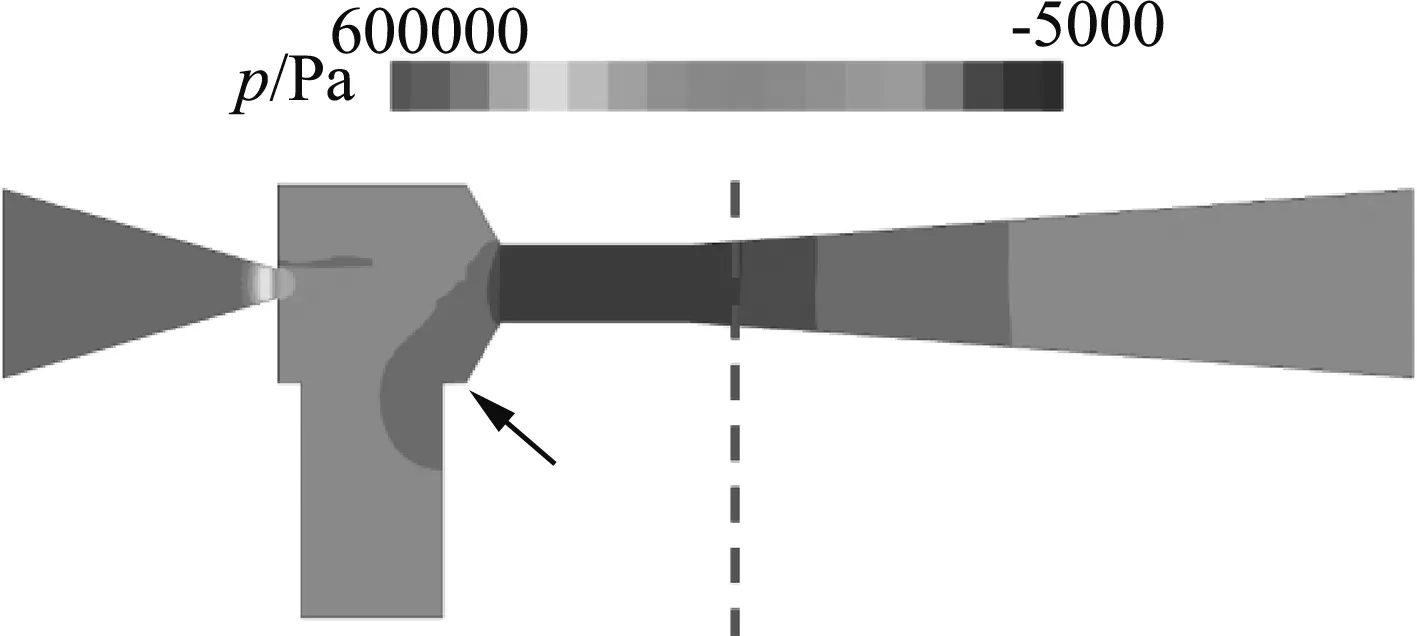
4 结论
——以首场广东喉管·唢呐独奏音乐会为例

