非保形平流层飞艇升空过程热力耦合建模与压差控制分析*

侯凯振,杨朝旭,荣海军,靳鹏飞

1.西安交通大学机械结构强度与振动国家重点实验室,西安 710049 2.西安交通大学陕西省先进飞行器服役环境与控制重点实验室,西安 710049 3.西安交通大学航天航空学院,西安 710049

0 引言

平流层飞艇具有载荷量大、驻空时间长、覆盖范围广、制造费用相对较低等优点,具有重要的军事及民用价值,可广泛应用于战场侦察、区域预警、环境监测、通信中继、区域导航和应急救灾等领域。由于其所具有的经济性、空间性、通讯性和前景性,越来越得到各国的重视[1-4]。现有平流层飞艇大多借鉴放飞高空气球的方式,不完全充气释放,而让其在上升过程中逐渐膨胀成型,如SWRI、Aero-star公司和AFRL对HiSentinel-20的试飞[5]、HiSentinel-80的试飞[6]。采用这种放飞方式的飞艇被称为非保形平流层飞艇。飞艇的气囊体积变化与压强变化对其安全运行起着决定性因素,日本SPF平流层飞艇计划中的GPS-1号模型就是因为飞艇不能及时排放气体导致内部压强过大最后在高空破裂[7]。因此,研究非保形平流层飞艇在升空过程中气囊体积和压强的变化,以及构建内外压差调节机制对保障飞艇正常安全飞行有着重要意义。

平流层飞艇在升空过程中,周围环境的压强、温度、密度、太阳辐射、红外辐射、热交换等均会对飞艇内部的温度、压强产生影响,因此存在复杂的热力耦合问题[8-9]。为了对飞艇的飞行状态进行深入研究,多名学者建立了热力耦合模型。Harada等[10]建立了平流层飞艇的热力学理论模型,并通过一系列小型飞行器的飞行试验,验证了模型的有效性;Shi等[11]建立了平流层飞艇热力学模型,获得了平流层飞艇在上升和下降过程中的温度变化;姚伟等[12]建立了平流层飞艇上升过程的热力学模型,并在此基础上对飞艇的上升过程仿真分析得到艇内外压差、上升速度,以及外界大气的对流换热、太阳热辐射等因素对飞艇净静升力的影响。然而现有的这些模型仅仅着重研究了平流层飞艇升空过程的热效应,而没有考虑升空过程中气囊体积变化和压强变化。

平流层飞艇的升空过程中内外压强会随着温度和大气密度的变化而变化,但飞艇的安全飞行需要压差保持在一定的范围,既要保证囊皮结构安全还要维持飞艇构型,因此控制飞艇内外压差至关重要[13-14]。Zhu等[15]结合模糊推理的方法,通过改变排气阀门面积实现飞艇压差控制,该方法采用一系列模糊if-then规则建立飞行状态与排气阀门之间的关系,获取特定飞行状态下的压差控制。该方法需要根据设计者的经验为模糊控制器创建模糊推理规则,当飞行状态改变时,需要人为地根据经验改变规则库,缺乏实时在线学习能力。然而动态飞行环境导致飞艇的飞行状态时刻发生变化,因此设计一种能够适应动态环境下的压差控制器是十分必要的。

本文以非保形平流层飞艇为研究对象,建立非保形平流层飞艇热力耦合模型,得到飞艇上升过程中气囊体积、压强差等变化规律。针对平流层飞艇上升过程中外部环境复杂,飞艇内部压强难以实时准确获取的问题,提出基于模糊观测器的压差控制方法,所提方法利用模糊系统实时获取压强的观测值,为了保证实时学习能力,利用在线顺序模糊极限学习机(OS-Fuzzy-ELM)去训练模糊系统参数,克服传统模糊推理系统依赖经验不能在线学习的缺点。通过改变阀门面积对飞艇内部压强和大气压强之间的压强差进行控制,结果表明,压差可以很好地跟踪设定值。

1 热力耦合建模与压差控制仿真框架

为了开展升空过程非保形平流层飞艇气囊体积变化及压差控制的研究,以飞艇是否成形的标准将非保形平流层飞艇升空阶段分为自由膨胀上升阶段和成形上升阶段。当氦气囊和空气囊的体积之和为飞艇的总体积时,自由膨胀上升阶段结束,进入成形上升阶段;成形上升阶段中飞艇总体积保持不变。如图1所示,分别建立自由膨胀上升阶段和成形上升阶段的热力学模型,并与动力学模型进行耦合形成平流层飞艇升空过程热力耦合模型;设计基于OS-Fuzzy-ELM的模糊观测器实现飞艇内部压强的实时观测,并将压强的状态观测值用于PID控制器的误差输入计算中,实现基于模糊观测器的平流层飞艇压差控制。

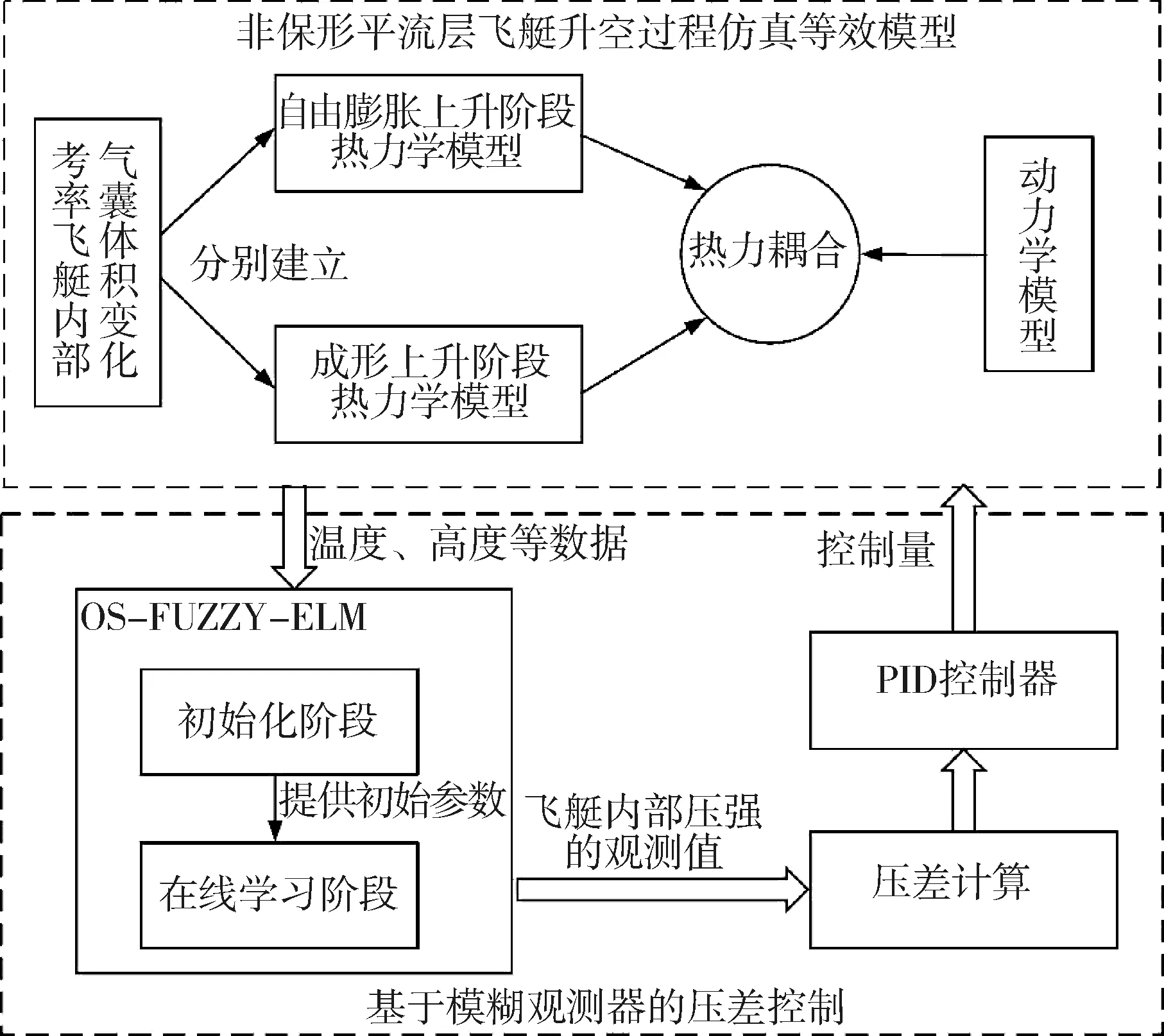
图1 热力耦合建模与压差控制仿真框架

2 非保形平流层飞艇升空过程热力耦合建模

2.1 非保形平流层飞艇热力学建模

在非保形平流层飞艇的上升过程中,将空气囊中的空气和氦气囊中的氦气假设为理想气体,满足以下的理想气体状态方程:

PheVhe=nheRThe

(1)

PairVair=nairRTair

(2)

其中:Phe和Pair分别代表氦气和空气的压强,Vhe和Vair分别代表氦气和空气的体积,nhe和nair分别代表氦气和空气的物质的量,R为摩尔气体常数,The和Tair分别代表氦气和空气的温度。

2.1.1 自由膨胀上升阶段的热力学模型

Phe=Pair=Ph

(3)

(4)

其中:Ph代表大气压强。

对式(1)～(2)两边分别求导可得:

(5)

(6)

(7)

(8)

当Vhe+Vair=V时,即氦气囊和空气囊的体积之和为飞艇预设的总体积V时,自由膨胀上升阶段结束。

2.1.2 成形上升阶段的热力学模型

在成形上升阶段中,飞艇总体积V不发生变化。空气囊和氦气囊的压强相等,满足以下关系:

Phe=Pair

(9)

(10)

此阶段中氦气继续膨胀,体积增加;空气囊体积减小,空气通过阀门排出。但二者之和仍为飞艇的总体积,满足以下关系:

Vhe+Vair=V

(11)

(12)

此阶段中当空气囊即飞艇内部的压强大于外界大气压时,即Phe=Pair>Ph时,空气囊开启阀门排放空气。此时涉及到空气质量的改变,由于nair=Mair/μ,其中Mair为空气的质量,μ为空气的摩尔质量,式(2)变为:

(13)

对式(13)两边分别求导可得:

(14)

结合式(9)～(12),对式(5)和(14)进行联立化简得到:

(15)

(16)

(17)

其中:nr为排气阀个数,S为单个排气阀面积,C为排气常数,ρ1为气体密度,ΔP=Pair-Ph为空气囊压强与外界大气压强的差值。

2.2 平流层飞艇热效应

平流层飞艇的升空过程的热效应影响包括外部影响和内部影响。外部影响包括蒙皮的红外辐射以及与外部环境的对流换热等因素;内部因素包括表面与内部气体之间的对流换热等因素[13]。因此描述飞艇热效应的影响需要对大气环境进行建模,并计算飞艇内部的热量变化,从而得到飞艇温度变化情况。

2.2.1 大气环境模型

平流层飞艇上升过程是从地面放飞至平流层的过程。环境温度Th,大气压强Ph和密度ρh均会发生变化,变化方程如下[16]:

(18)

(19)

(20)

其中:T0=288.15 K,ρ0=1.225 kg/m3,P0=101325 Pa。

2.2.2 飞艇热量计算

本文主要考虑平流层飞艇不同气囊之间以及飞艇与大气层之间的对流换热,不考虑太阳辐射的影响。假设平流层飞艇在上升过程中符合热平衡上升过程,即气囊气体与外界大气有较强烈的传热过程,气囊内氦气和空气与外界大气保持热平衡[12]。飞艇热量计算由以下5部分组成:

1)蒙皮的红外辐射

飞艇内部气囊和外部蒙皮温度均高于绝对零度,均会发出红外辐射,而来自内部的辐射部分被蒙皮吸收。蒙皮的红外辐射qir,f可表示为:

(21)

其中:波尔兹曼常数σ=1.3806505×10-23J/K,ε为蒙皮的红外发射率,αir为蒙皮对红外辐射的吸收率,Asurf为飞艇的表面积,Tf为飞艇蒙皮的温度。

2)蒙皮与大气层的对流换热

蒙皮与大气层对流换热的热量qf,a可表示为:

qf,a=Hf,aAsurf(Tf-Th)

(22)

其中:Hf,a为蒙皮与大气层的对流换热系数。

3)蒙皮与氦气囊的对流换热

蒙皮与氦气囊对流换热的热量qf,he可表示为:

(23)

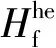
4)蒙皮与空气囊的对流换热

蒙皮与空气囊对流换热的热量qf,air可表示为:

(24)

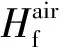
5)氦气囊和空气囊的对流换热

氦气囊与空气囊对流换热的热量qair,he可表示为:

qair,he=KAair,he(Tair-The)

(25)

其中:K为隔膜的导热系数,Aair,he为氦气囊和空气囊接触面积。

2.2.3 飞艇的温度计算

在完成飞艇内部热量建模后,通过热力学定律对飞艇气囊温度和蒙皮温度进行计算。根据热力学第一定律,空气囊和氦气囊的能量方程表示为:

(26)

(27)

其中:Mhe和Mair分别为氦气和空气的质量,Che和Cair分别为氦气和空气的比热容,Qhe和Qair分别为氦气和空气的热量,计算方程为:

Qhe=qf,he+qair,he

(28)

Qair=qf,air-qair,he

(29)

飞艇蒙皮的能量方程为:

(30)

其中:mf为飞艇蒙皮的质量,Cf为蒙皮的比热容,Qf为蒙皮与外界的能量交换,计算方程为:

Qf=-qir,f-qf,a-qf,he-qf,air

(31)

在飞艇热效应的计算过程中,式(18)～(20)中大气温度Th、大气密度ρh和大气压强Ph均与高度h有关,因此需要建立动力学模型来研究飞艇的运动状态;同时由于热力学模型中求解得到的飞艇的氦气体积Vhe和空气体积Vair直接决定飞艇的浮力,因此在模型迭代求解的过程中需要将热力学模型和动力学模型进行耦合。

2.3 非保形平流层飞艇动力学建模与热力耦合

2.3.1 平流层飞艇动力学建模

平流层飞艇需依靠气囊提供的浮力实现升空和悬停。根据动量定理,升空过程中飞艇的运动方程为:

(32)

其中:M为飞艇的总质量,由氦气质量Mhe,空气质量Mair和载重Mp构成,M=Mair+Mhe+Mp。g为所在高度的重力加速度。

式(32)中,Ff为飞艇所受的浮力

Ff=ρhg(Vhe+Vair)

(33)

Fz为飞艇所受阻力

(34)

其中:CD为阻力系数,v为飞艇相对大气运动的速度。

在自由膨胀上升阶段中,由于飞艇自由膨胀,因此飞艇质量不变,式(32)变为:

(35)

在成形上升阶段中,随着飞艇排放空气,式(32)变为:

(36)

2.3.2 热力耦合过程

以上的建模过程表明平流层飞艇升空过程中存在复杂的热力耦合问题,而对热力耦合精确建模是实现实时状态控制的关键[8]。本文所提的热力耦合建模充分考虑了实际飞艇飞行过程中体积与压强的变化,符合实际飞艇的飞行特性,为飞艇的实时控制提供了良好的基础。具体的热力耦合实现过程如下:结合当前时刻的大气温度、大气密度、大气压强与氦气囊、空气囊和蒙皮的温度,通过飞艇热量计算与温度计算得到氦气囊、空气囊和蒙皮的温度变化率。迭代计算下一时刻的氦气囊、空气囊和蒙皮温度,并计算当前时刻的飞艇压强和气体体积的变化率。迭代计算下一时刻的飞艇压强和气体体积。根据当前时刻的飞艇压强和气体体积结合大气环境模型计算动力学模型中的浮力阻力等物理量,得到当前时刻飞艇的速度变化率,通过迭代计算得到下一时刻飞艇的高度。至此完成模型的一次迭代计算。

从成形上升阶段热力学模型式(15)中可以看出飞艇在成形上升阶段的内部压强与空气囊空气的排放有关,因此可以通过控制空气排放调节飞艇内部压强,从而实现对飞艇的压差控制。

3 基于模糊观测器的平流层飞艇压差控制

飞艇是充气的柔性体,必须通过压差控制将飞行过程中的内外压差保持在安全范围内[17]。在平流层飞艇升空过程中,受低温、气囊体积变化等因素的影响,飞艇内部压强无法准确测量。因此本文使用模糊系统对飞艇内部压强进行在线观测从而获得实时压强信息。为了确保模糊系统的实时学习能力以适应飞行过程中的不确定变化,利用在线顺序模糊极限学习机(OS-Fuzzy-ELM)对模糊系统参数进行在线更新。

OS-Fuzzy-ELM是由Rong等[18]提出,它可以以逐个或逐块模式顺序学习数据,学习复杂度低并成功应用于非线性系统识别与控制问题[19-20]。因此,为了使平流层飞艇内外压差保持在安全范围内,本文根据OS-Fuzzy-ELM算法设计基于模糊观测器的PID控制器对飞艇进行压差控制。

3.1 基于OS-Fuzzy-ELM的模糊观测器

模糊系统通常包括两大类型,即Mamdani类型的模糊系统和Takagi-Sugeno-Kang(TSK)类型的模糊系统。由于TSK模糊系统的规则后件是关于输入的线性表达式,具有系统复杂度低的优点,因此利用TSK模糊系统设计压强观测器。TSK模糊系统由以下一系列规则构成:

Rulei: if (x1isA1i) AND (x2isA2i) AND…AND (xnisAni), thenyisβi

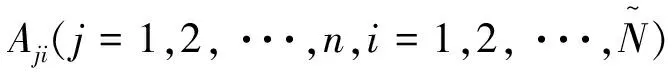
本文采用5层结构的TSK模糊系统结构,如图2所示。输入层的每个节点代表一个输入变量,并将输入信号直接传输到模糊化层。模糊化层的每个节点表示每个输入变量的隶属度值,其值由隶属度函数μAji决定,任意一个有界非恒定分段连续函数g均可以作为隶属函数,例如高斯函数、三角函数等。本文采用高斯函数作为隶属度函数,

μAji(xj;cji,ai)=g(xj;cji,ai)

(37)

其中:cji和ai对应于第i条模糊规则下第j个输入变量xj的隶属度函数g中的参数。模糊推理层的每个节点表示通过模糊逻辑AND运算获得的if-then规则的if部分,它可以是任何类型的T范数。第i条模糊规则的激活强度为:

Ri(x;ci,ai)=μA1i(x1;c1i,ai)⊗μA2i(x2;c2i,ai)⊗
…⊗μAni(xn;cni,ai)

(38)

图2 模糊系统结构

其中:⊗表示任何类型的T范数运算,本文采用的是product范数。正则化层的节点被命名为正则化节点,其数量等于模糊推理层中的节点数量。第i个正则化节点表示为:

(39)

其中:G为模糊基函数。输出层的每个节点对应于一个输出变量。系统输出通过每个正则化规则的输出的加权和来实现。

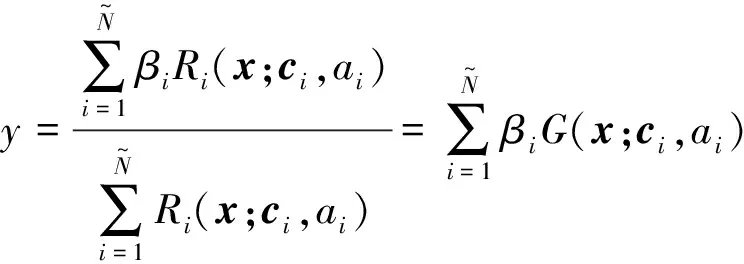
(40)

式(40)进而可写成以下的矩阵形式:

y=QTH

(41)

其中:H为隐藏矩阵,Q为模糊模型的参数矩阵,分别为:

(42)

(43)

为了实现模糊系统的在线学习能力,需要对模糊系统中的参数(c,a,Q)进行学习。不同于传统的梯度下降法,OS-Fuzzy-ELM不需要对隶属度函数参数(c,a)进行迭代优化。在OS-Fuzzy-ELM算法中,参数(c,a)仅仅需要随机赋值,不需要任何先验信息,后件规则参数(Q)就能够线性解析地进行求解,从而获得高速精确的运算。

本文通过TSK模糊系统实现对飞艇内部压强的状态观测,将与飞艇内部压强P相关的物理量—氦气温度The、飞艇高度h、阀门面积S、飞艇内部空气密度ρ1、前一时刻飞艇内外压差ΔP和氦气体积Vhe作为模糊系统的输入变量x;将模糊系统的输出值y设定为飞艇内部压强P的状态观测量。结合OS-Fuzzy-ELM算法[15],本文模糊观测器的观测过程分为初始化和在线学习2个阶段,如图3所示,具体学习过程如下:

1)初始化阶段

选取飞艇成形上升阶段中的少量数据作为训练样本,进行OS-Fuzzy-ELM的初始化学习。在这个阶段中,完成隐含层神经元个数的确定,并随机生成模糊隶属度参数c和a,生成初始矩阵H0和初始参数矩阵Q0,为在线学习提供参数。

2)在线学习阶段

利用飞艇成形上升阶段的实时数据更新系统,结合初始化阶段得到的参数完成系统输出矩阵H和输出权值Q的计算。在此基础上得到输出值,即为飞艇内部压强P的状态观测量。

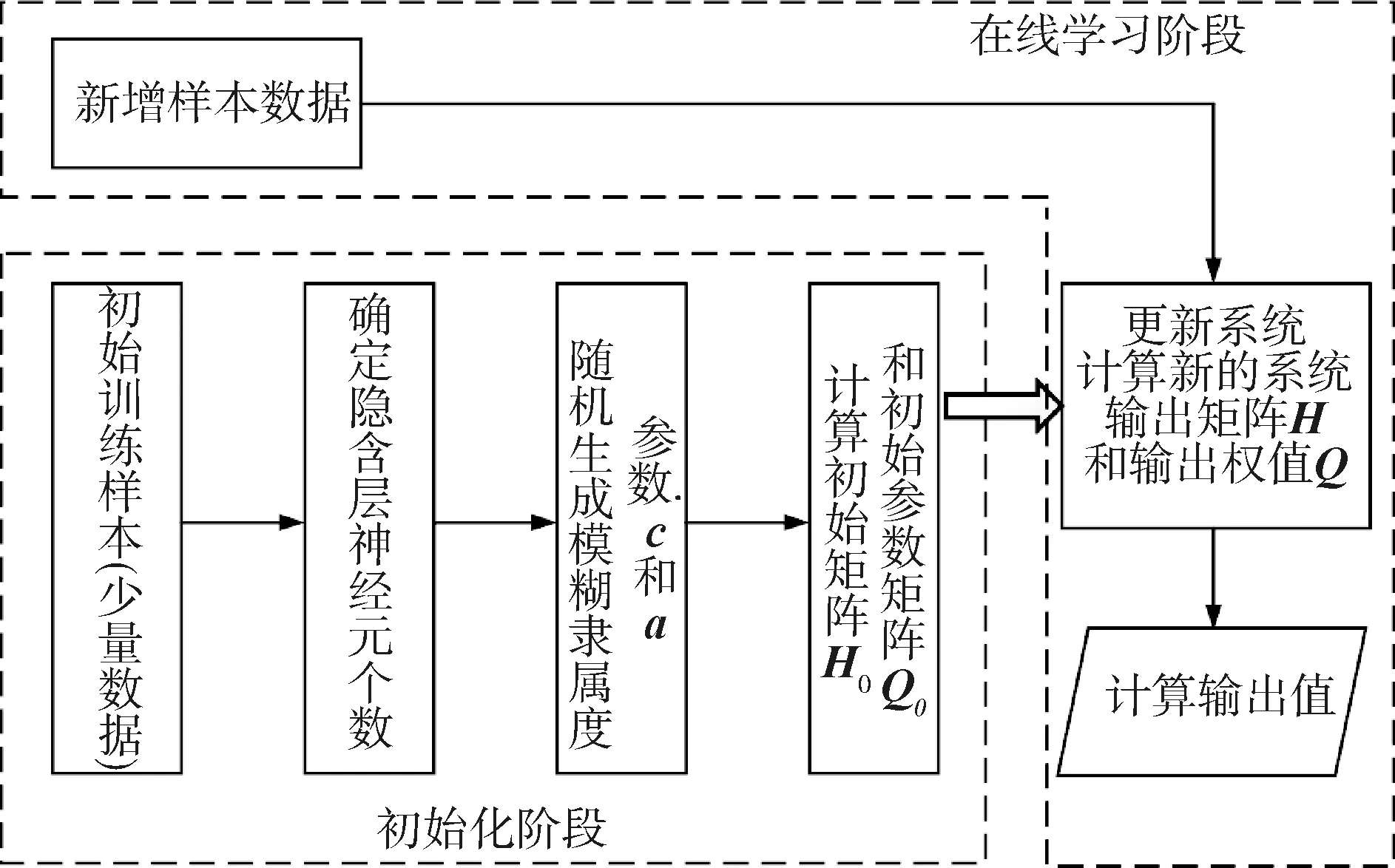
图3 基于OS-FUZZY-ELM的模糊观测器学习预测流程

3.2 基于模糊观测器的平流层飞艇压差PID控制器设计

飞艇在成形上升阶段中需要控制空气的排放,使得飞艇的内外压强差稳定在一定的安全范围内。结合飞艇排气方程式(17)可知,飞艇的阀门面积S与飞艇的空气排放量直接相关,因此通过改变阀门面积可以调节飞艇的内部压强P,从而使飞艇内外压差符合安全范围。因此本文采取的控制量为飞艇阀门面积S,并假设飞艇的阀门可以按照任意闭合度进行调节。由于飞艇阀门存在最大面积,因此控制量存在最大上限,本文中模拟飞艇阀门的最大面积是0.5 m2。

如图4所示,根据实时监测的飞艇状态数据,利用OS-Fuzzy-ELM算法观测飞艇内部压强P,获得飞艇内部与外部环境的压强差ΔP′,结合基于OS-Fuzzy-ELM的模糊观测器构建PID控制器,降低飞艇实际压强差ΔP与预定目标压强差ΔPd之间的误差,实现飞艇实际压强差对目标压强差的跟踪。

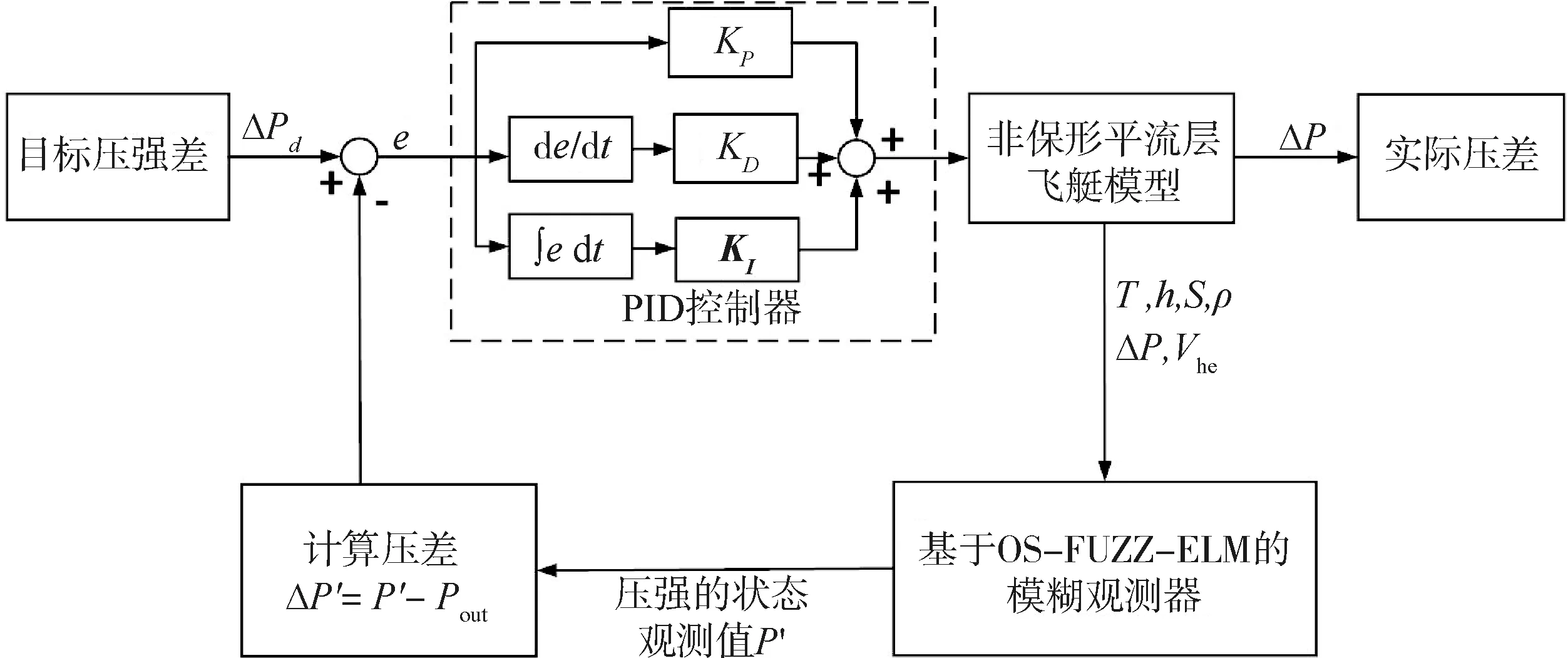
图4 基于模糊观测器的平流层飞艇压差PID控制器框图

4 仿真分析

根据非保形平流层飞艇升空热力耦合模型,采用MATLAB仿真软件,对非保形平流层飞艇运动情形和压差控制进行仿真分析。模型采用欧拉法进行迭代,模型模拟总时长为2 h,迭代步长取0.2 s,迭代次数为36000。成形体积为30000 m3,充注氦气质量535.5 kg,体积为3000 m3;充注空气6125 kg,体积为5000 m3。飞艇净重(不包括气体重量)与携带载荷重量之和为500 kg。

4.1 平流层飞艇升空过程热力耦合模型仿真分析

当不考虑压差控制时非保形平流层飞艇的阀门有不开与全开2种状态,因此飞艇在升空过程中有两种极端情形:(Ⅰ)不开阀门情形。飞艇没有排放空气的能力,即飞艇在成形上升阶段的空气阀门的开放面积为0;(Ⅱ)全开阀门情形。飞艇的阀门一直全开,即飞艇在成形上升阶段的空气阀门固定为全部开放。以下对2种极端情形下飞艇的运动情况进行仿真分析。

1)不开阀门情形下飞艇运动仿真结果分析

地球上空9 ～10 km之间有一条较窄的高速气流带,集中在对流层上部或平流层中,具有强的水平切变和垂直切变,称为急流带[21]。飞艇上升速度需要大于3 m/s才可以穿越急流带到达平流层。如图5(a)所示,本文模拟的飞艇上升速度在穿越急流带时为5.0813 m/s,可以满足上述情况。在不开阀门情形对应的仿真结果中,如图5(b)所示,整个升空过程只存在自由膨胀上升阶段。在完成这一阶段后,氦气囊和空气囊之和达到了飞艇总体积,不再产生空气排放,因此飞艇完成自由膨胀上升阶段,再上升一定的距离后,就没有足够的升力再去上升,如图5(a)所示,飞艇在上升到12112 m之后飞艇在此阶段驻留。如图5(c)所示,在自由膨胀上升阶段,由于飞艇未成形,飞艇与大气压强的压强差为0。在完成自由膨胀上升阶段后飞艇还要上升一定的高度,期间外界大气压随着高度的上升而下降,而飞艇内部的压强没有变化,因此会产生较大的压强差,最高达到1882.9 Pa;此时压强差远大于飞艇的正常压差范围。

图5 不开阀门情形下的飞艇运动仿真结果

2) 全开阀门情形下飞艇运动仿真结果分析

如图6(b)所示,飞艇由自由膨胀上升阶段进入成形上升阶段。在成形上升阶段中,氦气继续膨胀,同时飞艇打开阀门开始排放空气;氦气囊的体积增大,空气囊的体积减小,但二者之和始终保持飞艇总体积,即该过程飞艇是成形的。如图6(a)所示,在完成自由膨胀上升阶段后,飞艇在成形上升阶段由于排放空气产生额外升力,飞艇继续上升一段距离,直至飞艇浮力与重力平衡达到上升的最大高度,之后在13628 m的高空驻留。如图6(c)所示,在进入成形上升阶段后,飞艇打开阀门排放空气。通过空气的排放,调节飞艇的内部压强使得飞艇与大气压强之间的压强差为0,此时飞艇上升到最大高度。由于对排气没有限制,这种情形的飞艇与大气压强之间的压强差最终为0,难以维持飞艇设计构型。

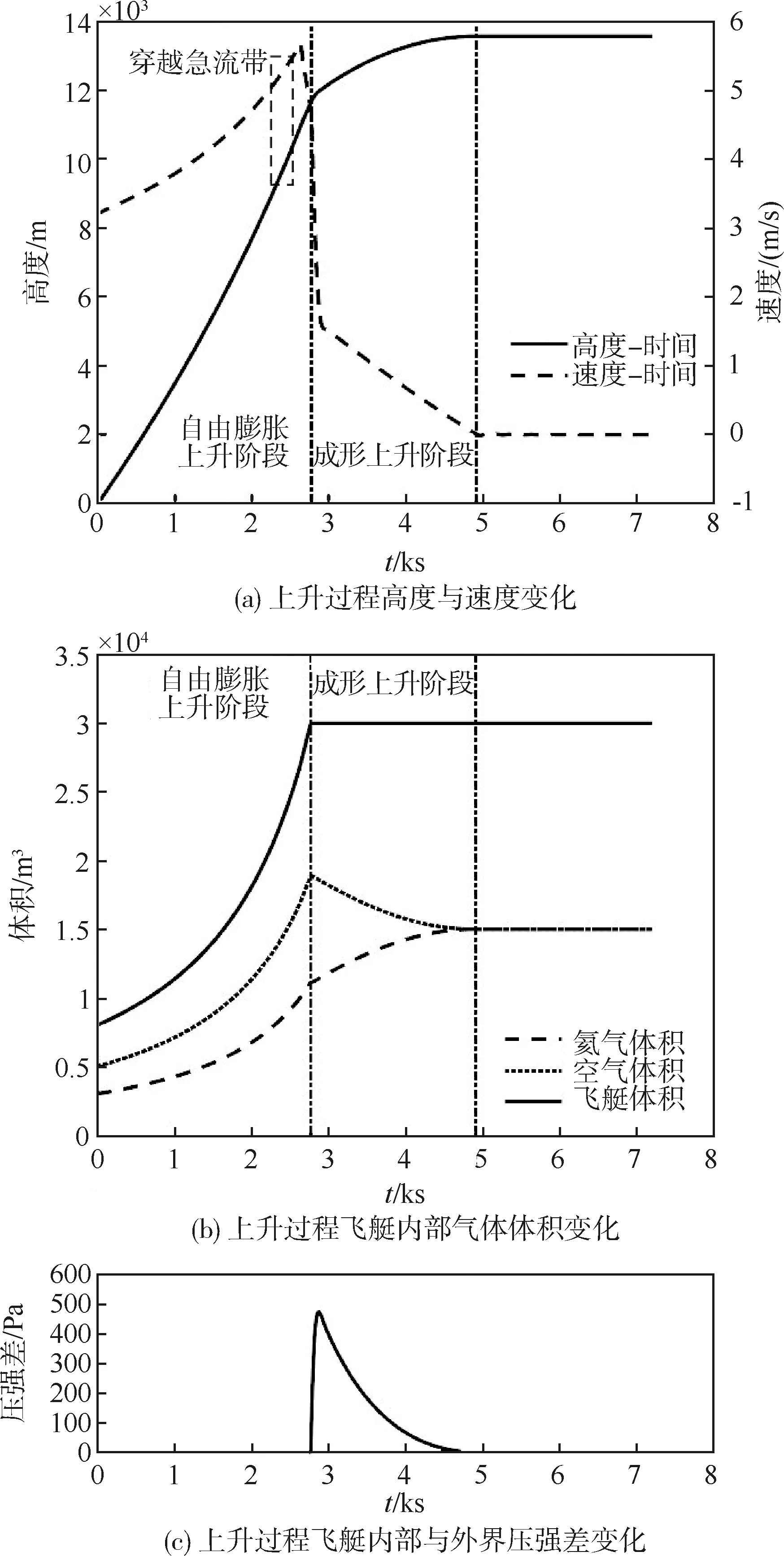
图6 全开阀门情形下的飞艇运动仿真结果

4.2 基于模糊观测器的平流层飞艇压差控制仿真分析

对比分析飞艇无压差控制的2种情形下压差的仿真结果可以得到:为了将飞艇与外界的压强差稳定在一定的安全范围内必须控制压差。在非保形平流层飞艇热力耦合模型的基础上添加基于模糊观测器的平流层飞艇压差PID控制器进行迭代求解,分析不同目标压强差下的压差控制结果。

取PID的3个参数分别为:KP=0.0025、KI=0.000001、KD=0.000005,目标压强差值分别为200 Pa、300 Pa和400 Pa,在MATLAB中进行仿真分析。

如图7所示,所设计的基于模糊观测器的平流层飞艇压差PID控制器可以实现对目标飞艇压强差的跟踪。当所追踪的目标压强差越大时,飞艇的阀门开放程度就越小,飞艇排放更少的空气就可以维持飞艇内部与外部的压强差。

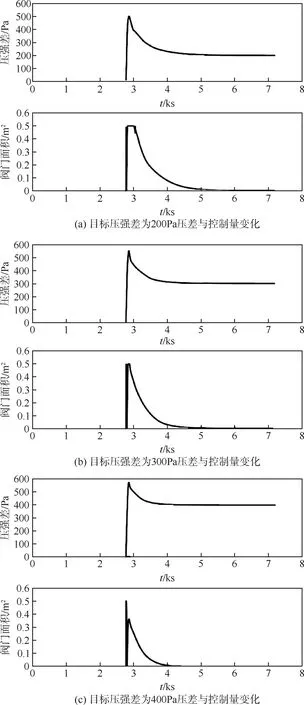
图7 不同目标压强差下的压差控制仿真结果(虚线代表期望值,实线代表实际值)

5 结论

以非保形平流层飞艇为研究对象,根据飞艇是否成形将其升空阶段分为自由膨胀上升阶段和成形上升阶段,分别建立对应的热力学模型与动力学模型进行耦合迭代求解。针对平流层飞艇升空过程中飞艇内部压强难以实时准确获取的问题,提出了基于模糊观测器的压差控制方法。所提方法利用模糊系统实时获取压强的观测值,利用在线顺序模糊极限学习机(OS-Fuzzy-ELM)去训练模糊系统参数,克服传统模糊推理系统依赖经验不能在线学习的缺点,保证了模糊观测器的在线学习能力;在此基础上构建了基于模糊观测器的PID控制器,通过改变阀门面积实现对飞艇内部与大气环境之间的压强差的有效控制。

通过对不开阀门与全开阀门两种情形下的非保形平流层飞艇热力耦合模型的仿真计算,获得两种情形下的压差结果与飞艇运动结果,对比结果验证了进行压差控制的必要性。仿真研究不同目标压强差下的压差控制,结果表明,所提出的基于模糊观测器的压差控制方法可以很好地跟踪目标设定值,该方法对平流层飞艇压差控制器的设计具有一定参考意义。