多平台声纳水下目标异步航迹序贯融合方法*

陈 洋 卢术平 丁 烽

（杭州应用声学研究所 杭州 310013）

1 引言

近几十年来，随着水声目标强度不断降低、海洋环境噪声不断加强，水声目标探测任务日益严峻，导致传统的探测手段的作用距离和作用效果不断下降［1］。为此，借助分布式融合技术来获取更好的探测性能，逐渐成为了研究的热门方向之一。

通常，为了更准确的目标状态估计，在分布式融合方法中需要满足各平台量测数据是同步一致的约束条件［2］。然而，由于分布式平台声纳的采样率、量测精度可能存在差异，并且还可能存在平台时/空配准问题、数据滞后或丢包等问题，令这个约束条件很难满足，导致传统的同步融合算法在实际应用中性能严重下降，甚至无法进行数据融合。

目前，主要将异步问题分为量测滞后、数据丢包、目标漏检等若干情况，并针对不同的异步问题采取相应的解决方法。对于量测滞后所导致的异步问题，Bar-Shalom等针对量测仅滞后一步和量测滞后多步的情况提出了解决方法。对于采样和传输速度不同导致的异步问题，许多学者也提出了一些解决方法，如分布式立方信息滤波、强无迹跟踪滤波器、转换测量卡尔曼滤波、粒子滤波、定时策略等方法［3～8］。此外，也有许多文献针对数据传输过程中数据丢包或传感器漏检所导致的异步问题进行研究［9～10］。

2 异步数据融合问题描述

异步融合问题的根本问题在于：由于我们通常使用离散时间系统模型来描述目标的连续运动过程，这就在多传感器数据融合算法的模型中，不仅要求了各传感器的观测过程是同步的，还要求了量测数据能够同步地到达融合中心［2］。

假设一个目标的状态方程可以描述为

其中，Ft+Δt|t为目标状态从t时刻到t+Δt时刻的状态转移矩阵，σt+Δt为噪声矩阵。

对于传统的多传感器融合算法而言，为了获取一个统计学上理论最优的融合估计结果，其融合算法大多数都约束每个传感器的数据是独立同分布的。但是，在实际应用中，由于每个传感器的时间戳均以各自平台为基准，以及声纳在传播过程中的声信道具有明显差异，导致各平台所描述的目标状态是存在明显差异的，即每个平台量测所得到的xt+Δt是有所不同的。当其中的时间差异Δt较小时，我们可以近似地得到一个较为准确的估计结果。但是，当多个传感器对该目标状态的量测差异较为明显时，即便不存在传感器的量测噪声，其融合结果也是不准确的，严重时可能还会影响算法的鲁棒性。因此，在实际应用中必须考虑如何解决传感器数据异步时的数据关联与融合问题。

如图1 所示，由于量测周期或者量测起始时间不同，导致传感器获取到不同时间的目标状态时，此时数据融合结果是不准确的。

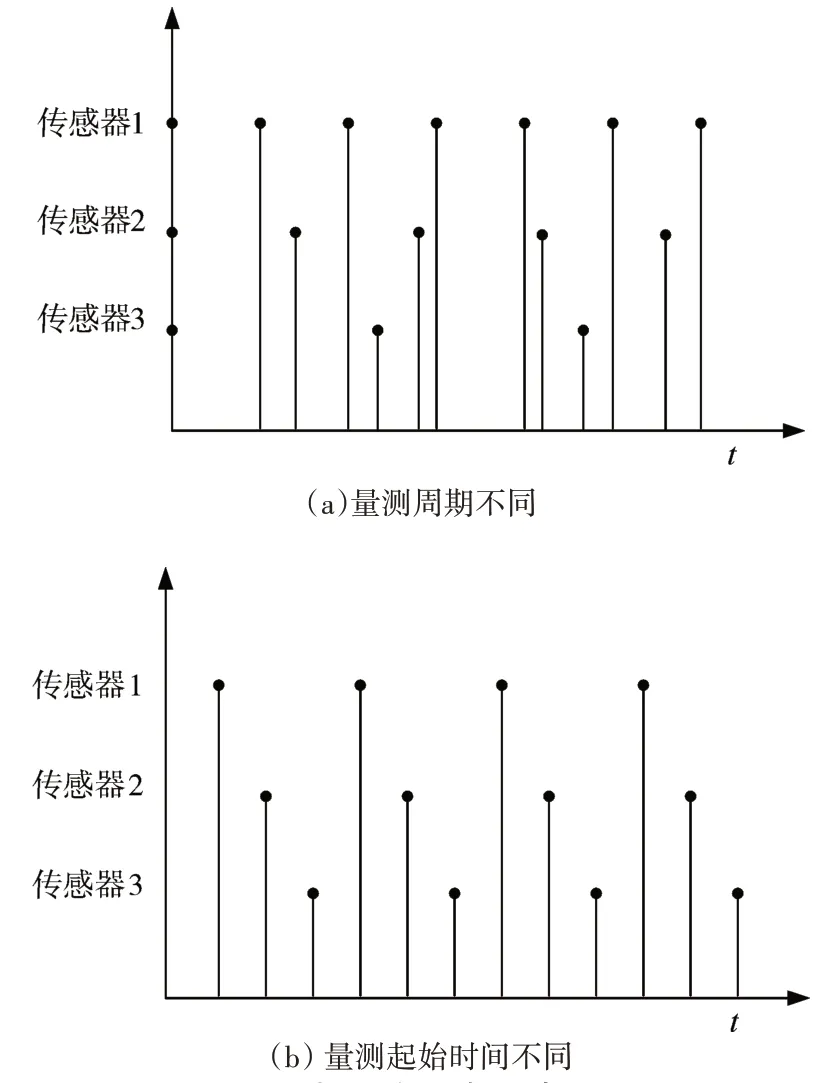
图1 常见的水声异步问题

3 基于分段关联门限的多平台异步序贯融合方法

目前常见的异步融合解决方案是序贯融合滤波思想［11］，因此本文在序贯融合方法框架下，针对由平台量测周期和起始时间不同导致的异步数据融合问题，提出了基于分段关联门限的多平台异步数据融合方法。

3.1 异步序贯融合框架

本文主要采用一种根据各平台量测顺序，依次计算相对时间差，并外推全局航迹，再将“伪同步”的全局航迹与局部平台航迹进行数据融合，完成对全局航迹更新的方法。

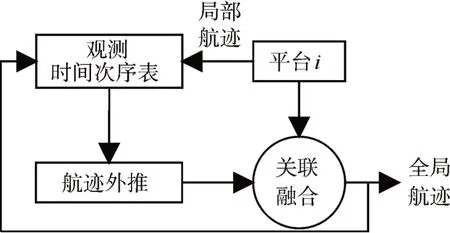
图2 异步融合示意图

通常，在水声目标跟踪探测领域中，常见的目标航迹状态向量X为目标的平面坐标及其速度，即

由于目标短时内可近为匀速直线运动，因此可以借助式（3），将t0时刻的全局航迹通过外推法得到tk时刻的全局航迹预测，来实现全局航迹和局部平台航迹状态在时间上的一致。

其中，外推时间Δt为

考虑到长时间不仅会导致航迹关联错误问题，而且还会大幅提高计算量，影响算法效率，因此本文仅对一定时间内的航迹进行外推，即将Δt＜MT内的航迹进行外推，其中MT为时间门限。

3.2 数据关联算法

对于多目标跟踪问题而言，数据关联问题通常是最优先需要解决的。在本文中主要采用最近邻域算法［12］对航迹进行关联聚类。

本文中，最近邻域算法的关联波门采用欧式距离。若两状态可以表示为[x1;y1] 和[x2;y2] ，那么这两个状态的欧式距离d为

推广至两平台多目标航迹关联时，则有：

那么，根据最近邻域关联算法理论，若两目标距离小于等于关联门限T，且满足为值是最小时，则可认为两个状态是最相关的。

由于本算法需要外推各局部平台的航迹，因此固定的门限T显然是不合适的。例如，由于模型的不准确、目标的航迹估计存在误差，导致外推时间长的航迹可能会存在较大误差，此时若采用较大门限，则会导致关联到错误航迹；若采用较小门限，则会导致无法正确关联目标航迹。因此，本文提出根据外推时间长短，采取一种分段式门限的最近邻域关联方法，即

其中，T1、T2……为距离门限。

3.3 数据融合算法

在实际应用中，由于多平台的局部航迹估计和全局航迹估计之间通常会存在未知大小的相关噪声，因此本文主要采用协方差交叉法（Covariance Intersection，CI）［13］进行数据融合。

对于双平台而言，该方法可以通过式（9）和式（10）实现：

其中，ω∈[0，1]为的最优权重，P为协方差矩阵，a，b表示两平台局部航迹估计，c表示融合航迹估计。

将上述公式推广到多平台融合时，则有：

3.4 滤波算法

由于水下弱目标探测环境的复杂性，局部平台跟踪结果中仍然可能存在许多干扰目标航迹，因此本文提出一种利用目标全局航迹的点迹个数、存活时间和目标运动状态进行滤波的方法，即目标特征函数滤波方法。

对于一个全局航迹而言，首先统计该航迹的量测次数，若量测次数少于NT次，则该航迹很可能是个假航迹，即使是目标的航迹，其量测数据较少，也可能会导致后面统计评估方法不准。其次计算该航迹的存活时间Δs=t1-t0。这里，t1为该航迹最新一次更新时间，t0为第一次检测到该航迹的时间。

最后，计算该目标的运动速度均值vmean=mean([v1，v2，…])，这里mean(·)为均值函数。若Δs≤ST且vmean∈[vmin，vmax]，则输出该航迹，否则继续观察。这里ST为存活时间门限，vmin和vmax分别为检测目标速度的下限和上限。

4 实验数据分析

本文借助了仿真和2017 年、2021 年两次试验数据进行实际数据验证分析。

4.1 仿真分析

在[-5000，5000] ×[-5000，5000] （m2）的范围内，共模拟3 个目标航迹100 帧数据，其中目标1 和目标2 都从第1 帧起出现，目标3 为在第60 帧时的新生目标，3 个目标均在第100 帧时消亡。目标1从位置(-500，2500 )以10节的速度向315°（以X轴正向为起点逆时针计算）方向行驶；目标2 从位置(-2000，1500 )处以6 节的速度向0°方向行驶；目标3则以4节的速度向225°方向行驶。

各平台的检测概率pD=0.6，平台的量测噪声的标准差为25m。平台1 的量测周期为30s，平台2的量测周期为40s，且相对平台1 滞后9s。此外，异步融合算法的参数T=300(m) ，MT=3(min) ，Δs=5(min)，NT=10(个)。那么，两平台的跟踪结果和本算法的处理结果如图3所示。

图3 仿真处理结果

可以看出，由于两平台的采样率不同，探测起始时间不同，导致各平台探测目标数据量和时间是存在差异的，如图1 的目标航迹数据量明显多于平台2。但是，经过本算法融合后，可以正确地形成三个目标的航迹，可见本算法可以有效地解决异步数据融合问题。

4.2 实验分析

采用2017 年中国某水域的一次实验数据对本方法进行验证。在本次实验中，数据时长约30min，共有3 个探测平台，并且3 个平台的目标跟踪航迹结果如图4所示。

图4 三个平台的跟踪航迹

其中，算法相关参数设置为：T=1000(m)，MT=5(min)，Δs=5(min)，vmean∈[1，5](m/s)，NT=10(个) 。

异步融合结果如图5 所示。可以看出，相比任意单平台的跟踪结果而言，融合后的目标航迹相比任意单平台而言都更加完整、清晰，还滤除了较多干扰目标航迹，证明了本文的异步序贯融合方法和滤波方法在解决实际水声应用问题时的有效性。

图5 异步序贯融合航迹结果

本文还采用2021 年的一次约1h 的实验数据。在本次实验中共有两个探测平台和一个运动目标，运动态势如图6所示。

图6 海试试验态势图

由于本次水文条件相比2017 年更加恶劣，因此采用了本文的分段关联算法进行数据关联，其中MT=15(min)，Δs=5(min)，

本算法的处理结果如图7 所示。可以看出，对于同一个目标航迹而言，由于航迹外推时间存在差异，导致目标误差波门也存在差异，因此传统的固定关联门限方法得到了2 段航迹，而分段关联法不仅可以准确地形成1 段目标航迹，而且航迹更加准确，且航迹中错误的点迹较少。

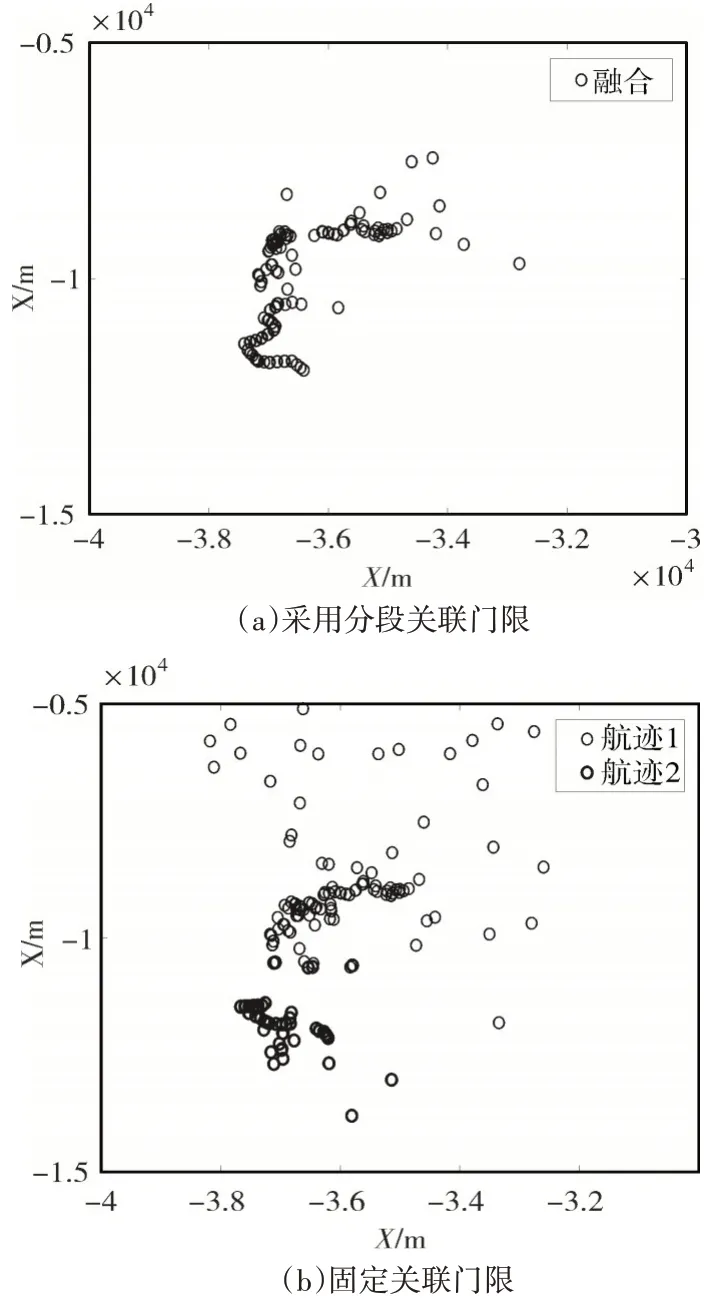
图7 异步融合目标航迹

5 结语

针对多平台协同探测过程中常见的异步问题，本文以序贯融合思想为基础，结合改进的数据关联算法、数据融合算法和滤波算法提出了一种新颖的多平台异步数据融合方法。仿真实验和两次实验数据处理结果表明本方法在一定条件下可以有效地滤除干扰信息，提高水声目标航迹估计的准确度，证明了本方法在解决实际问题中的有效性。