基于蜂窝模型中继台最小极值问题研究
岳梦楚,刘喜勋
(陕西工业职业技术学院 信息工程学院,陕西 咸阳 712000)
中继台(RP,repeater)是连接网络线路的一种装置,常用于2 个网络节点之间物理信号的双向转发工作[1]。主要是放大传输过程中衰减的信号,然后以不同的频率重新发送。中继台可使低功耗用户之间在互相不直接面对的情况下进行双向信息交流。诸多中继台参与信息传输会存在信号干扰,中继器[2]专线(Private Line,PL)可以帮助缓解此类困难。
在实际生活中使用中继台的情况复杂多变,需要考虑自然地理位置、天气、环境、人口数量等因素。为了降低成本,以最少的中继台数量完成用户信号传输,是人们在实际工作中亟待解决的问题。
研究者针对此类问题提出了很多方案,文献[3]分析了中继台的各种传播模型,并选择了Okumura-Hata模型[3],对典型场景下的中继台覆盖情况做了仿真预测分析。文献[4]为了达到最优化的通信开销,设计并实现了螺旋式网络中中继台的部署。Guan[5]提出使用BRSS 算法来选择中继台的最佳位置。Zhang 等人[6]则提出了一种近似算法,将中继台部署于联通情况下。Yang 等人[7]解决了如何在位置受限的情境下仍能高效部署中继台。以上算法皆着重于中继台位置的选择,而对中继台数量的选择并未进行研究。Cheng 等人[8]提出了单层无线网络中怎样放置中继台并使其数目最少的方法。Lin 等人[9]不仅使用最小生成树法实现了最小化部署中继台,且证明其是NP-hard问题。Chen等人[10]提出一个新的高效率模型——“三星结构”来达到最优化利用中继台。LOYD 等人[11]则针对双层网络情况提出了一种多项式时间近似算法解决中继台最少部署问题。
然而,以上研究均未考虑用户在线数量的情况。本文基于此,结合蜂窝模型、Egli公式以及地形校正因子,同时考虑用户不同时期数量变化,选取4 种情况进行研究。第一种是用户数量为1 000的情况,第二种是用户数量上升到10 000 的情况,第三种是地理位置从平原变化到山区的情况,最后一种情况是对模型的优化,即考虑人口分布不均匀的情况。
1 基本模型
1.1 中继台覆盖半径
为讨论方便,本节涉及的参数如表1所示。
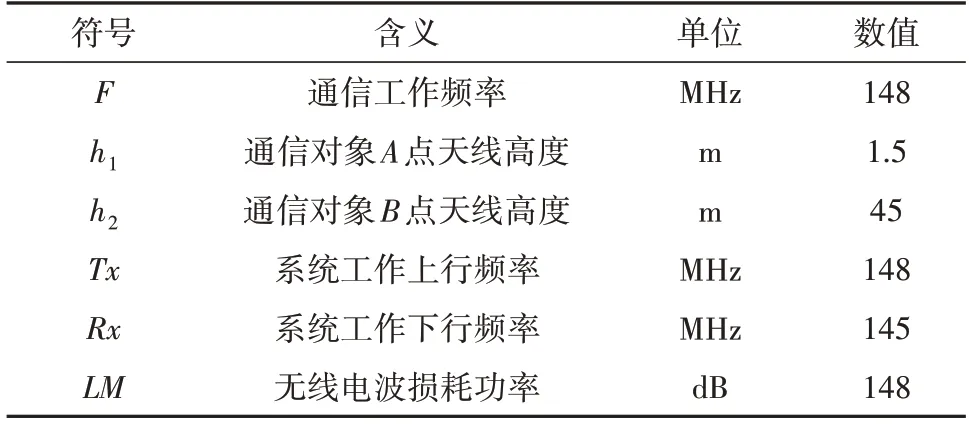
表1 传播损耗方程各参数说明Tab.1 The parameters of transmission loss
Egli模型[12]是计算无线电波传输损耗的实用工程公式,根据不规则多反射地形的大量测试结果发展起来的。该公式在平面大地模型基础上加入了各种修正因子。其基本传播损耗方程[13]如式(1)所示:
将表1 中各参数带入式(1)可得出上行信号覆盖距离dTx=15.2 km,下行信号覆盖距离dRx=69.5 km。
1.2 中继台能同时服务的最大用户量
设连续信道的带宽为B,输入信道的加性高斯白噪声n(t)的功率为N,信号s(t)的功率为S,则该信道的容量为
式(2)就是著名的香农(Shannon)信道容量公式,简称香农公式[14]。
香农公式表明,当信号与信道加性高斯白噪声的平均功率给定时,在具有一定频带宽度的信道上,理论上单位时间内可能传输信息量的极限数值。只要传输速率小于等于信道容量,总可以找到一种信道编码方式,实现无差错传输;若传输速率大于信道容量,则不可能实现无差错传输。
1.3 蜂窝模型
蜂窝通信[15]的概念是贝尔实验室研究人员在构造移动通信系统的无线电覆盖区时试图缓解频率拥挤问题而提出的。在全双工通信中,一个无线道包含了一对信道频率双向传输。由于电波传播损耗,一个频率在一个区域使用之后,干扰降低到可以接受的程度,于是这个频率就可以再用一次,这就是频率复用的概念。设置某个半径为R的地理区域C1内使用信道F1。这个信道F1在另一个相距D且半径为R的区域可以再次使用而不会产生较大的同频道干扰,如图1 所示。
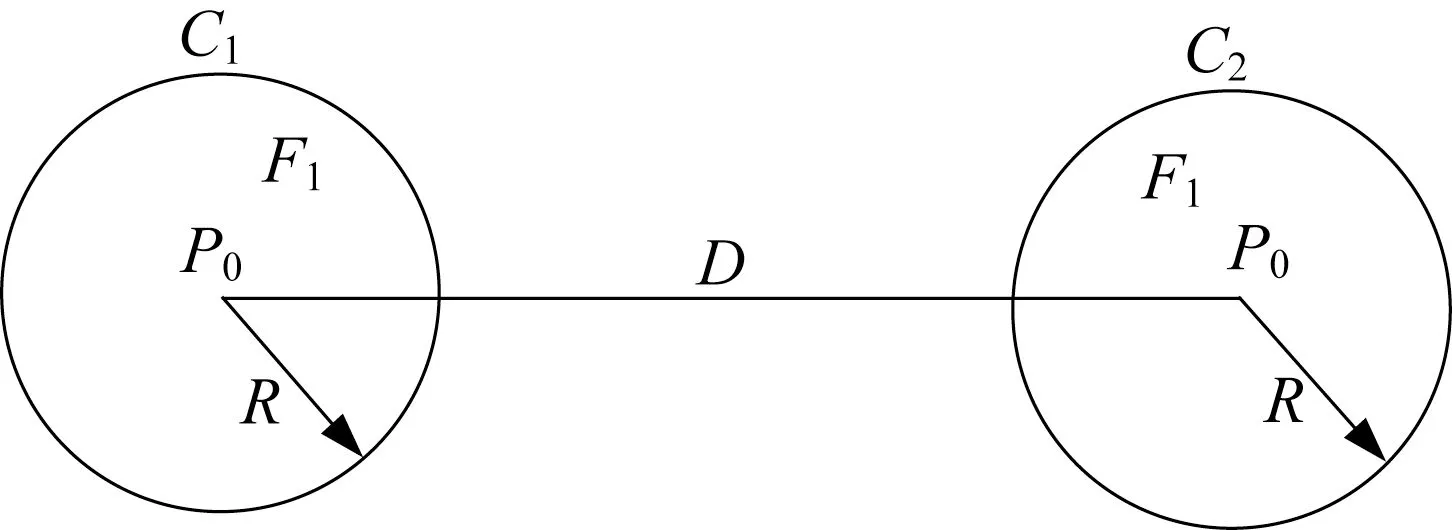
图1 蜂窝通信Fig.1 Cellular communication
图1说明多个相邻小区组成一个区群(cluster),同一个区群内各小区使用互不相同的信道频率,不同区群中相同编号的小区可以使用相同的信道频率,小区群中小区的个数即称为频率复用系数[16],也称作频率复用因子K。为了使一个或多个区群能无缝覆盖整个服务区域,且使小区尽量接近圆形,在蜂窝系统设计中往往采用六边形的小区。这种小区结构形如蜂窝,故称蜂窝小区(cell),如图2所示。
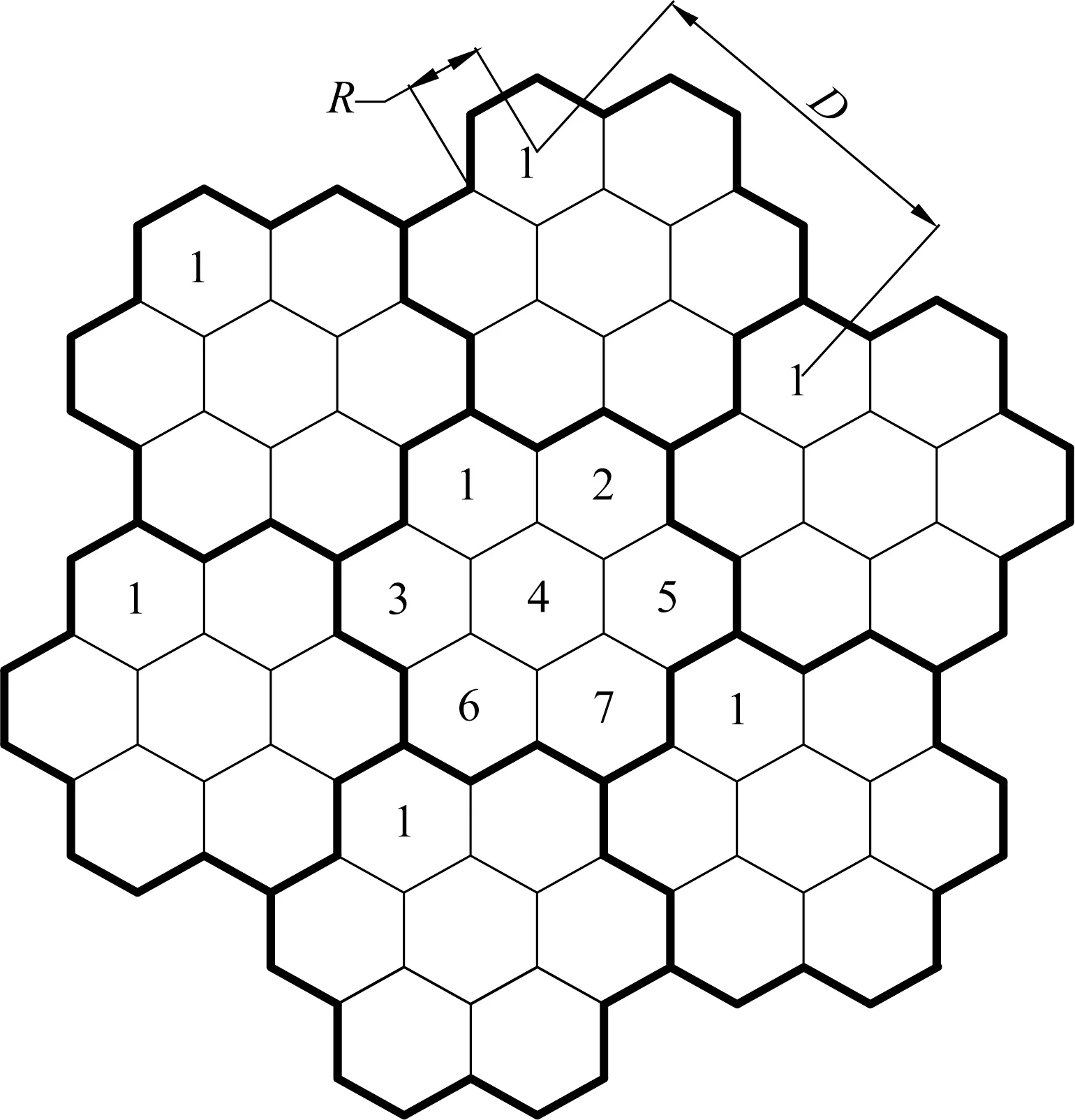
图2 蜂窝小区Fig2 The cell
频率复用因子K可由式(3)[17]计算得到,即
其中,D是同频复用距离;R是小区半径。
区群内的每个六边形小区都拥有一个中继台,每个中继台的信道都不同。通过充分分离的频率或者附带不同的中继器专线来设定不同的信道,从而使得相邻的中继台互不干扰。
参照有关通信组网方面的知识,一般用正多边形就可以无空隙、无重复地覆盖一个平面区域,可取的形状有正三角形、正方形和正六边形,其中正六边形更接近理想的圆形。结果证明,用蜂窝模型来完全覆盖某个平面范围所需点源的数目最少。
2 不同场景仿真
2.1 平原地形人数为1 000人
本文以覆盖范围R0为40英里的圆形区域为例,如图3 所示,不进行145~148 MHz 分频,仅使用中继器专线来区别不同的信道频率。区群内部的每个小区至少都安排一个不同的中继器专线,则蜂窝群里频率复用因子K就是中继器专线的个数。
由前述可知中继器覆盖范围等于上行覆盖距离dTx,最大客服量Np。用N0表示平原地形人数1 000,假设人口数均匀分布,则人口密度为
蜂窝群基圆半径即为小区半径R,则中继器覆盖范围内人数由式(5)得到,即
取蜂窝群基圆半径为中继器上行信号覆盖距离即R=dTx,将其代入式(5),得到Nd=33 本文采用离散数值方法[18]求解中继台极值问题。运用Matlab 7.0 编程计算可得出最少圆数约为30个,如图3 所示。对于本文,下行信号覆盖范围dRx就是同频复用距离D,而R=dTx,由式(3)可得K=7,即至少用7 个中继器专线才能满足在平原地形下用户数为1 000的通信需求。 此方法适用于任何半径情况。其优点是保证该区域内所有点都有中继站信号覆盖,其缺点是在区域边缘会有中继站覆盖面积的浪费。 仍旧假设人口均匀分布,由式(4)和式(5)可得基圆半径R=10.4 km,方法和前述一致,得到最少中继器数为59 个。同理由式(3)可得K=16,即需要的中继器专线数量至少为16个。 当地形是山区地形时,中继台的覆盖范围变小,此时重新计算d。在Egli 公式基础上引入地形校正因子CT,即 这里,CT=Ks+Kh+KA+Kis,参数说明见表2。 表2 修正因子参数Tab.2 The geography correction factor 本文考虑到山区的影响,只选用丘陵地形修正因子,则 对于山区地形,查找相关数据[19],当地形波动高度Δh=100 m 时对应取Kh=−5。在其他参数不变的情况下,根据式(7)算得d=11.4 km。 (1)当在线用户为1 000时,由式(4)和式(5)得出R=32.75 km >d,利用R=d的基圆去进行覆盖,方法和前述一致,得出最少中继台数为50。由式(3)得知,所需中继器专线数目为13。 (2)当在线用户为10 000时,同样得出R=10.4 km 整理上述仿真结果,如表3所示。 表3 不同场景计算结果Tab.3 The results of various senarios 由表3 可知,随着用户数量的增加以及地形从平原变换到山地时,中继器和中继器专线的数量也会随之增加。 该模型仅仅是针对人口均匀分布的情况,然而实际情况是各个区域的人口密度是有差别的。假设半径为R1的范围内人口密度为ρ,则圆面积为s的区域内的人数为 假设中继台i能同时服务的人数为ni,其覆盖半径为ri,覆盖面积si=,则有关系然后利用小圆面累加覆盖大圆面,即满足逻辑关系(s1∪s2…si…sn−1∪sn) ⊇s,s就是半径为R1的圆面积。 在满足这个逻辑关系的前提下中继台数最少,此时的模型适用性很强,只需知道范围内人口密度分布情况,就可求出满足所有用户同时在线情况的最少中继台数。 本文以在线用户量为1 000和10 000为例,基于蜂窝模型、Egli 公式以及离散数值方法计算每个中继台的覆盖半径,以此作为蜂窝通信模型基圆半径。在山区地形下,通过在Egli 公式中加入地形校正因子进行修正中继台的覆盖半径,并采用和平原地形同样的计算方法得出通信所需最少中继台数量。此外,当人口密度分布不均匀时,本文对上述模型进行了优化。实验结果表明,本文所提出的模型以及解决方案能够在各种约束条件下[20]以耗费最少代价实现最优目标。并且推断出本文所用方法在任意用户数量情况下均适用。2.2 平原地形人数增加到10 000人
2.3 山区地形

3 结果分析
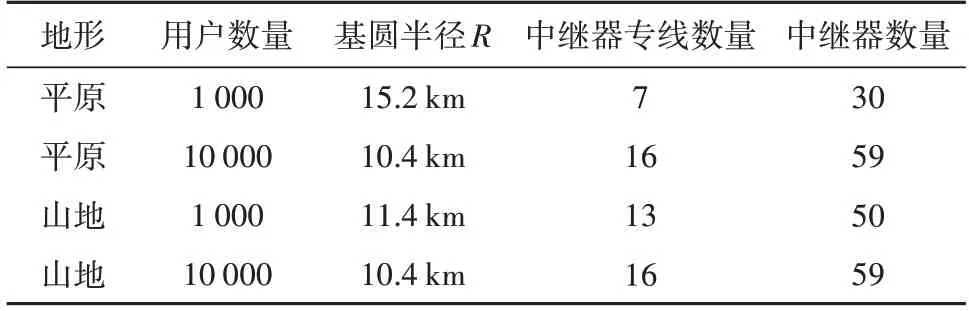
4 模型的优化
5 结论

