Adaptive allocation strategy for cooperatively jamming netted radar system based on improved cuckoo search algorithm

De-jiang Lu, Xing Wang, Xiao-tian Wu, You Chen

Aviation Engineering School, Air Force Engineering University, Xi'an, 710038, China

Keywords:Cuckoo search algorithm Netted radar system Radar countermeasures Resource allocation Information fusion

ABSTRACT

1. Introduction

With the continuous development of electronic information technology, the seizure of electromagnetic power has become the key to win the battlefield,among which radar countermeasure is an important link to win information warfare and electronic warfare.As the object of radar countermeasures,in recent years,the netted radar system [1—7] has received more and more attention from researchers. Compared with the traditional monostatic radar, the netted radar system consists of multiple radar nodes with different operating modes and locations, and by fusing the information collected by these radar nodes,the netted radar system can greatly improve the target search capability, tracking accuracy, airspace coverage and the anti-jamming capability.

Due to the information fusion advantages shown by the netted radar system,the aircraft formation is extremely vulnerable to the detection, tracking and positioning of the netted radar when performing assault missions in the absence of remote support,and the effectiveness of the traditional “one-to-one” jamming mode, in which one jammer interferes with one radar,is greatly reduced or even ineffective, which motivates us to study new cooperative jamming strategy.

In order to improve the jamming effect on the netted radar system and reduce the probability of the aircraft formation being detected and tracked by the networked radar, the use of multiplatform jammers in the air has become an important means of countering radar network technology. Under the constraint of limited jamming resources,jamming resources are supposed to be allocated scientifically and efficiently according to the tactical objectives,taking into account the number of radiation sources,threat level, signal parameters and other factors. Therefore, how to optimize the allocation of jamming resources has become an urgent problem to be solved.

Jamming resource allocation[8] requires to consider a series of issues such as“at what time,what jamming resource to choose,for what kind of target to interfere with, and how to evaluate the jamming effect.etc.”.The core of the problem is a multi-parameter and multi-constrained nonconvex NP-Hard problem, currently,some progress has been made in the study of the jamming resource allocation problem.[9—19]mainly focus on the research about the jamming resource allocation for multiple independent radar nodes in the space,which can be divided into two categories according to the optimization methods: classic combinatorial optimization methods and heuristic intelligent optimization methods. The former mainly includes 0—1 planning [9], closeness [10], dynamic programming [11], etc. These methods can solve the small-scale jamming resource allocation problem well, but with the increase in the scale of both opposing sides, the allocation solution space will show explosive growth, which is difficult to be solved by general combinatorial optimization algorithms, and then heuristic intelligent optimization methods[12—18]are considered for largescale jamming resource allocation problems. Liu et al. [12] solved the jamming resource allocation problem using an improved genetic algorithm with the detection probability as the evaluation metric. He et al. [13] applied an improved ant colony algorithm in jamming resource allocation and verified the applicability of the algorithm through simulation. Dai et al. [14,15] both proposed a resource allocation optimization model based on improved particle swarm algorithm, starting with the matching degree of jamming waveform in spatial domain, frequency domain and polarization mode. Wang et al. [16] chose the degree of decrease in detection probability as an evaluation metric,and adopted an improved gray wolf algorithm for the jamming resource allocation problem,which had a certain improvement in solution speed. Liu et al. [17,18]studied the solution effect based on the improved cuckoo search algorithm in the jamming resource allocation problem respectively,and their simulation results showed the potential advantages of the cuckoo search algorithm in solving the jamming resource allocation problem.In addition,Han et al.[19]proposed a new idea based on the game theory to solve the resource allocation problem, but the high complexity of the algorithm leads to low practicality.

In general, the previous research works provide valuable references for us to solve the jamming resources allocation problem.But the following points need to be further studied: (1) all the above works assume that the nodes in the netted radar system are completely independent, and do not consider the information fusion mode of the netted radar system.(2)modern radars are able to operate in multiple operating modes at the same time, but the resource allocation scheme derived from the above works only consider the search mode. (3) the proposed algorithm cannot be applied to the whole flight process of the aircraft formation. (4)Some important constraints are ignored.

The main contributions of this paper are as follows: (1) this paper focuses on the task scenario where aircraft formation penetrates netted radar system with its own jamming resources(i.e.,SSJ,Self-screening Jamming), and provides an adaptive cooperative jamming strategy.By optimizing the jamming resources allocation scheme of the aircraft formation in real time, the overall jamming effect on netted radar system is improved. In this way, the survivability and mission completion ability of the aircraft formation are improved. (2) the information fusion rules and different working modes of the netted radar system are considered,and a two-factor jamming effectiveness evaluation function is constructed based on detection probability and aiming probability.(3)An effective threestep solution method based on improved cuckoo search algorithm is provided to improve the computational efficiency of the solution strategy. (4) Some important jamming resource constraints are considered to further improve the practicality of the model.

The remainder of this paper is organized as follows: Section 2 establishes a system model of the netted radar system and introduces some necessary assumptions in this article.In Section 3,a mathematical model for optimizing the jamming resource allocation of cooperative jamming is developed under the jamming resource constraints. Section 4 proposes a three-step solution method based on dynamic adaptive discrete cuckoo algorithm(DADCS) for the above non-convex optimization model; Several simulation results and analysis are given in section 5 to confirm the advantages of the proposed adaptive allocation strategy.Finally,the conclusion of this paper and future work is discussed in Section 6.

2. Netted radar system model

2.1. Problem formulation and assumptions

Without compromising generality, as shown in Fig. 1, it is assumed that the netted radar system consists ofNmonostatic radars,widely distributed in two-Dimension space.The location of theith radar node is（xi,yi）,and each radar node is only capable of receiving and processing the signal echoes emitted by itself. In addition, each radar node has multiple modes, i.e., searching or tracking mode. On the other hand, suppose that a formation ofMaircraft equipped with their own jammer moves towards the netted radar system and evade the detection and tracking of the netted radar system through cooperative self-screening jamming. The position and speed ofjth aircraft atkth frame areandrespectively, while the jammer of each aircraft in the aircraft formation are in multi-beam jamming mode, which means that each aircraft can jam multiple radar nodes simultaneously. To represent the aircraft-radar node assignment relationship,a binary variableis introduced, that is

wherei= 1,2,…,N,m= 1,2,…,M.

For the sake of the following problem solving,here,we assume that the aircraft formation has obtained the information of the netted radar system (including radar node location, carrier frequency, pulse width, information fusion method and all relevant other parameters mentioned in this paper,etc.)before the mission,i.e.,these are priori knowledge for the aircraft formation.In fact,the above information generally can be obtained accurately through electronic reconnaissance equipment or other external intelligence approaches.

2.2. Detection probability model of netted radar system

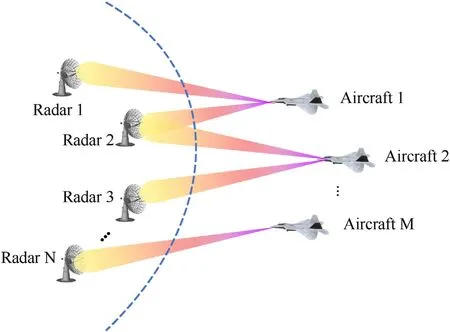
Fig.1. Description of the system model.

Detection probability [20—22] is an important performance metric that measures whether the radar can find the target in the search mode. And it denotes the probability that the radar judges the existence of the target when the target exists.First,consider the detection probability model for a single radar. Suppose radarireceives a pulse sequence during the observation time of targetm.There are two cases: (1) containing the echo signal reflected by targetmand the internal noise of the receiver; (2) containing the echo signal reflected by targetm,the internal noise of the receiver and the jamming signal emitted by targetmto radari.The power of the target echo received by radarican be acquired from the radar equation as

Similarly,the jamming power of the targetmreceived by radarican be obtained from the interference equation as

wherek1=0˙04 ～0˙1 is a constant, and θ0˙5is the radar antenna main lobe half-power width. It is worth noticed that since the jammer is configured on the protected target,it is assumed that the radarikeeps the main lobe beam aimed at the targetm,soRj,k（i,m） =Rr,k（i,m）. In order to ensure that the jamming signal enters the radar receiver successfully,it is necessary to require that the carrier wavelength of the jammer and the radar remain the same, so λj=λr.

The internal noise of the receiverPnis related to the noise figure,which can be approximately expressed by Eq. (6)

wherek0=1˙38×10-23,represents the Boltzmann constant;Ttis the equivalent noise temperature of receiver,usually set as 290 K;Δfrdenotes the bandwidth of the receiver;Fnis the noise figure of the receiver.

Combining the above formulas,it can be derived that the signal to jamming ratio (SJR) [23]received by the receiver of radariwith respect to the targetmat thekth frame is

Note that the meaning of the symbols in the above equation is the same as the previous definition.Assuming that the radar adopts noncoherent pulse integration technology and constant false alarm technology, according to the principle of radar detection, the detection probabilityof radariagainst targetmat thekth frame is a function ofwhich can be expressed as

wherePfarepresents the false alarm probability of the radar,Idenotes the number of noncoherent accumulated pulses, the definition of φ（*）is given in Eq.(10),and φ-1（x）is the inverse function of φ（*）.

Next, consider the detection probability model of the netted radar system. Here, it is assumed that the netted radar system achieves information fusion by adopting the rank K judgement criterion [24], specifically, each monostatic radar in the network makes a local judgementdi(di∈｛0,1｝)based on its own processing result of the target echoes,and sends the judgement results to the information processing center of the netted radar system. The center generates a global judgment vector D=fD（d1,d2,…,dN）based on these local judgments.There is a total of 2Npossibilities of D, i.e.

Then, the processing center makes a judgment based on the global judgment vector, and the judgment rule is noted as

Eq.(12)indicates that when there areKor more thanKradars in the net discovering the target at the same time, the netted radar system determines that the target is found.Therefore,according to the rankKjudgement criterion, the detection probability modelof the netted radar system for the targetmcan be obtained as

Table 1Detection probability model of netted radar system with different judgment criteria.

2.3. Aiming probability model of netted radar system

When the netted radar system is in the tracking mode, the parameters of the target need to be estimated to maintain stable tracking.If the measurement error of the parameter is too large,it will seriously affect the hit rate of the weapon launch, and may even turn the netted radar system from the tracking state back to the search state.Herein,in order to reflect the tracking accuracy of the netted radar system on the target in the tracking state,aiming probability is introduced as the performance metric.In this article,assuming that the netted radar system uses trajectory-based information fusion [32] for target tracking, we focus on the three parameters of distance, speed and azimuth, and assume that the measurements of above three parameters are independent of each other and approximately obey the Gaussian distribution with 0 mean.According to the SJR model of radariwith respect to targetmin Section 2.2, the mean square error (MSE) [25—30] of the measurement error of the above three parameters is given by

Next,the probability density function of the measurement error for each parameter can be obtained as

where Δr, Δv, and Δθ represent the maximum allowable upper limits of the measurement errors of distance,velocity,and azimuth,respectively. In other words, as long as the measurement errors of the parameters do not exceed the corresponding permissible range,the radar tracking system could continuously track in this dimensional parameter. By integrating Eq. (15) combined with Eq. (16),the aiming probability of the corresponding parameter is defined as

Assuming that if the measurement error of any of the above parameters exceeds the allowable range, it will cause the radar to fail in tracking the target,the aiming probabilityof the radari

with respect to targetmat thekth frame can be defined as

According to the trajectory-based information fusion, the aiming probability modelof the netted radar system with respect to targetmat thekth frame can be also expressed as

It should be noted that although Eq. (19) and Eq. (13) are the same in structure,their fusion methods are different.

3. Cooperative jamming resource allocation optimization model

Mathematically, the problem of jamming resource allocation can be transformed into a problem of optimizing the jamming effectiveness of the aircraft formation on the netted radar system under some system requirements and limited jamming resources.Specifically, the independent variables in this paper are theN×Mbinary variablesuki,m(i=1,2,…N m= 1,2, …M) mentioned in Section 2.1,Our optimization goal is that making aircraft formation achieve the best cooperative jamming effectiveness on the netted radar system by optimizing these independent variables subject to the given constraints. Since the netted radar system has different working states, here, we consider two aspects of jamming effectiveness: (1) reducing the ability of the netted radar system to detect aircraft formation in the search state; (2) reducing the tracking accuracy of the netted radar system in the tracking state so that its weapon system cannot meet launch conditions. The detection probabilityPkdnet,mand aiming probabilityPkanet,mintroduced in Section 2 are used as performance metrics to measure jamming effectiveness simultaneously. To reflect the overall jamming effectiveness of cooperative jamming and the importance of each aircraft, we set the 2 objective functions as

where ωmis the importance factor of themth aircraft, and the larger ωmis, the more important themth aircraft is.

Subsequently, the following constraints need to be considered:

(1) The number of radar nodes that each aircraft can simultaneously interfere with at each frame is finite and can be expressed as

wherePis the maximum number of radar nodes that can be jammed simultaneously by each aircraft at each frame.

(2) For the sake of limitations on computational complexity and jamming resources,the number of jammers assigned to each radar node at each moment is also limited, which can be represented as

whereQis the maximum number of jammers allocated to each radar node at each frame. It is worth noticed that the abovementioned constraints make the jamming resource allocation problem more practical.

By integrating Eq. (20)- Eq. (22) and Eq. (1), the resulting mathematical model of optimal allocation of cooperative jamming resources can be described as

4. Adaptive allocation strategy for cooperative jamming resources

4.1. Improved cuckoo search algorithm

The Cuckoo Search algorithm[33—38](CS)is a novel intelligent optimization method proposed by Yang et al., in 2009. Compared with other heuristic optimization algorithms, CS has the advantages of simple structure, few parameters, fast convergence speed and high computational efficiency, etc. The algorithm uses the bird's nest to represent the possible solution of the optimization problem, and finds the best solution by simulating the cuckoos'parasitic brooding behavior that randomly looks for the nest of other better hosts to hatch their own eggs.In the process of finding the optimal solution, the algorithm follows the three rules:

1) Each cuckoo lays only one egg at each time and randomly selects a nest to complete incubation.

2) Among the randomly generated nests, the best nests will be retained to the next generation.

3) The number of parasitic nests available to the cuckoo is certain,and the probability of the egg being found by the host of the parasitic nest isPa∈[0,1］.

As mentioned before,the optimization problem in this paper is a non-convex multi-objective optimization problem for multidimensional binary variables that subject to discrete constraints.In order to deal with this problem effectively in the following,cuckoo search algorithm (CS) is selected here. But it is worth noticed that the standard CS algorithm is used to solve real number optimization problems, which cannot be applied directly to solve this problem. Hence, the improved cuckoo search algorithm modifies the encoding method, path update strategy, adaptive probability adjustment factor and global collaborative control mechanism. The detailed improvements are as follows:

(1) Initial solution generation and encoding.

Firstly, the Logistic chaotic mapping method [10] is used to obtain the binary initial matrix solutions [uki,m］N×M, which are uniformly distributed in the solution space and satisfies the constraints.Then the initial matrix solutions are encoded with integer vectors to improve the computational efficiency of the algorithm.Let the encoded bird's nest position be x = [x1,x2,…,xN］, each subcode elementxiis an integer,and the numbers on the different digits ofxiindicate the indexes of aircrafts interfering with radari.For example,xi=3 means that radar nodeiis interfered by aircraft 3;xi=23 means that radar nodeiis interfered by aircraft 2 and aircraft 3;xi=145 means that radar nodeiis interfered by aircraft 1,aircraft 4 and aircraft 5.The detailed operation process is shown in Fig. 2.

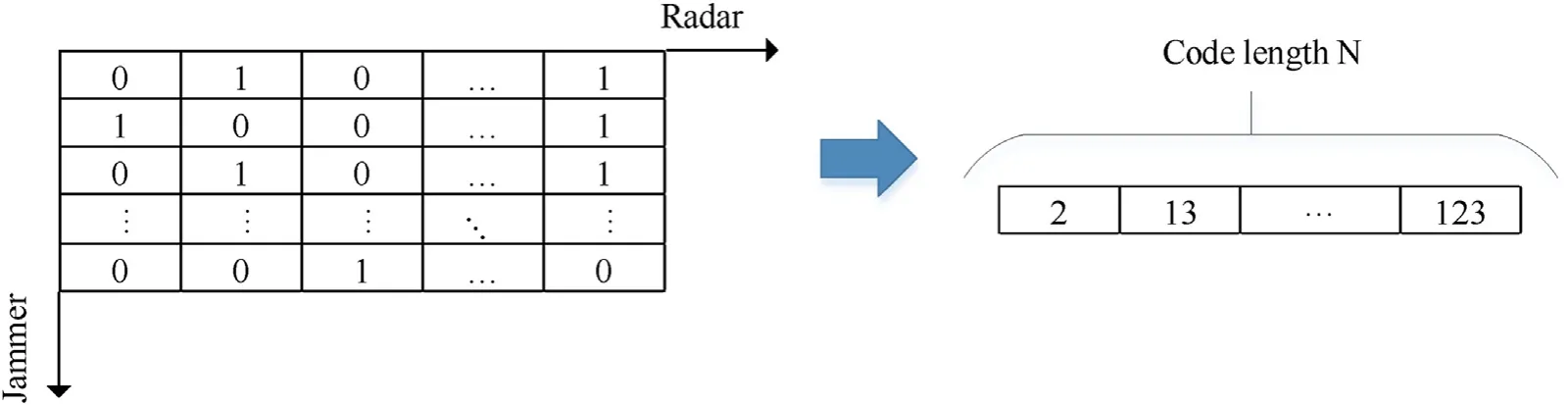
Fig. 2. Encoding process.

Fig. 3. 2-opt optimization operator: (a) Original solution; (b) New solution.

(2) Path update strategy.

The path update method of the standard CS algorithm needs to update every dimension of the nest position, which greatly increases the computational load. For this reason, the 2-opt optimization operator [39,40] and the swap-order optimization operator are introduced to extend the path update strategy and solve the contradiction between population diversity and convergence speed.

a. 2-opt optimization operator

The 2-opt optimization operator randomly selects two subcodes of the current solution and inverses their arrangement.An example is presented in Fig.3,where the 2nd and 5th subcodes are selected,and their arrangement is inversed. In this way, the new candidate solution x′=[1,5,4,3,2］ can be obtained.

b. Swap-order optimization operator

The swap-order optimization operator randomly selects two subcodes of the current solution and only swaps the positions of these two subcodes. An example is presented in Fig. 4, where the 2nd and 5th subcodes are selected, and their positions are exchanged.In this way,the new candidate solution x′=[1,5,3,4,2］is obtained. It is worth noticed that the effect of the swap-order optimization operator on the original solution is not as large as that of the 2-opt operator.

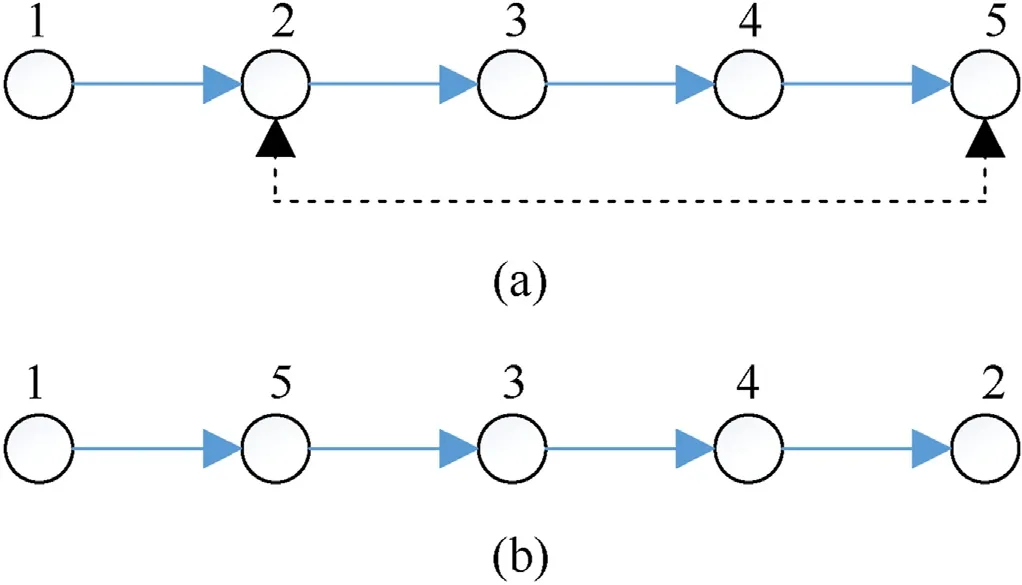
Fig. 4. Swap-order optimization operator: (a) Original solution; (b) New solution.

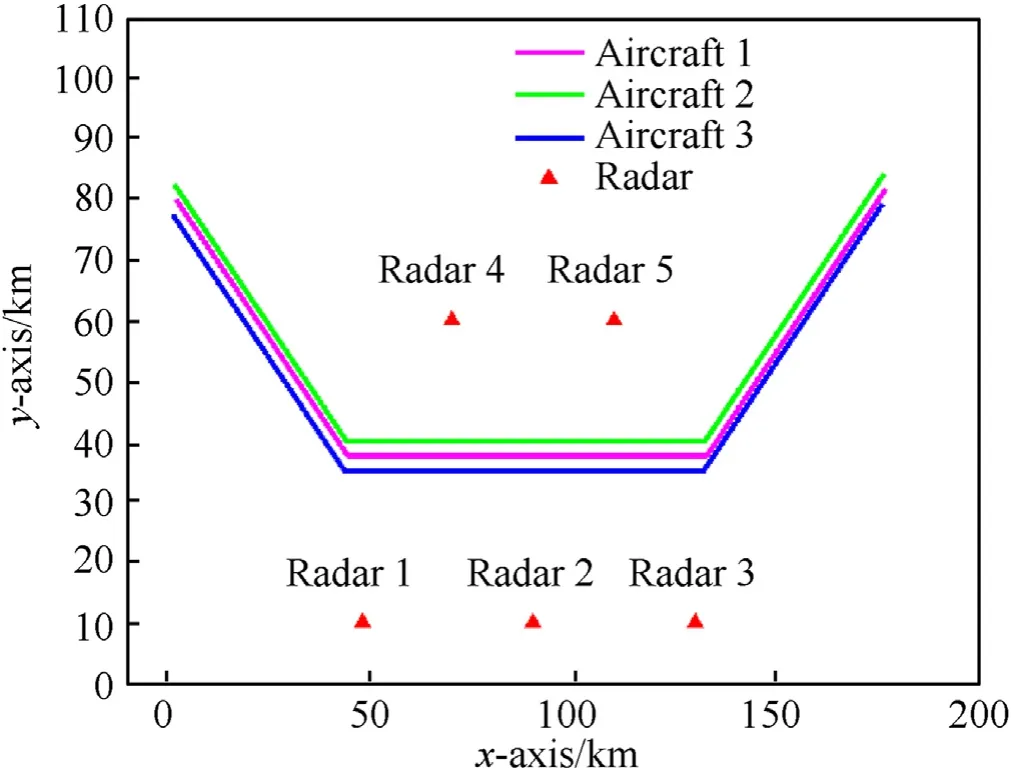
Fig. 5. Deployment of netted radar system and trajectory of aircraft formation.

(3) Adaptive probability adjustment factor.

The adaptive probability adjustment factor ρcis designed to improve the algorithm's ability of adjusting the bias of different strategies adaptively in iterations. The adaptive probability adjustment factor ρcis compared with the random numberr0(r0∈（0,1）), if ρc>r0, the 2-opt optimization operator is adopted,otherwise the swap-order optimization operator is adopted.Considering that the 2-opt optimization operator disturbs the solution more than the swap-order optimization operator, the adaptive probability adjustment factor is gradually reduced.In this way,the algorithm can increase the search range in the early stage and improve its search accuracy in the later stage.The definition of ρcis as follows

wherec1andc2are the threshold control parameters. Through a large number of experiments, the algorithm runs best whenc1=0˙3,c2= 0˙5.tis the current number of iterations, andTotis the maximum number of iterations.

(4) Global collaborative control mechanism.

When the eggs are discovered by the host, the global collaborative control mechanism is used to control the search direction of the population path and improve the utilization of the historical population information. The mechanism is expressed as

where xiand xgbestare the discovered nest and the current global optimal nest respectively, （xi,xgbest） denotes the set of transformation pairs consisting of positions corresponding to the same subcode in xiand xgbest.T（xi,xgbest） represents a transformation pair randomly selected from （xi, xgbest）, andx⊕ydenotes the learning operator, which means to exchangex's subcodes at two positions determined byy.

For example,the current global optimal nest and the discovered nest are xgbest=[1,3,4,5,2］ andx = [1,2,3,4,5］, the set of transformation pairs can be ｛（2,3）, （3,4）, （4,5）, （5,2）｝. Suppose that randomly select the first element （2,3） in the set, and swap the positions of the 2nd subcode and the 3rd subcode of the discovered nest, then get the new solution x = [1,3,2,4,5］.

Combining the above improved method and the standard CS algorithm, a dynamic adaptive discrete cuckoo search algorithm(DADCS)is proposed,and the pseudo code of the DADCS algorithm is as follows:

The improved cuckoo search algorithm (DADCS) can not only solve the established mathematical model,but also greatly improve the accuracy and convergence speed of the algorithm,which will be verified in the subsequent comparison experiments with other algorithms.

4.2. Solution strategy

In order to solve the adaptive allocation strategy for cooperative jamming resources effectively, a three-step solution method combined with improved cuckoo search algorithm is proposed.The specific process is as follows:

(1) Firstly,introduce the weights ρ1and ρ2corresponding to the two objective functions,and reformulate Eq. (23) as

where ukrepresents the solution matrixat thekth frame.

(2) Subsequently, take a three-step solution method based on DADCS algorithm to solve the strategy, which can be specifically decomposed into the following three steps.

Step 1: Atkth frame, according to the coordinates of each aircraft in the aircraft formation, calculate the geometric distanceRr,k（i,m） (i= 1,2,…N,m= 1,2,…M) between each aircraft and each radar node in the netted radar system,and set ρ1and ρ2,then update Eq. (26a) and determine the jamming resource allocation optimization model atkth frame.

Step 2: Use the DADCS algorithm to solve the above jamming resource allocation optimization model, and get the optimal allocation scheme atkth frame.

Step 3:Send the result of the optimal allocation scheme to each aircraft in the aircraft formation through the data chain, and instruct the pilot to jam the corresponding radar node.Letk=k＋1,and return to Step1.

As a result, a closed-loop adaptive allocation strategy for cooperative jamming resources is established.The general algorithm for the above solution strategy is summarized in Algorithm 2.

5. Simulation results and discussion

In this section,some simulation experiments and result analysis are conducted to illustrate the advantages of the proposed adaptive allocation strategy.Assuming that the netted radar system consists ofN=5 widely distributed monostatic radar, the location information of each radar node is shown in Table 2,and the fusion center uses the rankKcriterion (K= 2), an aircraft formation ofM=3 aircraft penetrate against the netted radar system by usingcooperative self-screening jamming. All aircrafts follow the CV model with the parameters listed in Table 3. Table 4 and Table 5 detail the relevant parameters for each jammer of the aircraft and each radar node in the radar network.Note that the performance of each aircraft and each radar is assumed to be the same here,and the importance factor for each aircraft is set as[0.5,0.3,0.2].The RCS of the aircraft is 5 m2,other parameters of the simulation are shown in Table 6.The trajectory of the aircraft formation and the deployment of the netted radar system are shown in Fig.5.In the following,we sample 100 frames uniformly from the trajectory of the aircraft formation and perform simulation analysis.

Table 2Location of each radar node.

Table 3Flight parameters for each aircraft.

Table 4Jammer performance parameters.

Table 5Radar performance parameters.

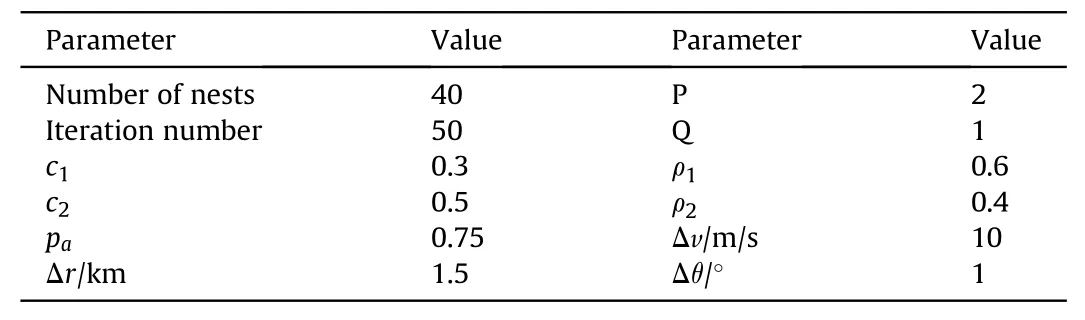
Table 6Simulation parameters.

5.1. Effectiveness verification

In this experiment,we compare the proposed strategy with the classical fixed allocation strategy and the greedy allocation strategy to demonstrate the effectiveness of the proposed strategy.The fixed allocation strategy, as the name implies, is to adopt the same jamming resource allocation scheme from the beginning to the end,here,it is assumed that the fixed allocation strategy adopts the way that flight 1 interferes with radar 1 and radar 4, flight 2 interferes with radar 2 and radar 5, and flight 3 interferes with radar 3. Thegreedy allocation strategy, also known as the “myopic” strategy,allocates jamming resources following the principle that “each radar node is jammed by the closest aircraft in the formation”.Fig.6 shows the results of jamming resource allocation by three strategies.

The marks in Fig. 6 representand the blank space indicate no allocation, different marks represent different strategies. From each subfigure of Fig. 6, it can be seen that the fixed allocation strategy is not affected by any factors,and the allocation scheme remains unchanged at each frame. The greedy allocation strategy takes into account the geometric distance between the aircraft formation and the netted radar system, and the allocation scheme at each frame will be slightly different. The proposed strategy is in dynamic change because the jamming resources is allocated adaptively in real time according to the relative positions of the aircraft formation and the netted radar system as well as the overall jamming effectiveness.

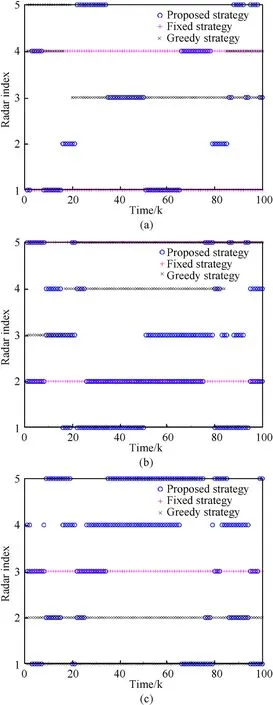
Fig. 6. Results of jamming resource allocation for (a) aircraft 1, (b) aircraft 2, and (c)aircraft 3.

In order to better illustrate the impact of the proposed strategy on jamming efficiency, the objective function values of the three strategies at different frames are given in Fig. 7. It can be clearly seen from the figure that except for the objective function values of the proposed strategy and greedy allocation strategy are the same at individual times, the objective function values of the proposed strategy are lower than those of the other two strategies, which means that compared with the fixed allocation strategy and the greedy allocation strategy, the jamming effectiveness of the proposed strategy is higher, and it can more effectively suppress the performance of the netted radar system, while improving the success rate of the aircraft formation performing the mission.

Fig. 7. Comparison of objective function values for different strategies.

It should be noted that whenk≤35, the aircraft formation is close to the netted radar system,and the distance between them is slowly approaching the minimum effective jamming distance(MEJD) mentioned in Ref. [41]. Therefore, no matter which allocation strategy is adopted, the overall jamming efficiency of the aircraft formation is gradually reduced. Whenk≥65, the aircraft formation is far away from the netted radar system, the distance between them is gradually larger than the minimum effective jamming distance, and the overall jamming effectiveness of the aircraft formation is gradually enhanced, which is consistent with the actual situation.The effect of the proposed strategy is to reduce the rate of deterioration of jamming efficiency when the aircraft formation is close to the networked radar system; and when the aircraft formation passes through the netted radar system, try to keep the jamming efficiency as stable as possible without further deterioration, which prolong the effective jamming time of the aircraft formation in the whole voyage.

Next, to quantitatively evaluate the performance of the proposed strategies, we compare the jamming effective rates of the three strategies.Here,assuming that jamming is effective when the objective function value is less than 0.5,the interference efficiency is defined as

whereEdenotes the jamming effective rate,Teis the effective jamming time during the whole flight, andTtotis the total time of flight.The jamming efficiency rate for different strategies is shown in Fig. 8.

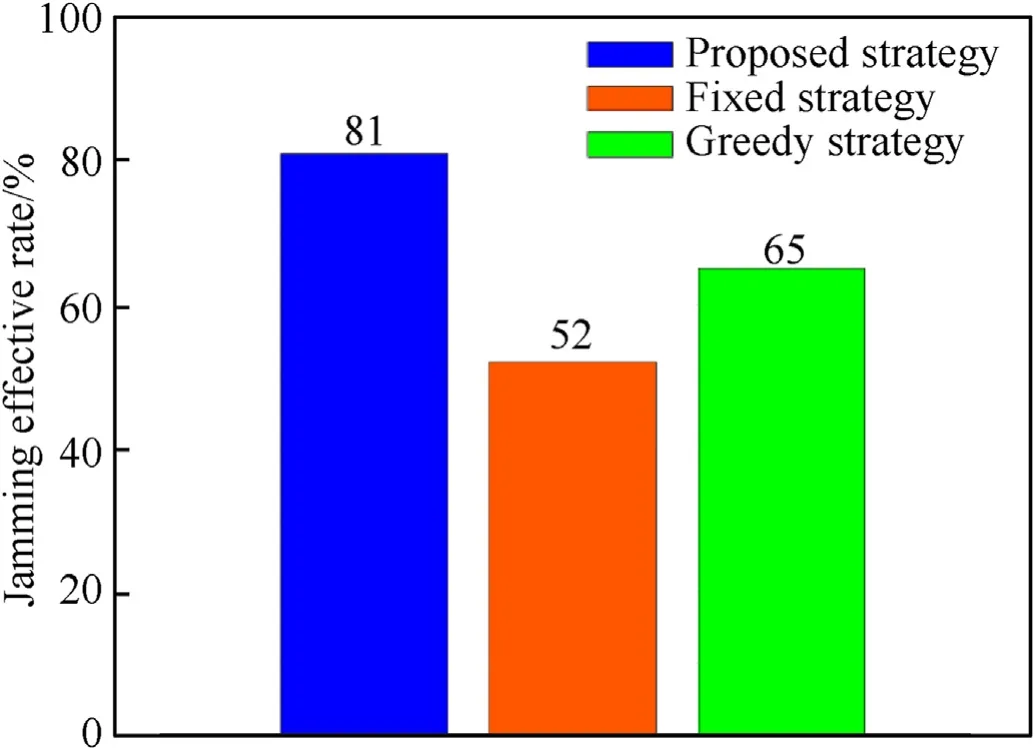
Fig. 8. Comparison of jamming effective rate for different strategies.

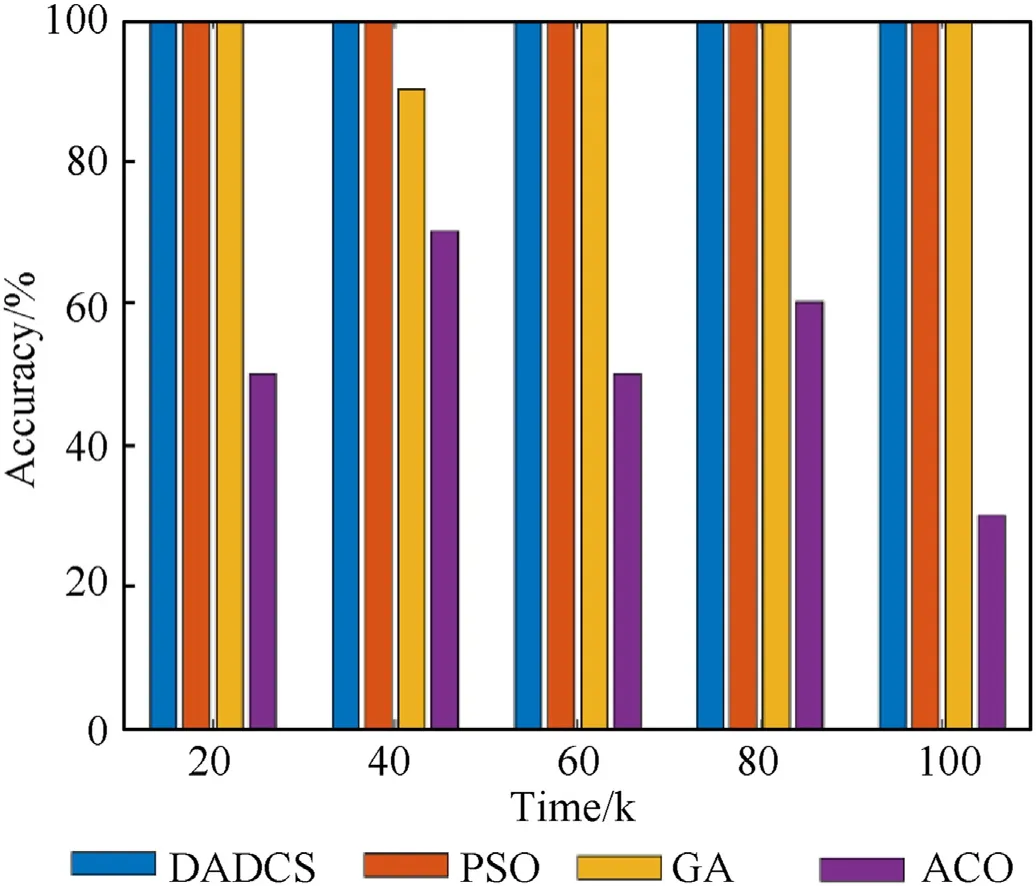
Fig. 9. Comparison of accuracy for different algorithms.

In Fig.8,the jamming effective rate of proposed strategy is 81%,and the jamming effective rate of fixed allocation strategy and greedy allocation strategy are 52% and 65%, respectively, which shows that the jamming efficiency of the proposed strategy is the best and the jamming efficiency of fixed allocation strategy is the worst, verifying the effectiveness of the strategy proposed in this paper again.

5.2. Computational efficiency analysis

In this experiment,we focus on the performance improvement of the proposed strategy in time complexity and algorithm accuracy.Since the key to solving the adaptive optimization strategy in this paper lies in solving the jamming resource allocation optimization model in Section 3 by using the improved CS algorithm(i.e.,DADCS algorithm), the time complexity and accuracy of the proposed strategy are mainly related to the iteration speed and accuracy of the DADCS algorithm for solving Eq. (26). Here, we select five frames of the whole flight process and do 100 Monte Carlo trials in each frame to compare the DADCS algorithm with the current mainstream heuristic intelligence algorithms, including genetic algorithm (GA), particle swarm algorithm (PSO) and ant colony algorithm(ACO).Fig.9 describes the accuracy distribution of different algorithms at each frame, and Fig.10 lists the total CPU time of different algorithms running for 100 frames. It should be noted that the accuracy of the algorithm refers to the ratio of the number of trials converging to the optimal solution to the total number of trials. The population size and maximum number of iterations of all algorithms are the same,and they are simulated in the environment of Windows 10 operating system with Intel(R)Core(TM) i7-11800H CPU 2.30 GHz.

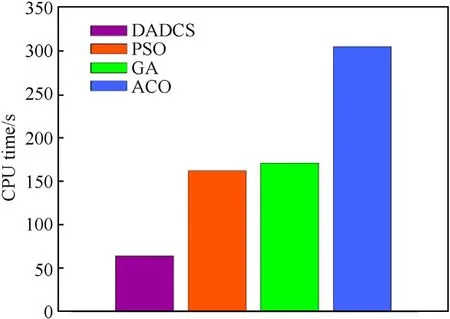
Fig.10. Comparison of CPU time for different algorithms.

From Fig.9,we can observe that the DADCS algorithm and PSO algorithm both achieve 100% accuracy at 5 frames, the GA algorithm achieves 100% accuracy at 4 frames, and the ACO algorithm has poor accuracy performance at all 5 frames,mainly because the ACO algorithm has more parameters,which are strongly correlated with each other, and relies on a priori knowledge such as pheromones that can easily lead to falling into local optimal solutions.

From Fig.10, it can be seen that the CPU time of the DADCS algorithm is much lower than that of the other three algorithms,which further illustrates that the time complexity can be significantly reduced by solving the adaptive allocation strategy using the DADCS algorithm.Moreover,it should be noted that the CPU time of the DADCS algorithm is 64.16 s,which translates to take only 0.64 s for solving the optimal policy at each frame, indicating that the method can fully satisfy the real-time requirements.

In summary, the cooperative jamming resource adaptive allocation strategy based on DADCS proposed in this paper not only provides effective jamming on netted radar system,but also greatly reduces the time complexity of this method while ensuring the accuracy.

5.3. Sensitive analysis of strategy

In this section, we investigated the effect of different weight coefficients on the jamming resource allocation strategy, and the results of jamming resource allocation for each aircraft under different weights are shown in Fig.11.

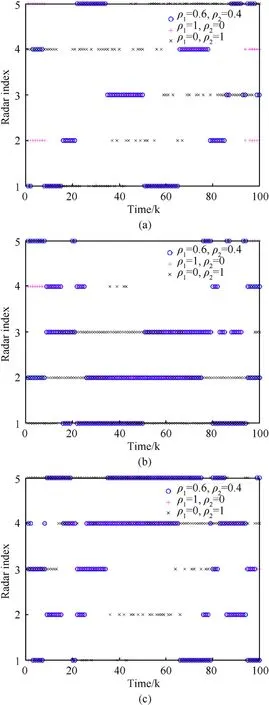
Fig.11. Results of jamming resource allocation for (a) aircraft 1, (b) aircraft 2, and (c)aircraft 3.

In Fig.11,we consider three cases by varying the values of ρ1and ρ2, where ρ1=0˙6,ρ2=0˙4 represents that the aircraft formation comprehensively considers the detection probability performance and aiming probability performance of the netted radar system,ρ1=1,ρ2=0 represents that the aircraft formation only focuses on the detection probability performance of the netted radar system,and ρ1=0,ρ2=1 represents that the aircraft formation only focuses on the aiming probability performance of the netted radar system. It can be seen from Fig. 11 that the jamming resource allocation scheme differs at each frame when the aircraft formation focuses on different performance of the netted radar system. In order to further analyze the intrinsic influence of different weight coefficients on the jamming resource allocation strategy, the jamming times of each aircraft to different radar nodes in the whole flight process are counted. The statistical results are shown in Fig.12.

In Fig. 12, the proposed adaptive allocation strategy has a common feature in the three cases, that is, the jamming times to the five radar nodes from aircraft 1 is relatively uniform,and radar nodes 1,2 and 3 will be assigned to aircraft 2 in priority,while radar node 4 and node 5 will be assigned to aircraft 3 in priority.The main reason is that according to the radar Eq.(2)and interference Eq.(4),the echo power received by the radar receiver is inversely proportional to the fourth power of the distance, and the jamming power received is inversely proportional to the square of the distance.On the premise of the same performance of the jammers,the aircraft that is farther away from the radar nodes can improve the jamming effect on the performance of the radar nodes with the advantage of distance, and the resulting efficiency ratio is higher.

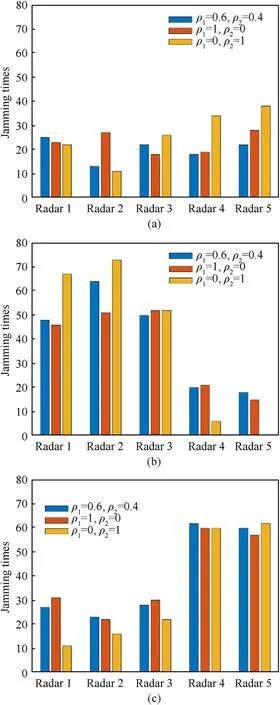
Fig. 12. Jamming times to each radar node for (a) aircraft 1, (b) aircraft 2, and (c)aircraft 3.

Meanwhile, when the aircraft formation focuses on different states of the netted radar system, the adopted jamming resource allocation scheme will have some pertinent changes. Specifically,compared with the comprehensive consideration of the detection probability performance and aiming probability performance of the netted radar system, when the aircraft formation pays more attention to the impact of cooperative jamming on the detection performance of the netted radar system,the proposed strategy will require aircraft 1 to increase the jamming times to radar node 2,and when the aircraft formation pays more attention to the impact of cooperative jamming on the tracking performance of the networked radar system,The proposed strategy will require aircraft 1 to increase the jamming times to radar node 4 and node 5, and aircraft 2 to increase the jamming times to radar node 1. It can be seen that the adaptive allocation strategy proposed in this paper can not only adjust the jamming resource allocation scheme according to the mutual position between the aircraft formation and the netted radar system, but also dynamically adjust according to the working state of the netted radar system, which further explains the necessity of considering two performance metrices in this paper.

6. Conclusions

In this paper, aiming at the resource allocation problem of aircraft formation cooperatively jamming network radar system,the following conclusions can be obtained based on the research results.

(1) An adaptive jamming resource allocation strategy based on dynamic adaptive discrete cuckoo search algorithm(DADCS)is proposed. The strategy can adjust the allocation of jamming resources in real time under the limited jamming resource constraints, making the overall jamming efficiency of aircraft formation to networked radar system maintain optimal.

(2) The different working modes of the netted radar system are considered,and the detection probability model and aiming probability model of the netted radar system are established as the performance metrics to measure the jamming efficiency.

(3) A nonconvex optimization model with discrete constraints is constructed on top of the information fusion rules of the netted radar system and the constraints of jamming resources.

(4) By improving the standard CS algorithm, a three-step optimization method is proposed. The simulation results verify the advantages of the proposed strategy and the effectiveness of the algorithm improvement.

It should be noted that the adaptive allocation strategy of jamming resources proposed in this paper is derived under the assumption that the important intelligence information of the netted radar system is completely known,but this information may not be available in practice, Besides, the strategy focuses on the allocation of beam resources, while the potential value of other resources such as power and bandwidth has not been considered.Therefore, the future work is to further investigate the allocation strategy of joint jamming resources, and consider the case where performance parameters of netted radar system are unknown,so as to expand the application scope of the proposed strategy.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work is not funded and supported by any organization or institute.