山丘区两库三站灌溉系统优化调度方法研究

罗启华，蒋晓红，陈 于，程吉林

（1.扬州大学 水利科学与工程学院，江苏 扬州 225009；2.江苏省农村水利科技发展中心，南京 210029）

0 引 言1

【研究意义】水资源短缺和时空分布不均问题已经成为限制我国地区经济社会可持续发展的主要因素之一[1-2]。在南方地区，降水量年际变化幅度很大，在一般干旱年及特殊干旱年农业、生活等用水难以得到保证。而水库（群）系统优化调度是地区水资源管理的重要内容，有效解决了地区用水问题。【研究进展】在国外，水库（群）和泵站（群）联合优化调度研究通常以系统运行成本（以泵站提水成本为主）最小为目标函数。Kim 等[3]构建“一站多库”系统优化调度模型，采用动态规划方法求解，并应用到韩国案例中，与现状调度相比，节省了泵站调度的运行电费。Odan 等[4]将实时需水预测模型、水力仿真模型和实时调度模型整合，提出了一种优化系统实时运行的新方法，并应用于巴西圣保罗州Araraquara 供水系统，实现了系统供水可靠性最大和泵站运行成本最小双重目标。Juan 等[5]构建泵站群和水库群联合优化调度模型，采用线性规划方法求解，并应用到西班牙阿尔梅里亚省的一个供水系统调度中，与原有调度相比，节省了泵站运行成本。随后Juan 等[6]兼顾泵站运行成本与泵站抽调总水量的价值成本，以二者之和最小为目标函数，构建考虑水库蒸发损失的“单库单站”灌溉系统优化调度模型，同样采用线性规划方法求解，并应用于之前的供水系统调度中，与未考虑水库蒸发损失的优化调度结果相比，节省了整个灌区供水系统的经济成本。上述国外研究是在峰谷电价或者季节电价前提下进行的，没有考虑利用本地径流对水库补水，仅通过泵站为水库补水，不涉及水库弃水问题。

在国内，水库（群）和泵站（群）联合优化调度研究通常以供水系统的用水户缺水量最小或供水量最大为目标函数。史振铜等[7]首次提出水库与补库泵站联合调度准则约束，构建“单库单站”水资源优化调度模型，采用动态规划逐次逼近法求解，并应用到江苏段“骆马湖-皂河站”工程中，与常规调度结果相比，减少了补库泵站提水量、用水户缺水量和水库弃水量。彭勇等[8]针对深圳市西部城市供水系统的铁岗-石岩水库群联合调度问题，分别采用主供水库添加联合调度线和构造“聚合水库”的方式构建供水调度模型，采用逐步优化算法（Progressive Optimality Algorithm, POA）求解，并对比分析2 种优化调度方法求解的结果，发现后者比前者优化调度效果更好。龚志浩等[9]首次考虑调水泵站年提水量约束，提出“一库两站”系统水资源优化调度模型，采用动态规划逐次逼近法求解，并应用到江苏省六合区山湖水库“一库两站”系统水资源优化调度中，与常规调度结果相比，减少了水库弃水量，增加了受水区得到的供水量。曹明霖等[10]以南水北调东线受水区江苏段及洪泽湖、骆马湖为研究对象，建立跨区域调水多水源水库群联合供水调度多情景分层优化模型，采用Lingo 软件计算不同情景下的水资源优化分配方案，最大限度地实现了区域水资源联合供水要求。

山丘区“长藤结瓜”灌溉系统，为防止干旱年份或枯水季节雨水稀缺，常以调引外来水补充山区特枯时期灌溉水源不足[11]。此前这类灌溉系统优化调度研究中[9,12]，提出的水库常规调度准则约束解决了水库和补库泵站联合调度的补库泵站提水决策问题，但是该准则约束的参数设定不合理可能会导致调度方案出现水库弃水、灌溉缺水并存的问题，故需要通过参数试验选优来实现优化调度，而这一过程会增加程序计算工作量。【切入点】无需优选参数的水库优化调度准则约束尚没有研究，另外，若提出无需优选参数的水库优化调度准则约束，它对调度方案的优化效果尚不清楚，也有待深入研究。【拟解决的关键问题】为此，针对南方丘陵山区两座水库各自有一条河道提水线，且水库间存在一条联通提水线的“两库三站”灌溉系统，首次构建“两库三站”灌溉系统优化调度模型，并首次提出无需优选参数的水库优化调度准则约束，采用基于试验选优的大系统优化方法求解优化调度方案，拟解决采用水库常规调度准则约束时因参数选取不当导致调度方案出现水库弃水、灌溉缺水并存的问题，为山丘区类似“多库多站”灌溉系统的运行管理提供参考。

1 优化调度方法研究

1.1 系统概化

山丘区“两库三站”灌溉系统如图1 所示。该系统有2 座水库、3 座补库泵站，水库1 和水库2 各自有独立的灌溉面积，在某个时段，当水库1 需补水时，考虑河道1 的可供水量，由补库泵站1 提水补库；当水库2 需补水时，综合考虑水库1、河道2的可供水量，从补库泵站2、补库泵站3 中选择补库泵站提水补库。

图1 “两库三站”灌溉系统概化Fig.1 “Two reservoirs and three pumping stations”irrigation system

“两库三站”灌溉系统常规调度易导致水库弃水、灌溉缺水并存的问题。在水权、水价、水市场交易改革积极推动的大背景下，区域水权被严格划分[13-15]，水库不能无限制地调取外来水补库，补库泵站年可供水量受到严格控制，因此，有必要对“两库三站”灌溉系统进行优化调度。

1.2 模型构建

以年内各灌区各时段灌溉缺水量平方和最小为目标函数，以系统年可供水量（包括本地径流、灌溉回归水和河道年可供水量）、补库泵站年可供水量、时段灌溉供水量、补库泵站提水能力、水库优化调度准则为约束条件，构建“两库三站”灌溉系统优化调度模型。

目标函数：

式中：F为灌溉系统各灌区各时段灌溉缺水量平方和最小值；i为时段编号；T为全年划分的总时段数；Xi,j为在i时段水库j的灌溉供水量（104m3）；Gi,j为在i时段灌区j的灌溉需水量（104m3）。

约束条件：

1）系统年可供水量约束：

式中：Kj为水库j的年可供水量（104m3）；Yj为补库泵站j的年可供水量（104m3）。Y1和Y3为给定值，应综合考虑补库泵站提水能力和河道开发利用红线的要求确定。

2）补库泵站年可供水量约束：

式中：Yi,j为在i时段补库泵站j的提水量（104m3）；Y2为补库泵站 2 的年可供水量，是决策变量（104m3）。

3）时段灌溉供水量约束：

4）补库泵站提水能力约束：

式中：Ni,j为在i时段补库泵站j的提水量上限（104m3）。

5）水库优化调度准则约束：

水量平衡方程：

水库1：

水库2：

水库库容约束：

式中：Vi,j为在i时段末水库j的蓄水量（104m3）；Li,j为在i时段水库j的来水量（104m3）；Pi,j为在i时段水库j的弃水量（104m3）；Ei,j为在i时段水库j的蒸发和渗漏水量（104m3）；Vi,j(min)为在i时段水库j的蓄水量下限，一般取值为水库j的死库容（104m3）；Vi,j(max)为在i时段水库j的蓄水量上限，在非汛期为正常蓄水位对应的库容，在汛期为调度设定的最大控制水位对应的库容（104m3）。

根据以上水量平衡方程，本文制定了水库优化调度准则，与水库常规调度准则相比[12]，Yi,j的计算式还考虑了在水库按灌溉需水量供水、补库泵站按提水能力上限补库条件下，i+1 至T各时段末的水库蓄水量未达到蓄水量下限的缺水量，由此可实现补库泵站提前若干时段提水补库，以保证各时段末水库蓄水量均满足蓄水量下限约束；此外，水库1 优化调度准则还增加了对Yi,2(先)方案调整的计算式，Yi,2(先)方案为提前知道的Yi,2方案，该准则运行结束后，获得Yi,2(后)方案，Yi,2(后)方案为对Yi,2(先)方案调整后的Yi,2方案，可帮助水库1 减少弃水量。因此，水库优化调度准则可实现参数无需改变的优化调度。水库2 优化调度准则，以Yi,3方案已知，Yi,2方案未知的情况来说明。水库j优化调度准则，优化过程中处理方法如下：

若Vi,j＜Vi,j(min)，则在i时段补库泵站j的提水量Yi,j为：

补库泵站2 的提水量Yi,2(后)为：

水库j的弃水量Pi,j为：

若Vi,j＞Vi,j(max)，则在i时段补库泵站j的提水量Yi,j为：

补库泵站2 的提水量Yi,2(后)为：

水库j的弃水量Pi,j为：

若Vi,j(min)≤Vi,j≤Vi,j(max)，则在i时段补库泵站j的提水量Yi,j为：

补库泵站2 的提水量Yi,2(后)为：

水库j弃水量Pi,j为：

式中：Cα,j为水库j从i+1 到α各时段需水量与入库水量差值之和，正值、负值分别表示水库j缺水量、余水量，（α=i+1,i+2,…,T）（104m3）；计算式为：

1.3 求解方法

该灌溉系统可分解为2 个单库子系统，由补库泵站1、外调水泵站（补库泵站2）和水库1 组成子系统1，由补库泵站2、补库泵站3 和水库2 组成子系统2。2 个子系统间存在补库泵站2 提水线的水力联系，故2 个子系统的优化调度结果需保持Yi,2方案的一致性，1 个子系统优化调度结果的Yi,2方案，可作为另外1 个子系统的已知条件。此外，使用水库2优化调度准则需知道补库泵站2、补库泵站3 其中1个补库泵站的提水方案，故采用正交试验方法来拟定Yi,3方案。在Yi,3试验方案得到后，“两库三站”灌溉系统优化调度模型就能采用大系统优化-动态规划方法求解优化调度方案。所有Yi,3试验方案得出优化调度方案后，从中选优得出灌溉系统的最终优化调度方案。

1.3.1 正交试验

补库泵站3 应提水量计算式为：

式中：Q2为水库2 各时段需水量与来水量差值之和（104m3）；Q2计算式为：

拟定5 个用水高峰时段5 月、6 月中旬、7 月中旬、8 月中旬、9 月中旬为试验因素，在这些时段找出补库泵站3 共同的可提水量范围，设计4 个提水量作为试验水平，试验水平的设计应保证有试验方案的提水量等于式（21）计算值，然后构造正交表L16(45)[16]，4 个提水量值分别用0、1、2、3 代替表示，即可拟定16 个补库泵站3 提水试验方案，详见表1。计算各补库泵站3 提水试验方案的提水量，找出提水量等于式（21）计算值的补库泵站3 提水试验方案，将其作为最终拟定的补库泵站3 提水试验方案，可进一步减少试验方案，缩小程序计算工作量和运行时间。

表1 补库泵站3 提水试验方案Table 1 Pumping test schemes of pumping Station 3 104m3

1.3.2 大系统优化

当补库泵站3 提水方案已知后，分解耦合约束式（2），变成2 个单库子系统年可供水量约束，从而可构建单库子系统优化调度模型，实现双决策变量、二维的大系统问题转化为2 个单决策变量、一维的子系统问题。大系统优化因子是Y2值，通过优化Y2值，即可优化各子系统得到的年可供水量，然后反复设定不同的Y2值，进行各子系统单独优化调度，获得对应Y2值的大系统优化调度结果。从不同Y2值的大系统优化调度结果中根据大系统目标函数值（各子系统优化调度结果的目标函数值求和）选优，即可得到优化Y2值后的大系统优化调度结果，达成大系统的优化调度。“两库三站”灌溉系统的2 个单库子系统，由补库泵站1、外调水泵站（补库泵站2）和水库1 组成子系统1，由补库泵站2、补库泵站3 和水库2 组成子系统2。2 个子系统的优化调度模型分别为：

1）子系统1 动态规划模型：

目标函数：

子系统1 的年可供水量约束：

水库1 优化调度准则约束（见j=1 的水库优化调度准则约束）。

式中：f1为灌区1 各时段灌溉缺水量平方和最小值。

2）子系统2 动态规划模型：

模型1：

目标函数：

子系统2 的年可供水量约束：

水库2 优化调度准则约束：Yi,3方案已知，Yi,2方案未知。

式中：f2为灌区2 各时段灌溉缺水量平方和最小值；Y2为大系统优化因子，取值范围为[0,max(Q2-∑Ti=1Yi,3,0)]，在该范围等步长均匀离散（104m3）；Yi,3方案通过表1 获得。

模型2：

目标函数：

子系统2 的年可供水量约束为：

水库2 优化调度准则约束：Yi,2方案已知，Yi,3方案未知。

大系统优化：提前将1 个补库泵站3 提水试验方案作为子系统2 模型1 的已知条件，然后将优化因子Y2初始值代入子系统2 模型1 中求解出子系统2 的优化调度结果；接着将子系统2 优化调度结果的Yi,2方案（Yi,2(先)方案）作为子系统1 模型的已知条件，求解出子系统1 的优化调度结果，此时，补库泵站2的提水方案为Yi,2(后)方案。

Yi,2(后)方案与之前的Yi,2(先)方案比较：若完全相同，说明水库1 无弃水，则各子系统优化调度结束，获得当前Y2值的大系统优化调度结果及对应大系统目标函数值；若不完全相同，则对Yi,2(后)方案调整，再将其分别作为子系统1 模型、子系统2 模型2 的已知条件并求解，得到当前Y2值的大系统优化调度结果及对应大系统目标函数值，此时，在求解子系统1 模型时，可忽略水库1 优化调度准则的Yi,2(后)计算式，因为之前得到的Yi,2(后)方案经过调整后，已是优化好的Yi,2方案，无须再对其进行优化了。Yi,2(后)方案调整的方法为：计算Yi,2(后)方案比Yi,2(先)方案增加的提水量，在Yi,2(后)方案中找到Yi,2(后)=Yi,2(先)的时段，在这些时段中由后至前扣除增加的提水量，若这些时段的提水量小于增加的提水量，令这些时段的提水量为0 即可，在Yi,2(后)方案中Yi,2(后)≠Yi,2(先)的时段，其提水量不用变化。调整Yi,2(后)方案提水量的目的是使其提水量匹配之前Yi,2(先)方案的提水量。

然后取不同Y2值，重复上述方法求解，获得对应的大系统优化调度结果及大系统目标函数值，至所有Y2值求解完毕后，根据所得大系统目标函数值选优，得出当前补库泵站3 提水试验方案的选优Y2值和大系统优化调度结果。

子系统优化调度。上述子系统1 模型、子系统2模型1 和子系统2 模型2 均为单决策变量的一维动态规划模型，采用一维动态规划方法求解[17]。计算过程中，把水库优化调度准则加入一维动态规划方法里。以子系统1 模型求解为例说明子系统优化调度计算流程，计算流程如图2 所示。

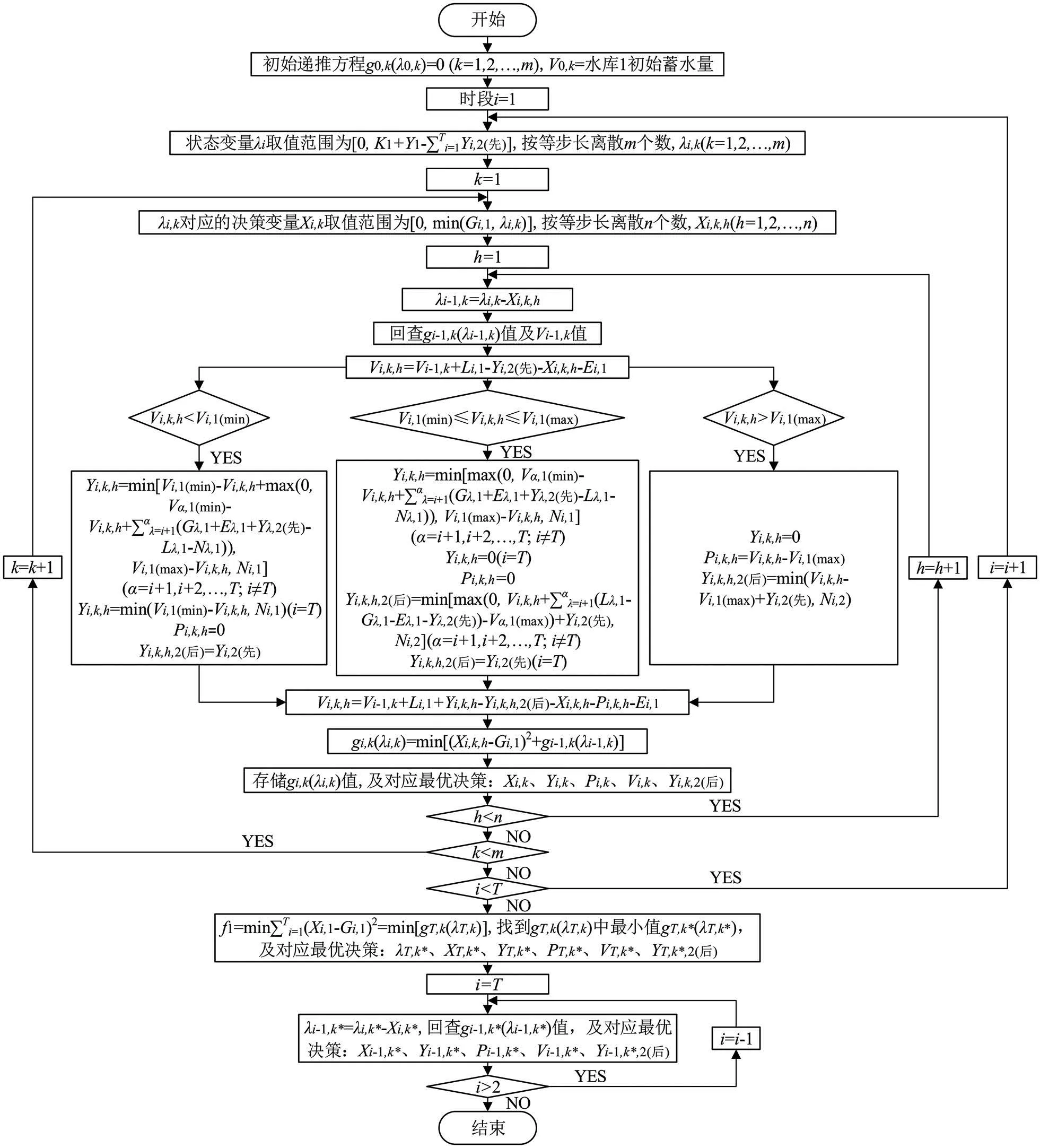
图2 子系统优化调度计算流程Fig.2 Subsystem optimization scheduling calculation process

1.3.3 试验选优

各补库泵站3 提水试验方案都按照1.3.2 小节方法求解出大系统优化调度结果后，根据大系统目标函数值选优，即可得到灌溉系统的最终优化调度方案。

2 应用实例

2.1 工程概况

在江苏省南京市六合区的蓄引提“长藤结瓜”灌溉供水系统中，山湖水库与泥桥水库各有相应的灌溉面积，山湖水库是中型水库，泥桥水库是小I 型水库。以往在干旱年份，山湖水库和泥桥水库联合调度，在某个具体时段，当泥桥水库缺水时，首先通过胡庄站提取山湖水库的水进行补库，满足灌溉需求；当山湖水库也不能满足灌溉用水量需求时，通过肖庄站提取朝阳河的水进行补库。为了减轻山湖水库调蓄压力，规划新建西凌河站，年内允许其提西凌河一定量的水给泥桥水库补库。实例工程如图3 所示，西凌河源头与朝阳河源头同为八里河，但只要明确西凌河、朝阳河各自河道水资源开发利用红线要求，与之前图1 是一致的，水库特性见表2，补库泵站提水特性见表3。

表2 水库特性Table 2 Characteristics of reservoirs

表3 补库泵站提水特性Table 3 Water lifting characteristics of pumping stations

图3 实例工程概化Fig.3 Engineering instance

2.2 来水量、损失水量和灌溉需水量

该灌溉系统各水库各时段的来水量、损失水量和灌溉需水量，采用山湖水库与泥桥水库现状水平年来水频率P=75%下的数据（表4）；水库各时段灌溉需水量为农业灌溉的需水量；水库各时段损失水量为水库的蒸发和渗漏水量。

表4 两库各时段来水量、损失水量和灌溉需水量Table 4 Water inflow, water loss and irrigation water demand of two reservoirs in each period 104m3

2.3 常规调度求解过程及结果

在干旱年份（来水频率P=75%），该“两库三站”灌溉系统常规调度时，设定西凌河站的提水时段为5 月、6 月中旬、7 月中旬、8 月中旬、9 月中旬共5 个时段，各时段均提水20 万m3，共提水100万m3。水库常规调度准则为[12]：若Vi,jVi,j(max)，则Yi,j=0，Pi,j=Vi,j-Vi,j(max)；若Vj(min)≤Vi,j≤Vi,j(max)，则Yi,j=0，Pi,j=0。该准则中需决策的参数有水库j蓄水量下限Vj(min)和水库j补水控制量Δj，按照“闲时补库，忙时供水”原则拟定参数，V1(min)、V2(min)分别设置为850 万、160 万m3，Δ1、Δ2均设置为0，得到的常规调度方案如图4 所示，常规调度数据见表5。从表5 可知，常规调度方案虽然满足肖庄站、西凌河站年可供水量约束，但是存在水库弃水77 万m3，灌溉缺水80 万m3的问题。如果能通过优化调度方法将水库弃水量减少，增加灌溉供水量，则会大大降低灌溉缺水量，促进灌区增产增收。

表5 常规调度数据Table 5 Conventional schedule data 104m3

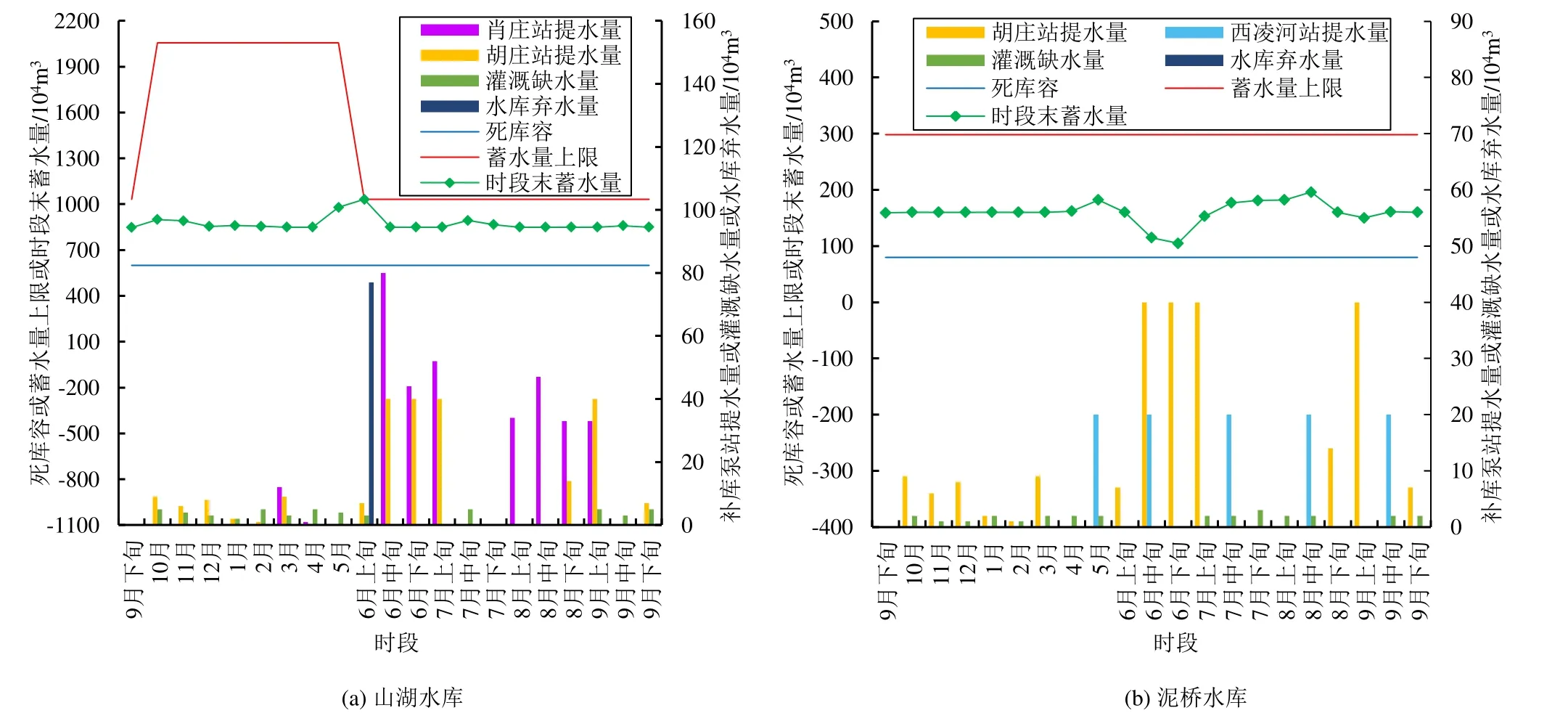
图4 常规调度方案（P=75%）Fig.4 Conventional scheduling scheme (P=75%)

若以Vj(min)和Δj为试验因素，各试验因素各设3个试验水平，通过构造正交表L9(34)设计参数试验方案，获取到相应常规调度结果如表6 所示。从表6可知，各参数试验方案下常规调度方案的山湖水库、泥桥水库最后一时段末蓄水量变化很大，很难获得统一值。而从灌溉缺水量最小的角度考虑，则以参数试验6 的常规调度方案作为优选参数的常规调度方案，如图5 所示，优选参数调度数据见表7。由表5 和表7 可知，与拟定参数的常规调度方案相比，优选参数的常规调度方案，水库弃水量减少32 万m3，灌溉缺水量减少45 万m3，取得一定优化效果，但是还存在水库弃水45 万m3，灌溉缺水35 万m3的问题。另外，山湖水库、泥桥水库的最后一时段末蓄水量相比拟定参数的常规调度方案有所下降，说明采用水库常规调度准则求解调度方案，不能很好地控制水库最后一时段末蓄水量。

表6 参数试验下常规调度结果Table 6 Conventional scheduling results under parameters tests 104m3

表7 优选参数调度数据Table 7 Preferred parameters scheduling data 104m3

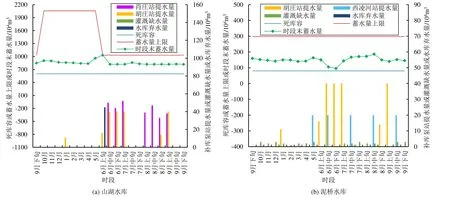
图5 优选参数的常规调度方案(P=75%)Fig.5 Conventional scheduling scheme of preferred parameters (P=75%)

2.4 优化调度求解过程及结果

由表3、表4 可知，西凌河站的年可供水量Y3为120 万m3，泥桥水库的灌溉缺水量Q2为350 万m3。由式（21）计算得出西凌河站应提水120 万m3。试验因素水平取15 万、20 万、25 万、30 万m3，分别替换表1 的0、1、2、3，制定出16 个西凌河站提水试验方案，从中找到了4 个提水量为120 万m3的西凌河站提水试验方案。

选择1 个西凌河站提水试验方案，胡庄站的年可供水量0≤Y2≤230 万m3，对其等步长均匀离散4个数。水库优化调度准则约束的Vi,j(min)取值为死库容即可，但最后一时段的Vi,j(min)取值会影响并等于优化调度方案的水库最后一时段末蓄水量，以VT,j(min)等于水库初始蓄水量为例，Vi,j(min)取值情况如表8 所示。再按照1.3.2 小节方法求解出当前西凌河站提水试验方案的优化调度方案。

表8 优化调度蓄水量下限Vi,j(min)取值Table 8 Vi,j(min) values for optimal scheduling 104m3

4 个西凌河站提水试验方案都进行大系统优化方法求解后，得到的优化调度结果如表9 所示，最终采取的优化调度方案为试验方案1 的优化调度方案，如图6 所示。

表9 西凌河站提水试验方案及其优化调度结果Table 9 Water lifting test schemes of Xilinghe station and their optimal scheduling results 104m3

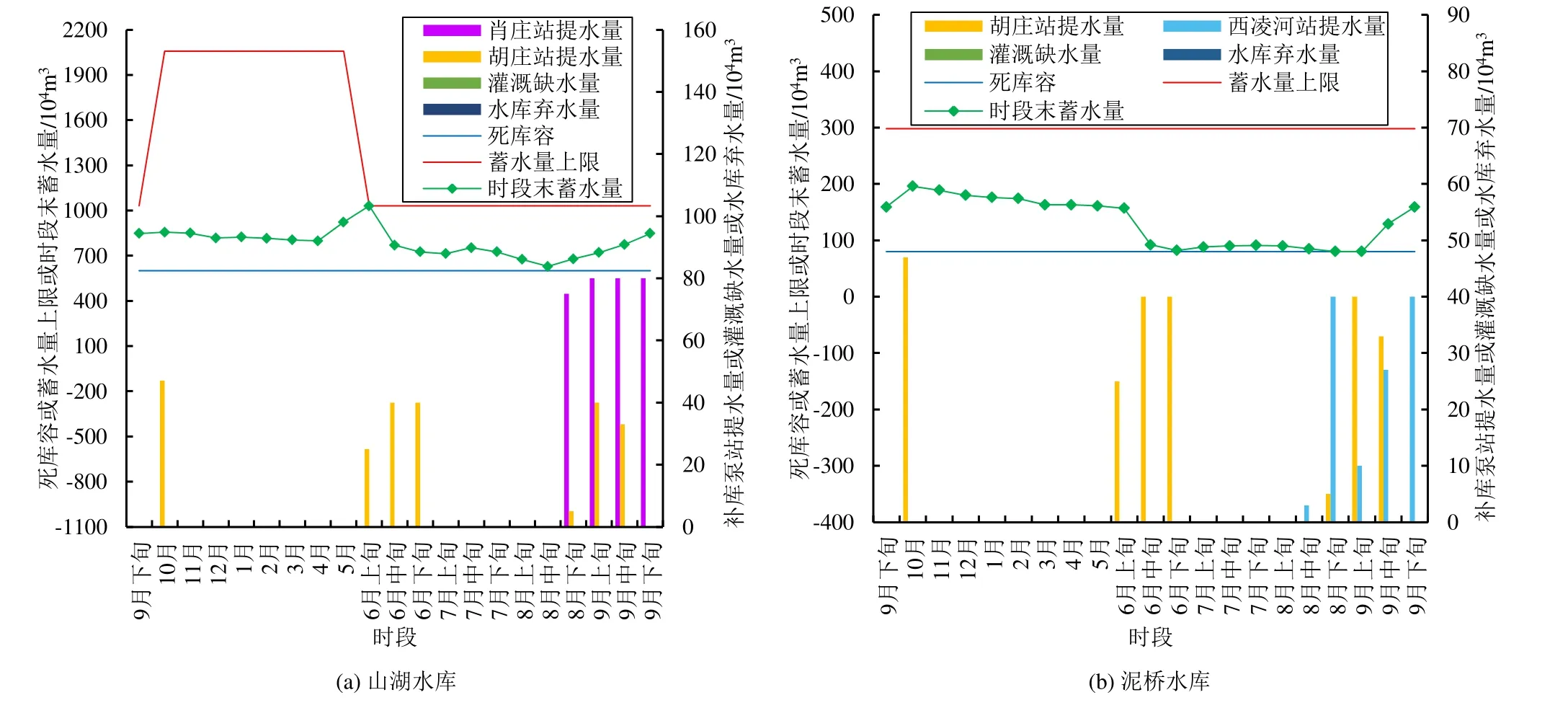
图6 优化调度方案(P=75%)Fig.6 Optimal scheduling scheme (P=75%)

从表9 可知，4 个优化调度方案，均没有水库弃水、灌溉缺水的现象，肖庄站、西凌河站分别提取的水量也满足对应补库泵站年可供水量约束，并且相同补库泵站的提水量相同，水资源在空间上的配置实现了统一。另外，这4 个优化调度方案的水库最后一时段末蓄水量均等于初始蓄水量。因此，这4 个优化调度方案均可作为案例的最终优化调度方案。因为4 个优化调度方案的大系统目标函数值均为0，按先后顺序，故选择了试验方案1 的优化调度方案作为灌溉系统的最终优化调度方案。

3 结果与分析

现状水平年来水频率P=75%下山湖水库和泥桥水库联合灌溉系统优化调度方案与优选参数的常规调度方案相比：

1）山湖灌区灌溉缺水量维持0 不变，泥桥灌区灌溉缺水量由35 万m3减少到0，山湖水库弃水量由45 万m3减少到0，泥桥水库弃水量维持0 不变。该灌溉系统水库弃水量减少45 万m3，灌溉缺水量减少35 万m3，优化调度方案实现了最大化减少水库弃水量，充分增加灌溉供水量的调度目标。同时，西凌河站提水量由100 万m3增加到120 万m3，胡庄站提水量由201 万m3增加到230 万m3，肖庄站提水量由303 万m3增加到315 万m3，河道提水量由403 万m3增加到435 万m3，并且各补库泵站的提水量也没有超过对应补库泵站的年可供水量，故优化调度方案适当增加了西凌河、朝阳河的提水量，以此来增加灌溉供水量，使得山湖水库、泥桥水库的最后一时段末蓄水量不用降低并等于初始蓄水量，实现了水资源智慧调度。此外，优化调度方案也保证了山湖水库、泥桥水库各时段末的蓄水量始终处于蓄水量上下限之间。由此可见，本文所提优化调度方法，能实现水资源在时空上的合理配置，有效减少水库弃水量，增加灌溉供水量。

2）西凌河站提水时段数维持5 个不变，胡庄站提水时段数维持7 个不变，而肖庄站提水时段数由7 个减少到4 个，补库泵站提水时段数有一定程度减少，并且各补库泵站在提水时段的提水量依然满足对应补库泵站提水能力约束。同时，肖庄站、胡庄站、西凌河站提水时段的平均提水量分别增加35.5万、4.1 万、4.0 万m3。原因在于采用水库常规调度准则求解调度方案，补库泵站时段提水量是由当前时段末水库蓄水量未达到蓄水量下限的缺水量决定的，并且补库泵站在提水时段的提水量至少为水库补水控制量，Vj(min)和Δj组合方案不同，各补库泵站提水次数也会有不同程度变化。而采用水库优化调度准则求解调度方案，补库泵站时段提水量计算，考虑了剩余时段均以水库按灌溉需水量供水、补库泵站按提水能力上限供水决策时，若有时段末水库蓄水量低于蓄水量下限，补库泵站在当前时段的提水量对应增加；若没有时段末水库蓄水量低于蓄水量下限，补库泵站在当前时段的提水量只需保证该时段末水库蓄水量达到蓄水量下限即可，从而使得补库泵站在提水时段尽可能发挥提水能力补库，这样就可大大减少补库泵站提水次数。由以上分析可知，本文所提优化调度方法，可以充分发挥补库泵站提水能力，减少补库泵站提水次数。

3）优选参数的常规调度方案中，山湖水库、泥桥水库最后一时段末蓄水量分别为819 万、145 万m3，与初始蓄水量847 万、159 万m3相比，分别下降28 万、14 万m3，合计下降42 万m3，可见，优选参数的常规调度方法难以控制水库最后一时段末蓄水量。而优化调度方案中，山湖水库、泥桥水库最后一时段末蓄水量分别为847 万、159 万m3，与初始蓄水量相同，并且水库最后一时段末蓄水量由VT,j(min)取值控制，即：VT,j(min)取值多少，水库最后一时段末蓄水量就为多少。原因在于水库优化调度准则中，补库泵站时段提水量是围绕剩余各时段的Vi,j满足对应Vi,j(min)值进行计算的，所以当VT,j(min)值确定后，补库泵站就会围绕VT,j满足VT,j(min)值的目标提水，从而使得水库最后一时段末蓄水量等于VT,j(min)值。故采用本文优化调度方法，还可以实现对水库最后一时段末蓄水量特定取值的要求。

以往两库联合灌溉系统的优化调度方法是通过对水库常规调度准则约束的Vj(min)和Δj取值拟定多个组合方案，进行试验选优来实现的[12]，而本文的优化调度方法是在水库常规调度准则约束的基础上，提出无需优选参数的水库优化调度准则约束，可减少优化调度模型的决策变量，降低模型求解难度，从而更容易获取到优化调度方案。后续可开展山丘区更复杂“多库多站”灌溉系统优化调度方法研究，增加考虑水库弃水量、补库泵站提水能耗最小等目标，以期获得更优质的调度方案。

4 结 论

1）针对南方丘陵山区两座水库各自有一条河道提水线，且水库间存在一条联通提水线的“两库三站”灌溉系统调度问题，在水库来水量、灌溉需水量时段分布不均的干旱年份，与拟定参数的常规调度方法相比，采用优选参数的常规调度方法，可以进一步减少水库弃水量，增加灌溉供水量，但是减少水库弃水量的能力有限，调度方案仍有水库弃水、灌溉缺水并存的风险。

2）与优选参数的常规调度方法相比，采用基于试验选优的大系统优化方法求解优化调度方案，更能有效减少水库弃水量，增加灌溉供水量，也更能发挥补库泵站提水能力，减少补库泵站提水次数，此外，还可以实现对水库最后一时段末蓄水量特定取值的要求。

（作者声明本文无实际或潜在的利益冲突）