齿墩长度对齿墩式内消能工水力特性影响的数值分析

张博杭，李晓娟，王嘉河，郝瑞霞，田 淳

（1. 太原理工大学水利科学与工程学院，山西 太原 030024； 2. 山西杰诚明润水利工程有限公司，山西 太原 030024）

0 引 言

突扩突缩式内消能工主要包括孔板，洞塞和齿墩式内消能工等。这类消能工的原理是通过改变消能工内部水流的过流面积，使水流在局部区域的流态发生改变，并产生掺混、旋滚，形成旋涡，使水流的一部分动能转变为热能散去。Guglielmini等［1］发现，有压管道中孔板的厚度直接影响水流的形态。张建民等［2］通过数值模拟的研究方法发现洞塞式内消能工的洞塞长度不仅对消能率有一定的影响，而且与整个内消能工的结构稳定性和空化空蚀破坏的程度有关。前人针对齿墩式内消能工［3］，做了大量的工作，发现内表面为曲面的齿墩体型较优［4］，齿墩式内消能工的面积收缩比对过流能力影响很大［5］，齿墩高度的增加会使消能率增大［6］。受到前人关于长度对孔板和洞塞式内消能工水力特性影响分析的启发，本文在齿墩式内消能工前期研究的基础上，使用Fluent 软件对不同齿墩相对长度的齿墩式内消能工进行数值模拟，以期为齿墩式内消能工的体型改善提供依据。

1 数值计算模型

1.1 控制方程和求解方法

选用标准k-ε紊流模型［7］来进行模拟计算，控制方程主要包含连续性方程，动量方程，k-方程和ε-方程，具体公式如下

连续性方程:

动量方程:

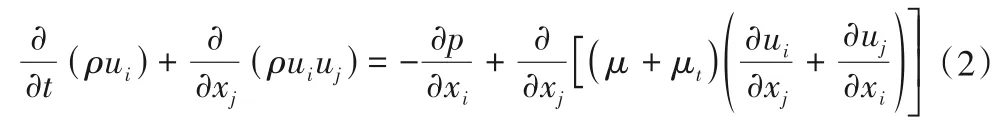
k-方程:

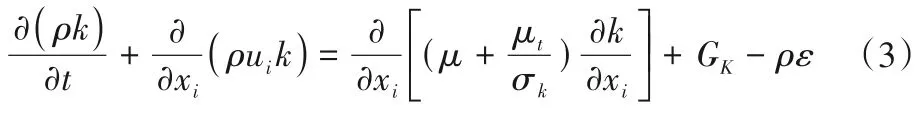
ε-方程:

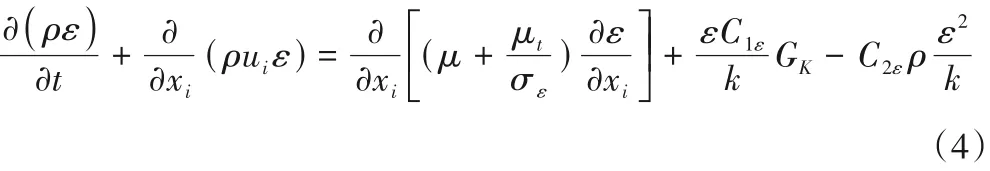
对以上微分方程（1）～（4）采用有限体积法进行离散，采用SIMPLE算法对速度和压力进行耦合迭代求解。

1.2 计算区域及网格划分

图1 试验装置图（单位:mm）Fig.1 Test device diagram

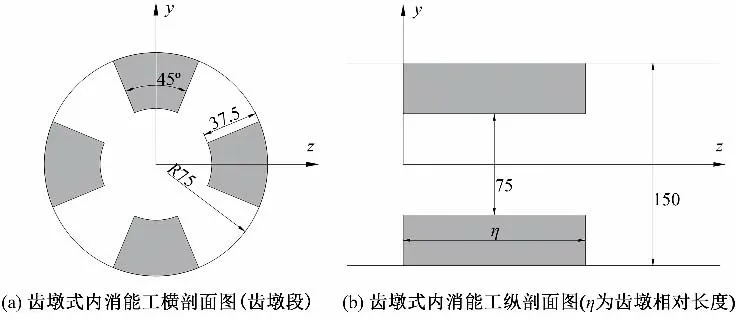
图2 试验方案尺寸示意图（单位:mm）Fig.2 Schematic diagram of the test plan size

以齿墩段入口中心点为坐标原点，垂直水流方向为y轴正方向，顺水流方向为x轴正方向建立坐标系，使用相对坐标x/D表示位置坐标。由于齿墩区域较为复杂，为使模拟更为精确，使用结构化网格进行网格划分，所画网格为尺寸8 mm 的四面体网格，三维模型总网格数为95.3 万个，网格质量满足计算要求。网格划分见图3。

图3 网格划分示意图Fig.3 Schematic diagram of mesh division

1.3 边界条件

（1）入口边界，使用速度进口入流条件，给定断面平均流速、湍流参变量等参数。其中湍流参变量中的湍流动能k与耗散率ε相关的经验公式［2］为:

式中:U为管道断面平均流速；R为管道半径。

（2）出口边界，选定压力出流，给定出口压力值。

（3）固壁边界，采用无滑移边界条件，黏性底层利用壁函数处理［9］。

2 模型验证

选取η=0.9，流量Q=40 L/s 的工况，进行物理模型试验，得到其时均压强和中心轴流速等数据，将数值模拟计算结果与测得的物模试验数据进行对比（以齿墩段入口处作为坐标原点，顺水流方向为正方向），验证对比图见图4。

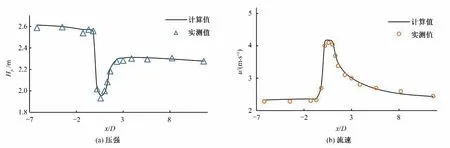
图4 计算值与实测值对比图Fig.4 Comparison of calculated and measured values

根据图4可知，计算的压强和流速与实测值基本一致，误差均在5%以内，表明本次构建的数值模型模拟结果可靠，可用于后续研究。

3 模拟结果与分析

3.1 齿墩长度对中心轴流速的影响分析

图5 为Q=30 L/s 时不同齿墩相对长度（以η=0.1、0.5、0.9 和2为例）的齿墩式内消能工的中心轴流速分布。

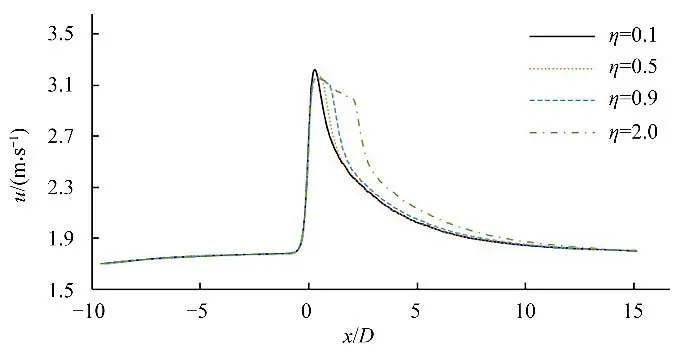
图5 中心轴流速分布图Fig.5 Flow velocity distribution map of central axis

由图5可知，在相同流量时，不同相对长度齿墩式内消能工中心轴流速分布规律基本一致，在齿墩段进口前较为平稳，进入齿墩后，由于过流面积的减小，水流流束受到挤压，流速跳跃式增加，并达到峰值，随后流速在齿墩段内缓慢下降，经过齿墩出口后，过流面积增大，流速快速下降直至恢复平稳。各方案稳定后中心轴流速均为1.82 m/s，断面流速分布呈指数型，中心轴流速略大于断面平均流速，为断面平均流速的1.07 倍；η=0.5、0.9、2的峰值流速基本相同，均为3.16 m/s，是管道断面平均流速（1.7 m/s）的1.86 倍，其峰值流速位置均出现在齿墩进口后0.38D处；η=0.1 时峰值流速最大，为3.22 m/s，高于其他相对长度的峰值流速，原因可能是当η=0.1 时，齿墩相对长度过短，在管道中的作用类似于薄壁堰，其顶部与水流接触区域较少，对水流的顶托作用小于其他长度的齿墩，同时，水流由突缩段马上进入突扩段，收缩扩展变化突然，有别于其他相对长度的情况。

3.2 齿墩长度对过流能力的影响分析

齿墩式内消能工过流能力的大小可以用流量系数来反映，流量系数的表达公式为

选取齿墩段前的断面x/D=-4 为断面1，以及齿墩段后水流稳定的断面x/D=12 为断面2，其中ΔH表示断面1 和断面2 之间的水头差，根据公式得出典型流量下流量系数随齿墩相对长度的变化，如图6所示。

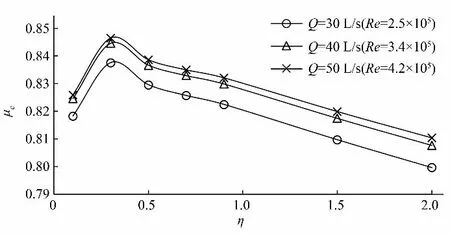
图6 流量系数随齿墩长度的变化Fig.6 Variation of flow coefficient with length of tooth-block

由图6 可得，相同齿墩相对长度下流量系数随着流量的增大而增大，但随着流量的增大，流量变化对流量系数的影响减小，主要原因是当流量Q=30 L/s 时，雷诺数为2.5×105（水温为20 ℃），管道水流处于紊流过渡区，流量系数受雷诺数和齿墩形状尺寸的影响，流量变化对流量系数影响较大；随着雷诺数的增加，当Q=50 L/s时，雷诺数为4.2×105，水流处于紊流阻力平方区，流量系数与雷诺数无关，仅与齿墩形状尺寸相关，流量系数基本保持不变。不同流量下流量系数随齿墩相对长度的变化规律基本相同，流量系数随着齿墩相对长度的增加先增加后减小，η=0.3时，流量系数最大；η≤0.9的区域内，曲线向上凸起，流量系数对长度变化较为敏感，选择η=0.9，Q=30L/s 时的流量系数0.82 作为标准，流量系数大于0.82 的相对长度范围为0.2～0.9，此相对长度范围内的流量系数较大，过流能力较优；η≥0.9后，流量系数随齿墩相对长度增加均匀减小，说明齿墩长度增加到一定程度后，过流能力逐渐下降。

3.3 齿墩长度对中心轴和壁面时均压强的影响分析

计算得出管道中心轴和管道边壁处（y=53 mm、z=53 mm 且与x轴平行的直线处）的时均压强值，其中相对坐标x/D为横坐标，以齿墩段入口中心处作为横坐标原点，顺水流方向为正方向，将时均压强换算为对应的水头H（P/γ）作为纵坐标，分别模拟计算得到同一流量下（Q=30 L/s）不同齿墩长度的齿墩式内消能工的时均压强沿程分布曲线（以η=0.1、0.5、0.9 和1.5 为例），如图7所示。

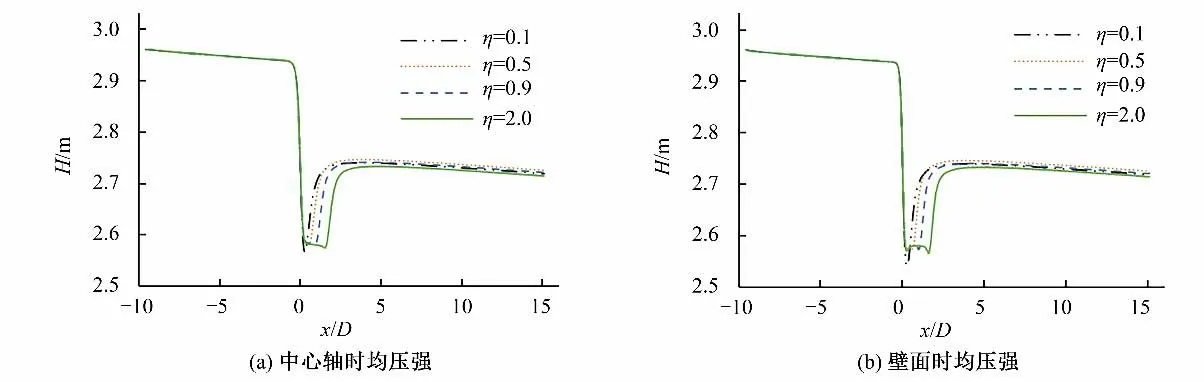
图7 Q=30 L/s时均压强分布Fig.7 Average pressure distribution at Q=30 L/s

由图7可知，在相同流量时，相对长度不同的齿墩式内消能工中心轴和壁面时均压强均是在齿墩段进口前较为平稳，齿墩进口处由于断面突缩，过流面积减小，时均压强骤减，在齿墩段内时均压强沿程缓慢下降，直至齿墩出口处达到最低点，经过齿墩后，过流面积恢复，压强逐渐上升，直至达到平稳状态。中心轴时均压强从最小值到恢复平稳的位置随着齿墩长度的增大而逐渐靠后，但各方案齿墩后时均压强恢复长度随齿墩长度的增加略微减小；除η=0.1 外，随着齿墩相对长度的不断增加，三种齿墩相对长度的中心轴和壁面时均压强恢复平稳后的值减小，说明齿墩长度对齿墩后时均压强分布有一定影响；在模拟范围内，相对长度η=0.1 时中心轴时均压强和壁面时均压强最小值均最小，分别为2.57 m和2.54 m，表明该相对长度下突缩局部水头损失最大；不同相对长度的壁面时均压强分布相较于中心轴时均压强分布，齿墩进出口两侧存在两个向下的凸起，原因是齿墩进出口边壁处由于产生旋涡导致存在低压区。

3.4 齿墩长度对消能特性的影响分析

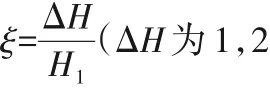
图8 消能率与齿墩长度的关系图Fig.8 Relationship between energy dissipation rate and tooth-block length

由图8 可得，在流量Q不同时，齿墩相对长度相同如η=0.9时，流量30、40、50 L/s 的消能率分别为7.1%、13.3%、23.8%，说明流量越大，齿墩前后的局部水头损失越大，其消能率也就越大；流量Q相同时，消能率随着η增加先减小后逐渐增大，η=0.3时消能率最小，相对长度η超过0.9 后，消能率较大且此后消能率变化趋于平稳，随着长度增加消能率变化不大，因此实际应用中相对长度应小于0.9。

3.5 齿墩长度对紊动能的影响分析

图9 为同一流量下（Q=40 L/s）下，z=0 截面上不同齿墩相对长度（η=0.1、0.5、0.9和2）的紊动能k的沿程分布。

图9 Q=40 L/s下不同相对长度的紊动能分布Fig.9 Turbulent kinetic energy distribution with different relative lengths at Q=40 L/s

由图9 可得，紊动能波动较大的区域出现在齿墩突缩段和突扩段的边壁处，其中齿墩段后侧以管道中心线为对称轴形成两个较大的旋涡区，该区域内紊动能数值较大，能量耗散明显，是内消能工消能的主区域；在模拟范围内，不同相对长度齿墩的突扩段旋涡区中心均出现在齿墩段后约0.23D处，且该区域的长度随着齿墩相对长度的增加逐渐减小；随着突扩段的沿程增加， 齿墩后侧旋涡区紊动能持续衰减，其断面分布逐渐均匀，最终完全恢复平稳；在模拟范围内，相对长度η≥0.9 时，突缩段旋涡区和突扩段旋涡区发生分离，且分离后的突缩段旋涡区长度不随齿墩长度的变化而变化，恒为0.87D，表明当齿墩长度大于0.9D时，突缩段和突扩段旋涡区不相互影响，多余的长度对消能的作用仅由沿程水头损失产生，这也解释了相对长度大于0.9后消能率趋于平稳的原因，因此较优长度应小于0.9D。

3.6 断面流速分布及回流区长度

为了进一步探究不同齿墩相对长度对流场特性的影响，使用Tecplot 后处理软件对Q=30 L/s 时各方案纵剖面的轴向流速进行分析，以η为0.1、0.5、0.9 和2 为例，由于齿墩段附近流速分布较为复杂，绘制齿墩附近局部断面（-1.5D至4.3D范围）流速矢量图，见图10。

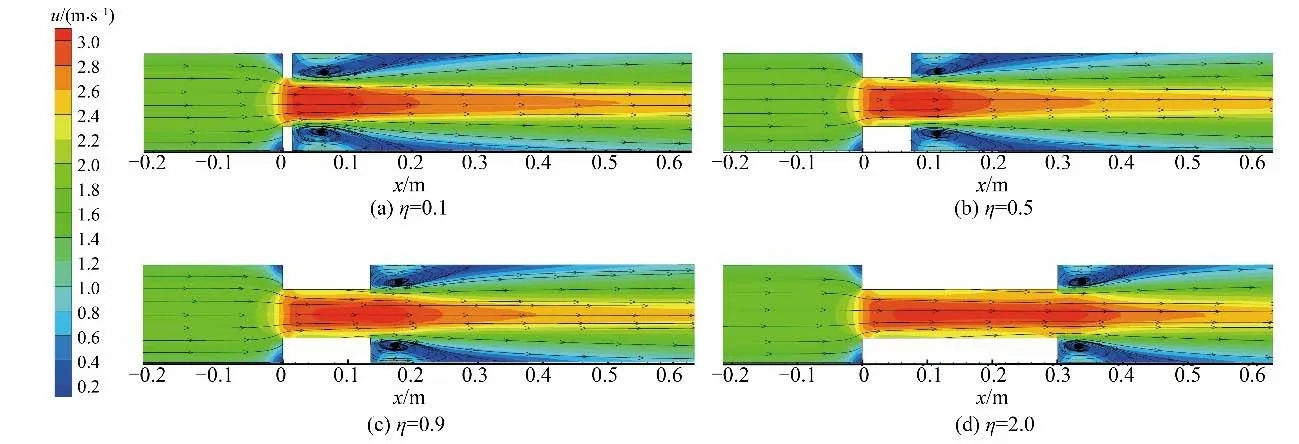
图10 断面流速矢量图Fig.10 Sectional velocity vector illustration

由图10 可知，在齿墩段的前方区域流线弯曲变形较为强烈，由于过流面积的减小，流线被迅速挤压，该区域流速显著增大。齿墩段区域内，流线变密，管道中心处流速最大，水流流过齿墩段后断面流速逐渐恢复均匀，中心轴附近流速始终大于边壁流速，且其附近的速度梯度变化十分明显；随着齿墩相对长度的增加，中心轴处的高流速区（u≥3 m/s）长度逐渐增加；齿墩前后两侧的直角边壁处均存在低流速区（u≤0.8 m/s），齿墩后方拐角处与管道中心区域的主流束产生分离并形成扁平的回流区，其高度略低于齿墩，该区域为能量转化和耗散的主要位置。

回流区长度与内消能工的空化特性密切相关［10］，通过分析不同齿墩相对长度的流速矢量图，得到不同齿墩相对长度的齿墩式内消能工的回流区长度，见表1。

表1 回流区长度Tab.1 Length of reflow zone

由表1 可得，随着齿墩相对长度η的增加，回流区长度变短，其抗空化性能逐渐提高，有利于内消能工结构的稳定。

4 结 论

在前期齿墩横截面形态和尺寸研究基础上，通过数值模拟的方法，对不同齿墩长度的齿墩式内消能工的压强分布、流速分布、过流能力、紊动能等进行了分析，获得以下结论。

（1）相对长度在0.2～0.9范围内齿墩式内消能工的过流能力较好，且其消能率较大。

（2）当相对长度大于0.9 后，突缩段与突扩段旋涡区域产生了分离，长度再增加对消能起的作用可忽略，因此齿墩相对长度不宜大于0.9。

（3）推荐齿墩相对长度0.2～0.9为齿墩较优长度范围。后续可通过物理模型试验对结论进行验证并进一步优化。