复式分汊水槽分汊口水流运动特性
闫晓楠,朱殿芳,郭志学,张 婧,李润祥
(1. 四川大学水力学与山区河流开发保护国家重点实验室,四川 成都 610065; 2. 成都市市政工程设计研究院,四川 成都 610023;3. 西华大学,四川 成都 610039)
0 引 言
天然河流按照形态和动态特征,通常分为4 种河型:游荡型、分汊型、弯曲型和顺直型[1]。在我国,分汊型河流分布相当普遍,黑龙江和松花江的许多河段普遍发育分汊型河道。分汊型河道的水流运动特性是诸多因素综合作用下形成的,作为天然河流中一种常见的河型,对于其水流特性进行研究具有十分重要的意义。
目前,许多学者对分汊河道研究取得了不少成果。Taylor[2]通过水槽试验,建立了直角分汊槽水流比与水深之间的关系;Reynolds 等[3]和Ramamurthy 等[4]均对Fr数和水深进行研究,分别建立了他们之间的联系。国内学者也在分水分沙公式的建立上做了许多深入研究。丁君松[5]以过水断面面积、平均水深及河床糙率推导出分流比的计算公式,通过分析实测资料,建立了分沙模型;韩其为[6]、余文畴[7]、秦文凯[8]、余新明[9]、童朝锋[10]等在丁君松分沙模型基础上,进一步完善了分沙模型。
分汊型河道一般由顺直段、分汊段和汇流段组成,边界条件极其复杂,其水流特性与顺直和弯曲河道相比,具有自身的独特性。水流在分汊口分汊,流线方向改变剧烈,水流结构复杂,对河道演变起到重要作用,因此许多学者对分汊口的水流运动特性进行了探索。Neary 等[11]对直角分汊明渠不同水深处的流场进行了测量,发现分汊口表、中、底层水流结构具有较大差异。Barkdoll[12]、Ramamurthy[13]、童朝锋[14]等测量了明渠分汊流的流速分布等,发现明渠中存在显著的二次流。
分汊口部分关注较多的是分汊明渠,分汊明渠的水流特性研究成果在一、二维上较为丰富,三维水流结构的探究仍值得深入。此外,在天然河流中,分汊河道一般为复式断面。然而前人对于分汊口的水流特性的研究是简化为矩形过流断面进行的,无法得到较为符合天然实际的分汊口三维水流结构。因此,本文拟通过顺直复式分汊河道水槽试验,探索分汊口水流在复式断面耦合作用下的运动特性,尽可能贴切反映天然河道分汊口水流运动。
1 试验介绍
试验在四川大学水力学及山区河流开发保护国家重点试验室中进行,采用钢化玻璃边界。试验水槽长12 m,宽2 m,高0.5 m,比降为1‰,河道床面用水泥抹光。模型上游段为单一的复式河道,长3 m,经分流段进入汊道段。模型中段布置两侧带有滩地的江心洲,左右汊河道断面均为单一复式断面。在试验模型中,江心洲长4 m,宽0.6 m,高0.2 m,滩槽宽度比为2.5∶1,左右汊宽度比为1∶2。汊道段下游进入汇流段,重新恢复为单一复式断面。汊道段主槽边界与上下游主槽边界均由弧线顺滑衔接。试验模型平面布置如图1所示。
本次试验利用薄壁三角量堰进行流量调节,通过下游侧叶式尾门调节下游水位条件,尾部沉沙池为水流出口。此外,为使水流进入水槽时尽可能平顺,在进水口处布置了花墙,并在花墙中布置了多排平水管。
试验共布置7个测量断面,以测量断面为界,同时考虑水槽的形态变化,将试验水槽分为上游段、分流段、汊道段、汇流段、下游段。考虑到分流段边界条件变化较大,该段测量断面进行了加密布置。测线沿断面布置,同样在分流段进行了测线加密。每条测线上布置了沿水深共布置12个测点。
试验采用声学多普勒流速仪ADV测量流速,纵向流速向下游为正值,横向流速指向左岸为正值,垂向流速向上为正值。试验中利用三角堰进行流量调节,使用超声波水位仪测量水深。对于相同的边界条件,选用了65、75、85 L/s 共3 个流量进行试验。试验工况见表1。

表1 试验工况Tab.1 Experiment cases
2 断面平均流速沿程分布
对测量ADV测点数据整理计算,通过式(1)和式(2)计算得到垂线平均流速(up),通过垂线分割法和式(3)求得断面平均流速V。75 L/s 流量工况下,断面平均流速的沿程分布如图2所示。
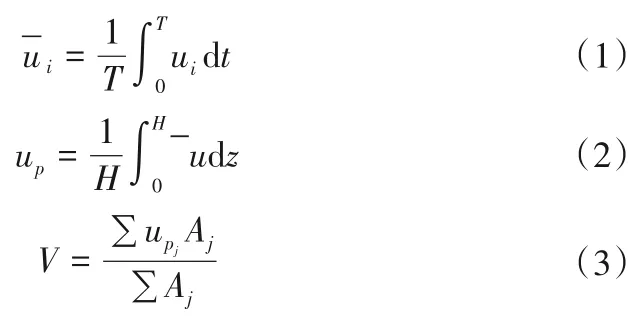
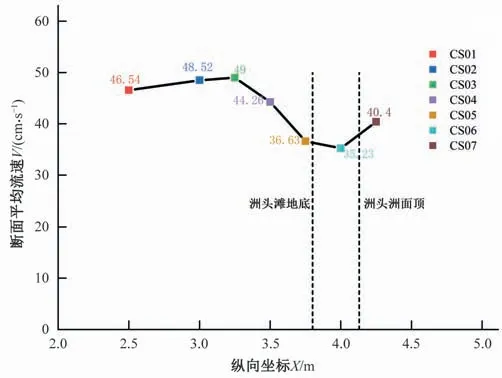
图2 断面平均流速沿程分布(A2工况)Fig.2 Average velocity distribution of streamwise (Case A2)
式中:ui为各测点的瞬时流速分量为各测点的时均流速;T为每个测点的测量时间;H为测点处的水深值;Aj为各条测线对应子区域的面积。
从图2 中可以发现,CS01 到CS03 水流受到下游分流的影响,断面平均流速沿程增大。这与罗福安[15]在直角分水口水流形态的实验研究结论一致。在CS03 到CS06 间,由于江心洲洲头的阻水作用强烈,虽然断面展宽,但局部区域水位却有所壅高,水流流速减小,甚至出现回流,断面平均流速沿程显著减小。从CS06 到CS07,水流分流绕过江心洲,断面束窄,流速增大,故断面平均流速有明显增大。这表明,在江心洲洲头分汊段,水流流速受到边界条件的显著影响,流速的急剧变化可能对江心洲洲头附近的河道形态塑造起到了重要作用。
3 相对流速垂线分布
试验中,顺直段布置了CS01~CS03 三个断面,分流段测量断面为CS04-CS07,共4 个断面。相对流速的表达式为U/V,其中U为测点时均流速。相对水深Hr的表达式为Hr=zp/H(y),其中zp为测点处水深,H(y)为断面y位置处的垂线水深。本文采用以上两个无量纲数分析水槽流速的分布特征。A1、A2、A3三个工况下,分汊口水流相对流速的垂线分布规律大致相同。因此本节将以A2 工况为例,简要介绍水流相对流速的垂线分布规律。A2工况下,顺直段和分流段断面不同位置垂线流速分布分别如图3~5所示。
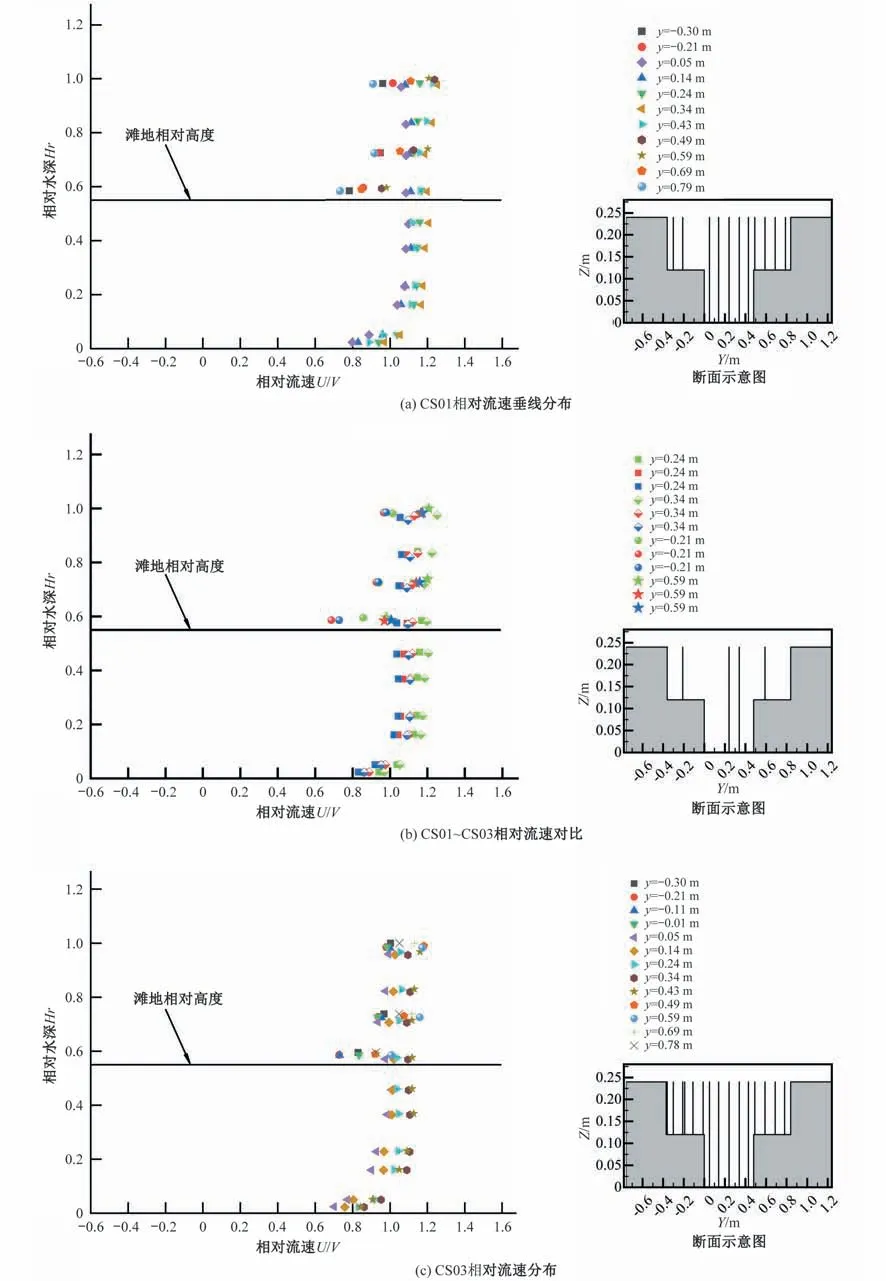
图3 顺直复式段流速分布图Fig.3 Velocity distribution of straight compound section
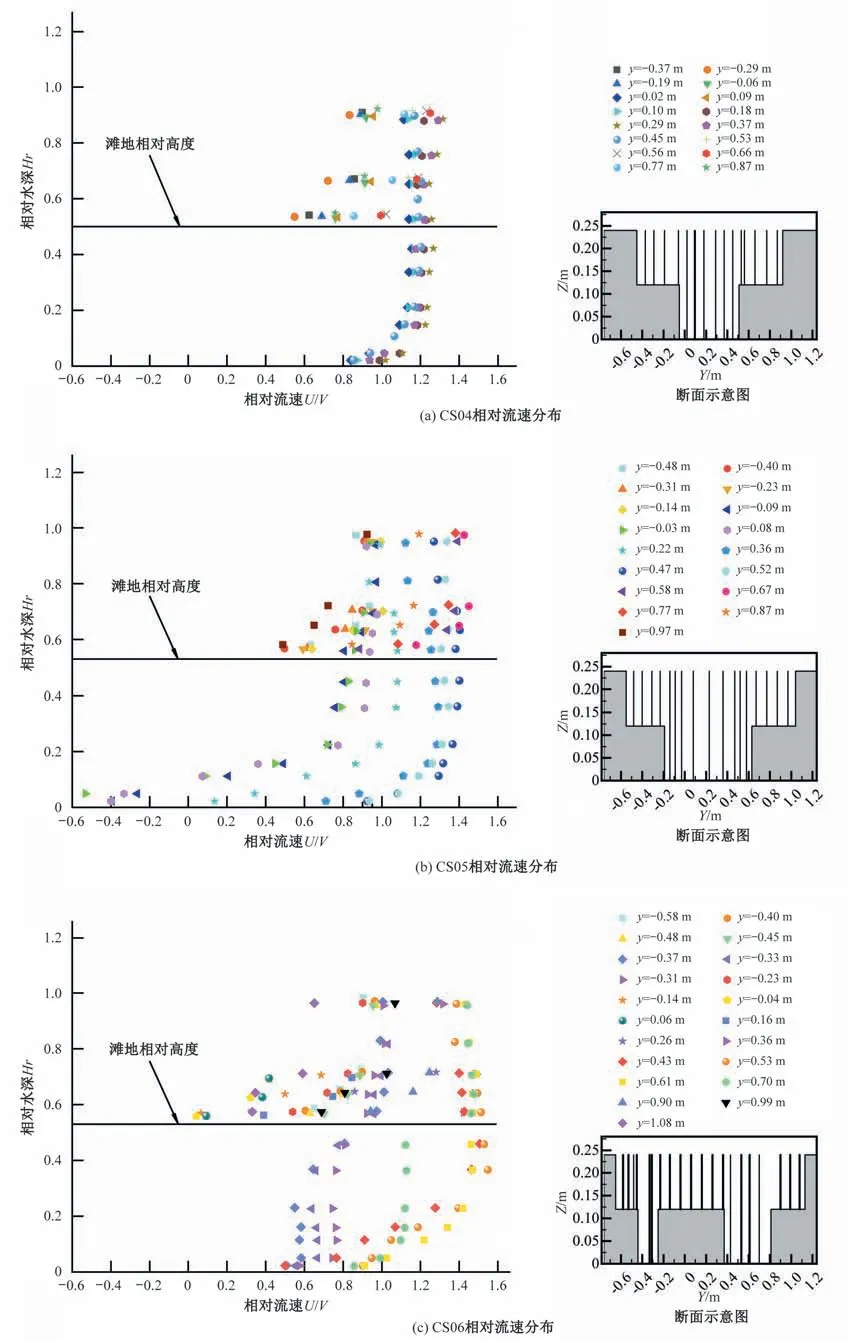
图4 顺直复式段流速分布图Fig.4 Velocity distribution of branching section
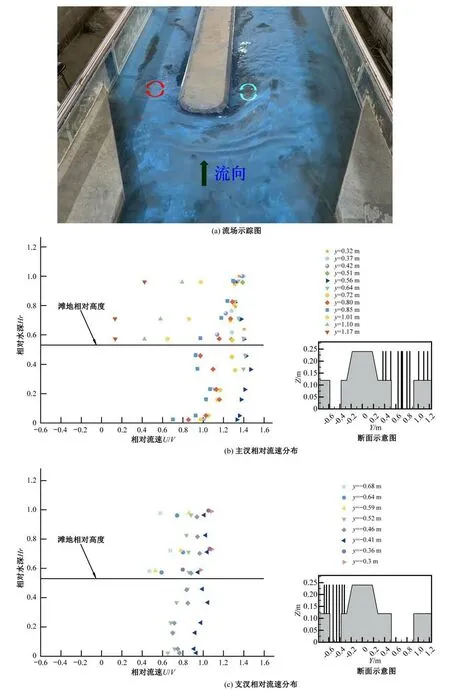
图5 CS07流速分布图Fig.5 Velocity distribution in CS07
3.1 上游顺直段相对流速垂线分布
从图3(a)中可以看出(以江心洲洲头为y轴零点),上游复式断面CS01 水流主槽和滩地相对流速垂线分布大致满足对数分布:从底部到水面,相对流速随水深增大。靠近主槽边壁和两岸边壁的水流(y=0.05,0.14,0.79 m)由于滩槽交互作用和受到边壁的影响,水流发生横向交换,最大相对流速不再位于水体表面,而是有一定程度的下降。主槽流速相对于滩地流速大得多,这符合复式河道水流“主槽大,边滩小”的特征[16],反映出主槽水流的主导作用。此外,还发现滩槽交界处(y=0.49 m)滩地流速有明显的增大,这是由于复式河道中主槽与滩地之间发生动量交换所致。测线与江心洲洲头横向距离越大,主槽流速越大,这表明此断面水流流速已经受到了江心洲分汊的影响。这表明,在受到江心洲洲头分汊的影响后,虽然上游复式断面流速垂线分布仍大致符合复式河道的水流规律,但主汊一侧水流由于下游分汊水流的影响,流速显著增大。这可能是造成分汊河道主支汊分流分沙的差异性的重要因素,深刻地影响着分汊河道的演变。
CS01、CS02、CS03 断面均为单一复式断面,且逐渐靠近江心洲。从图3(b)中可以发现,主槽垂线上整体相对流速减小,反映出江心洲的阻水作用往下游逐渐增大。同一断面主槽主汊一侧垂线流速均沿横向增大,这些反映出江心洲的作用在纵向与横向上均有所表现。
3.2 分流段相对流速垂线分布
断面展宽后,CS04 断面流速分布仍大致满足对数分布,但滩地流速与主槽流速的差距增大。由于江心洲的阻挡作用显著,洲前水位仍会壅高,滩地相对高度降低,展宽段断面平均流速也有显著减小(见图2)。华祖林[17]在对矩形断面的江心洲分汊研究时,在汊道入口中发现了水流分离区。而对比图3(c)和图4(a)可以发现,两岸滩地近边壁处相对流速较CS03 明显减小,虽还未出现回流,但这已说明在复式分汊河道中,在分流段分离区就已经开始在滩地岸边附近发展。
CS05 断面位于江心洲正前方,水流已经分流,阻水作用对水流流速起到了主导作用,流速在横向上存在显著变化。在主槽中,从支汊一侧到主汊一侧,相对流速从0.7 增大到了1.4,表明在洲头分汊段水流横向运动剧烈。由图4(b)可以看出,支汊进口(y=-0.03 m)由于靠近江心洲且边界约束强,受到的阻水作用更大,垂线流速整体显著减小。支汊近底水流近底流速反向,出现了回流。由于两汊主槽边界的约束差异,在此断面支汊一侧主槽流速受到了极大影响,滩面以下流速显著减小,而滩面以上水流流速受到的阻水作用较小,流速变化不大。
CS06断面已经发展为分汊复式断面,分流作用主导了流速的变化。支汊主槽展宽,流线顺滑,水流与边界的冲击减弱,从图4(c)中可以看出,相对CS05 断面,主槽流速明显增大,近底回流区消失。由于分流流量的差异,两汊主槽流速差异显著。而边界条件的影响在主槽边壁(y=0.70 m)和两汊边滩表现得较为明显。分流水流冲击边壁(y=0.70 m),滩面以下水流流速显著减小,而由于滩面宽阔,水流未受到边壁的约束,滩面以上测点流速仍然维持较高值,因此滩面上下流速差异极大。主汊边壁垂线流速相对于支汊小的多,这表明主汊边壁分离区的发展更快。
CS07断面已经完全发展为分汊断面,江心洲两侧产生了两个方向相反的立轴漩涡[图5(a)为彩沙示踪图],支汊为顺指针,主汊为逆时针。从图5 中可以发现,漩涡中心流速最大,距离漩涡越远,流速逐渐减小。此外,还可以发现两汊断面的不同也导致了流速具有显著差距。
综上所述,在分流段,河道边界的变化和江心洲分流作用是流速变化的主导因素。河道边界的影响表现在两汊主槽边壁的产生的折冲水流,边滩展宽导致的滩地流速减小,以及分离区的发展。两汊分流流量的影响则主要表现在分汊后两汊主槽流速的显著差异。两汊因分流产生的漩涡以及过流量的差异引起的流速差异可能会对江心洲和河道演变产生重要影响。
4 流量对流速的影响
复式河道的滩槽之间存在着水流交换,而两者之间流速不同,将会带来动量的交换。因此,滩槽水流流速必然会相互影响。N G Bhowmilk 和M Demissic[18]曾对美国的两条河流的主槽、河漫滩及全断面的流速随水位变化进行过分析,结果表明水流漫滩以后,随着水位的继续上涨,主槽和全断面的流速反而有所下降。当滩地水深约为主槽平均水深的35%,断面流速达到最低值,自此之后,又随水位的抬高而不断加大。然而,对于最低值之后,流速的变化却未进行深入研究。
如表2所示,在当滩地水深大于主槽平均水深的35%后,随着流量增大,断面流速不断增大,这与前人的研究结果一致。本文试验中,随着流量的梯级增大,支汊一侧滩地流速的增大趋势也增大,而断面平均流速、主槽流速、主汊一侧滩地流速、滩槽水深比的增大趋势则均逐渐减小。这说明在断面流速达最低值后,流速随流量的增大趋势逐渐减缓。而主支汊断面形状的差异导致两汊流速增大趋势的不同,当主汊一侧滩地流速增长变缓时,支汊一侧滩地流速随流量增大仍显著增大。
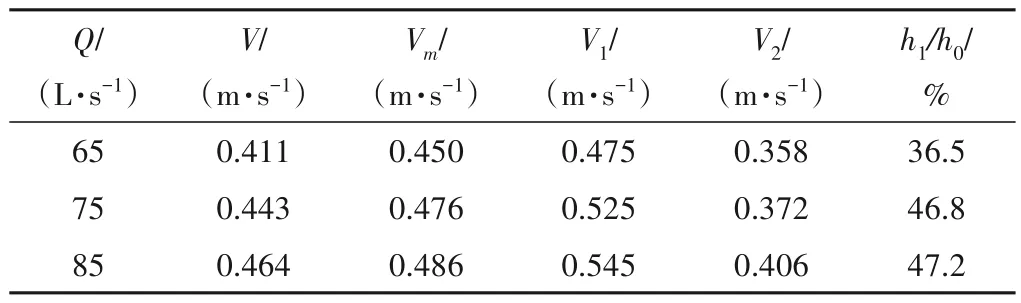
表2 CS04断面流速Tab.2 The velocity in CS04
为反映出分流段流速随流量增大的变化,分析了不同流量下断面CS04 相对流速垂线分布(图6),可以看出,随着流量的增大,主槽相对流速先增大后减小,这表明在35%之后,随着流量的增大,断面流速的增大趋势在某一临界值逐渐减缓。当水位超过一定限度后,滩地的流速增大,不断接近主槽流速,复式断面形态对于水流流速的影响开始不断减弱。这表明,在达到某一阈值后,复式断面形态对断面流速的影响几乎可以忽略。此时,滩槽的区分已经失去了意义,可以将其简化为简单断面河道进行研究。

图6 不同流量下断面CS04相对流速垂线分布Fig.6 Vertical distribution of relative velocity of CS04 under different discharge
5 结 论
通过概化水槽试验,利用相对流速和相对水深两个无量纲数对江心洲洲头分流区流速分布进行了分析,得到如下结论。
(1)在顺直复式分汊河道中,江心洲前的单一复式段的垂线相对流速分布基本满足对数分布。
(2)复式分汊河道洲头的流速主要受分汊形态的影响。随着水流靠近江心洲,江心洲的分流作用与阻水作用先后对流速起到了主导作用,断面平均流速呈现先增大后减小的趋势。此外,由于分汊形态对流速分布具有重要影响,主汊受到江心洲的影响较小,主支汊流速变化程度和趋势有明显不同。
(3)复式断面形态是分汊口主槽和滩地流速变化的主要影响因素。一方面,复式断面形态垂向的变化导致主槽滩面上下水流能量损耗程度出现了差异,滩面上下流速差异显著。另一方面,复式断面形态导致滩地流速产生了横向上的变化。主支汊滩地宽度的不同,也造成了两汊边壁分离区发展的差异性。(4)在当滩地水深大于主槽平均水深的35%后,随着流量增大,断面流速不断增大,断面流速的增大趋势在某一临界值逐渐减缓,复式河道可以简化为简单断面河道来进行研究。

