城市多水源联合供水优化配置研究

郭世浩，殷淑华，姜 彤，刘来胜

（1. 华北水利水电大学地球科学与工程学院，河南 郑州 450046； 2. 中国水利水电科学研究院，北京 100038）

0 引 言

水资源短缺问题已经成为社会经济及全球可持续性的重大问题，其严重威胁人类生存及经济发展。在2019年联合国发表的《世界水发展报告》中提出全球面临水资源短缺问题的人口数约占总人口数的25%，人类正面临全球性的水危机［1，2］。近年来，对稀缺水资源的过度使用和管理不善正在加剧水资源的供需矛盾，导致多用水户用水竞争激烈［2］。因此，通过水资源优化配置，使得有限的水资源可以合理的分配给多目标用水户，对于维护地区和平稳定、促进地区经济可持续发展至关重要［2］。如杜佰林等［3］人构建社会、经济、生态效益为目标的综合评价函数，建立基于模拟退火粒子群算法的优化配置模型，进行求解，与优化前相比具有一定量的节水量；王慧等［4］人基于大系统分解协调原理构建了包含灌区作物种植结构和作物灌溉制度的层次优化模型，并利用NSGA-Ⅱ进行求解，实现了灌区水资源的优化配置；付强等［5］人基于多目标非支配排序的原理建立了农业多水源灌溉多目标优化模型，采用NSGA-Ⅱ进行求解，为当地农业水资源规划与管理提供依据，李欣眙［6］针对白洋淀的生态环境问题，建立基于生态的白洋淀上游水库联合调度模型，采用遗传算法求解及多目标模糊优选模型进行方案寻优，以期实现水资源的合理调配，最终实现白洋淀及其上游河道生态环境的改善。

水资源优化配置通常涉及“水资源—社会经济—生态环境”这一复杂的巨系统，影响因素多，用水目标多，因此在进行水资源优化配置时需要统筹考虑多因素，力求寻找多目标协同配合下的最大综合效益［7，8］。

对于多目标优化配置的求解方法，常用一般有两种:一是将多目标优化问题转化成单目标优化问题进行求解，此方法一次只能求得一个解，效率低下；二是利用启发式智能算法对多目标数学模型进行求解，得到方案解集，通过对解集中方案的筛选得到多目标问题的最优解［9］，一次可以获得多个解，效率高，求解快，受到国内外诸多学者的关注。目前，二代非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm-Ⅱ，NSGA-Ⅱ）已经成为最具代表性的启发式智能算法之一，其采用精英保留策略以及拥挤度计算规则，大大提高运算效率，具有快速非支配排序以及无小生境参数选择的优点，以协调各目标函数间关系为主要目标，在各目标之间寻找最优结果［5，10］。本文针对宁夏东线供水工程及其供水范围进行研究，建立多目标优化数学模型，采用NSGA-Ⅱ算法对模型进行求解，利用多目标模糊优选模型从可行方案中优选出最优方案，为研究区水资源合理利用与分配提供参考依据。

1 银川都市圈水资源优化配置模型构建

1.1 研究区概况

宁夏回族自治区属于干旱、半干旱地区，地处我国西北内陆，近年来，随着城市化、工业化进程不断加快，当地水资源供需矛盾问题日益尖锐，水安全问题日益突出，为此自治区政府提出建设银川都市圈城乡东线供水工程，以解决宁夏银川都市圈黄河以东地区的水资源供需矛盾问题。如图1研究区域供水拓扑结构所示，工程以黄河水为水源，由东干渠进水闸取水后沿管路进入三星塘调蓄水库沉砂，之后进入改造后的金积水厂，经净化处理后分三路分别与青铜峡市（河东）、吴忠市利通区以及灵武市的各个城市地下水水源地，地表水以及中水组成多水源供水格局，为各分区中的居民生活、规模化养殖、工业生产以及生态环境用水户进行供水。研究区域的流域水资源跨越时空较大，涉及到地下水、地表水、跨流域调水工程以及中水回用等多水源，与不同地区不同决策群存在利益关系，是一个多水源多用户的复杂系统［11］，经济、社会和生态环境等用水协调十分困难，因此对其展开水源优化配置研究是十分必要的。

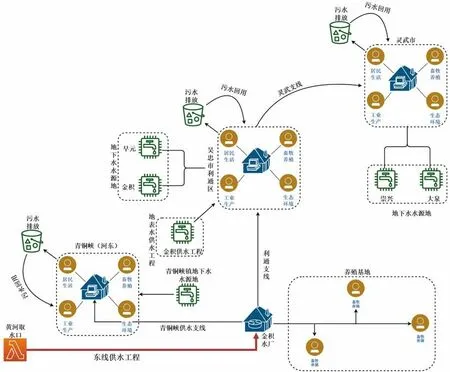
图1 研究区域供水结构拓扑图Fig.1 Topological map of water supply structure in the study area

1.2 决策变量

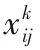
1.3 目标函数

（1）水资源目标:地下水用水量最小。

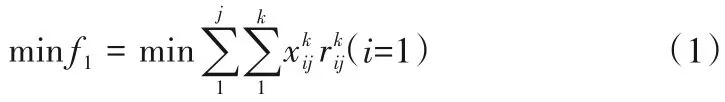
（2）经济目标:净经济效益最大。经济目标往往是决策者重点关注的指标，往往能够很好地展示当地的经济发展现状。以决策变量乘以单位供水产生的经济效益与供水成本之差表述。

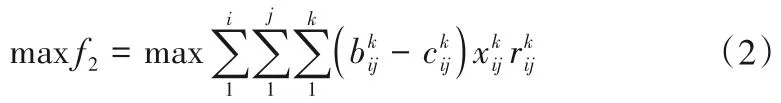
（3）环境目标:污染物COD总排放量最小。

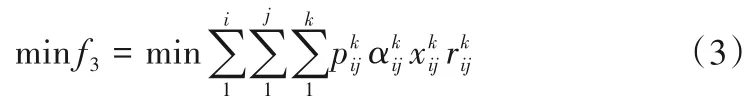
1.4 约束条件

（1）水源供水能力约束。

式中:Wi为i水源的最大可供水量。

（2）用户需水量约束。

式中:Hj为研究区域中j用户的需水量上限；Lj为研究区域中j用户的需水量下限。

（3）变量非负约束。

1.5 参数确定

（1）经济目标系数的确定。各分区工业生产以及规模化养殖费用系数为单位用水量产生的生产总值，城乡居民生活以及生态环境效益系数遵循“保生活、优生态”的原则确定，费用系数可以参考当地水价确定，具体见表1。

表1 2025年各分区各用水户效益系数和费用系数表Tab.1 Table of benefit coefficients and cost coefficients of water users in each district in 2025

（2）环境目标系数的确定。研究区域各分区的污水排放系数依据《银川都市圈城乡东线供水工程可研报告》《银川都市圈东线供水工程水资源论证报告》以及《银川都市圈城乡东线供水工程环评报告书》确定，排放污水中COD 浓度依据《中华人民共和国国家标准-污水综合排放标准》确定，其中城乡居民生活与工业生产污水排放率分别为0.45%、0.38%；规模化养殖与生态绿化不排放污水，城乡居民生活与工业生产排放污水中COD排放浓度分别为60、100 mg/L。

（3）供需水预测。科学合理的水资源优化配置方案是以严谨的水资源供需平衡分析为基础的［12］。研究区域水资源优化配置的需水端包括城乡居民生活、工业生产、规模化养殖以及生态环境等，供水端包括地表水、浅层地下水、以及中水回用等。在对研究区域各分区《国民经济和社会发展报告》《银川都市圈城乡东线供水工程可研报告》《银川都市圈东线供水工程水资源论证报告》以及《银川都市圈城乡东线供水工程环评报告书》等资料分析的基础上进行供需水预测，结果见表2与表3。

表2 2025年研究区域需水量上下限预测成果表 万m3Tab.2 Prediction results of the upper and lower limits of water demand in the study area in 2025

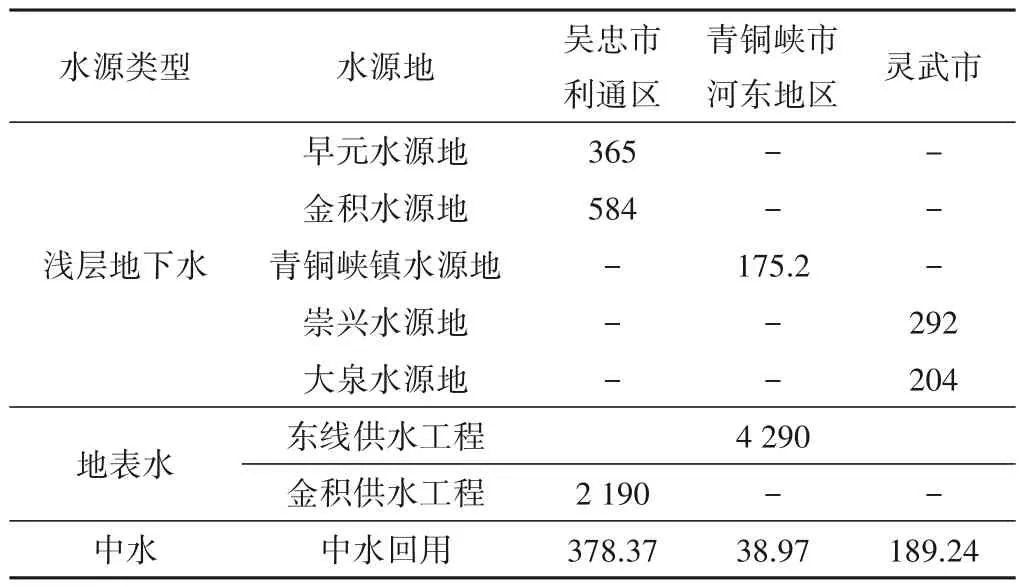
表3 2025年研究区域各水源可供水量预测成果表 万m3Tab.3 Prediction results of water availability for each water source in the study area in 2025

通过对过往3～5 a 的人口平均自然增长率进行统计以及对未来综合增长率进行预测，以2020 年为基准年，对研究区域2025年人口以及经济发展进行预测，采用定额法对研究区域各用户（城乡居民生活、工业生产、规模化养殖以及生态环境）进行需水量分析预测以及对各分区所有可供水水源进行供水量分析预测，结果见表2和表3。

2 模型求解与方案优选

2.1 模型求解

多水源城市供水优化调度是一个多目标、多变量和多约束的复杂问题，往往需要考虑系统特殊规则的处理、多目标均衡解的选择以及求解算法的普适性［13］。

1997 年，Srinivas［14］首 次 提 出 非 支 配 排 序 遗 传 算 法（NSGA），由于NSGA 有易早熟以及计算复杂度高的缺点，Deb等人［15］于2002 年在NSGA 的基础上开发二代版本NSGA-II，其通过基于帕累托优势概念的精英保留策略和基于拥挤距离的二次选择方法，采用快速非支配排序方法对父代与子代种群进行排序，降低了求解复杂度，使其能够更加迅速地找到最优解。主要用于解决单目标或者多目标优化问题，被公认为行业标准算法之一，被广泛应用于许多科学领域，包括工程、经济、物流和水资源调度等，在这些领域中，往往需要在多个相互冲突的目标之间进行权衡后做出最佳选择［16，17］。使用这两种选择方法可以显著提高其解决复杂多目标问题的性能，求解原理见图2［17］。本文在建立多目标数学优化模型后采用NSGA-II 对模型进行求解。

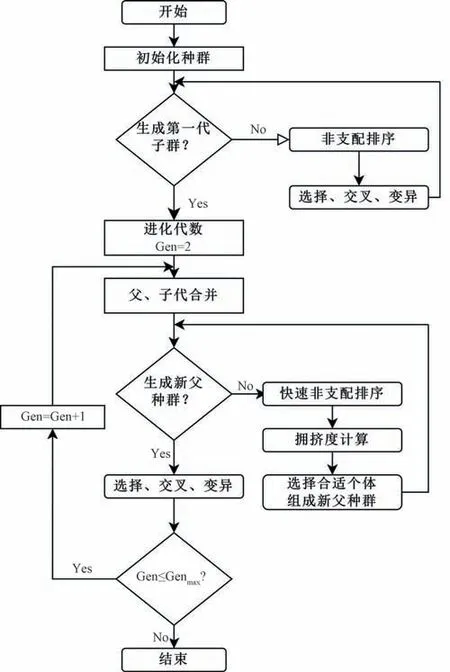
图2 NSGA-Ⅱ原理图Fig.2 Schematic diagram of NSGA-II

2.2 多目标模糊优选模型

水资源优化配置属于多目标优化决策问题，通过NSGA-II对多目标问题进行求解，产生n个Pareto 非劣解，分别对应n个优化调度方案，从n个优化调度方案中筛选出最优方案。由于方案筛选时存在相对性和模糊性［6］，基于陈守煜［18］教授提出“系统模糊优选模型”，将其简化为单层次模糊优选模型，利用各方案的目标特征值计算出各方案中各目标的隶属度，得到模糊关系矩阵，在确定各目标权重后通过式（14）计算出各方案的相对优属度，对不同配置方案进一步优化筛选。

将多目标优化数学模型求解得到的Pareto解集组成方案集P，形成目标特征值矩阵:

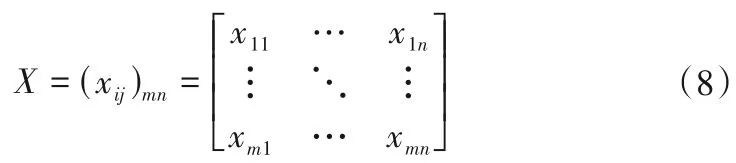
式中:m为调度方案的数量（与采用NAGA-II 求解过程中的种群大小一致）；n为评价指标的数量；xij为第i种方案j目标的特征值。

由于目标特征值转化为相应的隶属度，通常可分为两种形式:越大越优型，越小越优型，计算方法如下:

越大越优型:

越小越优型:

式中:ri j为i方案中j目标的相对隶属度，取值范围为0～1，越接近1 说明隶属度越高；xmaxj为方案集中j目标的最大特征值；xminj为方案集中j目标的最小特征值。

通过上述计算得到目标模糊关系矩阵R:

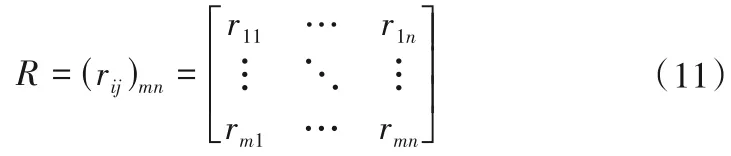
采用模糊算子M（∧，∨）取模糊关系矩阵中的最小值rb与最大值rg，分别为理想劣方案与理想优方案，其关系如下:

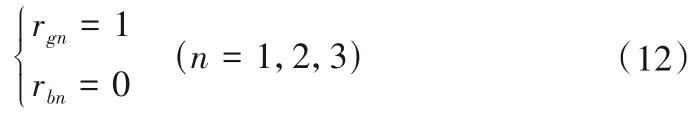
假设方案中的n个目标具有不同的权重，则权重向量W表述为:

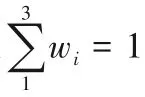
则各个方案相对优属度可由公式（14）计算得到，选择相对优属度大的方案作为最优方案:

3 结果分析

3.1 Pareto解集

利用NSGA-II 对建立的水资源多目标优化模型进行求解，将初始种群数设为200，通过设置不同的迭代次数（100、200、400、700、1 000），分析不同迭代次数的收敛情况，迭代100 次、200 次、400 次、700 次和1 000 次求得的Pareto 非劣解集如图3所示。由图3 可以看出，不同的迭代次数Pareto 非劣解集收敛性与分布性不尽相同，通过对超体积指标（HyperVolume indicatior，HV）计算来评判Pareto 非劣解集收敛性与分布性，HV计算过程中不需要真实的Pareto前沿，只需要确定一参考点，计算参考点与Pareto 非劣解集中各个点所形成的超立方体的体积，HV值越大，Pareto 解集收敛性与分布性表现越好，计算公式如下所示［19］:

图3 不同迭代次数Pareto前沿面图集Fig.3 Atlas of Pareto frontiers with different iterations

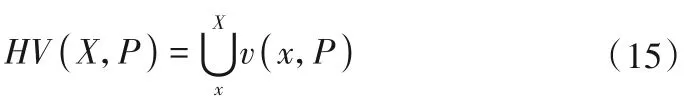
式中:X为已知Pareto 非劣解集；x为已知Pareto 非劣解集中的点；P为参考点。

HV计算不需要真实Pareto 解集，只需要设置参考点，但对于如何在给定问题的基础上选用最佳参考点尚未有具体定论，根据Ye Tian［20］等人的介绍，HV计算过程中所选参考点为反最佳点，因此本文在计算HV指标过程中所选参考点为迭代过程中各目标的最大值。

HV计算结果如图4所示，随着迭代次数增加，参数HV的值在不断增大，迭代100，200，400，700，1 000 次的HV值分别为0.563 0，0.644 3，0.666 9，0.682 3，0.688 0，计算时间分别为15.64，32.15，60.98，108.36，151.52 s，说明随着迭代次数的不断增加，计算时间不断增长，Pareto 解集前沿面的收敛性和分布性越来越好。由图3 可以看出随着迭代次数的增加，XY面上的投影点逐渐密集收敛，同样的在XZ以及YZ面上，数据点的密集程度随着迭代次数的增加也有不同的改变，特别是在100 次到700 次迭代过程中，可以明显的看出各个投影面上的点密集程度有所不同，相应的HV值也在此区间范围内变化幅度较大。随着700次迭代后HV值的逐渐稳定，说明700次后产生的Pareto解集前沿面的收敛性与分布性无明显差异，因此，在综合考虑计算时间以及收敛性与分布性情况，确定700 次迭代次数获得的Pareto解集作为后续数据分析计算的基础。

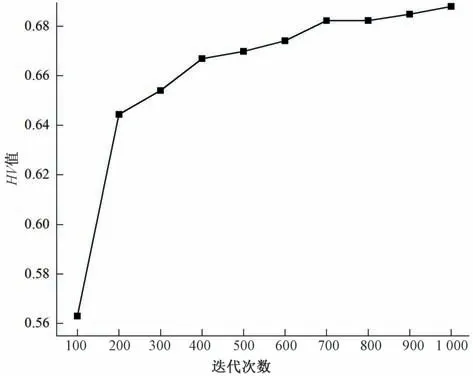
图4 不同迭代次数HV值变化趋势示意图Fig.4 Schematic diagram of the change trend of HV value with different iteration times

3.2 多目标间相关关系分析

本文多目标数学优化模型的3 个目标中，水资源目标与环境目标为越小越优型，经济目标为越大越优型，各目标的最优最劣解见表4。

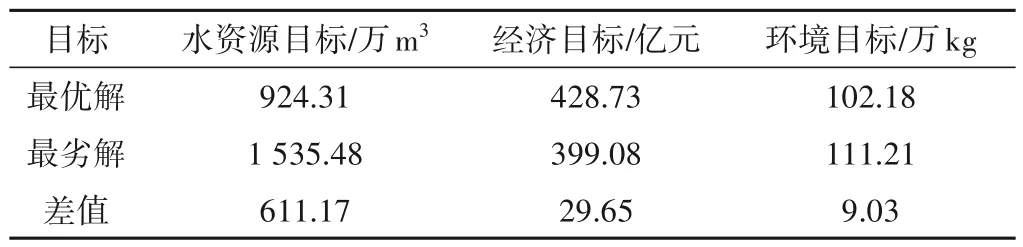
表4 各目标优劣解情况Tab.4 Pros and cons of solutions for each target

将各目标的最大隶属度定义为1，最小隶属度定义为0，通过前述节2.2 多目标模糊优选模型确定的方法计算各目标的相对优属度，如图5所示。

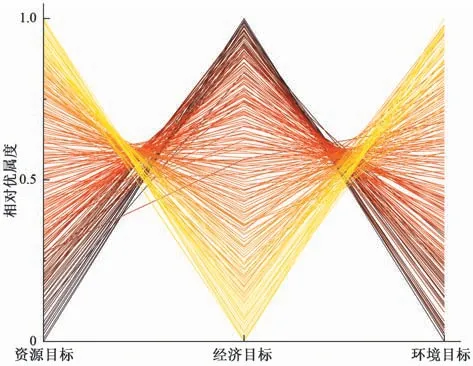
图5 多目标Pareto解集相对隶属度Fig.5 Relative membership of multi-objective Pareto solution set

图5 中不同颜色线条代表不同方案3 个目标的相对隶属度关系，当一个目标相对隶属度为1时，其他两个目标相对隶属度无法全部为1，说明本文建立的数学优化模型的3 个目标之间存在相互竞争、相互矛盾的关系，3个目标不可能同时达到最优解；在水资源目标相对隶属度较高时经济目标隶属度较低，两者之间存在相反趋势，说明两者之间存在一定的竞争关系；同理经济目标相对隶属度处于较高水平时环境目标隶属度较低，说明两者之间同样存在一定的竞争关系；相反，环境目标隶属度在水资源目标隶属度较高时依然保持着较高水平，说明两者之间存在着一定的协同关系。

为了更准确地体现水资源目标、经济目标与环境目标间的相关关系，将各目标进行两两关系作图，结果如图6 所示，图6（b）为水资源目标与经济目标之间相关关系图，由图6可以看出随着水资源目标地下水用水量的不断缩减，数值左移，不但经济效益在呈下降趋势，而且污染物排放量也在减少，这是因为地区经济效益的发展需要水资源的支撑，经济发展缓慢使得污染物排放量也在不断的减少；图6（c）为经济目标与环境目标之间相关关系图，由图6 可以看出在经济不断增长的过程中环境中重要污染物COD 的排放量也在增加，呈正相关趋势，说明经济的发展势必会带来一系列的环境问题；图6（d）所示为环境目标与水资源目标间的相关关系，由图可以看出随着地下水用水量的不断增加，污染物排放量也在不断的增长，说明供水量的增加会引起污染物排放量的增大。综上所述，随着地下水用水量的不断缩减，地区经济效益受到较大影响，但是却使得环境目标向好发展，污染物排放量减少。

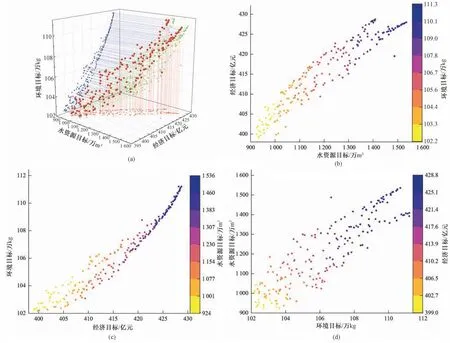
图6 水资源目标、经济目标与环境目标间相关关系图Fig.6 Correlation diagram between resource goals， economic goals and environmental goals

3.3 方案优选

3.3.1 目标权重确定

采用多目标模糊优选模型对结果进行筛选过程中目标权重W的确定起着至关重要的作用，在一些常规的模型中，往往根据人的主观判断来确定目标权重，使得权重应用含义不明，参考意义不大，二元比较法［6，21-23］可以将人的经验通过数学模型的形式展示出来，通过确定合理的目标权重并融入多目标模糊优选模型中，以此来筛选模型最优方案，使得多目标综合效益达到最优，计算过程如下［8］:

（1）按照重要程度排序:水资源目标＞经济目标＞环境目标；

（2）重要程度对比:将水资源目标与其他两个目标进行重要程度对比，可使用模糊语气程度:同等重要、略为重要、明显重要、十分重要、极其重要、无可比拟表述，令同等重要ui=0.5，随着模糊语气的加强，相互比较的程度也是逐步加强的，直至无可比拟uI=1.0，其他语气的重要度可按0.5～1.0 间的变化根据线性内插求得，本文水资源目标比经济目标略为重要，水资源目标比环境目标明显重要，故各目标模糊语气程度为（u1，u2，u3）=（0.5，0.6，0.7）；

（3）计算各目标重要度:

（4）归一化处理:

式中:j为目标函数个数，取1，2，3。

通过二元比较法确定的水资源目标、经济目标与环境目标的重要度Wj'分别为1，0.67，0.43，归一化处理后各目标权重Wj为0.48、0.32、0.2。

3.3.2 最优目标方案值

按照上述二元比较法确定的目标权重以节2中公式（14）计算得相对优属度ui，挑选出相对优属度最大的方案作为此权重下的最优方案，其目标值见表5。

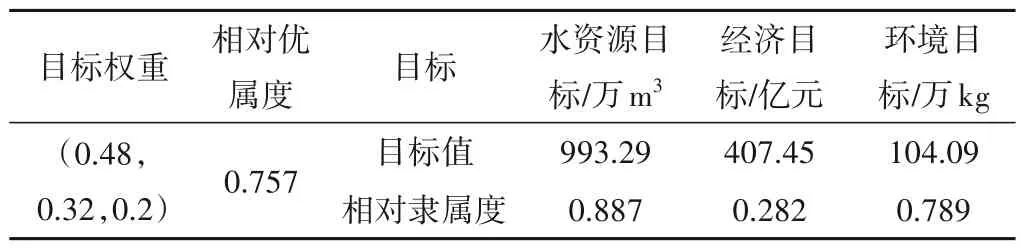
表5 最优方案目标值Tab.5 Target value of optimal plan

3.3.3 最优配水方案

按照最大相对优属度原则找到方案集中的最优解，对应最优配水方案见表6，其中缺水率计算公式为:

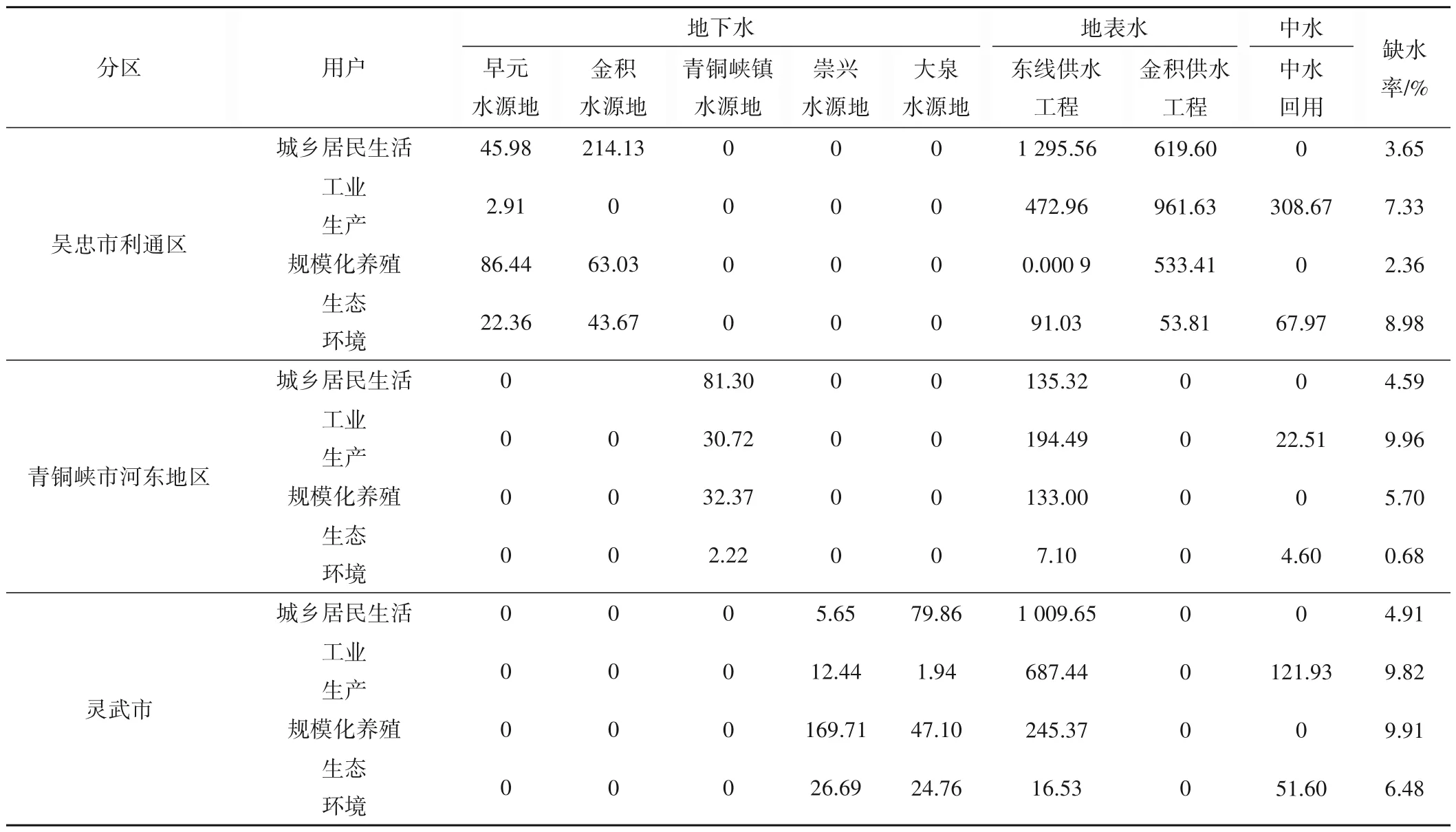
表6 研究区域各分区水源分配方案表 万m3Tab.6 Water source allocation plan for each subregion of the study area

式中:需水量为表2 中需水量上限值；供水量为各水源供水量之和。

如表6所示，吴忠市利通区、青铜峡市河东地区以及灵武市的城乡居民生活缺水率分别为3.65%、4.59%、4.91%，缺水率控制在5%之内；工业生产缺水率分别为7.33%、9.96%、9.82%，缺水率控制在10% 以内；规模化养殖缺水率分别为2.36%、5.70%、9.91%，缺水率控制在10%以内；生态环境缺水率分别为8.98%、0.68%、6.48%，缺水率控制在10%以内，所有缺水率符合各用水户需水下限要求；此配置方案下目标函数值地下水用水量为993.29 万m3、地表水用水量为6 456.90 万m3、经济目标为407.45 亿元、环境目标为104.09 万kg。通过合理的水资源优化配置，在地下水用水量尽量小的情况下统筹考虑经济与环境目标，在提高了当地的经济发展的同时使得COD 总排放量减小，为研究区域管理决策者进行水资源分配时提供方案参考。

4 结 论

（1）通过建立水资源、经济和环境的多目标数学优化模型，采用NSGA-Ⅱ对其进行求解，得到符合约束条件的Pareto 解集；在综合考虑计算时间以及收敛性与分布性情况，确定700次迭代次数获得的Pareto解集作为后续数据分析计算的基础；

（2）通过对方案集中各目标值的模糊隶属度进行计算，分析目标间相关关系得出水资源目标与经济目标以及经济目标与环境目标间呈负相关关系，水资源目标与环境目标间呈正相关关系；

（3）综合考虑水资源目标、经济目标、环境目标，采用二元分析法确定各目标权重为0.48、0.32、0.2，通过多目标的相对优属度ui计算，挑选相对优属度ui值最大为最优方案，可以实现水资源优化配置，在最优方案下地下水用水量为993.29 万m3、地表水用水量为6 456.90 万m3、经济目标为407.45 亿元、环境目标为104.09 万kg。