基于矩形单元波函数叠加法的平面近场声全息

范少杰 向宇 石梓玉

摘 要：波叠加法和等效源法都是平面近场声全息中的常用方法。传统波叠加法需要对所有单元计算数值积分，效率较低；等效源法直接将单元积分简化为单极子点源，计算效率获得提高，但其过度简化导致精度损失。针对以上问题，在基于波叠加法的平面近场声全息基础上，提出一种替代矩形单元积分的波函数叠加法。该方法将矩形单元的积分声场表示成Helmholtz方程球面波谱的波函数形式，并结合球面波谱的性质，将单元的远场球面波谱内推至近场，由此获得了与矩形单元积分声场等价的外部声场显式波函数解析表达式，有效避免了传统波叠加法的数值积分以及传统等效源法的过度简化。利用矩形简支板的近场声全息算例对比了所提方法、传统波叠加法以及传统等效源法的重建效果。结果表明：所提方法在全频段的声场重建精度均高于传统等效源法，在高频段的重建精度高于传统波叠加法，其计算效率显著高于传统波叠加法。

关键词：近场声全息；波叠加法；等效源法；波函数

中图分类号：TB52 DOI：10.16375/j.cnki.cn45-1395/t.2023.02.001

0 引言

近场声全息是噪声检测与声源识别定位中的常用技术，该技术最早由Williams等[1]在20世纪80年代应用于声学计算领域。经过各国学者数十年研究，由最初的基于空間傅里叶变换算法（SFT）的近场声全息技术[2]发展出了更多适用范围更广的近场声全息算法[3]。为了克服空间傅里叶变换算法只能适用于规则形状声源的局限性，Veronesi等[4]在1989年将边界元法引入声场近场声全息技术中。Bai[5]对该方法进行了改进，随后被大量应用于工程实践中[6-7]。虽然边界元法适用于任意形状的声源，但其复杂的奇异积分处理也相应地提高了计算成本。Koopmann等[8]于1989年将波叠加的思想应用到声场计算中，通过在辐射体内部布置虚拟源来模拟声源外部声场。由于虚拟源与真实边界不重合，从而避免了边界元法中的奇异积分，进一步提高了计算效率。

在实际工程及试验测量中，平面传声器阵列布置相对简单，被广泛应用于声源近场的声场重建中[9-10]。在基于传统波叠加法的平面近场声全息中，需要计算虚拟边界上离散单元的数值积分，其精度较高，但单元积分运算将耗费大量时间成本。若将单元积分简化为单极子点源，则得到传统的单极子等效源法。该方法无需计算单元积分，计算效率得到很大提高[11]，但从单元积分简化为点源的过程中，由于存在较大的边界离散误差和积分近似误差[12-13]，其计算精度低于波叠加法。

为提高传统波叠加法的计算效率并兼顾其计算精度，本文以工程中常用的矩形单元为例，提出了一种利用具有显式解析表达式的波函数代替单元积分的方法。文中详细阐述了波函数的推导过程，并简要分析了波函数的性质，最后利用简支板的算例对比了所提方法与传统方法在声场重建中的效果。

1 基于波叠加法的平面近场声全息原理

在基于波叠加法的平面近场声全息中，通常在求解域之外的虚拟边界上布置虚拟源来模拟真实声源产生的声场，如图1所示。

对于常用矩形采样阵列，为了保证波叠加法的计算精度以及稳定性，一般设置虚拟面与全息面共形，如图1（a）所示，其声压可由式（1）表示：

[pr=SEq（rE）G（r，rE）dSE（rE）]. （1）

其中：[r]为场点位置矢量；[SE]为与全息面共形的矩形虚拟边界；[q（rE）]为虚拟源的源强；[rE]为虚拟边界上虚拟源位置矢量；[G（r，rE）]为自由场格林函数。若将虚拟边界离散成[N]个大小形状均相同的矩形常数单元，如图1（b）所示，则式（1）可写为：

[pr=i=1Nqi0Lx0LyG（r，rE）dSEi（rE） ，i=1，2，…，N]. （2）

式（2）即为传统波叠加法的声压计算公式，其中，[qi]为第[i]个单元的虚拟源强；[Lx]和[Ly]分别为离散单元的边长；[SEi]为第[i]个离散单元。

由式（2）可以看出，计算任意场点的声压时，需要对每个单元进行积分计算，因此，使用传统波叠加法来计算声场的效率很低。为了解决传统波叠加法计算效率的问题，通常采用虚拟点源代替单元积分的方法来计算声场[14-15]。如图1（c）所示，若在虚拟边界上布置[N]个单极子虚拟点源，则任意场点的声压可由该[N]个单极子点源所产生的声场叠加表示[16]：

[pr=i=1NqiG（r，rEi）][， ][i=1，2，…，N]. （3）

式（3）即为单极子等效源法，其中，[rEi]为第[i]个等效源的位置。利用声源近场区域的全息面测得声压数据，并代入式（2）或式（3），求出虚拟源强[17]：

[q=G-1HEpH]. （4）

其中：[q]为虚拟源强列向量；[G-1HE]为全息测点与虚拟源间的传递矩阵逆矩阵；[pH]为全息测点声压数据列向量。求出虚拟源的源强之后，再代入式（2）或式（3）即可获得重建面上场点声压，这便是基于波叠加法的近场声全息原理。

通过上述对基于波叠加法近场声全息原理的分析可以看出，传统波叠加法从波叠加方程导出，理论上计算精度更高，但是存在计算效率低的问题。单极子等效源法是对传统波叠加法的简化算法，该方法不需要单元插值处理和积分运算，计算效率高，在位置和数量合适的情况下可以达到较高的精度[18]。然而从传统波叠加法到单极子等效源法的近似过程中存在着一定的积分误差，这些误差一定程度上影响着单极子等效源法的计算精度。为兼顾波叠加法的计算精度和单极子等效源法的计算效率，本文提出一种波函数方法。

2 波函数的构造

对于图1的离散模型，每一个离散的矩形单元大小形状均相同，因而其声场必然都是相同的。对此，任取一个单元，并以单元的形心[O]为原点，建立坐标系[Oxyz]，其[x]轴和[y]轴分别平行于单元的长和宽，如图2所示。

由式（2）可知，相对于该单元中心的场点[r]在单元下的积分形式为：

[p（r）=-Lx2Lx2-Ly2Ly2G（r，r）dxdy. ] （5）

式中，[r]是单元上的点的坐标矢量。若能将式中的积分形式表示成波函数[W（r，θ，φ）]的形式：

[p（r）=W（r，θ，φ）]. （6）

则可以在计算任意场点的声场时，只需把其相对坐标[r、θ、φ]代入波函数[W（r，θ，φ）]即可，从而避免积分。由球面波辐射理论[2]可知，在声源的外域，声压满足球面坐标系下Helmholtz方程的解，从而式（6）可用球面波展开：

[pr=n=0∞ m=-nnPmnrYmnθ，φ]. （7）

式中：[Pmn（r）]是半径为[r]的球面上的第[（n，m）]阶声压球面波谱；[Ymnθ，φ]为归一化球谐函数。

[Ymnθ，φ=2n+14πn-m！n+m！Pmncosθeimφ]. （8）

其中：[Pmncosθ]为连带勒让德函数，i=[-1]。由式（7）可知，只要求出球面波谱[Pmn（r）]即可获得[p（r）]的解。

由球面波谱理论可知，球面波谱[Pmn（r）]可通过已知半径为[R]的球面波谱[Pmn（R）]来求解：

[Pmn（r）= h（2）n（kr）h（2）n（kR）Pmn（R）]. （9）

式中，[h（2）n]（*）表示第二类球[Hankel]函数，其中，球面波谱[Pmn（R）]可利用球谐函数的完备正交性进行求解[19]：

[Pmn（R）= 02π0πpRYmnθ，φsinθdθdφ]. （10）

式中：[pR]为该单元在半径[R]的球面边界上的声压分布；[Ymnθ，φ]是[Ymnθ，φ]的复共轭。因此，只要确定了[pR]，即可由式（10）求得球面波谱[Pmn（R）]。对于矩形常数单元，一般有2种确定[pR]的方法，一种方法是采用式（5）计算：

[p（R）=-Lx2Lx2-Ly2Ly2G（R，r）dxdy.] （11）

该方法适用于计算任意半径球面边界的声压，但需要计算数值积分。将式（11）获得的[pR]代入式（10）可得到任意半径[R]球面的球面波谱[Pmn（R）]：

[Pmn（R）=][-Lx2Lx2-Ly2Ly202π0πG（R，r）Ymn（θ，φ）sinθdθdφdxdy.]

（12）

另一种方法是直接采用格林函数的远场近似表达式获得 [20]：

[pRF= LxLyexp-ikRF4πRFsinckxLx2sinckyLy2].

（13）

式中：[kx= ksinθcosφ]，[ky= ksinθsinφ]，i=[-1]。该方法适用于计算半径[RF]远大于单元尺寸的远场球面边界的声压。将获得的[pRF]代入式（10）可得到远场球面波谱[Pmn（RF）]：

[Pmn（RF）=02π0π LxLyexp（-ikRF）4πRFsinckxLx2]·

[sinckyLy2Ymnθ，φsinθdθdφ]. （14）

式中，[sinc?=sin?/?]。可以看出，计算任意球面边界的球面波谱[Pmn（R）]需要四重积分，而计算远场球面边界的球面波谱[Pmn（RF）]仅需要二重积分，求解效率更高。因此，本文均采用远场球面波谱[Pmn（RF）]来构造波函数。将式（7）、式（9）、式（14）联立得单元的波函数：

[Wr，θ，φ=n=0∞m=-nnh（2）nkrh（2）nkRFPmn（RF）Ymnθ，φ]. （15）

于是，任意场点的声压可由[N]个单元的波函数叠加求得：

[p（r）=i=1NqiWri，θi，φi ， i=1，2，…，N]. （16）

其中：[qi]为第[i]个波函数的源强；[ri、θi、φi]分别为场点相对于第[i]单元的相对坐标值。

3 数值仿真

在采用波函数进行计算时，必须先确定截断项数。理论上来说，选取的阶数越多，波函数越逼近精确的积分声场，但项数过多会导致计算效率降低。经大量试算发现，仅需取[n=2]，就可以保证波函数具有较好的计算效果。而且由于矩形声源的对称特性，只有当[n]和[m]均为偶数时，球面波谱为非零解，即仅需求解[4]个球面波谱：[P0，0RF]、[P0，2RF]、[P-2，2RF]、[P2，2RF]。下文的算例均采用该参数进行计算。

在实际工程中，连续分布的结构振动声源较为常见，如板、壳等结构振动产生的声场。因此，本算例采用受间歇激励作用的四周无限大矩形简支板声源来比较波函数法、单极子等效源法和传统波叠加法的声场重建效果，仿真模型如图3所示。全息面、重点面、虚拟面及声源的相对位置如图3（a）所示，矩形简支板为铝板，其长宽为[0.5 m×0.5 m]，厚度为[0.002 m]，杨氏模量[E=7.1×1010 Pa]，泊松比[υ=0.33]，密度为[2.7×103 kg/m3]。简支板位于[Z=0]处的[XY]平面上，對简支板施加幅值为[1 N]的中心激励，激励点位置为[（0.25，0.25，0）]；全息面大小与简支板相同，位于简支板上方[0.05 m]，长宽方向均按[0.025 m]间隔划分共计[21×21]个测点；重建面位于简支板上方[0.03 m]处，由于该矩形简支板为中心激励的正方形简支板，其产生的声场有中心对称的特点，因此在重建面上分别选取A（0.25，0.25，0.03）、B（0.35，0.35，0.03）、C（0.45，0.45，0.03）、D（0.25，0.45，0.03）、E（0.35，0.25，0.03）等5个点作为重建点，如图3（b）所示。虚拟面单元划分方式与全息面相同，共计[20×20]个大小相同的正方形虚拟单元，并将其设置在重建面下方[1]倍虚拟单元距离处，等效源点取为各单元的中心点。全息面和重建点的解析复声压和振速值由瑞利积分获得 [21]。分别用3种方法重建5个点处的声压与振速，重建频率范围设置为[f∈［100，4 500］] Hz，重建频率间隔设置为[10 Hz]，重建误差（[δ]）由式（17）计算：

[δ= E-ErE×100% ]. （17）

其中：[E]为解析值，[Er]为重建值。

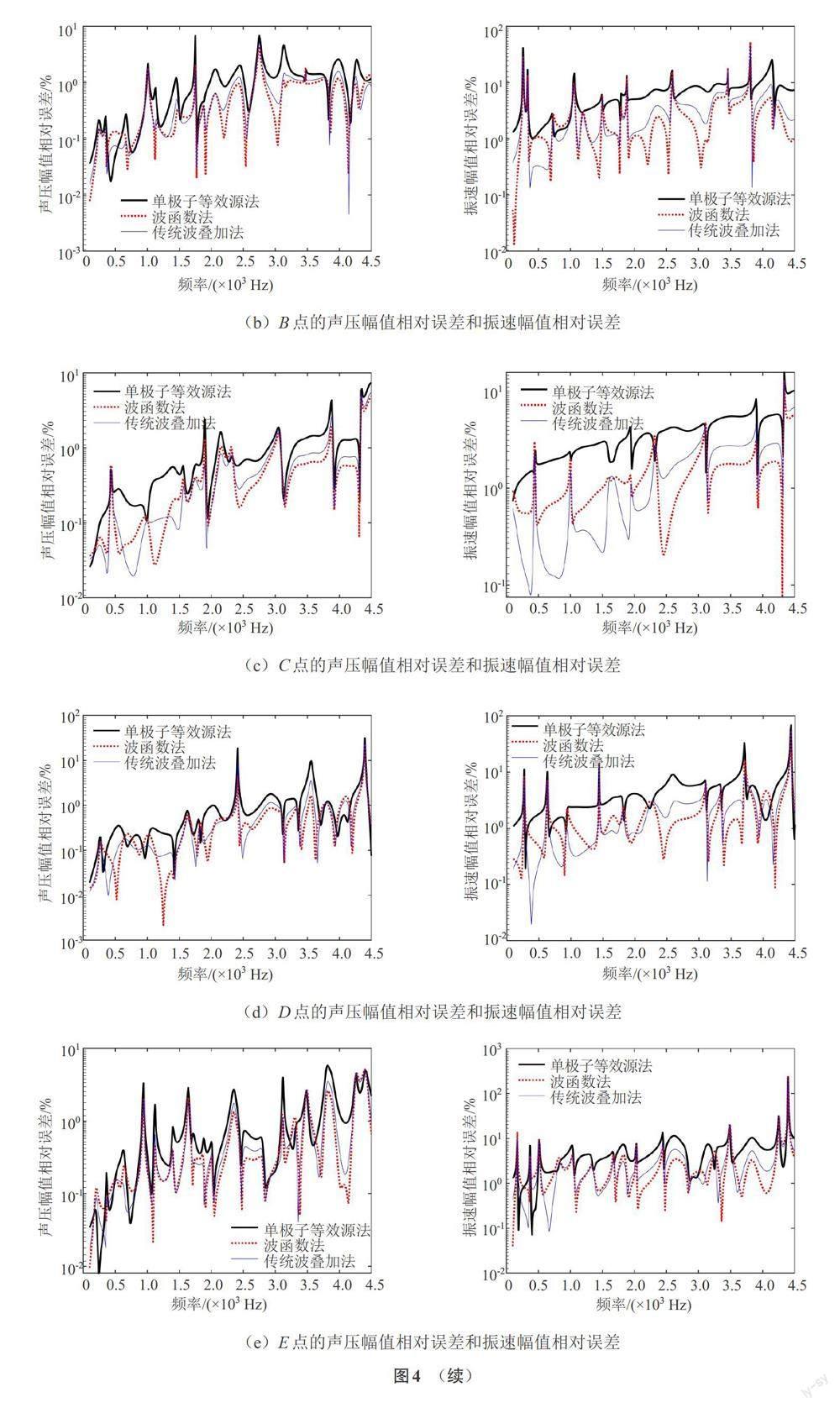
图4显示了3种方法重建[5]个场点处的声压和振速幅值的相对误差。可以看出，对于不同位置的重建点，波函数法和传统波叠加法的总体重建效果（尤其是振速）均优于单极子等效源法。其中，当重建点位于重建面中心时，波函数法和传统波叠加法的重建误差略低于单极子等效源法；当重建点逐渐远离中心时，波函数法和传统波叠加法的重建误差明显低于单极子等效源法；在低频段，波函数法的声压重建精度与传统波叠加法相当，振速重建精度略低于传统波叠加法；但在中高频段，波函数法的声压和振速重建效果甚至优于传统波叠加法。这是由于本文在采用波叠加法时，仅采用了[4×4]点的高斯勒让德积分，对于低频，这些积分点是足够的，所以其精度很高，但随着频率的升高，积分数量的不足导致波叠加法的精度有所下降。但本文方法由显示解析表达式构成，并不受限于单元积分点的数量，因此在高频具有一定的优势。

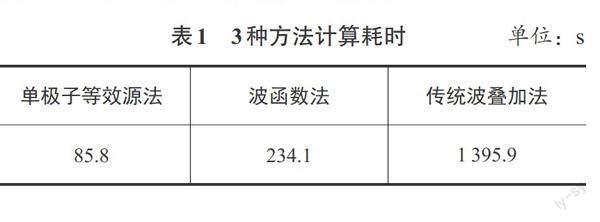
表1中记录了该算例中3种方法所消耗的时间。可以发现，形式最为简单的等效源法在所有方法中的耗时最短，其计算时间仅为波叠加法的1/16。波函数法的计算时间虽长于等效源法，但由于无需数值积分，因而其计算时间仅为波叠加法的1/6。综合考虑计算精度与计算效率，波函数方法相较于等效源法和波叠加法均具有一定优势。

4 结论

针对传统波叠加法数值积分计算效率低和单极子等效源法过度简化的问题，提出了一种波函数代替积分的方法，该方法兼顾了传统波叠加法的计算精度和单极子等效源法的计算效率。文中对所提方法进行了详细推导和阐述，并通过数值仿真进行了验证。计算结果表明：本文方法在全频段的计算精度，尤其是振速的计算精度均高于单极子等效源法，在高频段的计算精度高于波叠加法，计算效率远高于波叠加法。目前本文方法仅应用于平面近场声全息中，对于其在任意形状近场声全息中的应用，有待进一步深入研究。

参考文献

[1] WILLIAMS E G，MAYNARD J D. Holographic imaging without the wavelength resolution limit[J]. Physical Review Letters，1980，45（7）：554-557.

[2] WILLIAMS E G. Fourier acoustics：sound radiation and nearfield acoustical holography[M]. Pittsburgh：Academic Press，1999.

[3] 陈心昭，毕传兴. 近场声全息技术及其应用[M]. 北京：科学出版社，2013.

[4] VERONESI W A，MAYNARD J D. Digital holographic reconstruction of sources with arbitrarily shaped surfaces[J]. Journal of the Acoustical Society of America，1989，85（2）：588-598.

[5] BAI M R. Application of BEM （boundary element method） based acoustic holography to radiation analysis of sound sources with arbitrarily shaped geometries[J]. Journal of the Acoustical Society of America，1992，92（1）：533.

[6] 吳飞，余神志，刘苏行，等. 车用制动空气压缩机结构辐射噪声特性研究[J]. 声学技术，2021，40（2）：228-233.

[7] 张建民，安俊英. 深海波导中目标低频声散射特性研究[J]. 声学技术，2022，41（3）：419-425.

[8] KOOPMANN G H，SONG L，FAHNLINE J B. A method for computing acoustic fields based on the principle of wave superposition[J]. Journal of the Acoustical Society of America，1989，86（6）：2433-2438.

[9] 张永斌，毕传兴，陈剑，等. 基于等效源法的平面近场声全息及其实验研究[J]. 声学学报，2007，32（6）：489-496.

[10] 陈汉涛，郭文勇，韩江桂，等. 船舶机舱内高频弱声源近场声全息方法[J]. 舰船科学技术，2019，41（21）：138-143，147.

[11] CHELLIAH K，RAMAN G，MUEHLEISEN R T. An experimental comparison of various methods of nearfield acoustic holography[J]. Journal of Sound and Vibration，2017，403：21-37.

[12] VALDIVIA N P，WILLIAMS E G. Study of the comparison of the methods of equivalent sources and boundary element methods for near-field acoustic holography[J]. Journal of the Acoustical Society of America，2006，120（6）：3694-3705.

[13] VALDIVIA N P. Advanced equivalent source methodologies for near-field acoustic holography[J]. Journal of Sound and Vibration，2019，438：66-82.

[14] 石梓玉，向宇，陆静，等. 一种提高声场重构稳定性的射线等效源法[J]. 广西科技大学学报，2019，30（3）：1-7，21.

[15] 陈岩豪，向宇，石梓玉. 基于波叠加近场声全息射线波函数的信息补偿[J]. 广西科技大学学报，2021，32（3）：6-12.

[16] WU S W，XIANG Y. Location optimization of monopole equivalent sources in wave superposition method[J]. International Journal of Acoustics and Vibrations，2018，23（2）：254-263.

[17] 张阳，向宇，石梓玉. 二维声全息的δ函数约束型射线波叠加法[J]. 广西科技大学学报，2020，31（4）：19-26，48.

[18] BAI M R，CHEN C C，LIN J H. On optimal retreat distance for the equivalent source method-based nearfield acoustical holography[J]. Journal of the Acoustical Society of America，2011，129（3）：1407-1416.

[19] 丁丹丹. 基于球形阵的封闭空间噪声源定位[D]. 哈尔滨：哈尔滨工程大学，2017.

[20] 王斌，汤渭霖，范军. 一种辐射声场近似计算方法：单元辐射叠加法[J]. 声学学报，2008，33（3）：226-230.

[21] WILLIAMS E G，MAYNARD J D. Numerical evaluation of the Rayleigh integral for planar radiators using the FFT[J]. Journal of the Acoustical Society of America，1982，72（6）：2020-2030.

Planar near-field acoustic holography based on rectangular element wave function superposition method

FAN Shaojie1，2， XIANG Yu*2， SHI Ziyu2

（1. School of Mechanical and Automotive Engineering， Guangxi University of Science and Technology， Liuzhou 545616， China; 2. Guangxi Key Laboratory of Automobile Component and Vehicle Technology

（Guangxi University of Science and Technology）， Liuzhou 545616， China）

Abstract： Both wave superposition and equivalent source methods are commonly used in planar near-field acoustic holography. The conventional wave superposition method needs to calculate numerical integration for all elements， which is less efficient; the equivalent source method directly simplifies the element integration to a monopole point source， and the computational efficiency is improved， but its over-simplification leads to the loss of accuracy. To address the above problems， a wave function superposition method based on the wave superposition method for planar near-field acoustic holography is proposed as an alternative to rectangular element integration. The method represents the integrated sound field of the rectangular element as the wave function form of the spherical wave spectrum of Helmholtz equation， and combines the nature of the spherical wave spectrum to interpolate the far-field spherical wave spectrum of the cell to the near field， thus obtaining the analytical expression of the explicit wave function of the external sound field equivalent to the integrated sound field of the rectangular element， effectively avoiding the numerical integration of the conventional wave superposition method and the oversimplification of the traditional equivalent source method. The reconstruction effects of the proposed method， the conventional wave superposition method and the conventional equivalent source method are compared using the near-field acoustic holographic algorithm of a rectangular simply supported plate. The results show that the reconstruction accuracy of the proposed method is higher than that of the conventional equivalent source method in all frequency bands， and the reconstruction accuracy in the high frequency bands is higher than that of the conventional wave superposition method， and its computational efficiency is significantly higher than that of the conventional wave superposition method.

Key words： near-field acoustic holography; wave superposition method; equivalent source method; wave function

（責任编辑：黎 娅）