AO辅助LSSVM的GNSS-IR土壤湿度反演方法

李信强,刘立龙,吴昊舰,张伊凡,郑明明

(1.桂林理工大学 测绘地理信息学院,广西 桂林 541006;2.广西空间信息与测绘重点实验室,广西 桂林 541006)

0 引言

土壤湿度是联系陆地和大气相互作用的关键因素[1],是水资源研究的重要参考标准,也是气象、水文以及农业环境中的重要参数[2]。研究土壤湿度对农业旱情监测、植被、地质灾害等相关研究都具有非常重要的意义[3]。传统的土壤湿度监测方法主要包括烘干称重法、时域反射仪(time domain reflectometer,TDR)、频域反射仪法(frequency domain reflectometer,FDR)等,这些方法不仅要求在实地操作,而且处理过程往往比较复杂,不适用于大范围内的土壤湿度测量,另外存在成本较高、效率低等缺点[4]。随着全球导航卫星系统(global navigation satellite system,GNSS)技术的发展,全球导航卫星系统多径干涉遥感技术(global navigation satellite system interferometric reflection,GNSS-IR)已经成为一种广泛应用于监测地表重要参数的新技术,在土壤湿度和雪深等领域中成为一种新型的遥感监测手段。

国内外学者已经对 GNSS-IR 技术有了很多的研究。2008年,Larson等[5]首次提出利用全球导航卫星系统多径干涉技术GNSS-IR 测量土壤湿度[6],该技术本质上是使用接收机所记录的信噪比(signal to noise ratio,SNR)数据对环境参数进行测量。Chew等[7]在实验中发现土壤湿度与信噪比的相位、振幅、频率均有一定的相关性,在裸土条件下,土壤湿度与相对延迟相位相比,振幅和频率的相关性更高。Liang 等[8]利用遗传算法的神经网络方法有效地整合多个卫星形成互补系统,经实验表明,该方法显著提高了土壤湿度反演的精度。在基于GNSS干扰信号幅值建立的土壤湿度反演模型中,2016年,文献[9-10]提出干扰效应和信噪比估算方法,并通过一系列实验进行了验证。之后,荆丽丽等[11]提出了一种将GPS卫星的两个频率数据加权融合进行反演的方法,其反演结果相较于单一频点的反演结果的精度有所提高。

然而上述研究存在土壤湿度值和反射信号的特征参量之间存在的模型较少且反演精度较低,无法得到高精度的土壤湿度值的问题。本文提出了将AO-LSSVM模型引入到GNSS-IR土壤湿度反演中,通过LSSVM算法可以对土壤表面粗糙程度以及植物微波散射产生一定的抑制作用,并引入天鹰优化器算法来优化LSSVM模型参数,提高了全局寻优和搜索能力,以此来寻找特征参量与土壤湿度的经验关系,从而提高土壤湿度反演的精度。本文将阐述AO-LSSVM模型土壤湿度反演的优势,然后通过实验与BP神经网络模型和PSO-LSSVM模型进行比较,并以PBO H2O项目组提供的土壤湿度数据作为精度评定的标准,来验证AO-LSSVM模型的有效性和可靠性。

1 模型原理与方法

1.1 GNSS-IR土壤湿度反演原理

GNSS-IR 土壤湿度测量是通过 GNSS 直射和反射信号的干涉效应来实现土壤湿度反演的一种遥感技术。在实地测量中,GNSS 接收机天线接收到的信号有来自卫星的直射信号,也有来自周围环境的反射信号。土壤湿度与反射信号的特征具有明显的相关性。当天线架设高度较低时,反射信号与直射信号具有相近的频率,由于受多路径效应影响,传播路径长度有所差异,因此来自卫星的直射信号和反射信号在进入GNSS接收机时产生了干涉效应[12]。

SNR 观测值是用来描述 GNSS 信号质量的重要参数,是衡量GNSS接收机接收信号强度的一个量值,受卫星信号发射功率、天线增益和多路径效应等因素的共同影响[13]。图1为GNSS接收机在同步接收直射信号与反射信号的原理示意图。

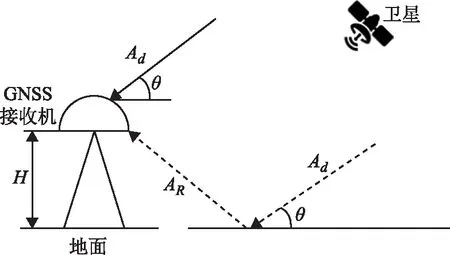
图1 GNSS-IR反射原理示意图

由图1可知,信噪比与信号幅值的关系如式(1)所示。

(1)

式中:AC表示合成信号振幅;Ad、AR分别表示直、反射信号的振幅;φ为直射信号与反射信号的相位差。去除SNR序列中的直射信号可以采用低阶多项式拟合的方法,从中分离出反射的分量,得出来的数据可以用于监测土壤湿度。图2是2016年第100天 PRN10卫星L2波段SNR信号的拟合图。

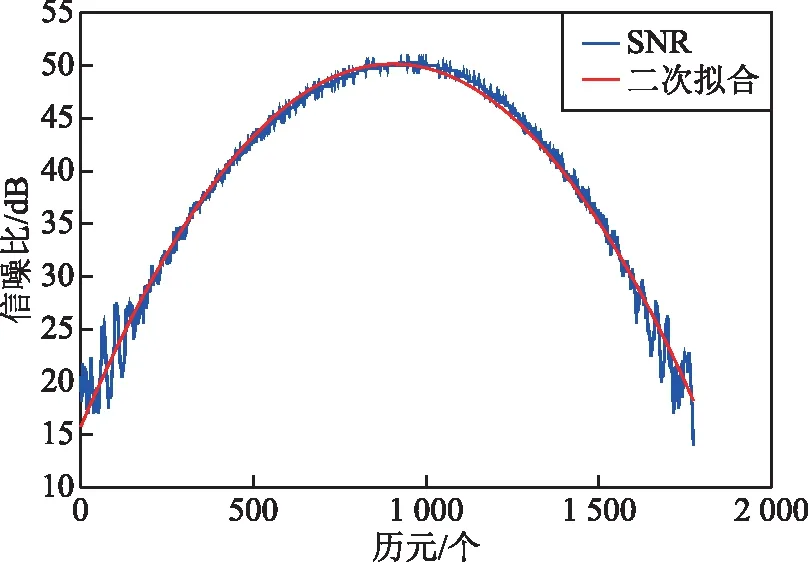
图2 PRN 10卫星的SNR信号拟合图

此时的反射分量SNRm可表示的关系如式(2)所示[14]。

(2)

式中:θ、λ分别为卫星高度角和载波波长;h为接收天线的等效高度;Am、φ分别表示反射信号的振幅和延迟相位。反射信号的幅值Am和相位φ可以采用最小二乘法拟合反射分量序列的SNR得到。Am和φ的大小受接收器周围的环境影响,由于反射系数受环境的变化而变化,反射系数对Am和φ的大小也会产生影响,所以,利用反射信号的幅值和相位可以实现土壤湿度的反演。图3为GNSS-IR土壤湿度反演基本流程图。

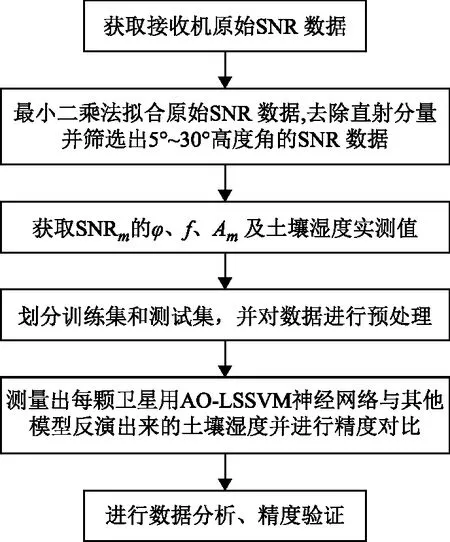
图3 土壤湿度反演基本流程图

1.2 AO-LSSVM原理

Suykens等[15]提出了在SVM的理论下进行改进的模型LSSVM,可以将不等式约束转化为等式约束,将二次规划问题转化为线性方程组问题,从而使该模型计算复杂度更低,预测精度更高。

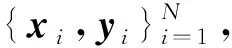
f(x)=ωTψ(x)+b

(3)

式中:ω为权函数;ψ(x)为非线性映射函数;b为偏置量。

2)根据结构风险最小化原则对LSSVM模型进行优化,如式(4)所示。

(4)

式中:J为风险目标函数;β′为惩罚因子;ξ为误差。

约束条件如式(5)所示。

yi=ωTψ(x)+b+ξi(i=1,…,N)

(5)

式中:β′为惩罚因子;ξ为误差。

3)由拉格朗日求目标函数,得出式(6)。

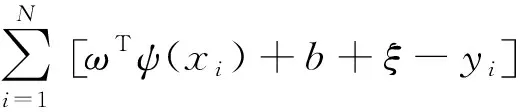
(6)

式中:α′为拉格朗日乘子。

4)根据优化条件,对拉格朗日参数分别求导,得出LSSVM模型函数,如式(7)所示。

(7)

式中:K(x,xi)为核函数。

本文采用的为径向基核函数RBF计算,如式(8)所示。

(8)

式中:σ2为核函数参数;e为常数。由于存在LSSVM最优参数难以确定的问题,本文采取天鹰优化器算法(aquila optimizer,AO)对其进行优化。

天鹰优化器算法是一种新型种群智能优化算法,采用4种狩猎方法,天鹰在不同情况下可以用不同的狩猎方法来回变化,具有全局寻优能力强,收敛速度快等优点[16]。

第一种方法是天鹰通过垂直弯曲的高空飞翔选择最佳狩猎区域,数学表达如式(9)所示。

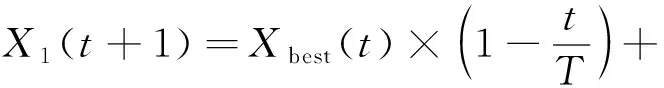
(9)

式中:X1(t+1)为天鹰使用第一种方法下一次迭代的解;Xbest(t)为迭代之前获得最优解;XM(t)为迭代时当前解的平均值;rand为[0,1]的随机值;t为当前迭代次数;T为最大迭代次数。

第二种方法是天鹰通过发现猎物并采取短滑翔攻击的等高线飞行的行为,数学表达如式(10)所示。

X2(t+1)=Xbest(t)×Levy+
XR(t)+(y-x)×rand

(10)

式中:X2(t+1)为天鹰使用第二种方法下一次迭代的解;XR(t)为N个位置内的随机解;Levy为飞行分布函数,其中

(11)

式中:s为一个常量0.01;u和v是0至1的任意数。σ′的计算如式(13)所示。

(12)

式中:β为常量值1.5;Γ(x)为伽马函数。

第三种方法是天鹰通过准备着陆并做好慢下降攻击的低飞行行为,数学表达如式(13)所示。

X3(t+1)=(Xbest(t)-XM(t))×α-
rand+((UB-LB)×rand+LB)×δ

(13)

式中:X3(t+1)为天鹰使用第三种方法下一次迭代的解;α和δ为较小值(0,1)的开采调整系数;UB、LB分别是待解决问题的上界和下界。

第四种方法是天鹰通过行走和抓取猎物进行俯冲的行为,数学表达如式(14)所示。

X4(t+1)=QF×Xbest(t)-(G1×X(t)×rand)-
G2×Levy+rand×G1

(14)

式中:X4(t+1)为天鹰使用第四种方法下一次迭代的解;X(t)为当前迭代的位置;QF为平衡策略的质量函数;G1为猎物逃跑时的各种行动;G2为从2至0的递减值。

天鹰优化器算法先使用第一种方法和第二种方法模拟天鹰在高空中飞行的行为来捕食,然后使用第三种方法和第四种方法模拟天鹰低空飞行状态的行为来狩猎。

天鹰优化器算法优化LSSVM参数的步骤流程图如图4所示。

2 实例分析

2.1 数据来源

美国板块边界观测网项目(plate boundary observatory,PBO)最初设计的目的是研究太平洋和北美板块的移动,同时监测地震和火山爆发等自然灾害。本文实验选取美国西部地区PBO的P043测站的监测数据进行土壤湿度反演。该测站位于美国怀俄明州的一处草原(43.881 1°N,-104.185 7°W),海拔1 490.933 m,年降水量为458 mm。接收机类型为TRIMBLE NETRS,天线类型为TRM29659.00,周围地形平坦且视野开阔,因此该测站适合监测土壤湿度。图5为P043测站的周围地表环境。图6为P043测站在PBO中心提供的气象站点数据以及降雨情况,该降雨数据为地表深处5 cm左右的土壤湿度值。

图5 P043测站周围地表环境图

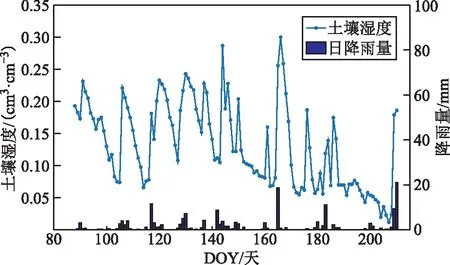
图6 土壤湿度参考值与降雨值

从图6可以看出,PBO提供的降雨量与土壤湿度变化趋势基本保持一致,显著降雨有6次,分别在第120天、130天、140天、160天、180天、210天,其中最大降雨量达到2.11 cm。在发生降雨后,在该时间段的土壤湿度值会明显上升,由此可知,土壤湿度值变化主要受降雨影响,在该时间段降雨量比较丰富,适合进行土壤湿度实验。

本实验在P043测站统计了4颗GPS卫星在2016DOY88—2016DOY210该时段的观测数据,L2C观测数据采集间隔为15 s。本文设定3种方案来验证AO-LSSVM的有效性和可靠性:方案1基于BP神经网络模型的土壤湿度反演;方案2基于PSO-LSSVM模型的土壤湿度反演;方案3基于AO-LSSVM模型的土壤湿度反演。本文将上述3个方案用决定系数(R2)、均方根误差(root mean square error,RMSE)、平均绝对偏差(mean absolute error,MAE)作为精度指标,以此验证AO-LSSVM模型的可行性。

2.2 数据处理

本文在P043测站利用TEQC对观测文件进行处理,分别获取了PRN10、PRN14、PRN18、PRN32 4颗卫星的SNR、高度角、方位角等数据,并用低阶多项式拟合原始SNR数据去除直射分量,并筛选出5°～30°高度角的SNR。将上述拟合筛选后的反射信号分量数据进行最小二乘拟合,获取反射信号分量的相位φ、频率f、振幅A。将其作为输入数据,实际的土壤湿度值作为输出数据,将2016DOY88—2016DOY210该时段的数据进行处理后得出122组数据,通过调试训练集和测试集的比例,最终确定训练集和测试集比例为3∶1时最优,通过随机抽取方法选出87组为训练集,35组为测试集,训练集和测试集互斥且没有交集。由于在实验中得出的反射信号分量3个特征向量中,相位与土壤湿度值的相关性最高,本文用相位作为3种方案的输入数据,实际的土壤湿度值作为3种方案输出数据,并通过精度指标来评价3种方案之间的精度差异。

2.3 结果分析

本文分别使用PRN10、PRN14、PRN18、PRN32 4颗卫星的数据构建成数据集并代入到AO-LSSVM模型中进行土壤湿度反演,图7为4颗卫星在AO-LSSVM模型下反演结果和土壤湿度真值的拟合图。

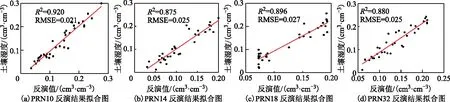
图7 3种模型反演结果拟合图

通过图7可以发现,PRN10、PRN14、PRN18、PRN32 4颗卫星的决定系数R2分别为0.920、0.875、0.896、0.880,反演结果与土壤湿度真值比较吻合,证明了AO-LSSVM模型在土壤湿度反演的领域中是可行和有效的。

为了进一步验证AO-LSSVM模型的优越性,在使用同一种数据的条件下,将BP神经网络模型、PSO-LSSVM模型和AO-LSSVM模型土壤湿度反演的结果和土壤湿度实测值进行对比分析,图8为4颗卫星在3种模型下反演结果和土壤湿度实测值的对比图。

通过图8中3种方案的拟合趋势可以发现,AO-LSSVM模型在总体上更加吻合土壤湿度真值的走势;BP神经网络虽然在整体趋势上较好,但是在个别天数与土壤湿度值还是有较大的偏差,可能由于样本数据量较小产生过拟合现象所致;PSO-LSSVM模型的反演效果相比BP神经网络模型较为理想,但整体依然不如AO-LSSVM模型,可能是由于PSO-LSSVM模型容易陷入局部最优解,从而导致精度较低。AO-LSSVM模型对土壤表面粗糙度及植被等环境因素产生一定的抑制作用,在相同数据集下,AO-LSSVM模型更适用于在小数据样本下GNSS-IR的土壤湿度反演,并且反演精度更高,泛化性能更强。

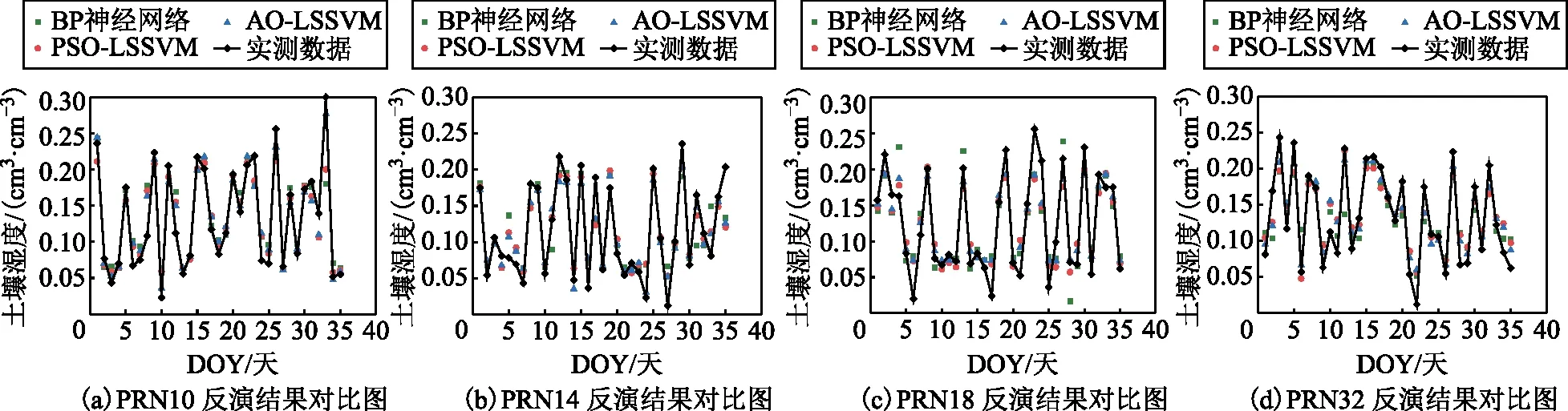
图8 3种模型反演结果对比图

表1为4颗卫星分别用3种模型进行反演结果的精度指标对比。通过表1可以明显看出,AO-LSSVM模型在决定系数、均方根误差以及平均绝对误差上相比BP神经网络模型和PSO-LSSVM模型精度都有一定的提高。限于篇幅,本文仅给出了PRN10卫星的分析。在PRN10卫星中,AO-LSSVM模型反演结果决定系数相比BP神经网络模型和PSO-LSSVM模型分别提高了13.58%和5.87%,均方根误差分别降低了52.38%和33.33%,平均绝对误差分别降低了29.41%和11.76%。结果进一步阐述了基于AO-LSSVM模型土壤湿度反演在决定系数和均方根误差上均有明显改善,证明该模型能够有效提高土壤湿度反演的精度。

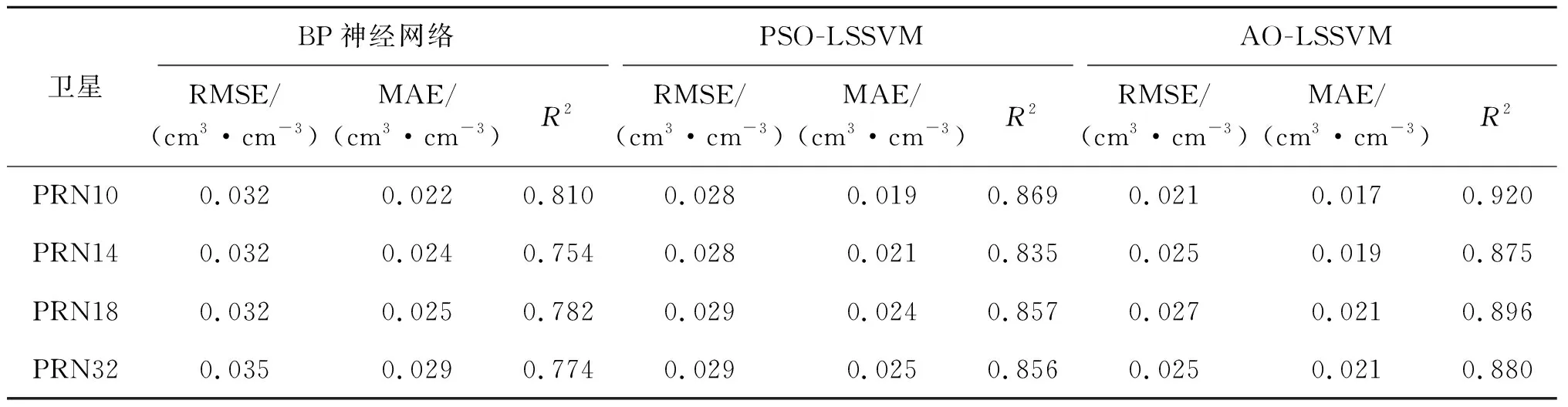
表1 4颗卫星3种模型反演精度对比

图9为PRN10卫星在3种模型下的反演结果与土壤湿度真值的绝对误差对比图,更加明确地证明了AO-LSSVM模型的精度要高于前两种模型。BP神经网络模型的平均绝对误差为0.022 cm3/cm3,PSO-LSSVM模型的平均绝对误差为0.019 cm3/cm3,AO-LSSVM模型的平均绝对误差为0.017 cm3/cm3,3种模型相比之下,AO-LSSVM模型的精度得到了有效提升。

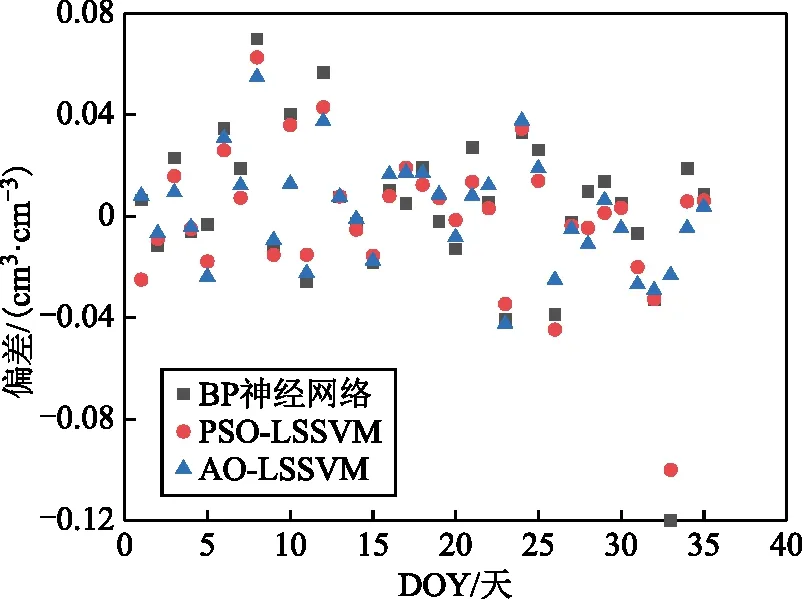
图9 3种模型绝对误差

3 结束语

本文针对土壤湿度反演精度较低的问题,提出一种基于AO-LSSVM模型进行土壤湿度反演的方法,并展开实验进行验证测试,结果如下。

GNSS反射信号的特征参量与土壤湿度之间存在着一定的相关性,在本实验中基于AO-LSSVM方法得到的PRN10卫星反演结果与土壤湿度真值之间的决定系数为0.920,均方根误差为0.021 cm3/cm3,平均绝对误差为0.017 cm3/cm3,与BP神经网络模型和PSO-LSSVM模型对比发现,决定系数分别提高了13.58%和5.87%,均方根误差分别降低了52.38%和33.33%,平均绝对误差分别降低了29.41%和11.76%。BP神经网络模型在样本数据量较少时可能会产生过拟合现象,PSO-LSSVM模型则容易陷入局部最优解,从而导致反演结果不够理想。因此,AO-LSSVM更适用于在小数据样本下GNSS-IR的土壤湿度反演,并且反演精度更高,泛化性能更强,进一步证明了该模型用于GNSS-IR土壤湿度反演的可靠性和优越性。本文后续将会加入其他算法来进行土壤湿度反演,旨在进一步提高GNSS-IR土壤湿度反演的精度。