输运理论中原子核初始化研究

周琦雅　郭文军

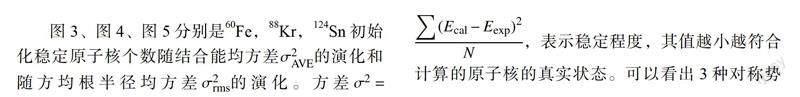
摘要：基于同位旋相关的量子分子动力学（IQMD）输运理论模型，研究中能重离子碰撞的初始化问题。成功的初始化可以很好地减少碰撞过程中出现的非物理涨落和虚粒子发射，有利于两体碰撞过程顺利进行。计算发现，不同的对称势对原子核的稳定性有一定的影响。选取不同质量数的Fe，Kr，Sn 元素及其同位素，通过其在自身平均场中随时间的演化来验证原子核的稳定性，统计出初始化稳定原子核的数量，选取出最为稳定的对称势。发现平方项的对称势 U2 最为稳定，其对应的斜率 L、不可压缩系数Ksym都在已知的约束范围内，表现出同位旋相关平均场取硬势时，原子核更为稳定的特征。

关键词：原子核初始化；IQMD 模型；对称势

中图分类号：O 571.6            文献标志码：A

Nuclear initialization in transport theory

ZHOU Qiya， GUO Wenjun

（College of Science， University of Shanghaifor Science and Technology， Shanghai 200093， China）

Abstract： Based  on  the  isospin  quantum  molecular  dynamics  （IQMD）  transport  theory  model，  theinitialization of intermediate energy heavy ion collisions was studied. The non-physical fluctuation andthe  emission  of  virtual  particles  in  the  collision  process  can  be  reduced  by  successful  initialization，which is conducive to the stability of the next two-body collision. Different symmetry potentials havecertain influence on the stability of nuclei. Fe， Kr， Sn and their isotopes with different mass numberswere selected， and the stability of nuclei was verified by the evolution with time in their own mean field.The  number  of  stable  nuclei  was  initialized  statistically，  and  the  most  stable  symmetry  potential  wasselected. The study shows that the symmetry potential U2 of the square term is the most stable， and itscorresponding slope L and incompressible coefficient Ksym are all within the known constraint range.When the isospin dependent mean field takes the hard potential， the nucleus is more stable.

Keywords： nuclear initialization; isospin quantum molecular dynamics （IQMD） model; symmetrypotential

對称能是指纯中子物质与对称物质的平均单核子能量之差，可以导致质子与中子的不同能量状态。它描述了原子核系统中，中质比变化时结合能的变化[1-2]。对称势与对称能通过能量密度泛函联系在一起，有一定的依赖关系。同位旋相关的量子分子动力学（ isospinquantummolecular dynamics ， IQMD）模型初始化中，选用不同的对称势，对称能也在变化，初始化出来的核子会产生差异。因而研究对称能和对称势对输运理论有重要作用。密度依赖的对称能对致密星有一定的影响，对斜率 L 和不可压缩系数Ksym敏感[3-4]。研究对称能的 L 和Ksym是十分必要的。 Li 等[5]用核状态方程研究了核对称能的Ksym?L （曲率?斜率），对此有利于理解中子星的性质，例如壳核跃迁、半径。Ksym?L 相关的天体物理性质有助于约束难以确定的核对称能量的高密度行为。中子星的半径由同位旋非对称物质的压力决定，压力受对称能斜率 L 的影响[6]。此外，对称能的斜率 L 还提供了密度依赖的对称能的很多重要信息[7]。

重离子在中高能的碰撞过程中可以提取出很多核性质，其过程一般通过弹核轰击靶核，对轰击后的产物、碎片进行分析得出结果。因而需要首先考虑初始核的稳定性，即原子核的初始化。有研究表明，在预测反应路径和相应可见物（如集体流）中观测到的差异，很大一部分是由于系统初始化和碰撞积分处理（主要是泡利阻塞效应）方面的差异造成的。在对同位旋敏感的重离子碰撞（ HICs ）的输运模型计算观测中，原子核的初始化也起着重要作用。例如，初始化时考虑中子皮会影响外围 HICs 中π?/π+比值的预测。对称势在原子核势能中是很重要的一项，修正对称势有利于初始化更多的原子核数量[8-10]。研究中能重离子碰撞过程，通常是建立输运模型。现如今，发展了很多输运模型，主流的有 Boltzmann-Uehling- Uhlenbeck（ BUU ）模型、量子分子动力学（QMD）模型及其扩展量子分子动力学（ EQMD）模型、同位旋相关的量子分子动力学（IQMD）模型、反对称分子动力学（ AMD ）模型、费米分子动力学（ FMD ）模型。 BUU 模型将核子看作点粒子， Gao 等基于 BUU 模型研究了在一定条件下带电介子比比自由中质比对称能的敏感度大，根据研究同位旋敏感可观测物的模型依赖关系，通过实验和理论模拟的比较确定核对称能的密度依赖性[11-12]。QMD 模型描述了反应系统的状态，提供了弹靶的碰撞和碎片的有关信息，根据哈密顿正则方程加上两体碰撞项计算系统的时间演化，能极好地描述碰撞系统从中等能量到相对论能量的时间演化过程。它包含平均场和两体碰撞。此外， QMD 模型追踪了每个核子的运动，在处理碎片的形成上很成熟。 QMD 模型将粒子看成高斯波包，用波包代表波函数，相较于经典的模型加入了量子概念，而中能核物理中量子效应十分普遍，并且该模型适用于很宽的能量范围，量级从 MeV 到 GeV 。EQMD 模型改进了 Pauli 势与波包宽度，在核子?核子碰撞过程中能够增强动态α的发射过程[13]。IQMD 模型是一个同位旋依赖的 QMD 模型，将质子、中子区分开，初始化中质子、中子分别具有独立的坐标。碰撞中，分别采用不同的核子?核子碰撞截面， Pauli 阻塞中考虑同位旋效应，势能中除了考虑库仑势还考虑了对称势。该模型适用于多体理论中能重离子碰撞的动力学行为，在描述中能重离子碰撞方面和核物质性质方面很成功[14-18]。郭文劈裂对原子核阻止有很明显的影响，镜像核发射率是较好的同位旋相关平均场的灵敏探针。 AMD 适合描述基态性质和反应过程[21-22]，FMD 是全波函数的反对称性框架[23-24]，它们都应用于模拟低能核反应。本文基于 IQMD 模型，探寻初始化与对称势及其 L，Ksym之间的内在关系。

1模型

描述重离子碰撞的 QMD 模型主要包含3个因素：密度相关的平均场、介质中核子?核子碰撞截面、Pauli 阻塞。基于 QMD 模型成功的多体理论，结合包含同位旋的平均场，并加入对称势和库仑势，本文采用了 IQMD 模型。 IQMD 模型程序包含3个部分：原子核的初始化、弹靶碰撞、 Pauli 阻塞效应。第一步为初始化，即对 N 个核子的6N 个空间和动量坐标赋值，根据以上信息可以得到基态原子核的其他物理性质。中高能重离子碰撞时间持续较长，所模拟的原子核系统可能“蒸发”掉，需要初始化得到的原子核稳定性好。大多数核反应在200 fm/c 时间内就已经结束，通常检验稳定性的方法是让其演化300 fm/c 左右，本文初始化采用的原子核稳定时间为500 fm/s。研究核结构需要考虑核密度，核密度与均方根半径、结合能有关。初始化500 fm/c 后，在每个步长内计算系统的均方根半径。将平均结合能以及均方根半径与结构模型和2020原子核结合能数据值比较，差异如果在正常范围内就认为这个核在演化中没有蒸发。本文基于2020年发布的核数据[25]（见表1），通过代入不同的对称势，挑选初始化稳定的原子核，得到能量最小态，减少虚粒子发射，避免原子核还未碰撞就已坍塌破裂，使其后续碰撞结果更加稳定。

核子的总有效势为[26]

式中： USky为Skyrme势；UYuk为表面项（ Yukawa 势）；UCoul为库仑势； UMDI为动量相关项；UPauli为 Pauli 势；USym为对称势。

F（u）用来描述对称势的大小和变化。其中， F1（u）= u ， F2（u）= u2， F3（u）= u1/2，3种对称势表达形式分别为

式中： c =32 MeV ，为对稱势强度系数；τz =1分别表示中子和质子； u =ρ/ρ0是原子核约化密度，其中ρ00.16 fm一3是原子核饱和密度；6是相对中子过剩。

式中：ρ，ρn，ρp 分别为核密度、中子密度、质子密度。对称势参数 L 代表密度依赖曲线在饱和密度处的斜率，它与平均动能、单核子势、密度、对称势有关，是对称势密度依赖中的重要信息。Ksym表示曲率，又叫压缩模量或者不可压缩系数，它与系统密度关系密切，是划分软势硬势的标准，数据大的称为硬势，反之为软势。值得区别的是：Ksym为对称势的曲率； K 为所有势能的曲率。 L ，Ksym的计算式如下：

对称势 U1， U2， U3在密度分布下斜率 L 和曲率Ksym是存在差异的，见表2。

图1为3种对称势的对称能（纵坐标为对称能 S，表示纯中子物质与对称物质的影响之差）随密度（横坐标）的变化关系，大量实验和计算所证明3根线交点的地方处为饱和密度，对称势为32 MeV。由图1可见，这些数值都在基于多体理论的预测范围之内。使用不同相互作用的非相对论和相对论多体方法的预测， L 和Ksym有不同的取值[27]。

2结果分析与讨论

较低能量的原子核碰撞，需要较多的时间，初始原子核需要在这样的时间内稳定，这样可以用来研究能量较低的原子核熔合反应。基于上述3种不同的对称势，从轻到重初始化了3种元素 Fe ，Kr ， Sn 的同位素，利用 IQMD 模型，令每个核子在自身平均场中随时间自由演化，通过比较各个时间的原子核结合能和方均根半径与实验的差值，来检验原子核的稳定性，统计出初始化稳定原子核的数量。

图2给出了52-60Fe ，76-88Kr ，108-132 Sn 的核素，在 IQMD 模型给出的结合能值与2020年数据给出的结合能值均方差在5%的范围内，分别用3种对称势计算了10000次。 N 为统计的原子核个数。可以看出， U2势得到的稳定的原子核数量最多，势函数的曲线更陡峭。 U2的 L 和Ksym值最大，体现了硬势的特点。L 与密度依赖相关，Ksym是划分硬势和软势的标准，此值越大，结合越强，表面耗散越小，所以得到了更多稳定的原子核。反之， U3的最少。图2均为上升趋势，不同元素、同一元素不同的同位素，原子核越重，结果越明显。 Sn 同位素能够初始化出来的核子最多，是因为轻核的密度较小，结合程度较小，容易碎裂；而重核的密度趋于恒定，相互作用力相对较大，不易断裂。

图3、图4、图5分别是60Fe ，88Kr ，124 Sn 初始∑（Ecal一Eexp）2化稳定原子核个数随结合能均方差 A（2）VE 的演化和 N随方均根半径均方差 rms（2）的演化。方差2=表示稳定程度，其值越小越符合计算的原子核的真实状态。可以看出 3 种对称势在60Fe ，88Kr ，124 Sn 之间的差别由 Fe 到 Sn 逐渐增大。由上述结合能及方均根半径的对比可知， IQMD 模型采用 U2势，能够对稳定核基态的大部分性质给出相当满意的描述。

3种对称势下，对 Sn 同位素链选取了最低的10个均方差取平均值，结果如图6所示。可以看出，无论是对于结合能还是方均根半径， U3的均方差平均值都是最大。均方差越大，表示变化量越大，偏差越大，越不稳定。 U2的最小，因而最稳定。图6清晰再现了上述图2、图3、图4、图5的结果。

从轻到重的不同元素结果都取得很好的一致性， IQMD 模型采用对称势 U2更稳定。 U2对称势对应的斜率 L、不可压缩系数Ksym最大是硬势，显示出更高的刚性，硬度大。此外，原子核的平均密度大约是2/3倍的饱和核密度， U2对称势在这个密度下的对称势最小，导致核子不易被排斥出。反之， U3是软势，软势核更容易形变，不稳定，易碎裂。

3结论

使用3种软硬程度不同的对称势，选取 Fe，Kr ， Sn 元素计算稳定的原子核数量。研究结果表明， U2势在轻重核元素初始化时核最稳定，并且对应的斜率 L、不可压缩系数Ksym都在已知的约束范围内，表现出同位旋相关平均场的硬势，原子核更为稳定，说明选用的平方对称势的合理性。成功的初始化可以很好地减少碰撞过程中出现的非物理的涨落和虚粒子的发射，使后续两体碰撞更稳定。

參考文献：

[1] LI B A， CHEN L W， KO C M. Recent progress and new challenges in isospin physics with heavy-ion reactions[J]. Physics Reports， 2008， 464（4/6）：113–281.

[2] LI B A， KO C M， BAUER W. Isospin physics in heavy-ion collisions at intermediate energies[J]. International Journal of Modern Physics E， 1998， 7（2）：147–229.

[3] CAVAGNOLIR，MENEZESDP，PROVID?NCIAC. Neutronstarpropertiesandthesymmetryenergy[J]. Physical Review C， 2011， 84（6）：065810.

[4] PIEKAREWICZJ. Correlatingthegiant-monopole resonancetothenuclear-matterincompressibility[J]. Physical Review C， 2002， 66（3）：034305.

[5] LIBA，MAGNOM. Curvature-slopecorrelationof nuclear symmetry energy and its imprints on the crust-core transition，radius，andtidaldeformabilityofcanonical neutron stars[J]. Physical Review C， 2020， 102（4）：045807.

[6] LI B A， STEINER A W. Constraining the radii of neutron starswithterrestrialnuclearlaboratorydata[J]. Physics Letters B， 2006， 642（5/6）：436–440.

[7] XU C， LI B A， CHEN L W. Symmetry energy， its density slope， and neutron-proton effective mass splitting at normal density extracted from global nucleon optical potentials[J]. Physical Review C， 2010， 82（5）：054607.

[8] COLONNAM，ZHANGYX，WANGYJ，etal. Comparison of heavy-ion transport simulations： mean-field dynamics in a box[J]. Physical ReviewC， 2021， 104（2）：024603.

[9] YANG J P， ZHANG Y X， WANG N， et al. Influence of the treatment of initialization and mean-field potential on the neutron to proton yield ratios[J]. Physical Review C， 2021， 104（2）：024605.

[10] XU J， CHEN L W， TSANG M B，et al. Understanding transport simulations of heavy-ion collisions at 100A and 400A MeV： comparison of heavy-ion transport codes under controlled conditions[J]. Physical ReviewC， 2016， 93（4）：044609.

[11] GAO Y， YONG G C， WANG Y J， et al. Influence of the symmetryenergyonthecone-azimuthalemission[J]. Physical Review C， 2013， 88（5）：057601.

[12] GUOWM，YONGGC，WANGYJ，etal. Model dependenceofisospinsensitiveobservablesathigh densities[J]. Physics Letters B， 2013， 726（1/3）：211–217.

[13] MARUYAMA T， NIITA K， IWAMOTO A. Extension of quantum molecular dynamics and its application to heavy- ioncollisions[J]. PhysicalReviewC， 1996， 53（1）：297–304.

[14] CHEN L W， ZHANG F S， JIN G M. Analysis of isospin dependenceofnuclearcollectiveflowinanisospin- dependent quantum molecular dynamics model[J]. PhysicalReview C， 1998， 58（4）：2283–2291.

[15] HARTNACK C， PURI R K， AICHELIN J， et al. Modelling the many-body dynamics of heavy ion collisions： present statusandfutureperspective[J]. TheEuropeanPhysical Journal A - Hadrons and Nuclei， 1998， 1（2）：151–169.

[16] YAN T Z， LI S. Impact parameter dependence of the yield ratiosoflightparticlesasaprobeof neutronskin[J]. Nuclear Science and Techniques， 2019， 30（3）：43.

[17] WANGSS，MAYG，CAOXG，etal. Hard-photon productionanditscorrelationwithintermediate-mass fragmentsinaframeworkofaquantummolecular dynamicsmodel[J]. PhysicalReviewC， 2020， 102（2）：024620.

[18] YANTZ，LIS，WANGYN，etal. Yieldratiosand directedflows of light- nucparticlesfromprotonrichlei-inducedcollisions[J]. NuclearScienceandTechniques， 2019， 30（1）：15.

[19]林琳， 郭文军， 黄璐.中能重离子反应中中子–质子有效质量劈裂的研究[J].上海理工大学学报 ， 2017， 39（6）：532–538.

[20]孙克 ， 郭文军.中能重离子碰撞过程中的镜像核发射率[J].上海理工大学学报， 2020， 42（3）：224–231.

[21] PIANTELLIS，OLMIA，MAURENZIGPR，etal. Comparison between calculations with the AMD code andexperimental data for peripheral collisions ofNb + Nb，Snat 38 Mev/nucleon[J]. PhysicalReviewC， 2019， 99（6）：064616.

[22] ONO A， HORIUCHI H， MARUYAMA T， et al. Fragment formationstudiedwithantisymmetrizedversionof moleculardynamicswithtwo-nucleoncollisions[J]. Physical Review Letters， 1992， 68（19）：2898–2900.

[23] FELDMEIERH，BIELERK，SCHNACKJ. Fermionicmoleculardynamicsforgroundstatesandcollisionsof nuclei[J]. Nuclear Physics A， 1995， 586（3）：493–532.

[24] BACCA S， FELDMEIER H， NEFF T. Long range tensor correlationsinchargeandparityprojectedfermionic molecular dynamics[J]. Physical ReviewC， 2008， 78（4）：044306.

[25] WANG M， HUANG W J， KONDEV F G， et al. The AME 2020 atomicmassevaluation （II）. Tables，graphsand references[J]. Chinese Physics C， 2021， 45（3）：030003.

[26] LIUHL，MAYG，FANGDQ. Finite-sizescaling phenomenonofnuclearliquid-gasphasetransition probes[J]. Physical Review C， 2019， 99（5）：054614.

[27] OERTEL M， HEMPEL M， KL?HN T， et al. Equations of stateforsupernovaeandcompactstars[J]. Reviewsof Modern Physics， 2017， 89（1）：015007.

（編辑：董伟）