基于层次结构模型的系统寿命评估方法研究
沈恒龙,罗平,杨子亮,戴晶晶,李萌萌
(广电计量检测集团股份有限公司,无锡 214111)
引言
复杂装备是高度综合、复杂和集成的大型系统,它由若干个分系统和设备组成,每个分系统和设备又包含数以万计的零部件[1]。复杂装备的系统寿命与其寿命剖面、任务剖面、使用环境及维修保障方案等因素密切相关,且鲜见广泛通用的数学统计模型,导致统计试验难以组织实施。若通过收集现场使用数据的方法评估设备的寿命年限,则由于寿命年限指标较长,导致观测周期跨度大,且评估对象数量多,试验保障资源耗费量大。现阶段复杂装备的寿命评估主要有两种方法,一种是采信装备承制单位的寿命分析评估报告,另一种是采用相似产品法进行定性的类比分析,这两种方法简单易执行,但是评估的真实性和科学严谨性容易受到广泛的质疑。本文基于层次结构模型,结合相似产品法,给出了一种改良的系统寿命评估方案。
1 层次结构模型的基本结构
层次结构模型可以将需要决策的复杂系统问题相互关联的要素按隶属关系分解成目标、准则、方案等层次,在此基础上进行定性和定量分析的一种决策方法。在对方案评价时,它对各备选方案中所有因素两两比较,确定其相对重要性值,再通过求所有因素的相对重要性值与该因素权值之积并累加的方式即可得出对所有备选方案的相对优劣程度赋[2]。
2 基于层次结构模型的系统寿命评估方法
2.1 基于层次结构模型的系统寿命评估模型
采用层次权重决策分析方法量化各因素对系统寿命的重要程度,综合考虑多种特征属性[3],包括:功能、结构、材料、工艺、贮存环境。建立的层次结构模型如图1 所示。

图1 评估对象与类比对象梯阶层次结构示意图
依据模型,首先确定类比对象。类比对象一般选取评估对象的相似产品,参与本次评估的类比对象数量应不少于2,类比对象所能提供的数据应真实有效,可查询。类比对象的特征属性信息包括但不限于结构、功能、材料、工艺、贮存环境、维修保障方案等,并与评估对象具有可比性。
直接将两型复杂装备进行类比分析,数据量较大,故通过环境严酷程度和工作时间长短对比,确定一组可能的最短寿件,结合寿命评估的最短寿零部件假设进行寿命评估。利用已服役一定年限的相似产品的同类型最短寿件作为类比对象,通过类比对象的系统寿命评估现有装备的系统寿命。
确定完评估对象和类比对象后,对影响寿命的各特征属性进行权重分配,构造准则层对目标层的比较判断矩阵。然后对评估对象和类比对象的各特征属性进行对比,将不同因素两两比较,构造相应特征属性比较判断矩阵。判断矩阵的构造方法及方案层对准则层的比较判断矩阵同理[4]。
对于涉及相对复杂问题的决策,不同因素的比例通常是不同的。1~ 9 及其倒数通常被用作比较两个不同影响因素的标准,从而定义比较判断矩阵A=(aij)n×n。且比较判断矩阵有如下性质:
以准则层对目标层的比较判断矩阵为例。
首先,采用雅克比(Jacobi)法计算判断矩阵的最大特征值然后,定义一致性指标CI 为:
在应用层次分析法构造出判断矩阵时,需先对判断矩阵进行一致性检验,当一致性比率CR <0.1 时,则通过一致性检验,否则需要重新调整判断矩阵直至满足一致性。定义一致性比率为:
式中:
RI—平均随机一致性指标,查表1 获得[5]。

表1 随机一致性指标
对特征向量进行归一化处理,归一化处理后的特征向量wA应使其分量满足:
将方案层对准则层的排序权重计算结果汇总,矩阵W(m,n)是以方案层对准则层的权向量为列向量组成的矩阵。因此方案层对目标层的总排序权向量为:
然后对总排序权向量w总进行一致性检验,总排序权向量的一致性检验规则如下:
当符合一致性要求后,即可用来判断各方案层对目标层的优先次序。根据总排序权向量的分量取值,用表示评估对象权重,分别表示类比对象1、类比对象2 的权重。
2.2 评估结果判定要求
当满足以下要求时,即可判断相应评估对象寿命年限是否满足要求。
式中:
T—相似对象已达到的寿命年限,单位为年。
3 案例分析
本文以某通信设备为工程案例进行寿命分析,经过分析论证,新研制型号(评估对象)较相似2 型产品(类比对象)的信道接收单元在功能、结构、材料、工艺和环境等方面均有不同程度的改进或更改,且新研制型号规定寿命年限≥5 年。根据服役中2 型产品(类比对象)的寿命统计,T类比对象1≥5.24 年,T类比对象2≥4.65 年。
根据本文第2.1 节的寿命评估模型,首先建立准则层(B 层)之间的判断矩阵,并对其进行一致性检验,结果见表2。各指标层面矩阵及一致性检验结果见表3~表7。

表2 判断矩阵及一致性检验

表3 B1 功能层面指标矩阵及一致性检验

表4 B2 结构层面指标矩阵及一致性检验

表5 B3 结构层面指标矩阵及一致性检验

表6 B4 结构层面指标矩阵及一致性检验

表7 B5 环境层面指标矩阵及一致性检验
方案层相对指标层的权重矩阵见表8。
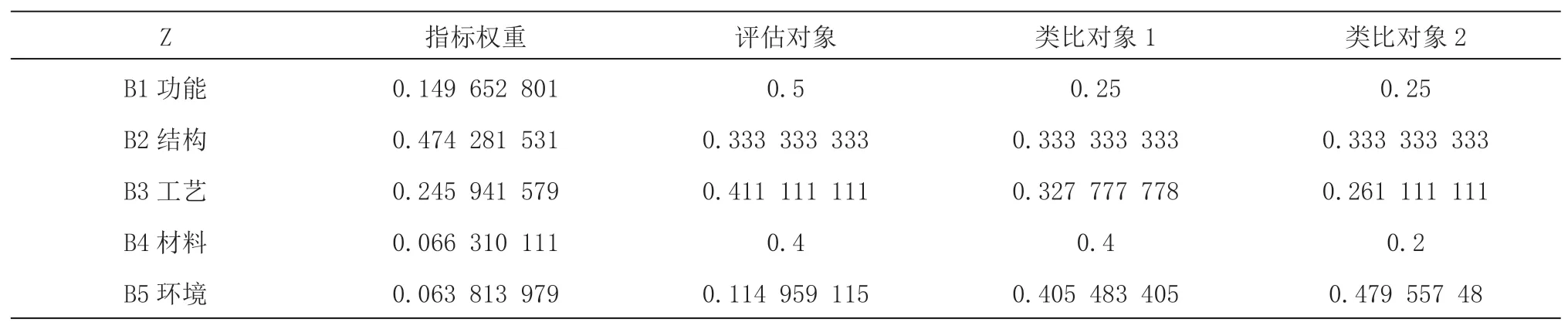
表8 权重矩阵
计算得总排序权向量为:
根据本文2.2 节的评估结果判定方法,本次评估对象的寿命评估结果如下:
根据以上论证,本次评估对象的寿命满足≥5 年的指标要求。
4 结论
基于层次结构模型的系统寿命评估方法给复杂系统的寿命评估提供了一种选择,但该方法局限性较大,故寻求一种更通用的系统寿命评估方法就显得十分必要,例如通过系统寿命的概率密度函数对系统寿命进行估计,或者在已知部件寿命的情况下,高效快速地得到其系统寿命相关封闭表达式就值得进一步的研究。

