冲击响应谱试验夹具动力特性研究

李旭，庞家志，王硕

（航天科工防御技术研究试验中心，北京 100854）

引言

航天器在寿命周期中需经受爆炸分离等冲击环境，据NASA 有关数据统计，爆炸冲击是导致航天器故障的主要原因之一。该环境下产生的应力波往往会给航天器的结构和功能带来不利的影响。因此为考核航天器的冲击环境适应性，需要进行充足的地面试验。

冲击响应谱试验（简称：冲击谱试验），是一种响应等效的试验方法。不同于经典冲击，该方法更注重冲击对系统的损伤势，不对冲击的输入波形和产生方式做固定要求，目前已逐渐成为主流的地面冲击试验方法。

自1932 年Biot 第一次引入冲击谱的概念后，大量的工程技术人员投入到冲击谱相关研究中。主要集中在冲击谱算法、冲击谱试验机研制、试验标准编制等方面[1-5]，关于冲击谱夹具的研究内容则比较少。2011 年石蒙等[6]采用有限元对夹具进行动态特性设计，结果表明振动台配合所设计的夹具可得到一定量级的谐振响应。2016 年沈志强等[7]通过设计优化冲击台面结构，将冲击谱量级由1 000 g 提升到2 000 g，并进行了负载试验，提升了振动台的冲击谱试验能力。2017 年郭健龙等[8]说明了夹具连接方式对振动台冲击谱模拟能力的影响。2018 年薛杰等[9]对L 形夹具进行有限元分析，结果表明修正后的模型可对冲击谱试验的响应正确预示。虽然关于冲击谱夹具的研究内容较少，但是为使冲击谱试验更为合理，传感器监测点的安装位置已经逐渐从试验机台面转到产品夹具上。夹具的设计及其动力特性与试验的开展息息相关。因此亟待开展该方面内容的研究。

本研究以冲击谱试验原理为依据，设计并搭建气动冲击谱试验系统。以钢制夹具板作为冲击对象，进行了不同工况下的对比试验，分析了冲击谱试验夹具的动力特性。研究结果对试验夹具的设计和试验的实施具有一定借鉴意义。

1 冲击谱试验系统分析原理

1.1 冲击谱原理及算法

如图1 所示，冲击谱可描述为，将冲击激励施加在一系列固有频率不同的单自由度质量-弹簧-阻尼系统上。计算这些单自由度的最大响应值，并以固有频率为横坐标，最大响应值为纵坐标绘制曲线，得到的谱形即为冲击谱。

1.2 改进的递归数字滤波法

冲击响应谱有直接积分，傅里叶变换，递归数字滤波和改进的递归数字滤波等多种计算方法。其中改进的递归数字滤波法引入广义斜台函数，建立了绝对加速度模型和相对位移模型，将模型转化成递归公式，并通过递归公式计算冲击谱值。

广义斜台函数为：

式中：

u（t-mT）—单位阶跃函数；

A—斜率；

t—时间；

T—采样间隔。

模型可表示为递归公式：

式中：

ωd—有阻尼固有频率；

ωn—固有频率；

ξ—阻尼比；

对于绝对加速度模型：

对于相对位移模型：

当固有频率远小于采样率时，b0，b1，b2→0，a1→-2，a2→1。

递归公式可表示为：

式中：

在这种形式下：

目前改进的递归数字滤波法凭借其计算速度快、精度高的优点，已经成为冲击谱的主流计算方法，后文中的冲击谱均使用该方法进行计算。

2 冲击谱试验系统与有限元模型建立

2.1 冲击谱试验系统建立

气动冲击谱试验系统组成如图2 所示，开启高压气瓶阀门，使高压气体进入动力装置，通过压力控制系统调节气压压力值，达到理想数值后瞬间释放气体，推动质量块快速运动，撞击冲击台面，能量通过冲击台面传递至工装夹具板，加速度传感器采集加速度信号后，处理模块将加速度时域信号进一步计算，得到冲击谱。

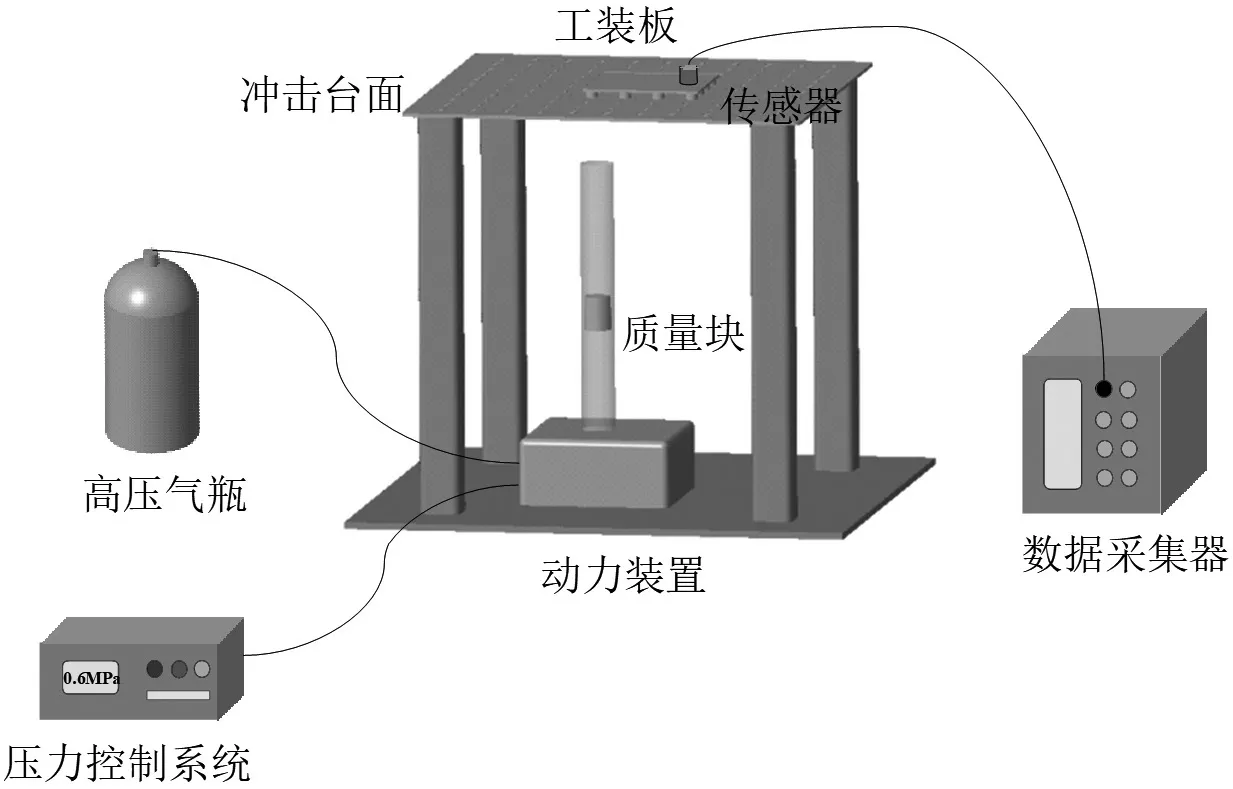
图2 气动冲击谱试验系统

2.2 有限元模型建立

为获得被冲击结构的固有频率及振型等参数，需要建立相应的有限元模型进行模态仿真计算。

冲击台面和夹具的有限元模型如图3 所示，材料属性为钢，密度为7 850 Kg/m3，弹性模量为2e11Pa，泊松比为0.3。边界条件为冲击台面四角孔位刚性固定。

图3 有限元模型和边界条件

3 试验及结果分析

试验工况的变量为：冲击能量（气体压力）、采集位置和冲击位置。其中采集位置和冲击位置如图4 所示，圆形表示采集位置，三角形表示冲击位置。采样时间为0.16 s，采样频率为102 400 Hz，阻尼比ξ=0.05，计算冲击谱的下限频率为100 Hz，上限频率为5 000 Hz。

图4 冲击和采集位置

3.1 冲击能量对冲击谱的影响

设计工况为冲击位置为2 号冲击点，采集位置为2 号采集点。通过气压调整冲击能量，冲击气压分别为0.4 MPa，0.5 MPa，0.6 MPa。采得的加速度信号，计算得到的冲击谱如图5 所示。

图5 不同冲击量级冲击谱

从图5 中可知气体压力越大，得到的冲击谱整体量级越高。分析可知，冲击气压越大，质量块获得的能量越大，在撞击冲击台面后，能量从冲击台面传递至夹具的加速度越大，进一步计算得到的冲击谱量级越高。

3.2 不同采集位置的冲击谱

设计工况冲击位置为1 号冲击点，冲击气压为0.4 MPa，采集位置为1~5 个采集点。采得的加速度信号，分别计算各位置的傅里叶变换频谱和各位置的冲击谱，如图6 所示。

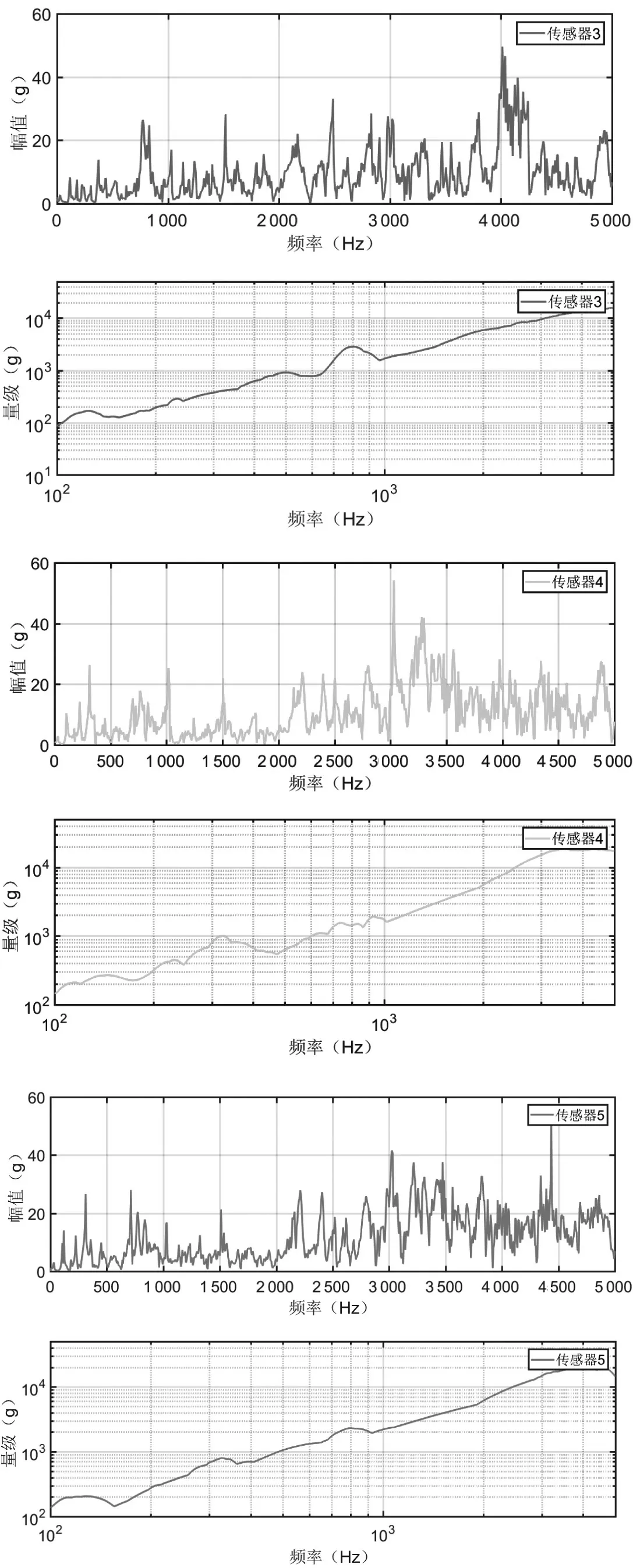
图6 不同采集位置的傅里叶变换频谱和冲击谱（续）

图6 不同采集位置的傅里叶变换频谱和冲击谱

分析图6 可知，不同位置的冲击谱不同，当冲击信号的频谱含多个峰值且各峰值的幅值相差不大时，系统各阶模态被激起的情况较为复杂，计算得到的冲击谱在对数坐标系下拐点不明显。当存在某一频带幅值较大，其他频带幅值较小时，冲击谱会在该频带出现拐点，如传感器1 的响应频谱在710 Hz 左右出现明显的尖锋，对应冲击谱在710 Hz 左右的凸起。如图7 所示，传感器的安装位置出现明显的局部模态。结构在该阶的固有频率为700 Hz，与试验结果相近。

3.3 冲击位置对冲击谱的影响

设计工况为冲击位置分别1 号冲击点和2 号冲击点，冲击气压为0.4 MPa，采集位置为1 号采集点。采得的加速度时间历程曲线和计算得到的冲击谱如图8 所示。

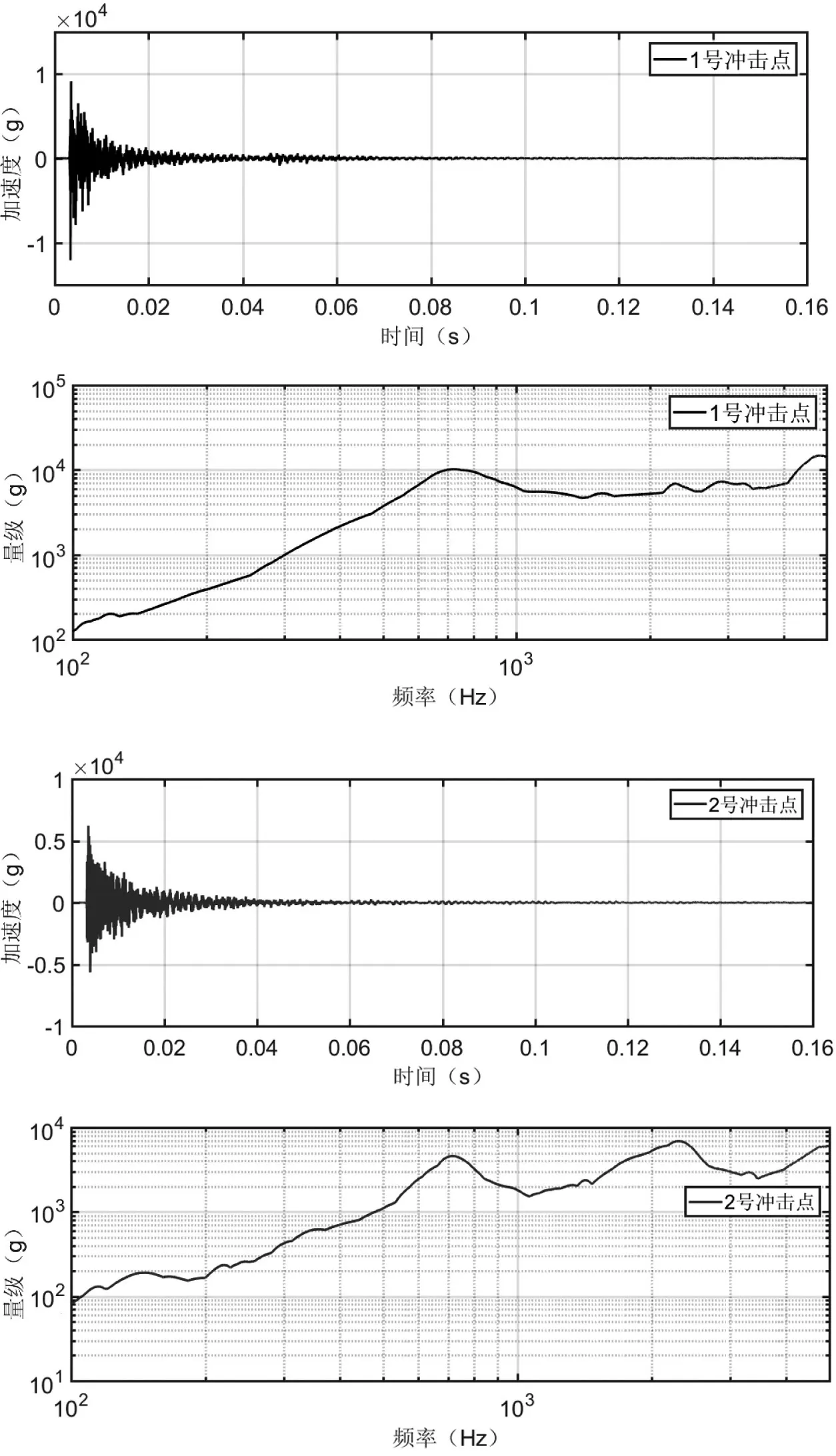
图8 不同冲击位置时间历程曲线及冲击谱

从图8 可知，冲击在台面的不同位置时，夹具板中间位置的冲击谱拐点频率并未发生明显变化，即该阶模态同样被激起。但冲击谱的量级发生改变，冲击在1 号点时比在2 号点的量级整体偏大。

4 结论

本研究以冲击响应谱原理为依据，设计并搭建了冲击谱试验系统，设计钢制夹具板为被冲击对象，进行了不同工况下的试验，结果表明：

1）冲击气压的高低与冲击谱量级的高低相关，当冲击气压增加时，推动质量块的能量增加，撞击后计算得到的冲击谱量级也会相应增加。

2）夹具的模态响应与冲击谱拐点密切相关，当结构的某阶模态被激起，且该频率的幅值远高于其他频率幅值时，冲击谱会在该频率附近的频带内形成凸起状的拐点。

3）同一冲击工况下夹具的不同位置的冲击谱不尽相同，同时改变冲击激励点的位置也可导致冲击谱的变化。

综上所述，在对航天器开展冲击考核时，应合理设计夹具，使夹具冲击谱拐点与目标谱相近。另外应调整合适的气压大小和冲击位置，使冲击谱量值及谱形达到目标谱容差范围内。经过充分的预试验调试，满足试验技术条件要求后，方可对被试品开展正式冲击谱试验。