融合相似用户、物品的矩阵分解推荐算法研究

洪昶 刘伟 吕昊宸

摘要：推荐系统中传统的协同过滤算法和基于矩阵分解的推荐算法都单独地进行相关推荐，但两种方法独立运行，都存在一定的不足，导致推荐质量不佳。为了进一步提升推荐算法性能来提高推荐准确度，文章提出一种融合相似用户、物品的矩阵分解推荐算法，在矩阵分解模型的基础上，结合协同过滤思想来挖掘目标用户的个性化候选物品推荐。文章采用MoviesLens数据集进行模型训练并评估其性能，与原有的方法相比，推荐准确度获得了进一步提升。

关键词：推荐系统；协调过滤；矩阵分解

中图分类号：TP3  文献标志码：A

0 引言

随着信息时代的飞速发展，人们不得不开始面对信息过载的问题［1］。如何快速并准确地获得个人感兴趣的信息成为现代研究的一个重点问题。人们亟须从传统的“人找信息”的方式转变为“信息找人”的方式，推荐系统的提出为现代信息索引方式提供了一种有效的解决方案。推荐系统中比较常见而有效的推荐算法分为协同过滤和矩阵分解两类方法［2-3］。传统的协同过滤分为基于用户和基于物品的协同过滤方法，此类方法的本质就是通过用户和物品的评分信息，构建交互信息向量两两向量之间计算相似度，通过相似度进行相关推荐。这种算法计算流程简单，易于实现，但由于交互向量的稀疏性，计算相似度时会降低推荐结果质量。基于矩阵分解的推荐算法将评分矩阵分解为较小的用户兴趣矩阵和物品属性矩阵的乘积。这样，即使某两个用户或者物品之间没有相同交互项，但能通过其他用户或者物品的共现信息进行表示向量学习，进而产生推荐。但缺点是忽略了相似用户或者物品间的协同过滤信息，限制了推荐质量上限。因此结合上述两种算法的优缺点，本文设计了一种融合方法，使两种算法进行相互补充来获得更高质量的推荐结果。

1 模型

1.1 用户、物品相似度计算

传统的协同过滤推荐算法首先需要通过相似度计算，找到用户或物品的相似项，然后为目标用户进行推荐。如何计算相似度成为整个协同过滤算法的核心。以基于用户的协同过滤方法为例，一种可靠的方法是通过两两用户间的行为向量的余弦相似度进行相似度计算，其公式如下：

simuv=|N（u）∩N（v）||N（u）||N（v）|（1）

其中，N（u）表示用户u有过行为的物品集合，N（v）表示用户v有过行为的物品集合。公式（1）只考虑了用户间交互项目的交集，而没有考虑用户对交互项评分的信息。例如，用户u和用户v对同一项目打分为5分和3分，虽然交互项相同，但用户偏好并不一样，因此对应的相似度也应不一样，Pearson相似度被引入来处理这类情况，计算公式如下：

simuv=∑i∈Iuv（rui-r-u）（rvi-r-v）∑i∈Iuv（rui-r-u）2∑i∈Iuv（rvi-r-v）2（2）

其中，Iuv表示用户u和用户v都交互过的项目，rui代表用户u对物品i的评分。本文后续涉及的用户间、项目间相似度计算均采用公式（2）所描述的方法。

1.2 基于用户的协同过滤

基于用户的协同过滤算法需要首先构建用户—项目评分矩阵，然后将评分矩阵中的每一行评分作为一个用户的向量表示，采用公式（2）描述的相似度计算，计算目标用户和其他用户之间的相似度，通过相似度的降序排序得到目标用户的K个最相似用户，从这K个用户交互历史中，选取N个候选物品推荐给目标用户，完成个性化推荐。其中，这N个候选物品需要过滤掉目标用户已经交互过的项目。

1.3 基于物品的协同过滤

基于物品的协同过滤算法，与1.2所描述的方法类似，不同之处在于其将评分矩阵中的每一列评分作为一个物品的向量表示，采用公式（2）描述的相似度计算，计算物品间的相似度，通过相似度的降序排序得到每个物品最相似的物品列表排序，当目标用户对某一物品产生交互后，就可以找到与该物品最相似的N个物品推荐给目标用户。同样，这些推荐物品也应该过滤掉目标用户已交互过的物品。与基于用户的协同过滤相比，这种方法方便冷启动，只要新用户对某一物品感興趣，就可以立即推荐相似物品，并且可以通过相似物品为用户做出可解释推荐。

1.4 矩阵分解

传统的协同过滤方法依赖表示向量之间的交集计算相似度，但由于表示向量交集较小，导致模型泛化能力有限，没有交集的用户或者物品之间的相似度一定为0，限制了模型性能。BiasSVD从拟合评分矩阵已有交互数据出发［4］，通过学习用户和物品向量矩阵来预测评分矩阵未交互部分，形式化描述如下：

r^ui=μ+bu+bi+qTupi（3）

该算法假设评分偏置来自用户物品无关的评分偏置μ、用户偏置项bu和物品偏置项bi 3部分。qu代表用户隐向量表示，pi代表物品隐向量表示，r^ui表示用户u对物品i的预测评分。通过优化模型损失函数可以学习到用户、物品隐向量，优化损失如下：

minp，q，b，u∑（u，i）∈Trui-r^ui2+λ（‖qu‖2+‖pi‖2+bu2+bi2）（4）

其中，rui表示真实评分，λ为正则系数，一般取λ为1。

1.5 融合相似用户、物品的矩阵分解

传统的协同过滤算法由于评分矩阵的稀疏性无法达到很好的泛化效果，限制了模型性能上限。矩阵分解算法又忽略了相似物品和相似用户间的协同过滤信息，因此，本文提出一种融合这两种算法优势的融合矩阵分解方法，首先通过1.1节描述的Pearson相似度计算每个用户物品的相似项，然后利用相似用户和相似物品增强矩阵分解中的协同过滤信息，改进矩阵分解中的预测公式如下：

r^ui=μ+bu+bi+

（qu+∑m∈Nuqm）K+1T（pi+∑n∈Nipn）K+1（5）

其中，Nu表示目标用户u最相似的K个用户，Ni表示候选物品i最相似的K个物品。优化公式（4）的模型损失函数得到用户和物品的隐向量表示完成模型训练。矩阵分解推荐算法流程如图1所示。

2 實验

2.1 数据集与评估指标

本文使用MovieLens电影推荐数据集来验证所提算法的优越性。数据集总共包含10万条用户对电影的评分信息，评分值为1～5，详细统计指标如表1所示。模型评估指标采用TOP N推荐［4］中最常用的准确率（Precision）和召回率（Recall）［5］。

2.2 实验结果与分析

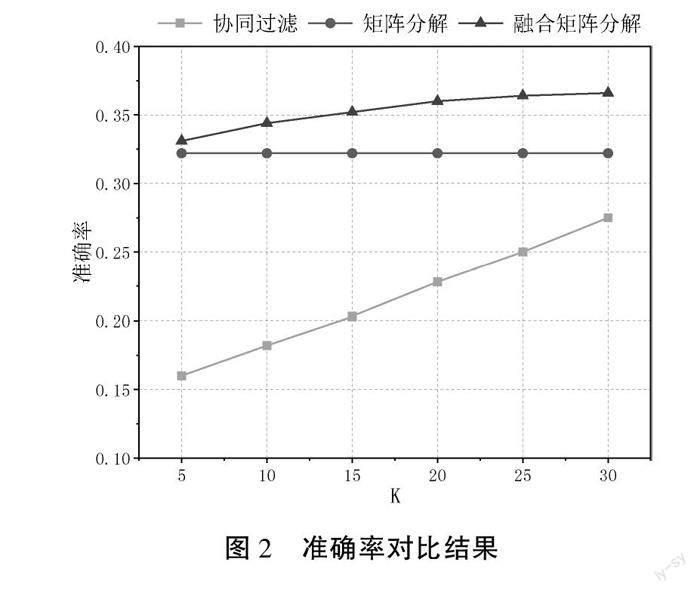
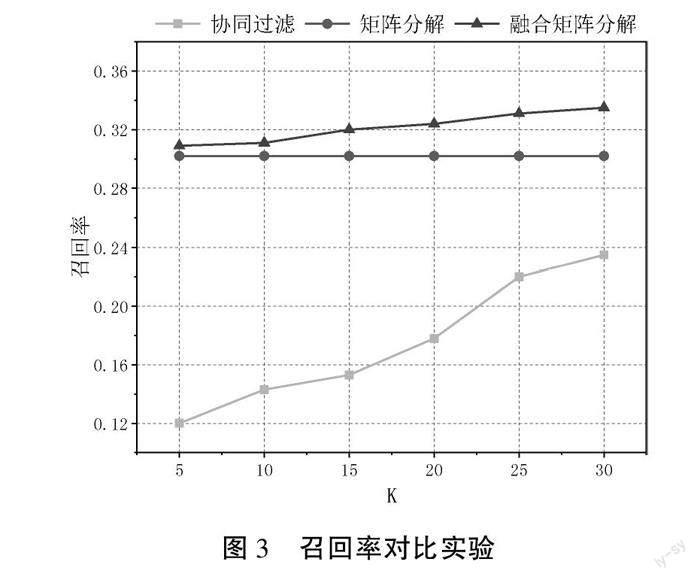
在融合矩阵分解推荐算法中，推荐物品数设置为20，相似用户和物品数K依次设置为5，10，15，20，25，30，对比评测结果如图2—3所示，横坐标K表示推荐物品数目的设置。

本文从融合相似用户、相似物品信息的角度出发，图2和图3的实验结果表明，捕获到协同过滤信息的矩阵分解算法在进行多轮实验验证的情况下，表现出显著的优势。从实验结果可得，融合矩阵分解模  型无论是在准确率还是召回率上都展示出了较大的优势，产生了更高质量的推荐结果。

3 结语

推荐系统中的传统的协同过滤算法和基于矩阵分解的推荐算法都单独地进行相关推荐，从而导致推荐质量不佳。为解决协同过滤算法与矩阵分解算法中存在的不足，本文提出的融合矩阵分解方法，融合两者优势来解决存在的不足之处，通过Pearson相似度计算每个用户物品的相似项，然后利用相似用户和相似物品增强矩阵分解中的协同过滤信息。大量的实验与理论分析表明，本文所提出的融合推荐算法能够进一步在准确率和召回率上提升推荐性能。融合矩阵分解模型无论是在准确率还是召回率上都有明显的提升，其推荐的结果质量有显著提高。可见，本文提出的融合推荐算法对比原始的方法可以获得更高质量的推荐结果。

参考文献

［1］王梦琪，唐长乐.内容供给侧信息过载问题及优化策略——以互联网内容平台为例［J］.图书情报导刊，2022（9）：30-37.

［2］罗洁，王力.基于用户和项目的协同过滤算法的比较研究［J］.智能计算机与应用，2023（1）：195-197.

［3］张洪为.融合邻域结构信息的概率矩阵分解算法［J］.通化师范学院学报，2022（8）：50-53.

［4］刘超，赵文静，贾毓臻，等.基于改进的BiasSVD和聚类用户最近邻的协同过滤混合推荐算法［J］.计算机应用与软件，2021（5）：288-293.

［5］胡炳文，孙克雷.一种缓解推荐偏好的协同过滤TopN算法［J］.淮南职业技术学院学报，2016（1）：5-9.

（编辑 王雪芬）

Research on matrix factorization recommendation algorithm fusing similar users and items

Hong  Chang， Liu Wei， Lyu  Haochen

（Chongqing Intellectual Property Protection Center， Chongqing 400023， China）

Abstract：  In the recommendation system， the traditional collaborative filtering algorithm and the recommendation algorithm based on matrix factorization are independently recommended， but the independent operation of the two methods has certain shortcomings， resulting in poor recommendation quality. In order to further improve the performance of the recommendation algorithm to improve the recommendation accuracy， we propose a matrix factorization recommendation algorithm that integrates similar users and items. On the basis of the matrix factorization model， combined with the idea of collaborative filtering， the personalized candidate item recommendation of the target user is mined. In this paper， the MoviesLens data set is used to train the model and evaluate its performance. Compared with the original method， the recommendation accuracy is further improved.

Key words： recommendation system; coordinated filtering; matrix factorization