地方高校计算机类学生计算思维的评价探索
康长青 吴中博 朱丽娟 王敏 胡春阳
摘 要:鉴于对高校计算机类学生计算思维能力测评研究不足的现状,形成开展计算思维能力测评的思路。选取抽象建模、算法设计、问题识别与分解、自动化、概括迁移和合作关系六个子能力作为评价指标,基于层次分析法构建了计算思维评价模型。采集核心专业课的期末综合评价数据,经分析得出班级计算思维整体表现和个人计算思维等级,同时阐述了测评结果的应用方向,为新时代计算机类专业人才培养质量的评价提供一种新路径。
关键词:地方高校;计算思维;计算思维测评;评价指标;层次分析法
中图分类号:TP39;G642 文献标识码:A 文章编号:2096-4706(2023)07-0183-04
Abstract: In view of the lack of research on the evaluation of computational thinking ability of computer students in colleges and universities, the idea of developing the evaluation of computational thinking ability is formed. Six sub-capabilities, namely, abstract modeling, algorithm design, problem identification and decomposition, automation, generalization and transfer, and cooperative relationship, are selected as evaluation indicators, and a computational thinking evaluation model is built based on the analytic hierarchy process. Collect the final comprehensive evaluation data of core professional courses, the overall performance of class computational thinking and the level of individual computational thinking are obtained by analysis, and the application direction of the evaluation results is described, providing a new way for the evaluation of the training quality of computer professionals in the new era.
Keywords: local college; computational thinking; computational thinking evaluation; evaluation index; analytic hierarchy process
0 引 言
計算思维是新时代高等学校计算机教育领域的研究热点之一。自从周以真教授在2006年提出计算思维的概念后,计算思维迅速引起国内外计算机科学界和教育界的广泛关注。在我国高等学校计算机教育领域,文献[1]中提出了“计算思维能力的培养”是计算机基础教学的核心任务。文献[2]中提出了计算思维是计算机类专业人才的四大专业基本能力之一。文献[3]中提出“计算机科学中最具基础性和长期性的思想是计算思维”,明确了对学生计算思维的培养在大学计算机基础课程教学中的中心地位。文献[4]中将计算思维2.0定义为“所有领域科学家在应用计算和计算模型进行问题求解时的思维模式,是涵盖所有学科的第三种思维范式”。文献[5]中提出计算思维是从信息运动的角度认知和理解世界的思想和方法,对新工科建设意义重大。文献[6]提出计算思维具有“提升工程计算能力,变革问题求解方式;强化系统设计能力,促进人类行为理解;跨越人才培养鸿沟,塑造专业创新能力”的作用,加强对学生计算思维能力的培养是实现新型工科人才培养目标的关键。总的来说,在以上文献的政策导向和方向指引下,广大计算机教育研究者就计算思维开展了大量的培养内容设计与课程实践模式研究[7-9],而计算思维的能力评测研究则是整个研究工作的核心所在。在国家深化新时代高等教育评价改革的背景下,开展对高等学校计算机类学生计算思维的评价研究,具有十分重大的意义和价值。
1 计算思维的测评现状
计算思维的测评是计算机教育教学的重要诊断环节,更是促进专业教学质量持续改进的重要组成部分,不仅可以用于考查学生的知识技能掌握情况,还可以用于评价教师所授课程的教学质量。国外研究人员已设计出各种各样的计算思维评价工具[9],而国内学界自主研发的计算思维评价工具则非常罕见。由于国内外各个学段的教学目标、教学内容和教学方法有所不同,加上研究者们对计算思维内涵与外延的认知不同,导致各自构建的评价框架和评价方法存有差异。文献[10]构建了由三个一级指标和九个二级指标组成的初中信息技术课程计算思维评价指标体系,采用德尔斐法等方法确定指标的权重值,形成计算思维评分表。文献[11]通过需求调查问卷,总结了职业学校学生所应具备的包含七大能力十七个指标的计算思维能力。北京大学学习科学实验室基于国外的评测系统,设计开发了包含五个维度的线上计算思维等级评测系统。文献[12]针对中小学生从认知和非认知层面将计算思维分解成六个计算思维子能力,实现了计算思维微认证评定。总的来说,现有的计算思维测评研究大多针对K12学段的学生设计评价指标,并基于题目测试成绩和编程测试成绩进行度量和分析[13]。计算机专业是目前普通高等学校的热门专业,每年毕业的学生数量巨大,高校的计算机课程教学体系和初高中的信息技术课程差异巨大,大学生的计算思维该如何测评,是目前非常重要的探索课题。
2 地方高校计算思维测评实践
地方高校计算思维测评是以学生的综合表现作为其进阶依据,刻画学生思维发展的不同层级,具有促进思维向着更精细成熟方向发展的作用,是解决教学、学习和评价一致性的有效手段[14]。由于思维的复杂性,构建计算思维的学习进阶系统需要综合考虑时间跨度的选择、学生学习数据的收集、数据处理模型的构建以及模型结果的分析和应用等因素。
2.1 计算思维测评的总体思路
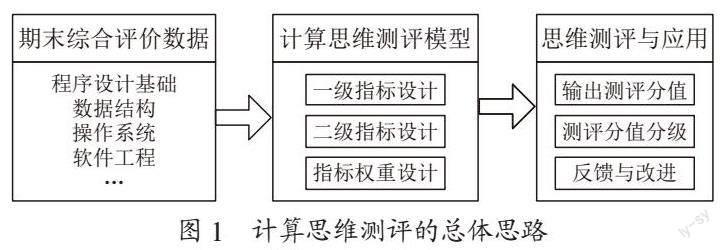
地方本科高校计算机专业(包含计算机科学与技术、软件工程和物联网工程等)的教学目标应建立符合学生学情的计算思维培养和评价方式。所建立的计算思维测评系统应在地方高校应用型人才培养目标和课程实施体系的基础上进行计算思维模型的设计,该模型支持数据的采集和系统目标的实现。因此,我们设计的地方高校计算思维测评系统如图1所示,即通过一二级内涵指标和指标权重的设计,形成计算思维测评模型,通过将现有的期末综合评价数据输入测评模型,得到测评分值并进行思维分级和反馈。
2.2 一级评价指标的设计
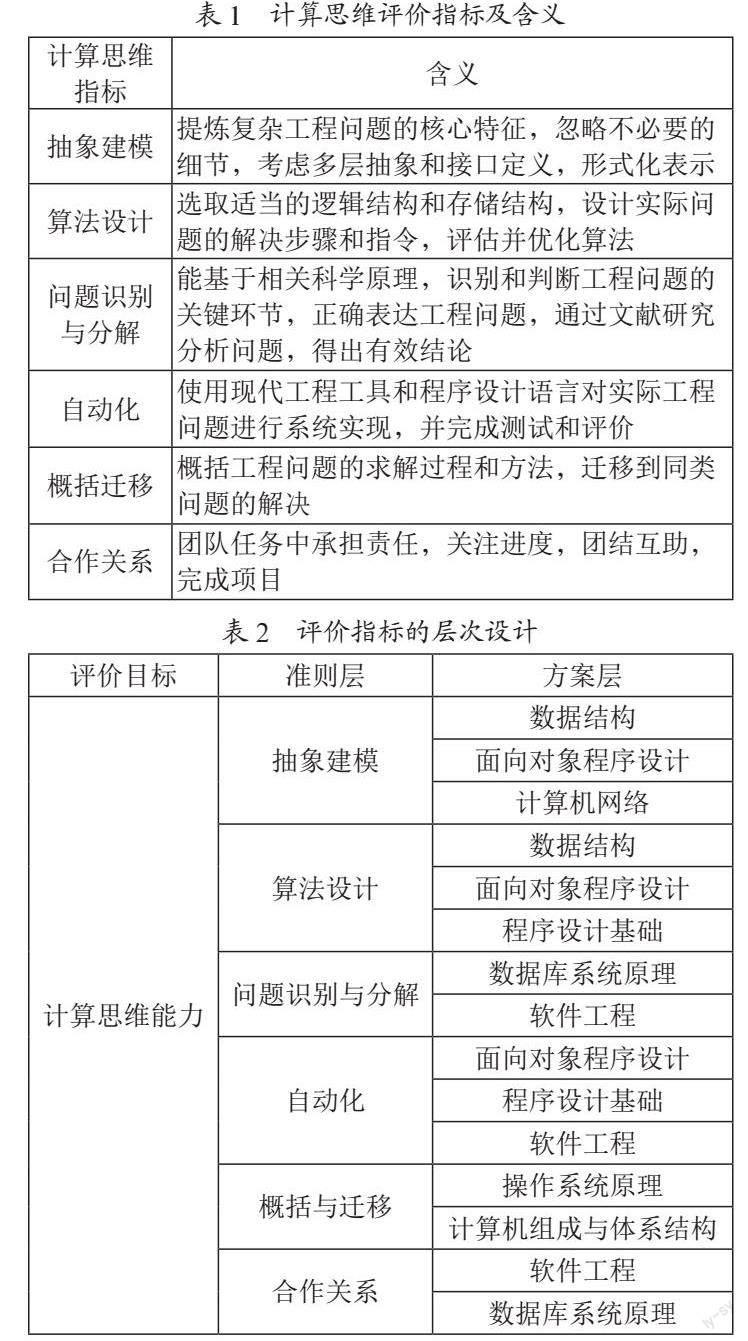
建立面向地方高校计算机类学生的计算思维测评系统,首先要考虑确定适合地方高校人才培养目标的计算思维评价指标。由于国内外研究者对计算思维的内涵与外延并没有达成一致,结合地方计算机专业应用型人才培养目标,综合国内外专家的研究成果,设计计算思维的一级评价指标由抽象建模、算法设计、问题识别与分解、自动化实现、概括迁移以及合作关系六个指标构成,其具体含义如表1所示。
2.3 二級评价指标的设计
通常,计算思维测评是针对每个指标出一套卷子,对学生进行题目测试或编程测试,而现有的大学课程期末综合评价大多融入题目测试、编程成绩、项目绩效等形式,具备融合过程性评价和总结性评价的优点。考虑到测评方式的简单性、可行性,借鉴OBE工程认证的逆向设计思路,将计算思维的指标评价落实到课程培养上,通过课程的综合测评成绩来支撑学生计算思维的达成度计算。因此我们选取计算机类专业的公共核心基础课程,构建计算思维评价指标,如表2所示。
2.4 评价指标权重的计算
计算思维测评模型在确定好一级二级评价指标后还需要进行评价指标权重分配。层次分析法是对实际问题进行定性和定量分析的多属性决策方法,具有简便、实用、灵活的优点[15]。
利用层次分析法构建模型一般分为四步:
1)设计模型的递阶指标体系。
2)构造各层次比较判断矩阵。
3)层次单排序和一致性检验。
4)层次总排序和一致性检验。
利用层次分析法确定计算思维指标权重的具体操作过程如下:
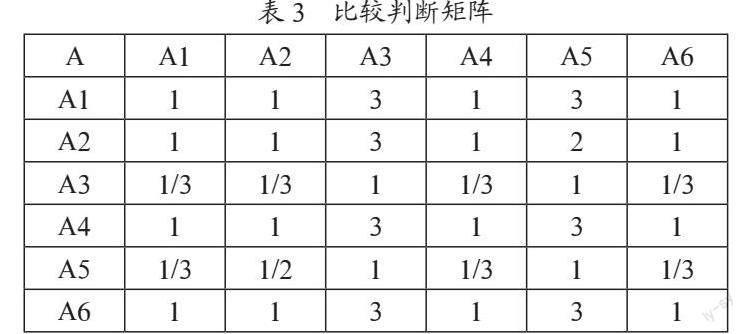
1)在计算思维测评问题层次模型(表2)的基础上,对准则层采用“1—9标度法”,构建比较判断矩阵,如表3所示。
2)选择权重向量的计算方法,计算比较判断矩阵的特征值和特征向量。根据特征向量法AW=λmaxW可以求出该矩阵的最大特征值为6.018 4,该矩阵的特征权向量为W=(0.215 8, 0.203 0, 0.071 9, 0.215 8, 0.215 8)。
3)根据CI=(λmax-n)/(n-1),计算一致性指标。其中λmax为矩阵的最大特征根,n为矩阵阶数,这里最大特征值为6.018 4,矩阵阶数为6,可以算出CI=0.003 7。
4)利用公式CR=CI/RI,计算一致性比例,进行一致性检验。其中CI为(3)中的一致性指标,RI为平均随机一致性指标,当n=6时,RI=1.24,因此可以算出CR=0.003<0.1,表明比较判断矩阵(表3)的设计通过了一致性检验,无须修正。
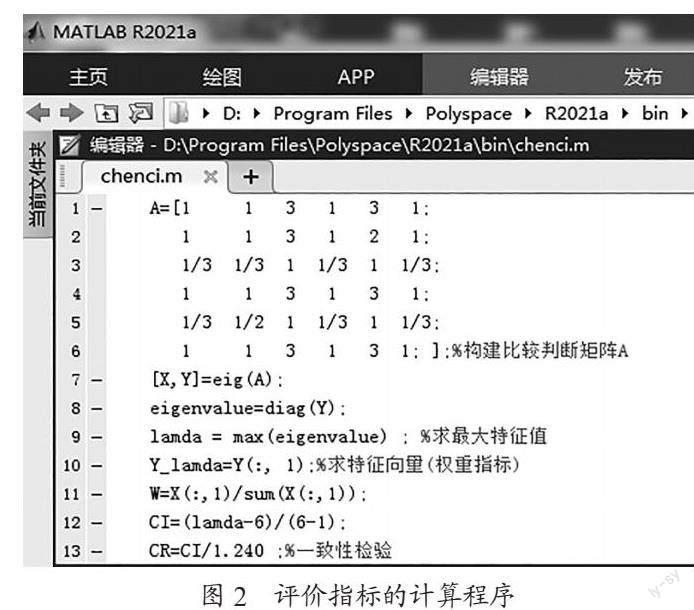
上面的整个计算过程可以采用MATLAB编程软件进行编程实现,图2给出了评价指标的计算程序。同理,针对准则层的各个指标,在方案层继续采用上面的方法,可以求出每个方案指标的权重,因此计算思维测评模型构建完成。
2.5 计算思维测评与应用
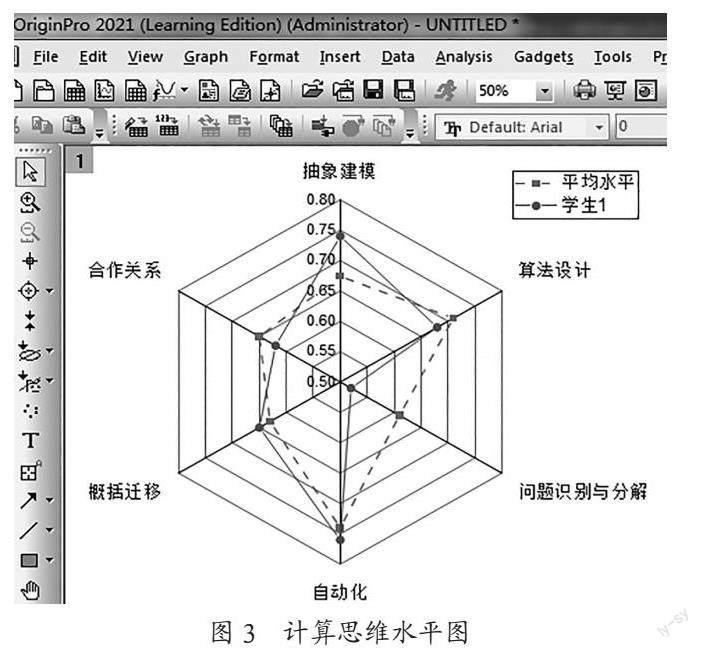
利用湖北文理学院物联网工程1911班8门核心专业课的期末综合评价成绩(包含平时作业、实验成绩、项目成绩、期末考试成绩等)来验证所建计算思维测评模型的效果。通过模型测评,可以得到全班的平均计算思维水平和某学生的计算思维水平,利用Origin画图软件画出雷达图,如图3所示。从中可以看出全班的平均抽象建模能力为0.67,平均算法设计能力为0.71,平均问题识别与分解能力为0.61,平均自动化能力为0.63,平均概括迁移能力为0.63,平均合作关系能力为0.65,因此可以得到全班计算思维能力为0.682。将计算思维分为三个等级:小于0.6为不合格,介于0.6和0.8之间为合格,大于0.8为优秀。
班级和专业的计算思维测评数据可在一定程度上反映学生整体的计算思维水平,可以辅助教师进行课程教学的反思和改进,教师可以依据测评数据分析学生的学习风格和学习能力,调整课堂教学设计和教学策略,开展差异化教学,持续优化教学方案,不断提高教学质量。学生的计算思维能力数据刻画了学生专业学习后的思维发展情况,有助于学生进行自我反思,深挖自身潜力,促进学生深层次的认知与自我评价,提升学生的计算思维能力。
3 结 论
新时代高等教育评价应该加快推进高等教育评价技术和方法的研究,不断完善基于多元主体的高等教育评价体系。本论文利用层次法分析框架,设计了地方高校计算机类学生的计算思维测评模型,呈现了学生学完8门核心专业课后的计算思维水平,丰富了地方高校应用型人才培养的评价体系,具有一定的借鉴和参考价值。计算思维作为计算机科学领域最具有基础性和长期性的思想,需要更多的计算机专业教师在课程教学中开展以培养学生计算思维为目标的课程教学改革,不断进行计算思维相关理论的研究和应用探索,共同推进我国计算思维教育的长远发展。
参考文献:
[1] 何钦铭,陆汉权,冯博琴.计算机基础教学的核心任务是计算思维能力的培养——《九校联盟(C9)计算机基础教学发展战略联合声明》解读 [J].中国大学教学,2010(9):5-9.
[2] 蒋宗礼.计算机类专业人才专业能力构成与培养 [J].中国大学教学,2011(10):11-14.
[3] 余大品.计算思维教学改革宣言 [J].中国大学教学,2013(7):7-10+17.
[4] 陈国良,李廉,董荣胜.走向计算思维2.0 [J].中国大学教学,2020(4):24-30.
[5] 狄长艳,周庆国,李廉.新工科背景下對于计算思维的再认识 [J].中国大学教学,2019(Z1):47-53.
[6] 邓磊,战德臣,姜学锋.新工科教育中计算思维能力培养的价值探索与实践 [J].高等工程教育研究,2020(2):49-53.
[7] 刘敏娜,张倩苇.国外计算思维教育研究进展 [J].开放教育研究,2018,24(1):41-53.
[8] 阳小华,刘志明,刘杰,等.我国计算思维教学的回顾与展望 [J].现代远距离教育,2018(2):3-11.
[9] 朱珂,徐紫娟,陈婉旖.国际视阈下计算思维评价研究的理论和实践 [J].电化教育研究,2020,41(12):20-27.
[10] 聂永苹.初中信息技术课程计算思维评价指标构建研究 [D].曲阜:曲阜师范大学,2018.
[11] 张兆芹,陈守芳,贾维辰,等.职业教育中学生计算思维能力的培养方案探析 [J].职教论坛,2016(3):14-19.
[12] 郁晓华,王美玲,程佳敏,等.计算思维评价的新途径:微认证 [J].开放教育研究,2022,28(1):107-120.
[13] 郁晓华,王美玲.计算思维培养之路还有多远?——基于计算思维测评视角 [J].开放教育研究,2020,26(1):60-71.
[14] 王磊,黄鸣春.科学教育的新兴研究领域:学习进阶研究 [J].课程.教材.教法,2014,34(1):112-118.
[15] 邓雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究 [J].数学的实践与认识,2012,42(7):93-100.
作者简介:康长青(1979—),男,汉族,湖北襄阳人,副教授,博士,主要研究方向:程序设计课程教育、计算机视觉;通讯作者:胡春阳(1975—),男,汉族,湖北襄阳人,副教授,博士,主要研究方向:大数据处理和云计算。

