基于IAO 优化HKELM 的空气质量指数预测

周 韦， 孙宪坤， 万俊杰

（上海工程技术大学， 电子电气工程学院， 上海 201620）

0 引 言

城市环境污染不仅影响社会经济的发展，对人们的身体也会造成有害的影响。 据统计，中国空气污染区域占国土面积的1／4，受影响的人口近7 亿。因此实现对空气质量指数（AQI）进行准确有效地预测成为重中之重。

目前，国内外空气质量预测模型主要有回归统计分析模型、时间序列模型、灰色理论模型等。 但是AQI 数据是混沌的、非平稳的，导致上述模型的预测精度不高。 神经网络模型具有良好的学习能力，受到广大学者的关注。 文献［1］ 将 BP （Back Propagation）神经网络应用到了空气质量预测中，取得了良好的预测效果；文献［2］ 提出了一种RBF（Radial Basis Function）神经网络空气质量预测模型，相比BP 神经网络，效果有所提升。 然而神经网络具有学习速度慢，易陷入局部极值等缺陷。

文献［3］提出极限学习机（ELM），是一种前馈神经网络，具有学习速度快、泛化能力强等优点；文献［4］ 提出了一种 PSO （ Particle Swarm Optimization）－ELM 的空气质量预测模型，该模型可以有效提高空气质量预测精度；文献［5］提出了一种基于IPSO（Improved Particle Swarm Optimization）－ELM 的空气质量预测模型，相比传统的基于BP 和ELM 的神经网络模型，该模型具有更高的精度。 但是ELM 也存在一些缺点，比如网络的隐层节点个数难以确定、不同的参数对预测结果有不同的影响等。因此文献［3］又引入了支持向量机中的核函数，使得极限学习机无需设置隐藏层神经元个数和输入权值参数，解决了ELM 过拟合和易陷入局部极值的问题。

为了进一步提高空气质量预测模型的预测精度，本文提出了一种基于IAO 优化混合核极限学习机（HKELM）的空气质量指数预测模型。 首先，为提高天鹰优化器（AO）的寻优能力，引入改进的混沌初始化策略和自适应t 分布策略对其进行改进，得到改进的天鹰优化器（IAO）；其次，结合径向基核函数和多项式核函数构造具有更强泛化能力的混合核极限学习机模型，利用IAO 算法来优化HKELM 模型的参数；最后，将IAO－HKELM 模型应用于实际案例中，并与其他模型的预测结果及误差进行对比。 结果表明，本文所设计模型具有更高的稳定性和预测精度。

1 混合核极限学习机

极限学习机（ELM）作为一种新型单隐藏层的前馈神经网络模型，具有学习能力快，泛化能力强等优点，在处理非线性回归方面具有良好的效果［6］。假设有D个训练样本｛（xi，yi），i＝1，2，…，D｝，ELM输回归模型可以表示为式（1）：

其中，x表示输入数据向量；f（x） 表示网络输出；h（x） 和H表示隐藏层映射产生的矩阵；β表示隐藏层与输出层之间的权值。

为使模型具有更好的泛化能力，引入对角矩阵I0和惩罚系数C，然后根据广义逆矩阵原理可得式（2）：

其中，y＝［y1，y2，…，yD］ 为期望输出。

为了进一步增加模型的稳定性，文献［3］引入核方法， KELM （Kernel Based Extreme Learning Machine）的核矩阵表示为式（3）：

KELM 用核矩阵ΩKELM代替了ELM 中HHT，并通过核函数将输入样本映射到高维隐层特征空间中，可得式（4）：

其中，K（xi，xj） 为核函数。

常见的核函数主要有以下4 种：

（1）高斯核函数，式（5）：

（2）多项式核函数，式（6）：

（3）线性核函数，式（7）：

（4）感知器核函数，式（8）：

其中，σ、m、n和d为混合核参数，λ为多项式核函数的权系数。

KELM 的性能由核函数决定［7］。 本文结合了多项式核函数和高斯核函数作为KELM 的核函数，以提高模型的性能。 多项式核函数是一种全局核函数，拥有较差的局部学习能力，多项式核函数曲线如图1 所示，其中测试点X＝0.5，m＝1，n＝1，d取1、2、3 和4，由图1 可以看出多项式核函数的全局特性体现在与测试点相距较远的点影响较大。

图1 多项式核函数曲线Fig. 1 Polynomial kernel function curve

高斯核函数是一种局部核函数，具有很好的局部学习能力，但是对超出一定范围的样本无法进行准确有效地预测，高斯核函数曲线如图2 所示，其中测试点X＝0.5，σ取0.1、0.2、0.3 和0.4。 由图2 可以看出高斯核函数的局部特性体现在与测试点相距较近的点影响较大。

图2 高斯核函数曲线Fig. 2 Gaussian kernel function curve

混合核函数可以同时兼顾两者的优点，将两种核函数进行线性组合，形成混合核函数，式（9）：

混合核函数曲线如图3 所示，其中测试点X＝0.5，λ取0.1，0.2，0.3 和0.4，高斯核函数中σ取0.1，多项式核函数中m＝1，n＝1，d＝2。 由图3 可以看出，混合核函数不仅对测试点周围的样本点有影响，而且对距离测试点有一定距离的样本点也有一定影响，因此混合核函数有效结合了高斯核函数和多项式核函数的优点，弥补了单一核函数的不足。

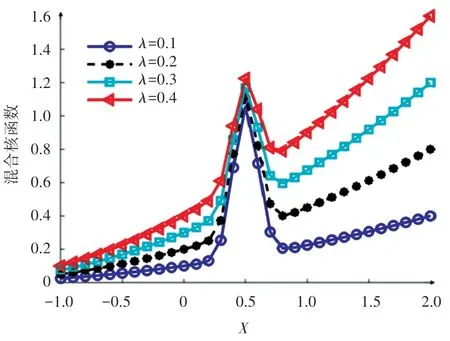
图3 混合核函数曲线Fig. 3 Mixed kernel function curve

训练混合核极限学习机（HKELM）时采用改进的麻雀搜索算法对参数σ、m、n、λ以及惩罚系数C进行优化。

混合核极限学习机（HKELM）通过混合核函数将输入样本映射到高维的隐层特征空间中，用核映射代替了极限学习机中的随机映射，增强了模型的学习能力和泛化能力，其拟合能力优于非核的极限学习机［8］。 基于以上优点，本文采用HKELM 实现空气质量指数预测。

2 天鹰优化器及其改进

2.1 天鹰优化器

AO 是一种新型智能优化算法，该算法用数学模型模仿了天鹰在狩猎过程中的行为［9］。 AO 算法包括两个阶段，分别为探索阶段和开发阶段。当k≤（2／3）∗K，k为当前迭代次数，K为总迭代次数，执行探索阶段，否则执行开发阶段。 探索阶段又分为扩展探索和缩小范围探索；开发阶段又分为扩大开发和缩小范围开发。

首先，AO 算法利用式（10）来确定N个个体的初始值。

其中，rand为［0，1］之间的随机数，i＝1，2，…，N，j＝1，2，…，d；N表示种群数量；d表示维数；UBj和LBj分别表示维度为j的上限和下限。

2.1.1 扩展探索

天鹰在高空翱翔，确定探索空间区域，猎物在哪里，用公式（11）表示其行为：

其中，K表示最大迭代次数；Xbest（k） 表示当前最佳位置；XM（k） 表示在第k次迭代中个体位置的平均值；rand为0～1 之间的随机数。

XM（k） 计算公式为（12）：

其中，d表示优化变量的维度。

2.1.2 缩小范围探索

当天鹰发现猎物区域，在目标猎物上方盘旋，缩小猎物所在区域，准备进攻。 用公式（13）表示其行为：

飞行分布函数Levy（d） 如式（14） 所示：

其中，s＝0.01，β＝1.5，u和v为［0，1］之间的随机数。

螺旋形状y和x如式（15） 所示：

其中：

r1为［0，20］ 之间的随机数，d1表示1 到d之间的正整数，U＝0.005 65，ω＝0.005。

2.1.3 扩大开发

当猎物区域被精准确定，天鹰垂直下降进行初步攻击。 用公式（19）表示其行为：

其中，rand∊［0，1］，α＝0.1，δ＝0.1。UB和LB分别表示搜索空间的上界和下界。

2.1.4 缩小范围开发

象鼩(qú)，又名跳鼩，是原产于非洲的小型哺乳动物。之所以被称为象鼩，是因为它们的长鼻子让人联想到大象，而它们的身形样貌又和鼩鼱类似。不过，科学家经过分析得出，象鼩和鼩鼱是两类不同的动物，而小小的象鼩与大象的亲缘关系反而更近。

当天鹰接近猎物时，根据猎物的随机运动在陆地上攻击猎物。 用公式（20）表示其行为：

其中，QF是用于平衡搜索策略的质量函数，使用式（21）进行计算；G1表示猎食动物在猎食过程中用于追踪猎物的各种动作，使用式（22） 进行计算；G2表示从2～0 的递减值，使用式（23）进行计算。

2.2 改进天鹰优化器

AO 与其他群智能优化算法相比，不仅寻优精度高，而且收敛速度快。 然而，AO 同其他群智能算法一样，在迭代后期会出现种群多样性减少，易陷入局部最优等问题。 本文提出了一种改进的AO，首先，利用Tent 混沌映射初始化种群，提高算法的全局搜索能力；其次，引入自适应t 分布变异更新其位置，有效改善算法易陷入局部极值的缺陷。

改进策略如下：

2.2.1 Tent 混沌映射

AO 采用随机生成的方式对种群初始化，会导致天鹰种群分布不均匀。 而混沌映射具有规律性，遍历性等特点，因此本文采用混沌序列对天鹰的位置进行初始化。 Tent 映射分布直方图如图4（a）所示，可以看出Tent 映射分布较为均匀，张娜等人［10］指出Tent 混沌序列在迭代时存在陷入小周期点和不稳定周期点的问题，因此在Tent 混沌映射表达式中加入了随机变量rand（0，1）×（1／NT），改进后的Tent 混沌序列分布图如图4（b）所示，表达式（24）如下：

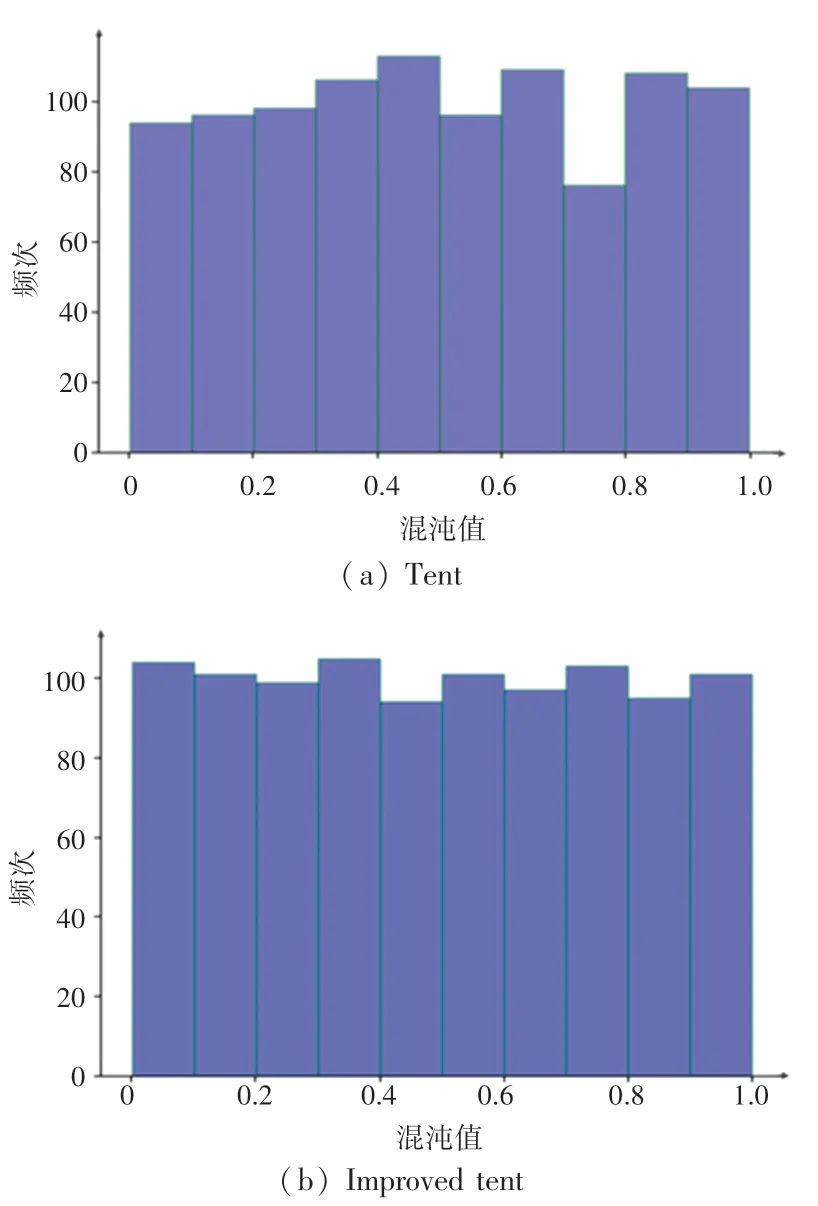
图4 不同混沌序列分布直方图Fig. 4 Distribution histogram of different chaotic sequences

经过贝努利变换后的表达式（25）如下：

其中，NT表示混沌序列中粒子的数量，rand（0，1） 是［0，1］ 之间的随机数。

本文采用改进的Tent 混沌映射来初始化种群，使得初始种群的位置分布更均匀。 步骤如下：

（1）产生（0，1）之间的随机数x0，即i＝0；

（2）根据式（25）进行迭代计算，产生一个X序列，i自增1；

（3）当i到达最大迭代次数时，保存好X序列；

（4）将X序列的元素按照式（26）映射到天鹰个体上，得到xnewi；

其中，UB和LB分别表示搜索空间的上下界。

2.2.2 自适应t 分布策略

t 分布又称学生分布，其分布函数曲线形态由参数自由度的值n决定。 t 分布、高斯分布和柯西分布图如图5 所示，当自由度n越小，曲线的形态越平坦；当自由度n＝1 时，t 分布为柯西分布，即t（n＝1） →C（0，1）；当自由度n越大时，曲线形态表现越高耸，曲线类似于标准正态分布曲线；当自由度n无限大时，t 分布为高斯分布，即t（n＝∞）→N（0，1）。

图5 t 分布、高斯分布和柯西分布函数分布图Fig. 5 t distribution， Gaussian distribution and Cauchy distribution function

对天鹰位置利用自适应t 分布进行更新，xti表示经过t 变异后的天鹰的位置。 式（27）：

其中，xi为第i个鹰个体的位置，t（k） 表明选择当前迭代次数为参数自由度的t 分布。

当前期迭代次数k较小时，t 分布类似柯西分布变异，此时的t 分布算子取得较大值，位置变异的步长较大，使得算法拥有较好的全局搜索能力；在迭代中期，t 分布由柯西分布变异向高斯分布变异转变，t分布算子取值相对折中，使得算法结合了两者的优势，同时兼顾全局和局部搜索能力；当后期迭代次数k较大时，t 分布类似高斯分布变异，此时的t 分布算子取得较小值，变异步长较小，使得算法拥有较好的局部搜索能力，该策略有利于算法找到全局最佳点。

2.3 IAO 性能评估

为验证IAO 算法的性能，本文使用了PSO（Particle Swarm Optimization）算法、GWO（Grey Wolf Optimizer）算法、AO 算法和IAO 算法对测试函数进行仿真实验，各算法参数设置见表1。 每个算法的种群规模为30，最大迭代次数为1 000。 测试函数选取了多维单峰函数Sphere 和多维多峰函数Ackley，函数维度为50。 各算法独立运行20 次，得到的测试函数优化曲线如图6 和图7 所示，适应度值为测试函数值。

表1 参数设置表Tab. 1 Parameter settings

图6 Sphere 函数优化曲线Fig. 6 Sphere function optimization curve

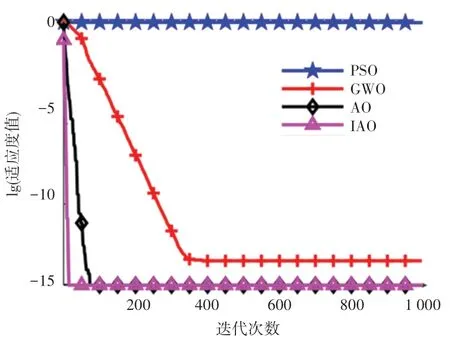
图7 Griewank 函数优化曲线Fig. 7 Griewank function optimization curve

从图6 可以看出，单峰Sphere 函数在PSO、GWO 和AO 在寻优的过程中早早就陷入局部极值且无法自拔，导致算法收敛性能较弱。 而IAO 相比其他算法不仅寻优精度高，而且具有更快的收敛速度。 从图7 可以看出，IAO 在相同的迭代次数中其多峰Griewank 函数能够寻找到更优的值，而且在寻优精度和收敛速度上IAO 总是优于其他算法，曲线先出现拐点表明收敛速度快，适应度值越低表明寻优精度越高。

3 基于IAO－HKELM 的空气质量指数预测

HKELM 模型的预测精度由混合核参数σ，m，n，λ以及惩罚系数C决定，因此参数的优化尤为重要。 本文采用改进的天鹰优化器来对5 个参数寻优，从而达到最佳的预测效果。

（1）数据集划分。 将空气质量样本数据划分为训练集与测试集，并作归一化处理。

（2）初始化参数。 设置参数σ、m、n、λ和C的优化区间UB，LB，以及IAO 算法的相关参数值，利用式（26） （27）混沌映射初始化麻雀种群。

（3）选择适应度函数，将训练样本的预测值和真实值yi的均方误差（MSE） 作为天鹰个体的适应度值，由式（13）计算可得。

（4）计算天鹰个体的适应度值，根据适应度值确定当前最佳Xbest（k），更新XM（k），G1，G2，Levy（d） 等。

（5）当k≤（2／3）∗K时，且rand≤0.5 时，利用式（11）更新天鹰个体的位置，否则根据式（13）更新天鹰个体的位置。

（6）当（2／3） ∗K≤k≤K时，且rand≤0.5 时，利用式（19）更新天鹰个体的位置，否则根据式（20）更新天鹰个体的位置。

（7）根据式（27）对天鹰位置进行t 分布变异扰动。

（8）计算每只天鹰进行t 分布后的适应度值，将经过t 分布操作后的新解适应度值与原值进行比较，更新全局最优信息。

（9）终止条件。 若已达到最大迭代次数K时，则输出最优天鹰个体位置对应的参数（C，λ，q，σ2），并建立混合核IAO－HKELM 空气质量指数预测模型。 否则返回步骤5。

（10）利用建立好的混合核IAO－LSSVM 模型进行空气质量指数预测。

为比较各模型性能，选用均方根误差（RMSE），平均绝对误差百分比（MAPE） 和平均绝对误差（MAE） 这3 个指标作为模型的评价指标。 各指标的计算公式分别如式（28）～（30） 所示。

其中，表示预测值；Yi表示真实值；S为测试数据样本总数。

4 案例分析

4.1 数据来源

实 验 中 通 过 天 气 后 报 数 据 网 站（http：／ ／www.tianqihoubao.com／） 收集郑州市2017年～2019 年750 组天气数据，部分数据见表2。 选择其中650 组数据作为训练样本，剩余100 组数据作为测试样本，其中AQI 为模型输出，NO2、O3、CO、PM2.5、PM10、SO2为模型输入。

表2 部分实验数据Tab. 2 Part of experimental data

4.2 模型参数确定

为了验证IAO－HKELM 模型的预测精度，选取了KELM、HKELM、PSO－HKELM、GWO－HKELM、AO－HKELM 和IAO－HKELM 模型，在相同的测试集上比较模型的精度。 各优化算法参数设置与IAO性能测试相同，维度d＝5，K＝100。 KELM 模型选择单一高斯核函数，参数σ＝10，C＝10；HKELM 模型选用高斯核函数和多项式核函数结合的混合核函数，参数λ＝0.5，σ＝10，m＝1，n＝1，C＝10；其余模型中参数λ∈［0，1］； 剩余参数取值下界为［0.01，0.01，0.01，0.01］，上界为［100，100，100，100］。各优化算法优化HKELM 得到的模型参数见表3 ，各模型预测结果如图8 所示。

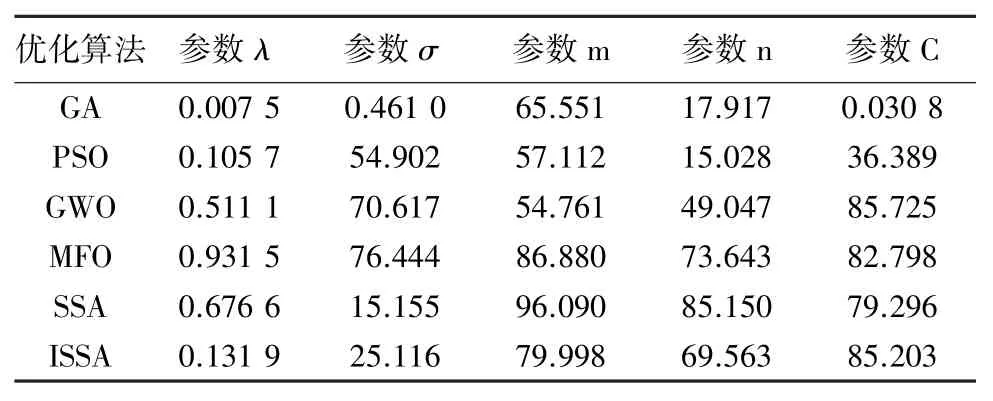
表3 HKELM 模型参数Tab. 3 HKELM model parameters

图8 各模型的预测结果Fig. 8 Prediction results of different model

从图8 可以看出，IAO－HKELM 模型对于预测样本的预测精度上优于其他模型。 各模型预测值与真实值的误差见表4，选择3 个评价指标中的均方根误差（RMSE） 来比较这几个模型的性能，其中采用单一核函数的KELM 模型误差较大为4.281 9，混合核函数HKELM 模型相比KELM 误差有所减少为2.963 7，但是相比采用优化算法优化后的模型，还存在一定误差。 PSO－HKELM、GWO－HKELM 和AO－HKELM模型的均方根误差分别为2.963 7、2.640 7和2.145 6，而ISSA－HKELM 模型的均方误差为1.771 2，误差最小，说明IAO－HKELM 预测模型对于空气质量指数预测取得了很好的效果，相比其余几个常用模型，误差更小，精确度更高。

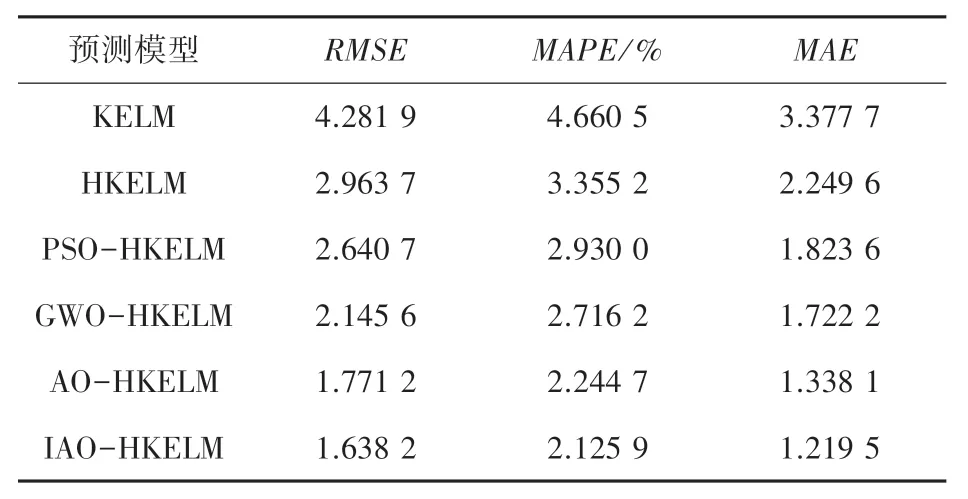
表4 误差对比表Tab. 4 Error comparison

5 结束语

本文提出一种基于改进天鹰优化器优化混合核极限学习机的空气质量指数预测模型。 通过引入改进的混沌初始化策略和自适应t 分布策略对天鹰优化器进行改进；结合径向基核函数和多项式核函数构造具有更强泛化能力的混合核极限学习机模型，最终得到了IAO－HKELM 预测模型。 同过与其他模型进行实验对比，最终验证了该模型预测精准度更高，稳定性更强，满足实际的应用。